基于递归定量分析的生理信号情感识别
李才隆,叶 宁,2,黄海平,2,王汝传,2
(1.南京邮电大学 计算机学院、软件学院、网络空间安全学院,江苏 南京 210000; 2.南京邮电大学 江苏省无线传感网高技术重点实验室,江苏 南京 210000)
1 概 述
随着科技的发展,人们已经离不开因特网,计算机的发展给社会带来了巨大的经济价值,人与计算机的交互时间越来越长。人们迫于生活、学习等方面的压力,心理的压力与焦虑也越来越多。因此,使用机器检测人体的情感状态并辅助人们调整心理状态已经变得越来越有价值。目前,国内对情感在语音情感理解、文本情感理解等方面的研究获得了很大成果。文献[1]通过聚合经验模态分解算法以非线性的处理方式提取语音信号特征,情感识别率达到91.67%。文献[2]使用基于深度学习的卷积神经网络模型分析文本的情感倾向,采用分段池化的策略将句子结构考虑进来,实验结果表明较基线模型都有显著的提升。文献[3]以语音信号和面部表情信号为研究对象,提出了将提取的语音信号和面部表情信号特征进行融合的多模式情感识别算法,使整个情感信息的融合过程更加接近人类情感识别,情感识别率达91.2%。
与语音情感识别、文本情感识别等相比,关于生理信号的情感识别已成为一个非常重要的研究方向。这是因为人体的生理信号与人体密切相关,生理信号被认为是测定情感状态的客观指标之一,它们可以更直接反映出人体情感状态。当今技术的发展使得生理信息不再是侵入型的。随着可穿戴设备的发展,微型化的传感器产品已经广泛应用于人们的日常生活,例如智能手表、智能手环等等。它们通过与人体的接触,很容易并且很方便就可以获取人体的相关生理信号数据,并且这个过程不会对用户造成明显的干扰。随着科技的发展,基于生理信号的情感识别设备必将改变人们的日常生活,在享受着机器带给人们经济效益的同时,又可以享受机器带给人们精神上的享受。
目前基于生理信号的情感识别特征提取研究大多集中于时域和频域的统计特征。现今有大量实验证明,非线性特征作用极大。混沌理论在1985年首次应用于脑电非线性动力学分析[4]。Natarajan等对不同精神状态下的脑电信号进行采集,提取了脑电信号的多个非线性特征,如近似熵、Hurst指数和关联维数等。结果显示主体联想维度中的认知活动将显著增加[5]。Eero Vayrynen等在语音信号中研究了个体悲伤、愤怒、喜悦、中性等情绪,提取了语音信号中的非线性特性,使用非线性特性提取方法对个体情绪进行识别[6]。E D Beyli提取了人体心跳信号的小波系数和李雅普诺夫指数等非线性特征,使用神经网络等方法构建模型,达到了对心脏病进行早期检测的目的[7]。文献[8]采用多种非线性数据值分析方法提取情感生理信号的非线性特征,发现了非线性特征提取对情感分类效果显著。文献[9]对皮层脑电时间序列进行相空间重构以及非线性特征提取,实验结果表明非线性特征的提取对预报癫痫发作和治疗有一定的帮助。文献[10]通过对脑卒中后抑郁症患者脑电信号的非线性动力学特征进行分析,发现脑卒中后抑郁症患者的脑电信号样本熵和LZC复杂度值均小于健康人。文献[11]对运动诱发局部肌肉疲劳肌音信号进行非线性特性分析,其结果表明计算混沌的特征指数可以对肌肉运动特征进行分类分析。
递归图特征就是非线性特征中的一种。在研究人体生理信号的基础上,文中提出了基于递归图和递归定量分析相结合的方法,提取了生理信号中基于递归定量分析的10组特征:递归率(recurrence rate)、确定率(determinism)、平均的对角线长度(averaged diagonal length)、最长对角线长度(length of longest diagonal line)、对角线长度熵(entropy of diagonal length)、构成垂直/水平线的递归点百分比(laminarity)、捕获时间(trapping time)、最长垂直线长度(length of longest vertical line)、第一型递归时间(recurrence time of 1st type)、第二型递归时间(recurrence time of 2nd type),并与德国Augsburg大学提取的传统统计特征在情感识别效果上进行对比。最后采用神经网络、K近邻、朴素贝叶斯、决策树算法进行情感识别。
2 递归图理论
在自然生活中存在着很多反复性行为,例如周期性(如季节更替),还有不规则的周期性(如厄尔尼诺南方涛动)。根据庞加莱复发定理,某些系统经过足够长的有限时间回到初始状态时非常接近。也就是说,状态的再次发生,意味着状态在一段时间里又是任意接近的,这是确定性动力系统的基本特征,对于非线性系统或者混沌系统具有典型的特征。这些在自然界中的重现现象已经为人们所知,并在很早就有人进行了相关的研究工作。
自然界中存在着相当多的非线性混沌特征信号,生物体的电信号就属于这类典型。现如今,在人体的生理信号(例如脑电信号、心电信号、皮肤电信号、肌电信号)中挖掘有效信息,进而分类人体的健康状态,已成为医学中不可逾越的一个问题。生理信号是一种非线性时间序列信号。与周期性信号相比,非线性时间序列信号的运动状态不可能像周期性信号那样回到之前的某个状态,这就给研究生理信号工作带来了极大的挑战。但是,由于这种非周期性信号具有伪随机性,其运动状态可能接近之前某个时间的运动状态,也就是说,在某两个时刻,这种非周期信号具有相似的动力学行为。递归图就是一种可以分析时间序列周期性以及非平稳性的重要方法,揭示了时间序列的内部结构,并给出有关相似性、信息量和预测性的先验知识,可以检验时间序列的平稳性、内在相似性。
递归图由Eckmann等[12]于1987年提出,主要用于对非线性动力系统的定性分析。递归图的数学定义如下:
Ri,j=Θ(εi-||xi-xj||),xi∈Rm,
i,j=1,2,…,N
(1)
递归图可以用来描述这种两状态间的相互靠近程度及靠近程度的频率[13]。其实质就是将高维运动状态的轨迹映射到二维图形中,从而可以直观地看出其动力学行为。从图形上看,递归图是一个0和1构成的二维矩阵。矩阵值是高维运动状态中两个位置的运动状态间的距离,选取一个阈值,若两个位置的运动状态间的距离大于这个阈值,则值为1,反之为0。
求递归图首先要进行相空间重构。对于非线性时间序列信号一般采用延迟坐标状态空间重构法。给定时间序列{x(1),x(2),…,x(n)}的不同时间延迟0,τ,…,(m-1)τ,构造m维相空间矢量:
Xi(t)={x(t+i),x(t+i+τ),…,x(t+i+(m-1)τ)},i=0,1,…,m-1
(2)
其中,m是嵌入维数,τ是时间延迟。
然后求两个状态之间的距离,选择合适的距离阈值,求两个时刻的递归状态值。根据两个时刻的递归状态值,以i时刻为横坐标,j时刻为纵坐标,可以得出一个0和1两个值的递归矩阵R。根据递归矩阵画一个黑白二色矩阵为递归图,当两个位置的运动状态间的距离大于选取的阈值时,即Rij=1时,递归图上为黑点,当两个位置的运动状态间的距离小于选取的阈值时,即Rij=0时,递归图上为白点。图1是一段皮肤电信号的递归图。

图1 皮肤电信号递归图
3 参数提取
3.1 非线性特征提取
递归图在非周期信号中结构比较复杂,难以得到较为准确的信息。为了更好地对递归图进行定量分析,Zbilut等[14]提出了递归定量分析(recurrence quantification analysis,RQA)方法。主要目的是将图形量化,使用一些量化指标可以更好地得到这些非周期信号的一些特征。在递归图中提取如下的量化指标:
(1)递归率(recurrence rate):指递归图中递归点的密度,就是递归点的百分比(在递归图中黑色点总数的比例)。
(3)
(2)确定率(determinism):指递归图中一小部分形成对角线的递归点的百分比(构成平行对角线方向的线段上黑点所占比例)。
(4)
其中,lmin为最小的对角线长度;P(l)为长度为l的对角线比例。
(3)对角线长度的平均值(mean diagonal line length):平行于对角线方向线段的加权平均值。
(5)
(4)熵(entropy):主要衡量递归结构的复杂性。
(6)
(5)构成垂直/水平线的递归点百分比(laminarity):构成垂直/水平直线的递归点比例。
(7)
其中,P(v)为递归图中长度为v的垂直线比例。
(6)捕获时间(trapping time):指垂直线的平均长度。
(8)
(7)最长垂直线长度(longest vertical line)。
Vmax=max({vi;i=1,2,…,Nv})
(9)
(8)最长对角线长度(longest diagonal line)。
Lmax=max({li;i=1,2,…,Nl})
(10)
(9)第一型递归时间(recurrence time of 1st type)。
T1(i)=ti+1-ti,i=1,2,…,K
(11)
(10)第二型递归时间(recurrence time of 2nd type)。
T2(i)=ti+1-ti,i=1,2,…,K
(12)
3.2 统计特征提取
为了与传统统计特征情感识别性能进行对比,计算了德国Augsburg大学在皮肤电信号、肌电信号、呼吸信号中提取的常见统计特征,包括平均值、中位数、标准差、最大值、最小值、最小值比率、最大值比率、一阶差分的均值、一阶差分的中位数、一阶差分的标准差、一阶差分的最大值、一阶差分的最小值、一阶差分的最小值比率、一阶差分的最大值比率、二阶差分的均值、二阶差分的中位数、二阶差分的标准差、二阶差分的最大值、二阶差分的最小值、二阶差分的最小值比率、二阶差分的最大值比率这21个特征。
4 实验与结果分析
4.1 数据获取
实验选取了德国Augsburg大学提供的生理信号数据库,该数据库是由一个歌唱家处于4种不同基调的歌曲诱发下产生的四种情感(joy、anger、sadness、pleasure)信号组成[15]。分别在每一种情感状态下采集了2分钟的4种生理信号,主要使用其中的皮肤电信号、肌电信号、呼吸信号。它们的采样频率都为32 Hz,持续25天的数据采集,共100个样本。每组信号的原始数据长度都为3 840。图2所示为一段原始的生理信号,自上而下分别是皮肤电信号、肌电信号和呼吸信号。
4.2 数据处理
由于生理信号的频率较低,一般皮肤电信号的有效频率在0.3 Hz以下。为此,采用低通滤波器对生理信号进行预处理,并且皮肤电信号中有基线漂移噪声,为此,实验中去除了皮肤电的基线漂移。对于肌电信号,使用低通滤波器获取0.4 Hz以下的有效部分。呼吸信号获取0.5 Hz以下的有效部分。图3是经过处理后的生理信号图。
4.3 特征提取与分类识别
使用第3节中的参数提取方法,提取了生理信号中的非线性特征和常规统计特征。使用常用的分类识别算法,将这些算法进行目标情感的分类识别。
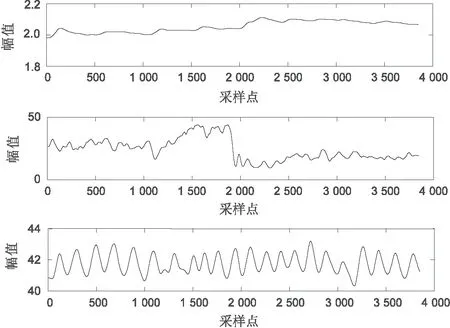
图3 处理后的生理信号
为降低复杂性,采取二分类情感识别的特征选择模型,即假设一种情感是目标情感,其他的则认为是干扰的情感[16]。采用正确率(TPR)和错误率(FPR)来评估分类器的分类性能,公式如下所示:
(13)
(14)
从上式可以看出,TPR的值越大,表示识别准确度越高,分类识别的效果越好。同理,FPR的值越小,错误识别率就越低,分类识别的效果越好。数据库中joy、anger、sadness、pleasure四种情感样本各50个,基于以上提取的递归图特征参数,使用神经网络、K近邻、朴素贝叶斯、决策树这四种分类器均采用5倍交叉验证选择样本的训练集和测试集,计算每种分类器的TPR和FPR,如表1所示。
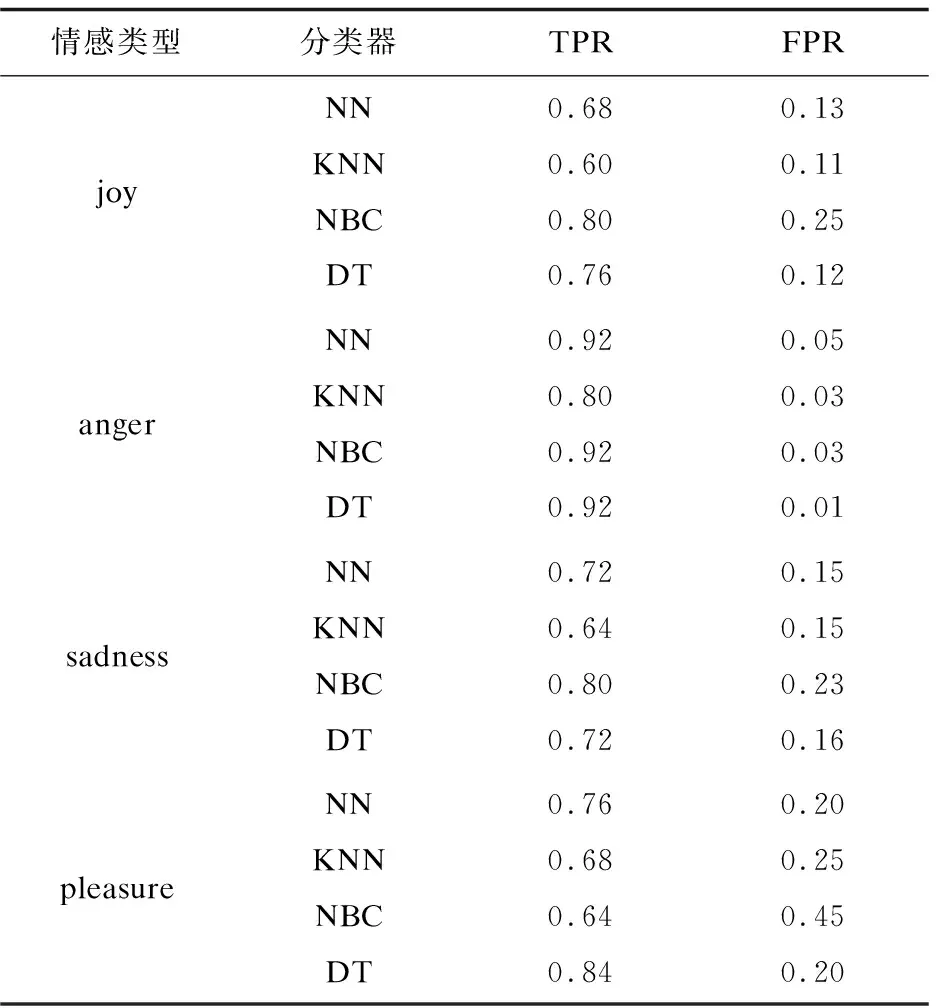
表1 基于递归图特征参数使用分类器计算的TPR和FPR
从表1可以看出,NBC对joy的识别性能最好,正确识别率为80%;在对anger情感进行识别的过程中,很明显KNN识别率较低,而其他分类器性能较好,识别率都为92%;在对sadness情感进行识别的过程中,NBC对sadness的识别性能最好,识别率为80%;在对pleasure情感进行识别的过程中,DT对pleasure的识别性能最好,识别率为84%。
另外,在常规统计特征中,同样使用神经网络、K最近邻、朴素贝叶斯、决策树这四种分类器均采用5倍交叉验证选择样本的训练集和测试集,计算每种分类器的TPR和FPR,如表2所示。
为了评估基于递归图特征与统计特征的情感识别性能,采用分类器识别结果的平均值作为识别性能的判断标准,则两类特征的识别对比如表3所示。
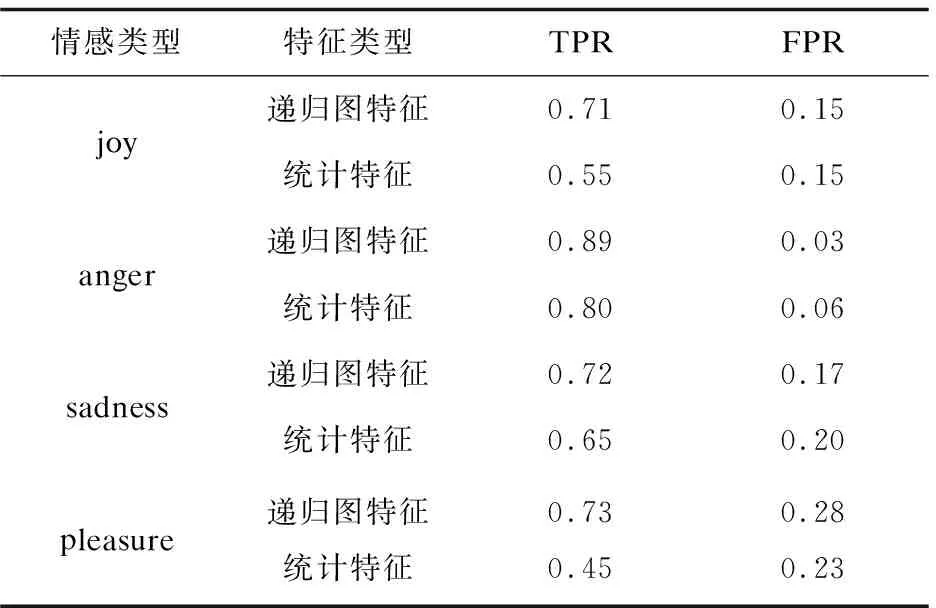
表3 递归图特征和统计特征情感识别性能对比
通过上面识别对比可以发现,基于递归图特征的情感分类识别率都要明显高于基于传统统计特征的情感识别率。而在错误识别率上,基于递归图特征的情感分类错误识别率基本上都小于统计特征的情感分类错误识别率。另外,对同样的样本,递归图特征只提取了10个特征,而传统的统计特征提取了21个特征。
综上所述,使用递归图特征进行情感识别的效果明显优于传统的基于统计特征的情感识别的效果,基于递归图特征的情感识别在提高识别结果精度上使用了更少的特征参数。
5 结束语
在物质生活比较发达的今天,人们更多地追求精神上的享受。基于生理信号的情感识别就是一个将科技直接转化为生产力和精神追求的重要技术。基于生理信号的情感识别以一种非侵入无损的方式反映人体的情感状态,这些情感状态的结果可以提供给人们有益的反馈和指导,使得人们的生活更加健康幸福。针对基于常规统计特征的方法在情感分类识别效果上不理想的问题,在研究人体生理信号的基础上,提出了基于递归图和递归定量分析相结合的方法,提取了生理信号递归图中的10组非线性特征。理论分析和实验结果表明,基于递归图特征的情感分类识别率都要明显高于基于传统统计特征的情感识别率。而在错误识别率上,基于递归图特征的情感分类错误识别率基本上都小于基于统计特征的情感分类错误识别率。充分说明了基于递归定量分析的生理信号情感识别的优越性。目前只是研究了递归图中的非线性特征,未来可以提取更多的非线性特征构建模型,从而进一步提高情感识别效果。

