基于Nelder-Mead算法的3D打印模型最优化放置
秦 爽,黄先锋,张 帆,陈 伟,向东清
(1.武汉大学 测绘遥感信息工程国家重点实验室,湖北 武汉 430079; 2.珠海赛纳打印科技股份有限公司,广东 珠海 519060)
0 引 言
3D打印是以三维模型文件为基础,运用可粘合和可固化的离散材料(粉末、液体、丝等)为打印介质,通过分层打印、逐层堆叠累积的方式来制造物体的技术[1]。3D打印能快速而准确地将任意复杂的模型数据制造出实物,同时也带来了如打印成本优化等新的研究问题[2]。一般用于3D打印的材料价格是远远高于传统制造方式的,因而节省打印耗材成为降低打印成本的重要方法之一[3]。针对这一问题,许多学者通过优化3D打印模型的内部结构来减少打印模型耗材。例如,Wang等提出了一种基于“蒙皮-刚架”(skin-frame)的轻质结构来减少打印耗材[4];Kindinger等提出基于泡沫、轻木等轻质结构来减少3D模型重量[5];Lu等利用蜂窝结构思想提出一种打印模型内部掏空优化算法[6];Chen利用蜂窝六边形的网孔结构来填充内部挖空[7]。
目前,3D打印软件在节材优化方面上仍十分有限,如果不能合理地设计出打印模型内部结构,在对物体的镂空厚度和密度这些参数进行设定时仍然需要根据用户的经验,不合理的设计会导致打印出的模型不能满足于实际生产应用,还浪费了昂贵的打印材料[8]。3D打印材料消耗除了模型耗材外,还包括打印支撑结构耗材。为了让打印材料在有悬空的地方沉积,通常需要在模型有悬空部位的下方添加支撑材料[9-11]。因此,文中是在不改变模型原有内部结构的前提下,通过对打印模型最优化放置的研究来减少打印支撑耗材。
此外,与传统的制造技术相比,3D打印技术已大大缩短了模型输出时间,但是打印一个物体仍需花费不少的时间[2,12-13]。在打印过程中,还需考虑打印时间问题,通过缩短3D打印时间从而实现对产品对象的快速打印[2,14-15]。
文中针对打印耗材和打印时间两个方面进行优化,利用打印模型的支撑结构耗材体积和打印时间这两个参数以及各自所占的权重系数构造出目标函数,采用经典的Nelder-Mead算法,在不改变模型内部结构的前提下,计算出打印模型的最优摆放角度,以实现对打印模型的最优化放置,达到降低成本的目的。
1 模型支撑耗材体积计算
如图1所示,支撑耗材体积(Vs)计算思路为,将模型的上顶面投影到打印平面的体积(Vp)减去模型实体体积(Vm),即Vs=Vp-Vm,因此,可拆分为模型顶面投影体积计算和模型实体体积计算两个部分。
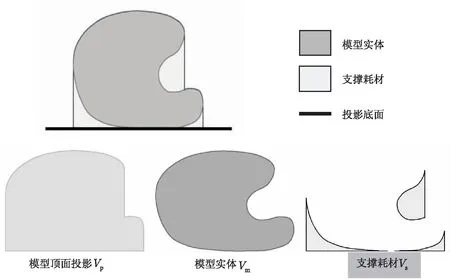
图1 模型耗材显示图
1.1 模型实体体积计算
文中分析的三维模型数据为三角网模型,由顶点和三角形构成,三角形的法向量满足右手准则,即所有三角形面片的法向一致,均指向体外。
设三维模型中的任意一个三角形顶点为A(x1,y1,z1),B(x2,y2,z2)和C(x3,y3,z3),如图2所示,以坐标原点O(0,0,0)为顶点,以ΔABC为底的三棱锥的体积为:
如果ΔABC为顺时针排序,根据右手准则,右手握拳方向为ΔABC的排序方向,大拇指指向为三角形法向的方向,那么原点O在ΔABC法向的正方向上,则VOABC为正数,反之VOABC为负数[10]。
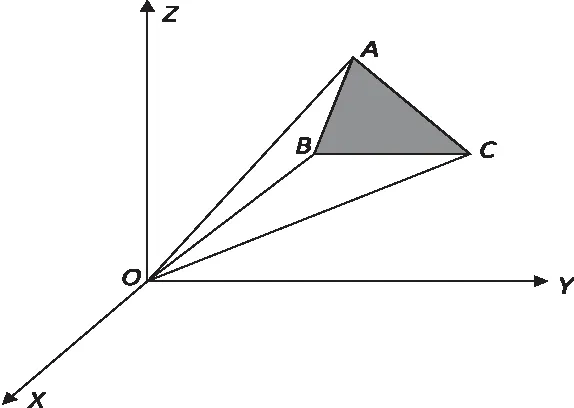
图2 模型体积计算
对任一给定三维模型数据,它的模型表面是由n个三角形面片组成,如果以坐标原点O为顶点,依次以这n个三角形为底可以构成n个三棱锥,那么该三维模型的体积计算公式为:
其中,Vi为第i个三角形与坐标原点构成的带符号的体积,其正负符号根据坐标原点O和该三角形法向量的正负方向确定。
1.2 模型顶面投影体积计算
体积计算需要逐个单元进行分析,三维显示引擎OpenGL提供了快速的几何模型投影计算能力。利用OpenGL的成像机理和深度缓存机制来计算打印物体在正射投影下的体积。
1.2.1 模型变换矩阵的计算
假设模型变换矩阵为Mv,模型绕X轴、Y轴和Z轴旋转的角度分别为DX、DY和DZ。为了使模型围绕自身坐标轴进行旋转,首先对模型进行平移变换,将模型移动到坐标原点,然后进行旋转变换,最后又利用平移变换将模型移动到模型的中心点。由于缩放矩阵会改变模型的大小,因此在计算过程中不考虑缩放矩阵的影响,具体步骤为:
(1)将旋转角度转换为弧度:
将模型移到坐标原点的平移矩阵为T1,遍历场景中模型所有的顶点坐标,得到在X轴、Y轴和Z轴方向上的最大值和最小值,假设分别为Maxx、Minx、Maxy、Miny、Maxz和Minz,并求出模型的中心点坐标(Xc,Yc,Zc)。满足以下关系式:
Xc=(Maxx+Minx)/2
Yc=(Maxy+Miny)/2
Zc=(Maxz+Minz)/2
(2)模型绕X轴、Y轴和Z轴的旋转矩阵分别为Rx、Ry和Rz:
(3)将模型移到物体的中心的平移矩阵为T2:
(4)模型变换矩阵Mv为:
Mv=T2×Rz×Ry×Rx×T1
通过模型变换矩阵和实物模型做相乘运算可以确定三维模型最终的大小、形状和位置,从而可以计算在当前旋转角度下的模型顶面投影体积。
1.2.2 模型顶面投影体积计算
根据计算出来的模型变换矩阵,可以得到模型在经过变换之后的坐标,从而可以计算出模型在X轴、Y轴和Z轴方向上的最大值和最小值,假设分别为Xmax、Xmin、Ymax、Ymin、Zmax和Zmin。
在OpenGL中提供了正射投影和透视投影这两种不同的投影类型。正射投影的投影线互相平行,投影的结果与原来的物体大小相等,符合文中的需求,因此将投影方式设置为正射投影。根据正射投影可以得到打印模型所有的顶面区域,读取系统计算的深度缓存信息得到视口范围内的深度值。
将每一个像素的深度值与初始深度值进行比较,依据深度缓存原理,如果该像素深度值小于初始深度值,则说明该像素点是物体所在的像素点。然后利用gluUnProject函数将所有物体所在的像素点实现屏幕坐标向世界坐标的转换,这样每一个物体所在的像素点都对应一个世界坐标。
通过相邻像素点的坐标值可以求出单个像素的边长,计算其面积S,将打印模型顶面区域所在的像素点的Z坐标值减去Zmin,累加值记为Zsum,则物体在Z轴正射投影下的体积Vp可表示为:
Vp=S×Zsum
2 模型打印时间计算
文中提出了一种打印时间的计算方法。假设打印模型所需的时间为ht,模型的总层数为R,每一层的厚度为dmm,每层打印所花的时间为h,存在这样的关系:
ht=R×h
R=(Zmax-Zmin)/d
设每一层的切片长(设定为沿X轴方向)为Lmm,宽(设定为沿Y轴方向)为Wmm,根据1.2.1节有:
L=Xmax-Xmin
W=Ymax-Ymin
喷头长度为kmm,打印字车在X轴的运行速度为Vxm/s,打印字车在Y轴运行速度为Vym/s,打印机头走过同一个图像区域的次数为m,打印字车从打印结束点回到打印起始点所用耗时为S(S一般为常量),则完成每层打印所需的步径数E(向上取整)为:
E=W/(k/m)+3
每层打印耗时为:
可以看出上式中的L、W和R三个变量与模型的摆放有关。
3 基于Nelder-Mead的最优函数求解
通过计算物体在任意放置角度下的打印支撑耗材体积fv和打印时间ht,构造一个目标函数F,F=a×fv+b×ht,其中a和b为各自的权重系数,fv和ht的大小与模型的摆放有关,利用单纯形算法求出F的最小值,得到模型绕X轴、Y轴和Z轴旋转的最优放置角度。
3.1 Nelder-Mead算法
Nelder-Mead算法是一种求解多维函数极值的算法,由于该算法运用了单纯形的概念,因此又称单纯形算法。一个n维单纯形是指包含n+1个节点的凸多面体,例如,一维单纯形是直线上的线段,二维单纯形是平面中的三角形,三维单纯形是三维空间中的四面体。
3.2 算法思路和流程
文中研究的是3D打印模型的最优化放置功能,最终需要解算出待打印绕X轴、Y轴和Z轴所旋转的最佳角度,构造的目标函数有3个角度变量,为三维单纯形,在变换过程中只改变顶点的位置和尺寸,几何形状和维度保持不变,始终保持一个4个点的点集,即为三维空间中的四面体。
具体的算法如下:
输入:模型绕X轴、Y轴和Z轴旋转的角度DX、DY和DZ以及打印支撑耗材体积和打印时间所占目标函数的权重系数a和b
输出:在该权重系数下使得目标函数值最小的DX、DY和DZ
Step1:在进行每次迭代之前,分别计算4个点对应的函数值,并对各自的函数值进行排序,使其满足:
f(x1)≤f(x2)≤f(x3)
Step2:找出目标函数最大值fh,次大值fs以及最小值fl,各自对应的点分别为xh、xs和xl,其中h=4,s=3,l=1。
Step3:计算重心点c,c为包含最好的3个点的多面体的中心,即除点xh外其他点的平均值:
Step4:对单纯形进行变换操作,通过使用反射、扩张或收缩产生的新的点来尝试替代最差的点xh,直到满足收敛条件,得到新的单纯形,从而得到最好的点。
图3为具体的计算过程。
4 实验结果
利用VS2013开发工具和OpenGL函数库,通过VC++实现了所提出的优化算法,其中用户界面基于Qt进行开发。实验中每层切片的厚度d为0.028 mm,喷头长度k为54 mm,采用4pass打印,即m为4,打印字车在X轴的运行速度Vx为0.6,Vy为0.1,s为1.5 s。图4(a)为模型在初始状态下的放置图,在权重系数框中输入0到1之间的实数,构造出关于打印模型支撑结构耗材体积和打印时间的带有权重的目标函数。图4(b)为打印时间权重为0、耗材权重为1得到的打印支撑耗材最优放置图;图4(c)为打印时间权重为1、耗材权重为0得到的打印时间最优的放置图。
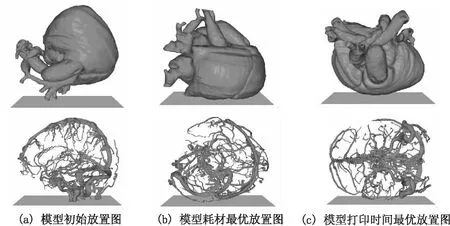
图4 各种状态下的模型放置图
如表1和表2所示,在不改变模型内部结构的前提下,使用文中算法可以明显减少打印支撑耗材体积,提高打印速度,从而达到降低成本的目的。
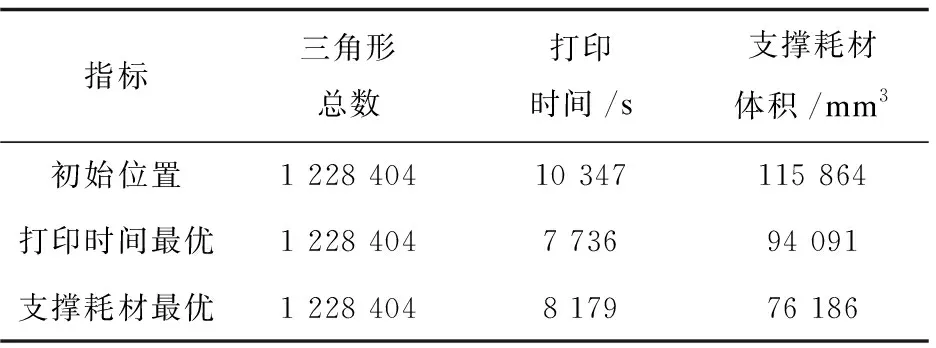
表1 心脏在各种摆放状态下的打印成本
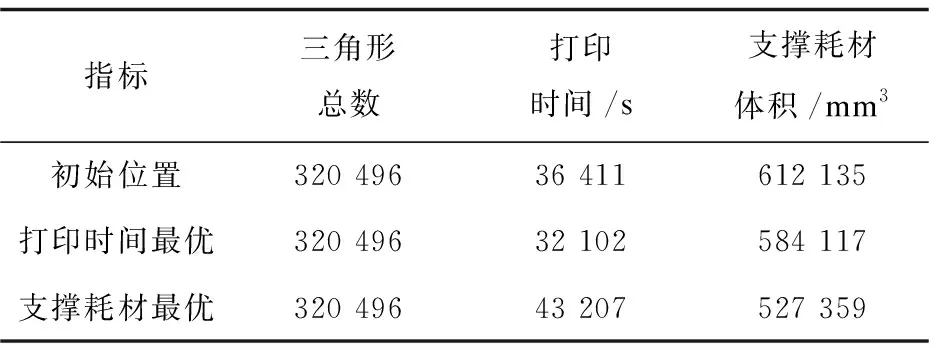
表2 血管在各种摆放状态下的打印成本
5 结束语
针对目前3D打印材料费用昂贵、打印成本高的问题,提出了一种基于Nelder-Mead的优化算法。该算法计算出了模型在任意摆放角度下的支撑结构耗材体积和打印时间,通过不断地迭代实现了对模型的最优放置,从而减少了打印支撑结构耗材、缩短了打印时间,达到了降低3D打印成本的目的。
该优化算法主要应用于软材质实心打印材料,用于医学手术模拟训练和手动切割,因此,没有考虑模型的内部结构优化。未来需要考虑内部支撑结构的优化,从而适应更多的打印需求。

