基于参数融合的Q学习交通信号控制方法

刘成健，罗 杰

(南京邮电大学 自动化学院，江苏 南京 210000)

0 引 言

目前，随着人口增长及科学技术的高速发展，城市交通流也在日益增大。在这种大环境下，需要一种行之有效的方法对交通流进行管理[1]。传统的控制方法对于日常的交通流无法做到很好的适应,于是人们开始尝试使用许多先进的控制理论和方法[2-3]。机器学习作为当下流行的科学技术，不断被研究者们引入交通控制领域[4-5]。其中，强化学习中的Q学习更是在此领域有着优异的表现，并成为一个研究热点[6-7]。

文中在Q学习算法中引入基于经验的状态划分对状态空间进行改进；并通过建立交通状态参数融合函数对复杂的交通参数进行优化；采用模糊技术实现Q学习算法中的奖惩机制。相对于固定周期的智能配时策略，文中通过获取当前绿灯相位以及红灯相位的交通流状态，实时为各相位提供合适的绿灯配时方案，以达到自适应控制的目的。

1 基于Q学习的改进控制方法

1.1 路口控制系统的组成

如图1所示，文中构建了一种基于Q学习的改进路口交通信号控制系统。该系统包括交通状态感应模块、参数融及划分模块、Q学习模块、控制决策模块、Q表、模糊评价器。

图1 控制系统模型

其中，各模块的功能如下所述：

交通状态感应模块：通过传感或图像处理技术采集各路口各车道上的车流量信息、上个周期车辆排队长度、路口各相位车辆延迟时间。

参数融及划分模块：配置在路口的控制节点中，针对感应模块采集到的交通参数通过式2进行融合，生成基于上述参数的交通参数s，并通过状态划分将其划分到对应的状态段S，用于在Q表中查询控制表得到配时方案以及用于Q学习模块对控制表的更新。

模糊评价器：根据感应模块采集到的参数，查询奖惩值反馈表，将查询到的奖惩值反馈给Q学习模块。

Q学习模块：配置在路口的控制节点中，接收参数融及划分模块传递过来的状态段集合S，将其和奖惩值r共同作为Q学习模块更新Q表的必要依据，通过式1对上一个状态的选择依据进行更新，并将S传递给Q表用于配时方案的查询。

控制决策模块：配置在路口的控制节点中，根据选择策略从Q表所传递的结果中选择合适的配时方案。

Q表：配置在路口的控制节点中，以表格的形式存储不同交通状态下的配时策略Q(S，a)，其中首列存储的是交通状态的状态段集合，首行存储的是不同的相位绿灯配时方案，Q表将根据经验预先初始化每个Q(S，a)，在随后的迭代过程中，Q学习模块不断地对Q(S，a)进行更新，直到获得不同交通状态下的最优配时策略。

该路口控制系统是一个闭环负反馈系统，根据经验初始化控制表之后，在学习未完成之前，系统将通过不断迭代对Q表进行更新，最终获得不同交通状态下的最佳配时方案。

1.2 路口交通信号控制Q学习

Q学习是由Watkins在1989年提出的算法，是一种无模型的在线强化学习算法[8-9]。Q学习中每个(状态，动作)对对应一个相应的Q值,在学习过程中根据Q值选择动作。Q值的定义是如果执行当前相关的动作并且按照某一策略执行下去,将得到回报的总和。在Q学习中，Q函数通过执行该动作后的回报以及遇到的下一个状态的预测值进行更新[10-11]。文中将其应用于交通控制领域，Q函数更新所用的公式为[12-13]：

Q(S,a)←Q(S,a)+α[r+γMaxa'Q(S',a')]

(1)

其中，S为交通状态s的状态段集合，a为交通配时方案，Q(S,a)表示当前状态集S下的选择依据；α为学习效率，α越高则表示Q(S,a)受下一个状态影响越大；r为执行配时方案a之后的反馈，即奖惩值；S'表示下一个状态集，Q(S',a')表示下一个状态集下的选择策略，Maxa'Q(S',a')则表示下一个状态集所估计的最佳选择策略；γ表示衰减度，γ越低，则系统学习效率受奖惩值r的影响越大。

1.3 交通状态描述

文中将w=(F,Lg,Lr)定义为绿灯相位通行繁忙度、绿灯相位车辆排队长度、红灯相位车辆排队长度三个维度的状态向量集。为提高Q学习对于道路状态变化学习效率与控制效果，根据参数融合思想，通过式2将描述当前交通状态的向量集w转化交通参数s。

(2)

其中，Tmin和Tmax是绿灯相位最短和最长有效时间；Fg为在绿灯相位车辆入口处设置的车辆繁忙度(Fg越高表示绿灯相位道路车辆越繁忙,反之表示道路车辆通行状况越好)；Lmax为道路所能接受的车辆排队长度极限；Lg为绿灯相位的车辆排队长度；Lr为红灯相位车辆排队长度。

当s越大，表示当前相位的交通状况越良好；当s趋向于0时，表示交通状况越差。式2的物理意义为：当红灯相位车辆排队长度越长而绿灯相位车辆排队长度越短且绿灯相位交通繁忙度较低时，系统倾向于给当前相位一个较短的绿灯时间。当红灯相位车辆排队长度越短，绿灯相位车辆排队长度越长且绿灯相位交通繁忙度较高时，系统则更倾向于为当前相位选择更长的绿灯配时。

交通配时采用有序相位循环配时方案，出于对实际情况的考虑，所有相位都会设置一个最小的绿灯时间[14]。

1.4 改进的Q表

根据路口的配时经验可知，如果当前相位路口的交通繁忙度较低，那么应该给此相位分配一个相对较短的绿灯时长；当繁忙度上升时，则给此相位分配的绿灯时长应该相应增多。而当处于某一交通状态时，为其配置过高或者过低的相位绿灯时间是非常不合理的。故而文中根据经验为当前相位每个交通状态配置一定数量的配时方案。这样，在Q表进行更新时，可以直接忽略掉那些劣质的选项。专注于对该交通状态下较好的几种配时方案进行学习更新，从而获得最佳的相位绿灯配时方案。根据上述规则，初始Q表设计成如表1所示的形式。

表1 Q表基本结构

其中，Si为存储在Q表中的状态段集合；a表示不同的相位配时方案；Q(S,a)表示在状态S下对于配时方案a的选择依据。

1.5 改进的Q学习奖惩机制

文中考虑了多影响因素评价所选择策略的控制效果，设计了基于模糊逻辑[15-16]的模糊评价器实现Q学习的奖惩机制。选取两个参数，作为基于模糊逻辑的模糊评价器输入，分别为：

(1)绿灯相位的通行繁忙度变化率F'(繁忙度F由式3定义)；

(2)红灯相位的车辆排队长度变化率Lr。

(3)

其中，q为绿灯相位在决策持续时间中的交通通过量；st为绿灯相位在决策持续时间中的饱和流量。

输入变量均采用五级模糊划分方式，即{“负大”，“负小”，“中”，“正小”，“正大”}，表示五种不同的排队长度以及交通繁忙度变化程度，均记为{NB,NS,ZO,PS,PB},使用三角隶属度函数表示。模糊评价器仅有一个输出，为奖惩信号值r，采用重心法对模糊输出进行解模糊，输出的奖惩信号值范围是(-1，1)。

1.6 改进方法的控制流程

结合上文所述，基于Q学习的交通控制方法实现步骤如下：

Step1:获取当前路口的交通状态，获取相应的交通状态参数，通过式2计算对应的交通参数s，通过状态划分确定s所在的交通状态段S；

Step2:Q表根据参数S给出合适的配时方案，经过决策过后执行；

Step3:交通流状态改变后，继续采集当前状态下的交通参数；

Step4:在绿灯有效时间内，将获取的交通状态参数与上一时刻的交通状态参数进行比较，将差值传入模糊评价器中进行查询，得到奖惩值r；

Step5:在下个相位开始前(设置绿灯间隔为2 s)，根据式1更新控制表对应的Q(S,a)；

Step6:当前绿灯相位配时方案结束后，切换至下一个相位；

Step7:重复Step2～Step6。

2 仿真实验

微观交通仿真是评价信号控制策略的有效方法[17]。文中利用VISSIM搭建用于仿真实验的路口模型，结合Matlab加载不同的交通信号控制算法，以此为平台验证算法的有效性。所采用的路口模型仿真模型如图2所示。

图2 四相位路口模型

其中，每条路段包括四个车道，一条为左转弯车道，两条直行车道，一条右转弯车道。车辆在交叉口处的转弯概率分别为左转弯30%、直行40%、右转弯30%。内部路段长度均为200 m。车辆平均行驶速度为40 km/h。路口车道的交通流量设置如表2所示。

表2 路口交通流量

在仿真过程中，设定车辆排队最大长度200 m，车辆通行繁忙度F的范围为0～1。设定绿灯的最低有效时长为25 s，最高75 s。通过式2乘以影响因子计算后得到的交通参数s范围为0～15，其中s越大，表示道路交通状况越好。初始Q表中每一个交通状态集S下根据经验选择4种不同的配时方案进行交通控制。

作为比较，另采用了传统强化学习对交通流进行控制，利用VISSIM对控制效果进行采集，结果如表3、表4所示。

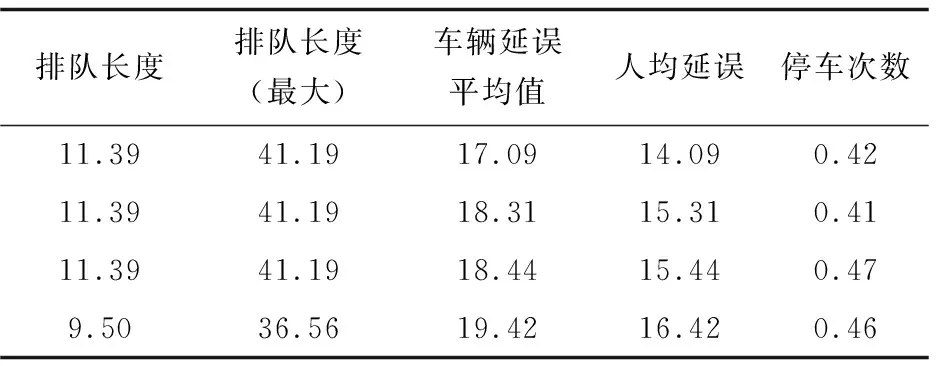
表4 基于Q学习改进方法控制结果反馈

分析表格可以看出，使用基于Q学习的改进交通控制方法后，车辆总体延迟上比传统强化学习控制缩短了约16%；另外在排队长度及总体停车次数等指标上均优于传统强化学习控制。

3 结束语

文中将模糊技术与Q学习相结合，利用参数融合及状态划分的思想对Q表进行改进，同时通过给出基于相位的绿灯配时方案，实现了路口交通的自适应控制。提高了控制系统针对多样化交通流状况响应的实时性，并通过仿真做出针对改进的有效性验证。另外每个路口控制系统通过接收相邻路口的交通流信息，多个路口组合之后，有希望应用于城市区域道路交通控制，形成基于多智能体的交通控制网络。