基于dSPACE的汽车自动变速器换挡规律优化硬件在回路仿真

卢晓晖, 张智超, 李 哲

(1.长春工业大学 汽车工程研究院， 吉林 长春 130012;2.长春工业大学 机电工程学院, 吉林 长春 130012)

0 引 言

传统自动控制系统开发过程中，需要不断反复测试和修改软件代码，往往系统硬件完成后才暴露出问题，硬件架构要有所优化调整，随之依托于硬件的软件编码也要改善。在控制系统越来越复杂化的今天，这样使得研发周期无限期延长、研发费超支，控制系统的鲁棒性得不到保障，甚至具有良好潜在价值的优秀项目都有可能付之东流。为了避免这样的损失发生，融入新型“V”开发模式的快速控制原型技术(Rapid Control Prototype, RCP)和硬件在回路仿真(Hardware in Loop, HIL),主要是通过在虚拟环境中对产品进行设计，以此达到降低产品的设计周期以及所花费的成本[1-3]。

dSPACE实时仿真系统是一个基于半实物仿真及MATLAB/Simulink控制系统的软硬件工作平台，dSPACE系统具有实时性强、可靠性强、扩充性好等优点，而且系统中的处理器具有很强的计算性能，可以根据自己的需要进行组合[4-6]，很好地实现代码的自动生成、下载、调试等功能。dSPACE系统具有高度的模块性和集成性，允许用户无论是在软件还是硬件可以根据需要来创建自己的系统，对被控制的对象进行研究，验证所建方案的正确性，提高了开发的效率。

文中基于dSPACE软硬件搭建了汽车自动变速器换挡规律优化方案的硬件在回路仿真平台，并针对运行用动态规划理论制定出的换挡规律进行了快速控制原型仿真实验。

1 离线仿真模型的搭建

整车仿真模型作为换挡决策优化设计过程中的重要部分，其精度的优劣决定了仿真实验结果的准确性与合理性[7]。为了高精度描述整车系统，文中采用商业仿真软件AMESim和Matlab/Simulink作为平台搭建了五挡AMT乘用车仿真模型。

在AMEsim软件中搭建整车模型，包括驾驶员、发动机、整车、变速器、行驶工况模块五大模块。在Simulink中运用stateflow搭建了换挡逻辑控制模块。两者共同组成离线联合仿真实验平台。

汽车整车模型如图1所示。

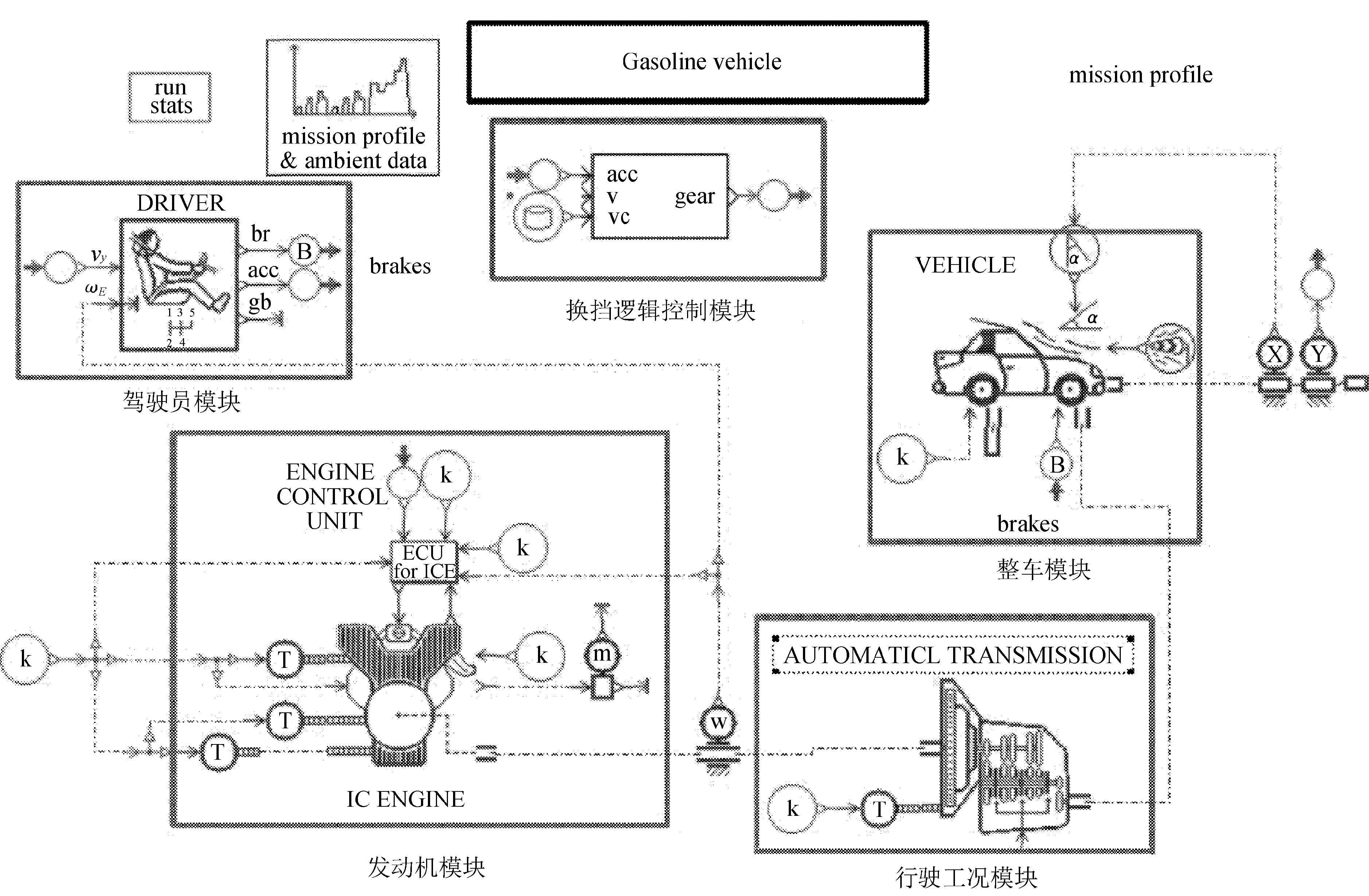
图1 汽车整车模型

1.1 驾驶循环工况模块

选取三个循环工况对汽车的行驶状况进行模拟，分别是时间为1 180 s的NEDC、1 370 s的UDDS和660 s的1015工况。NEDC、UDDS和1015循环工况下车速与时间的关系如图2所示。

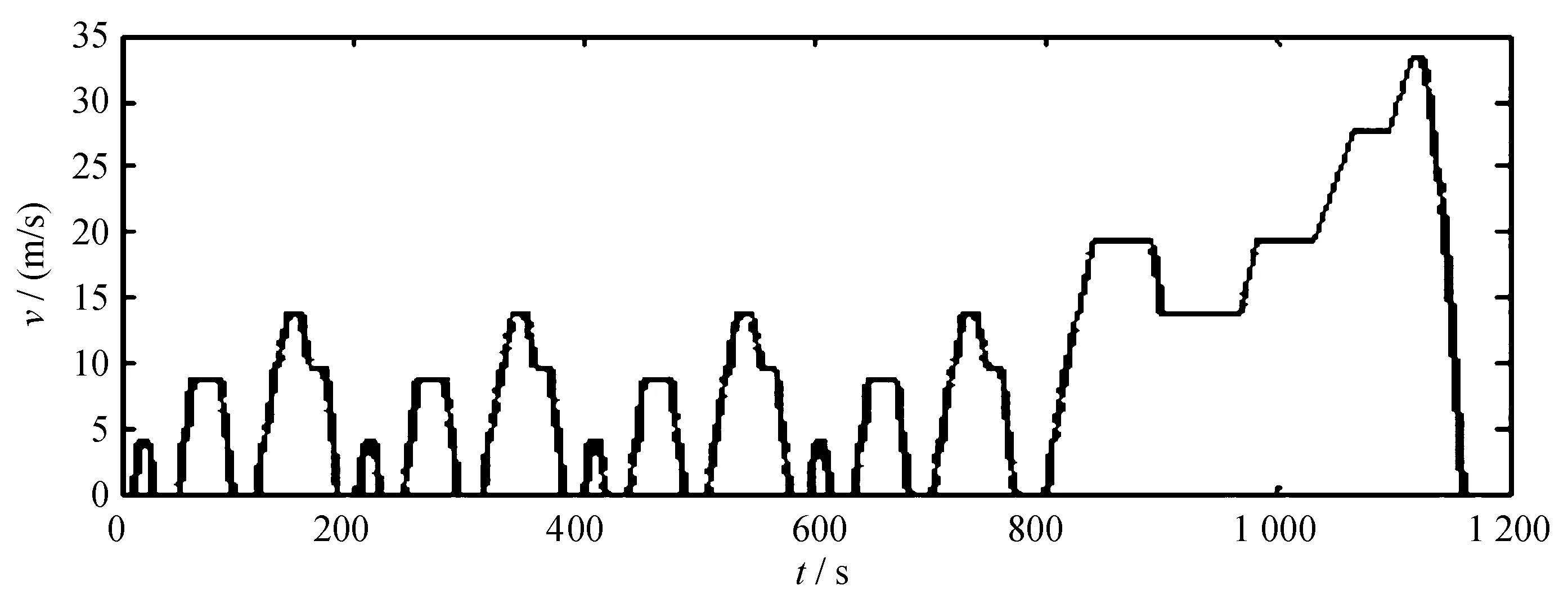
(a) NEDC工况

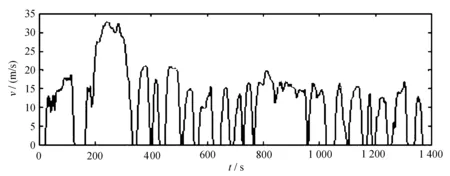
(b) UDDS工况

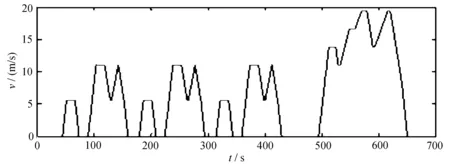
(c) 1015工况

1.2 Simulink控制策略

在MATLAB/Simulink中进行换挡逻辑控制模块的搭建，分别在AMESim和Simulink中添加interface接口和s-function函数进行信息的交互传递，利用Stateflow建立了换挡逻辑控制器，实现各挡位之间的相互转换,Stateflow换挡原理部分如图3所示。

图3中，共有6个挡位状态，其中gear_e=0表示为空挡。每两个相邻的挡位之间分别通过“up”和“down”这两个状态迁移事件来实现挡位之间的迁移。行驶过程中，挡位的变换过程见图3下框，实时车速v与换挡规律中的升挡点的值Vup满足表达式「v>up_th1」，则up事件被激活，进行升挡操作，即挡位从初始稳定状态“steady-state”迁移至升挡状态“upshifting”，同时挡位状态gear也被更新并记忆保存。挡位就沿着升挡事件up的箭头升向高一级的挡位。同理，当车速v与降挡点值Vdown满足表达式「v>down_th1」，则down事件被激活，进行降挡操作，即挡位从初始稳定状态“steady-state”迁移至降挡状态“downshifting”，同时挡位状态gear也被更新并记忆保存。挡位就沿着降挡事件down的箭头降到低一级的挡位，完成降挡过程。

AMESim模块：此模块负责与整车模型实现实时通讯，将得到的实时仿真数据反馈到Simulink工具箱中搭建的换挡逻辑控制器模块中进行运算，并且能在各模块中提取相应仿真工况下数据参数，供分析使用，如发动机转速、转矩、油门开度等。

Simulink中的换挡逻辑控制模块：汽车实时状态与已经储存制定好的换挡规律不停地进行比较，当车辆的状态数据满足换挡规律中的换挡要求时，车辆的换挡规律控制器就被激活，根据换挡规律做出升挡或者降挡的决策。若未达到换挡规律的换挡条件，则维持当前挡位。

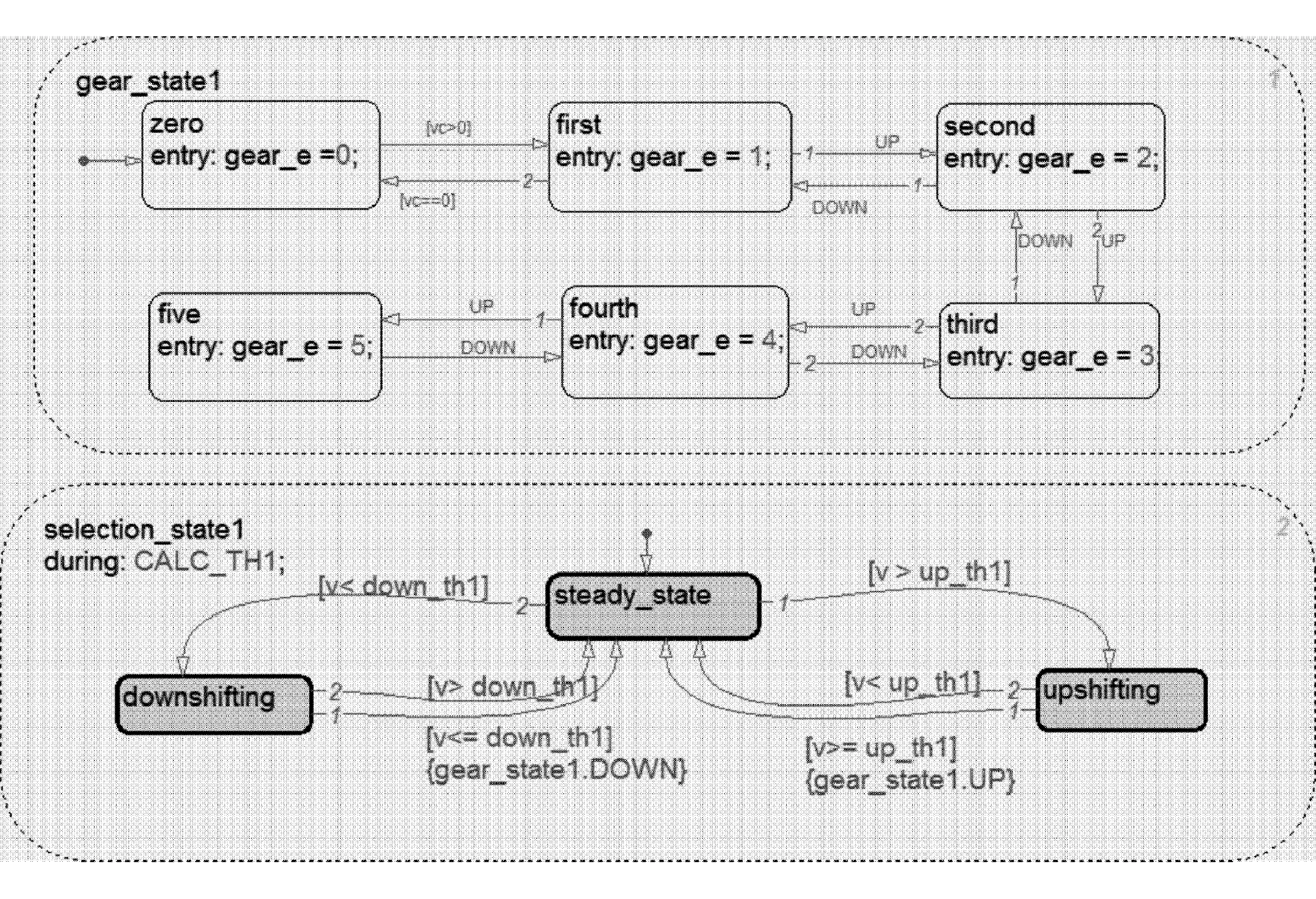
图3 控制逻辑Stateflow

汽车实际状态的参数与制定好的换挡规律参数进行不断的对比，如果车辆的实际状态达到换挡要求，则汽车执行换挡，如果实际数据没有达到换挡要求条件，则汽车保持当前挡位不变。

2 基于动态规划理论的换挡规律制定

2.1 动态规划算法

动态规划既是一种数学优化方法，也是一种计算机编程方法。在这两种情况下，是以递归的方式将复杂的问题分解成更简单的子问题来简化。虽然某些决策问题不能以这种方式分解，但跨越几个时间点的决策往往会递归地分解，贝尔曼将此称为最优性原则[8-9]。同样，在计算机科学中，通过将问题分解成子问题，然后递归地找到子问题的最优解，就可以得到最优的子结构。如果子问题可以递归地嵌套在整体的大问题中，从而使动态规划方法适用，那么大问题的解与子问题的解之间就有关系了。在相关优化算法文献中，这种关系被描绘为贝尔曼方程。

动态规划有如下特点[10]：

1)从终点开始整体决策最优路线，先通过递推法比较各段性能指标，然后正向计算完成整体决策，将一个多阶段决策问题转化为多个单段决策问题来处理。

2)动态规划的理论基础是最优性原理，而最优性原理能将一个N段最优决策问题转化为N个一段最优决策问题，与穷举法相比，可大大减小计算量。

2.2 状态变量和控制变量的确定

在对AMT汽车传动系工作过程进行分析之后，确定将挡位ng(k)作为状态变量，换挡命令ug(k)作为控制变量。

状态变量转移方程为：

ng(k+1)=f(ng(k)+ug(k))

(1)

其中，f为动力学系统函数，对离散的换挡指令ug(k)施加一个约束会影响到换挡的动力性，并且也会影响到优化后的结果。对于5速AMT，ug(k)本应属于集合{-5,…,-1,0,1…,5}。但考虑到汽车驾驶性能的问题，选择ug(k)={-1,0,1}作为换挡指令，以避免在某一时刻的换挡过程中发动机转速发生巨大变化。鉴于AMT的平均换挡时间少于1 s，在1 s的时间步长内只降或者升一个挡位是合理的。其中，“-1”代表降一个挡位；“0”代表维持当前挡位；“1”代表升一个挡位。

由于实验对象为5挡AMT，齿轮的速比是离散间断的，无法对速比进行关于时间的求导运算。因此，需要对AMT汽车传动系模型进行离散化处理，离散后结果如下：

(2)

2.3 目标函数的建立

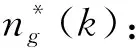
(3)

优化目标函数：

(4)

式中:Q----燃油消耗量，g；

b(k)----燃油消耗率，g/(kW·h)；

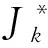
2.4 约束条件和惩罚函数

动态规划理论是解决多阶段决策优化问题的最佳方法。动态规划多阶段决策过程如图4所示。

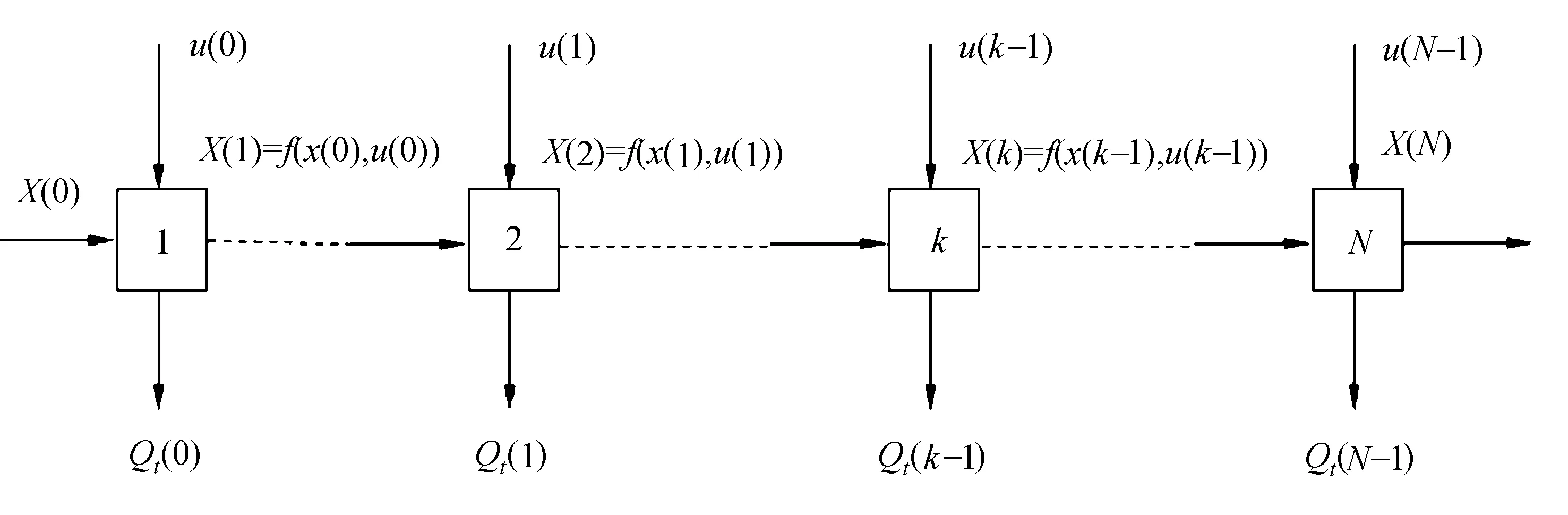
图4 动态规划多阶段决策过程

图4为一个多阶段决策过程，在循环工况k时刻，状态变量为挡位ng(k)，控制变量为换挡指令ug(k)，优化目标为燃油消耗量Q(k)。

在优化过程中，有必要考虑由物理限制引起的约束，以确保发动机的安全和平稳运行。一般来说，这些约束可用数学形式表达：

ωmin≤ω(k)≤ωmax

0≤Te(k)≤Te,max

(5)

式中:ωmin----发动机最小转速;

ωmax----发动机最大转速;

ω(k)----k时刻发动机转速；

Te,max----发动机最大转矩;

Te(k)----k时刻发动机扭矩。

变速器中的约束变量为：

(6)

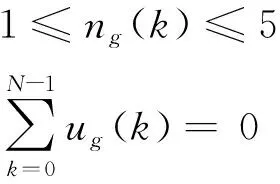
(7)

在紧急加速和制动的工况下，由于相对于油门和制动突然变化，车速的变化会滞后一些。这样很容易会使AMT汽车产生循环换挡现象。而这些循环换挡是没有必要的，不仅加快了变速器和离合器部件的摩擦损耗，还会减少变速器体内啮合齿轮的使用寿命，降低乘车舒适性，增加油耗[11]。因此，需要设置换挡频繁惩罚函数来抑制循环换挡现象的发生，其函数为：

nk=λ|ng(k+1)-ng(k)|

(8)

式中:λ----限制换挡次数的权重因子。

因此，目标函数的最终表达式为：

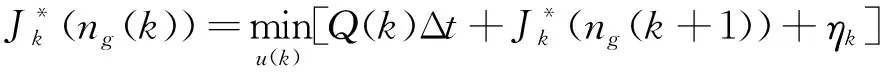
(9)

2.5 动态规划最优解

动态规划是解决非线性、非凸优化问题强有力的方法。在混合多种约束的情况下，能获得一个具有全局优化性、时变和状态反馈的解决方案。通过上述对动态规划过程的分析，其递归方程如下：

第N步：

(10)

第k步，k∈[0,1,…,N-1]：

(11)

从循环工况第N阶段开始至第1阶段结束，递推计算根据状态转移方程得到各时刻所有状态变量ng(k)值上的最优控制解。递推计算完成后进行递归计算，获得各时刻相应状态取值点的最优控制解，递归计算完成后，全部动态规划计算过程结束，便得出整体循环工况下全局最优控制解。

五挡AMT汽车分别在这三个循环工况下的优化计算结果如图5所示。

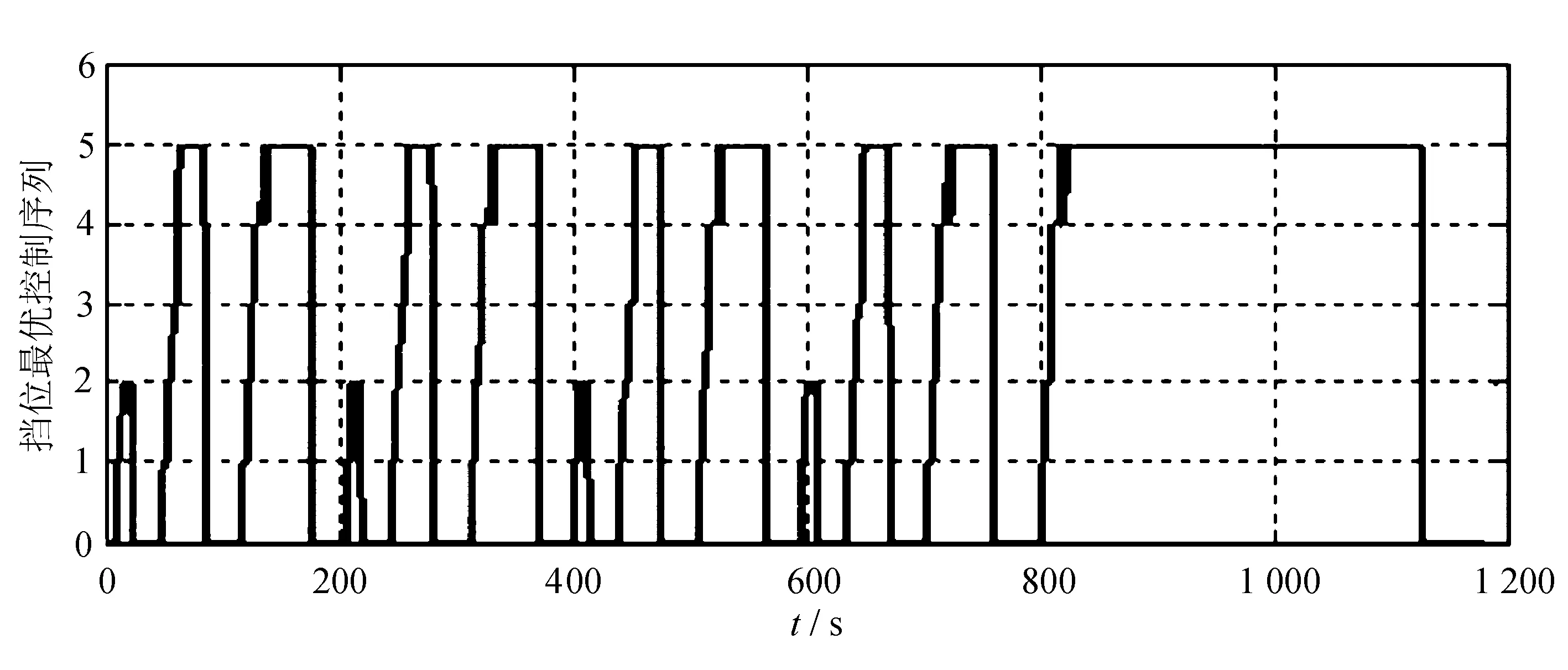
(a) NEDC工况

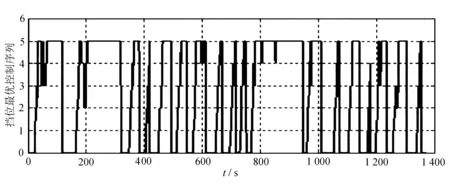
(b) UDDS工况

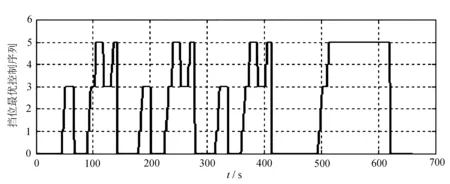
(c) 1015工况

这三张图分别是运用动态规划算法计算出在NEDC、UDDS和1015工况下，燃油消耗最小的挡位序列最优解。也就是说，按照图中换挡时刻和挡位在对应工况下进行换挡操作，整个工况下来，油耗量是最少的。

2.6 换挡规律制定

以NEDC工况为例，把仿真模型行驶工况设为NEDC，将运用动态规划算法在NEDC循环工况下得出的挡位最优控制序列解制成表格，作为整车仿真模型中变速器模块端口1的输入。

将仿真时间设置为1 180 s，运行整车模型。在仿真结束之后，分别提取发动机模块中的油门开度、驾驶员模块中的车速和变速器模块中的挡位数据。然后，分别对1015和UDDS设置660 s和1 370 s的仿真时间，提出对应的油门开度、车速以及挡位数据。

分别将这三个工况下所提取的信号数据共同画到一张图上，如图6所示。

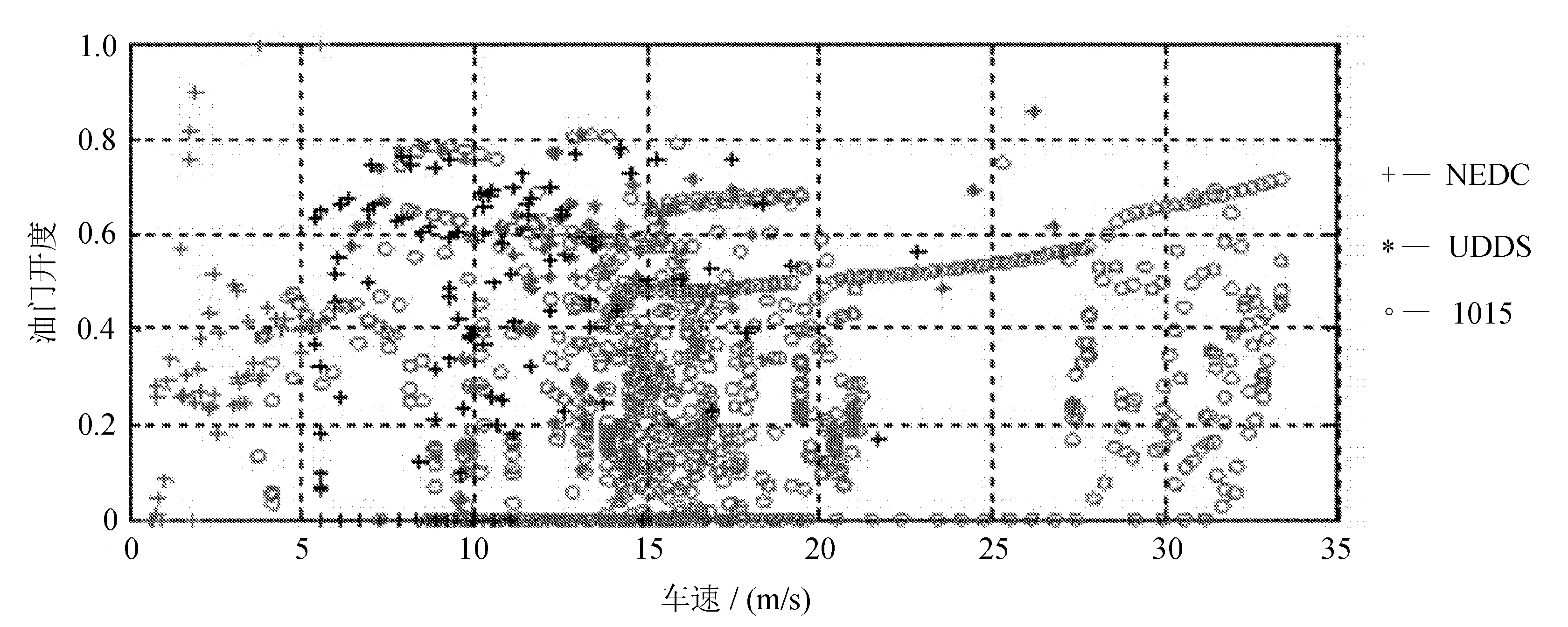
图6 NEDC、UDDS和1015三种循环工况下变速器挡位工作点分布

不同颜色和形状的点代表五个挡位的工作点部分情况。由图中可以看出，变速器1挡工作点主要分布在0～5 m/s的车速范围内；变速器2挡工作点主要分布在4～10 m/s的车速范围内；变速器3挡工作点主要分布在8～15 m/s的车速范围内；变速器4挡工作点主要分布在10～15 m/s车速范围内；变速器5挡工作点主要分布在13 m/s以上的车速范围内。其中，1挡和2挡的工作点重合区域大致在2～6 m/s的车速之间；2挡和3挡的工作点重合区域大致在4～14 m/s的车速之间；3挡和4挡的工作点重合区域大致在6～18 m/s的车速之间；4挡和5挡的工作点重合区域大致在9～28 m/s的车速之间。

在相邻挡位重合区域部分作出的换挡曲线就是同时满足多个循环工况经济性要求的基于动态规划的换挡规律map。在相邻挡位工作点重合区域部分初步制定出换挡规律的升挡线。文中采用以车速v和油门开度d作为换挡控制参数，为了避免换挡循环和频繁换挡现象的发生，用等延迟法制定出与换挡规律升挡线相应的降挡线[12]。制定出的基于动态规划理论的换挡规律map图如图7所示。

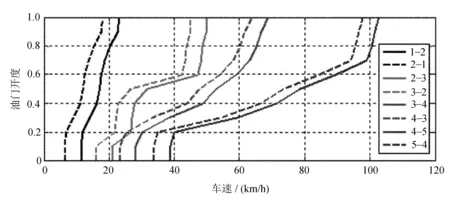
图7 基于动态规划理论制定的换挡规律map图

3 快速控制原型仿真实验

为验证换挡逻辑控制器的实时性能及基于动态规划的换挡规律有效性，制定实时实验方案，如图8所示。

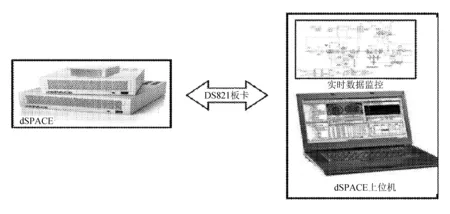
图8 实时实验设计方案

在AMEsim中搭建的整车模型通过s-function与Matlab/Simulink搭建的换挡控制器联合，利用MATLB的RTW模块生成实时代码。然后，通过dSPACE上位机专用通信板卡下载至dSPACE主机中，这样可以很好地模拟虚拟仿真控制对象。

实验时，首先要把在电脑机上完成的整车搭建模型和控制器转换为可执行的程序代码写入到dSPACE主机中，然后通过主机对可识别代码的运行来实现对控制有效性的验证工作。在此过程中，如何将控制方案用代码的方式得以实现是一个重要的环节。在模型搭建方面，文中用到了AMEsim和Matlab/Simulink两个软件，所以在实验前要在这两个软件中进行环境设置工作。

实时实验实物图如图9所示。

图9 实时实验实物图

实验设备dSPACE应用A/D，D/A模块接口，并配备了DS1006处理器以及DS2211 I/O 板卡，运行仿真步长设为1 ms，仿真时间为1 180 s。分别提取了NEDC工况下的发动机转速、转矩挡位、油门开度和油耗情况，如图10所示。

从图10可以看出，发动机转速大致分布在1 000～3 500 r/min之间，最高转速为3 483 r/min，多为发动机高效区工作；发动机扭矩输出正常，最大扭矩为134 N·m；换挡过程中没有循环换挡和频繁换挡的现象发生；油门开度均在0.8以下，没有急加速情况，都在合理范围内。这说明实时实验过程中车速跟随性较好，动力性良好。最终油耗为634.8 g，相比基于动力性换挡规律的油耗减少了5%。综合以上结果，实时实验表明了这个控制方案具有很好的实时效果。基于dSPAEC系统的实时仿真实验结果与AMEsim和MATLAB/Simulink联合离线仿真实验结果基本一致。这验证了换挡规律控制方案的有效性，为以后的控制器硬件实现和实车实验验证打下了良好的基础。

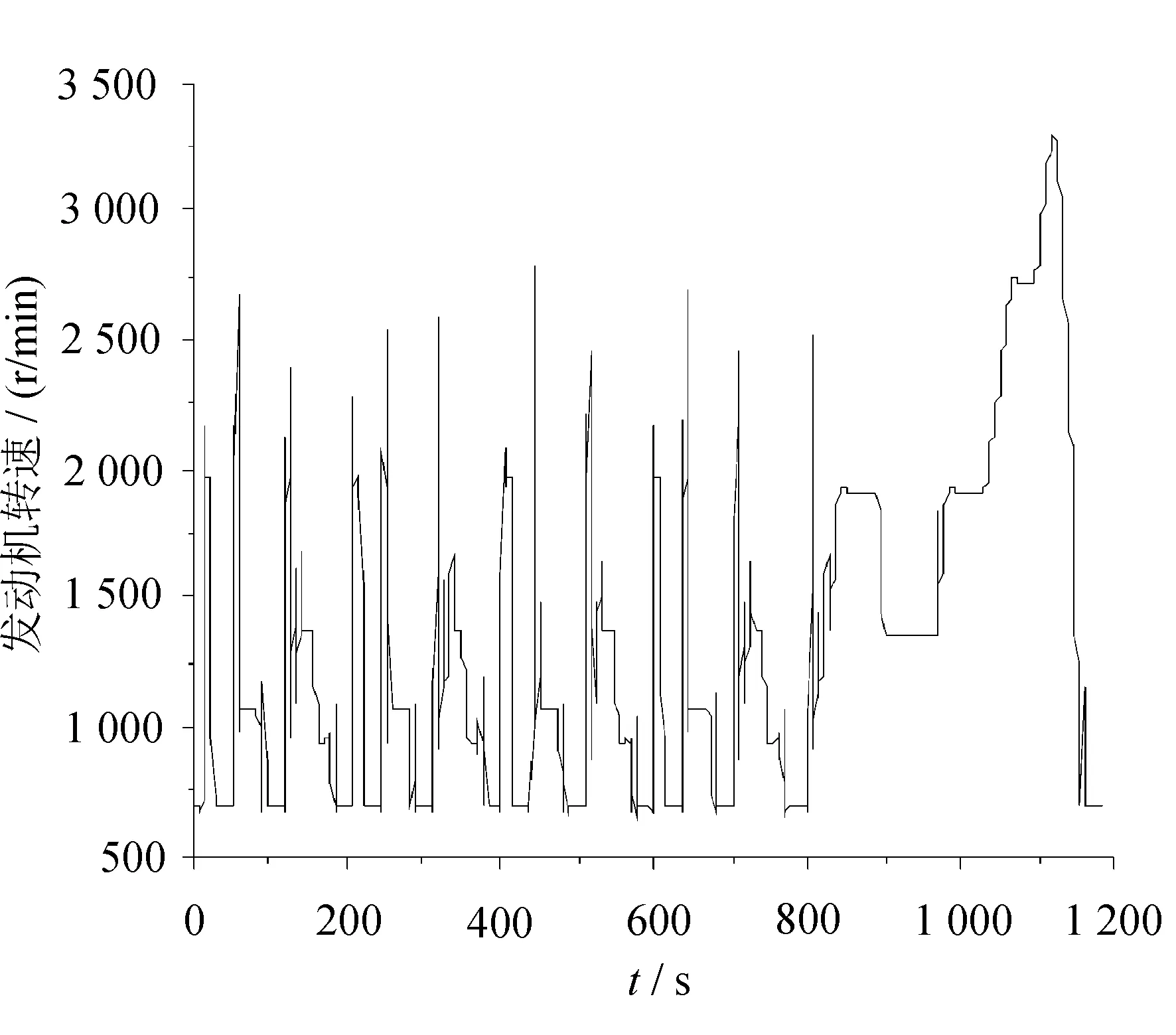
(a) 发动机转速变化曲线

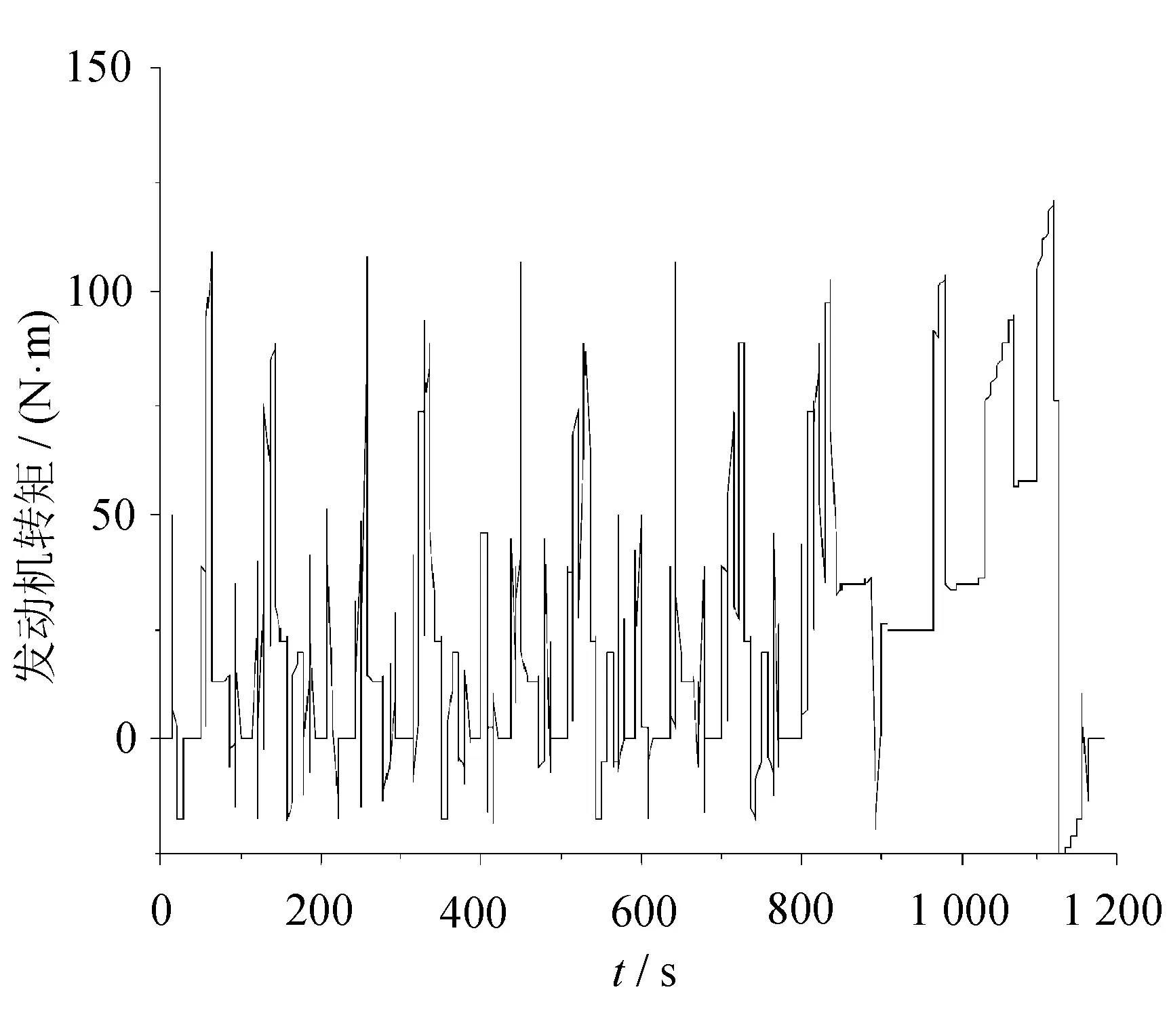
(b) 发动机转矩变化曲线

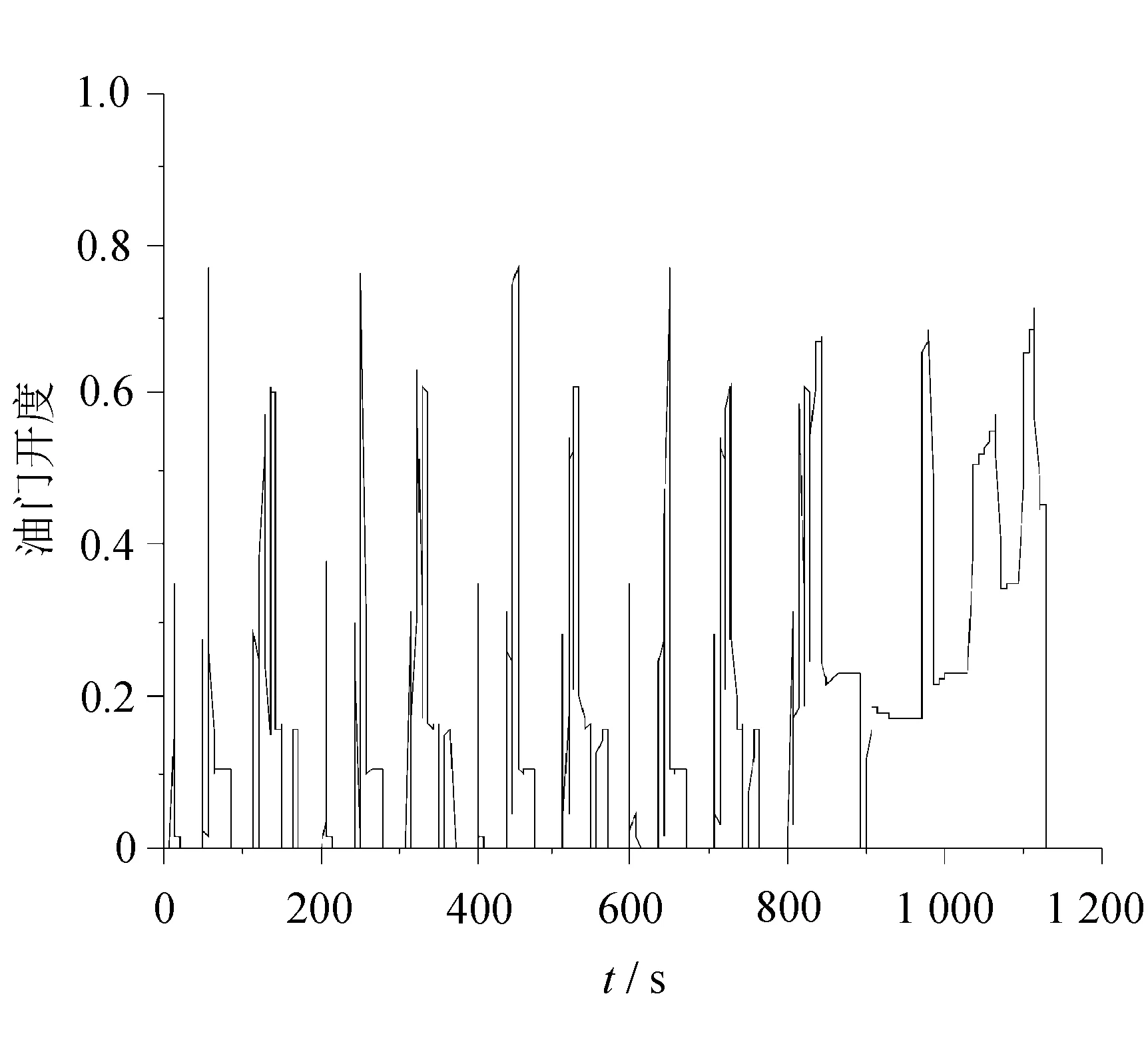
(d) 油门开度变化曲线

4 结 语

根据换挡过程的特性提出运用动态规划理论制定换挡规律的方法，优化出在保证动力性的前提下，具有良好经济性的换挡规律map；在AMEsim和Matlab/Simulink中搭建离线联合实验仿真平台；为了加快软件开发进程，将整个控制方案下载到dSPACE主机中，做了基于dSPACE的快速控制原型硬件实验。实验结果与离线仿真一致，说明该方案具有良好的实时性和有效性。