改进Harris角点检测算法

韩松奇, 于微波， 杨宏涛， 王世程

(长春工业大学 电气与电子工程学院， 吉林 长春 130012)

0 引 言

角点是图像的重要局部特征，它既保留了图像中的特征信息,又同时有效地减少了信息数据量。角点检测在图像匹配、光流计算、运动估计、形状分析、相机标定、视觉的定位和测量等方面都有重要的应用[1]。

当前的角点检测技术可以分为两类：第一类是基于图像边缘信息，此方法经过三个步骤才能完成，分别为图像预分割、轮廓链码提取及角点检测，如基于边界小波变换的角点检测[2]、基于边界链码的角点检测[3]等；第二类是基于图像灰度信息，此方法主要通过计算曲率及梯度通过计算边缘曲率来判断角点的存在性，如Harris算法和SUSAN算法等。在实际应用中，前者角点过于依赖边缘信息，当被检测目标局部发生变化，可能会导致角点提取失败，所以应用范围有限；后者可能会出现漏检角点和伪角点等情况，其中Harris算法应用最为广泛，但是会出现精度不高、运算量大等问题。

针对Harris算法的不足，众多学者对经典的Harris算法进行了改进。毛雁明等[4]提出双阈值算法，解决了不易设置阈值的问题。赵萌等[5]提出了一种自适应参数算法，解决了因高斯参数固定导致的角点检测不准确的问题。李鹏程等[6]提出了一种优化算法，解决了原始算法实时性不好的问题。以上改进算法取得了一定成效，但是依旧存在检测精度低和实时性差的问题。文中提出了一种改进算法，首先采用B样条函数替代高斯窗口函数，以提高角点定位精度，再对角点进行预筛选，以提高算法的实时性，最后在非极性最大值时，采用阈值自适应方法以提高算法的自适应性。

1 Harris角点检测算法原理

Harris角点检测算法是由Harris等[7]提出的，其是在原有Moravec算法的基础上改进的一种基于信号的点特征提取算法。Harris算法使用微分运算和自相关矩阵来进行角点检测，具有运算简单、提取的角点特征均匀合理、性能稳定等特点。利用微分算子能够反映像素点在任意方向上的灰度变化这一特点，有效地辨别角点和边缘点，假设图像像素点(x,y)的灰度为I(x,y)，以像素点为中心的窗口沿x和y方向分别移动u和v的灰度强度变化的表达式为：

(1)

式中：Eu,v----窗口灰度值；

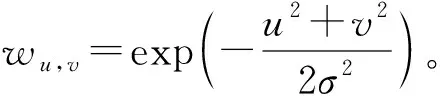
为有效提高抗干扰能力，对于微小的位移，可以忽略无穷小项O(u2,v2)，有

(2)

将Eu,v(x,y)化为二次型有

(3)

其中

称M为像素点的自相关矩阵。

则角点响应函数CRF(Corner Response Function)：

CRF=det(M)-k(tr(M))2

式中：det(M)----自相关矩阵M的行列式；

tr(M)----自相关矩阵M的迹；

k----一般取0.04～0.06。

当某像素点的角点响应函数在其邻域内为最大值，同时大于设定的阈值时，则该像素点为角点。

2 Harris算法的改进

Harris算法充分利用了角点的特征，适用于角点数目多且光源复杂的图像，但存在以下不足：第一，Harris算法采用可调窗口的高斯函数对图像进行图像平滑处理，但实际应用中高斯窗口的大小不易控制,当高斯窗口过小时，会有较多的伪角点产生；高斯窗口过大时，会使得角点位置出现偏移现象。第二，Harris算法的检测效果过于依赖于阈值的设定,当设定的阈值较小时，会出现大量的伪角点；当设定阈值较大时，会有许多漏检角点。为此，文中从以下三个方面进行改进：

1)针对高斯窗口大小不易选择，角点定位不准确等问题，采用B样条函数[8]替代原算法中的高斯窗口函数，提高角点定位精度。

2)针对Harris算法的运算量较大、运行时间较长等现象，对角点进行预筛选处理，以图像像素点为中心与其邻域8个点的像素灰度值进行比较，剔除了大量的伪角点，提高了算法的实时性。

3)针对提取角点时所用的阈值是手动设定、调试复杂等问题,采用自适应阈值的方法，提高自适应能力。

2.1 B样条函数及其模板

利用B样条函数具有局部性及仿射不变性等特性，将高斯窗口函数由B样条函数替代。

N次B样条函数定义为

(4)

式中：u(x)----阶跃函数；

n----B样条函数的阶数。

当n增加时，平滑效果会更好，且过滤效果更强，但是会产生延迟，且容易失去边界信息；当n减少时，图片细节能很好地保存下来，但去噪能力降低。

离散式数字图像滤波公式为：

(5)

式中：f(i,j)----像素(i,j)处图像灰度值；

Bk×l(x-i,y-j)----B样条滤波算子。

滤波模板通常是一个(2m+1)×(2m+1)的矩阵，其中m=1,2,…,n。通过实验证明，能抑制噪音的最佳平滑滤波器是三阶B样条函数[9]。所以文中采用三阶B样条函数，取k=l=n=3，得到B样条函数的3×3滤波模板，可以表示为

(6)

由B样条函数局部性质，n次样条函数空间的二维结构为：

(7)

其中，Bn(x)可以表示为

(8)

经过计算，得到B样条函数在x和y方向上的微分模板：

(9)

2.2 获取候选角点

设中心点像素的灰度值与邻域任意一个像素点灰度值差的绝对值为Δ，设阈值为t，假如Δ≤t，则认为中心点与该点相似，同理可以判断中心点与其邻域内其它点是否相似。本改进算法采用3×3的检测窗口，需要考虑中心点与其8邻域内像素点的相似度。设中心点与其邻域内的点相似的个数为N(i,j)。

-1≤x≤1, -1≤y≤1,x≠0,y≠0

(10)

其中

根据上述可知，0≤N(i,j)≤8，下面对N(i,j)进行分析。

不符合候选点的情况如图1所示。

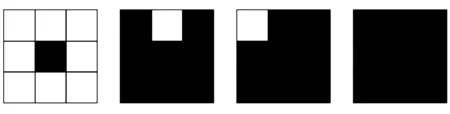
(a) (b) (c) (d)

1)N(i,j)=0，表示中心点邻域内没有与之相似的点，所以该中心点为孤立点或噪声点，不能作为候选点，见图1(a)；

2)N(i,j)=7，有两种情况，分别见图1(b)和(c)，图1(b)可能的角点应该是中心点的正上方的那个点，图1(c)可能的角点应该是中心点左上方的那个点，因此这种情况不能成为候选点；

3)N(i,j)=8，表示中心点邻域内的8个点全是相似点，不能成为候选点，见图1(d)；

4)1≤N(i,j)≤6，这种情况下中心点都可能为角点，因此可成为候选点，如图2所示。

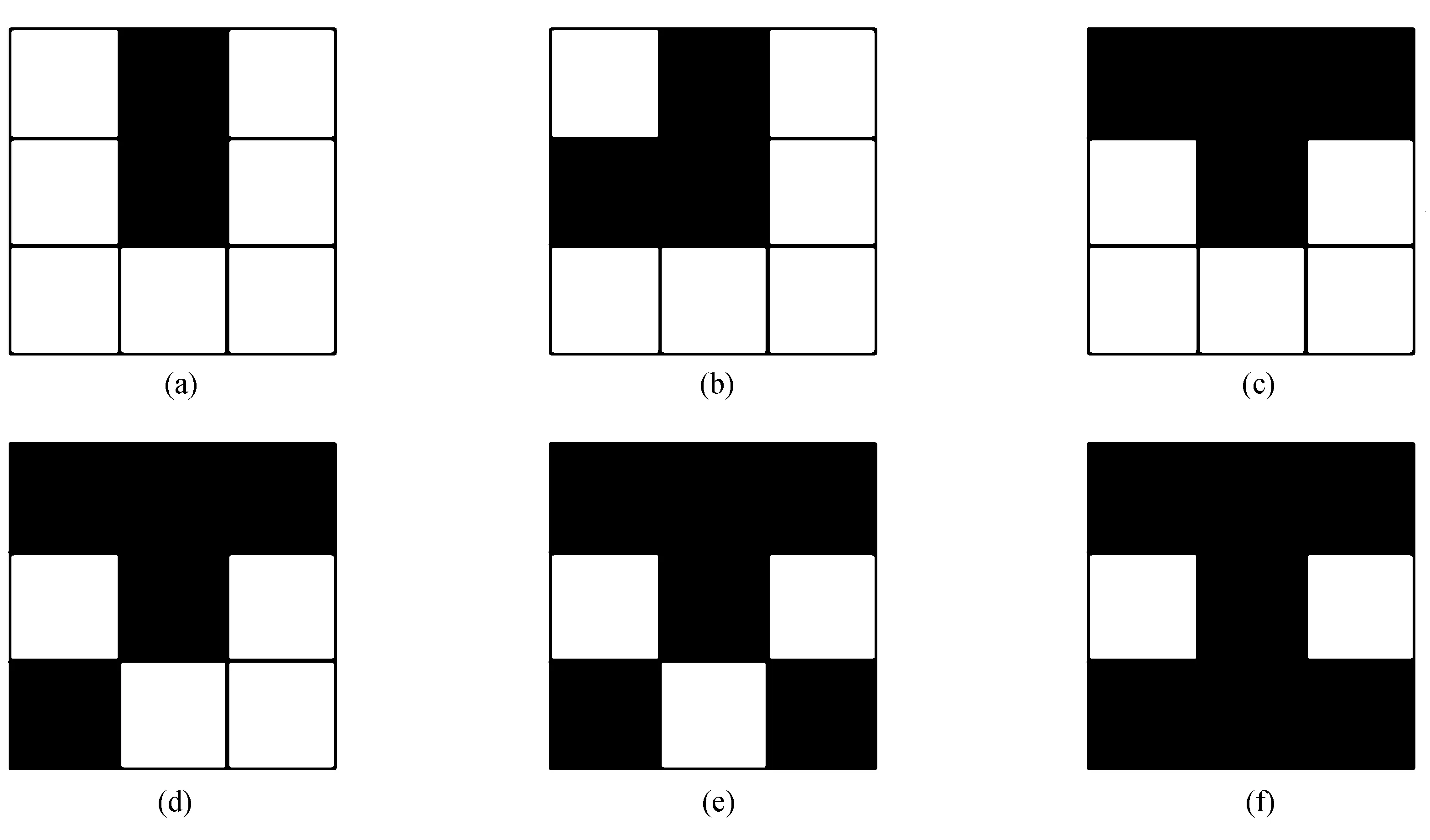
图2 符合候选角点的情况

2.3 自适应阈值

采用Harris算法对一副图片进行角点提取时，需要通过设定一个固定阈值进行不断调试，可以得到比较好的结果，但是所设置的阈值并不一定对其他图片都适用，还要重新调试。考虑算法的通用性，需要算法本身有能力计算出合适的阈值。

本算法将阈值设定为角点响应函数最大值的p倍，即：T=p×CRFmax。

其中p取经验值[0.005,0.015]时，基本会检测出所有的角点，同时检测到伪角点的数目较少。

3 实验结果及分析

为了验证文中改进算法的有效性，使用标准图像库中的 “积木”图片(大小为256×256)进行实验，分别采用Harris算法和改进后的Harris算法对图片进行角点检测，实验结果如图3所示。

实验数据结果对比见表1。

表1 实验数据结果对比

可以看出,原始的Harris算法会检测出很多伪角点，同时运行时间很长。而改进的Harris算法大大降低了程序的运行时间，从0.557 s缩减到0.153 s，效率提升了30%；检测到的准确角点更多，伪角点数更少，从13个缩减到3个，准确率提高了23%。

4 结 语

针对Harris角点检测算法运行时间长和精确度低等不足，提出了一种改进的Harris算法。首先采用B样条函数替代高斯窗口函数，提高角点定位精度，再对角点进行预处理，选出候选角点，最后在非极大值抑制时采用自适应阈值，提高算法的自适应性。实验表明，改进的Harris算法不仅大大缩减了运算时间，提高了实时性，而且还提高了角点检测的准确性，减少了伪角点数。