基于外来物种的生物系统滑模控制器设计

张巧玲, 陆海霞, 张 翼

(1.宿迁学院 文理学院, 江苏 宿迁 223800； 2.沈阳工业大学 理学院, 辽宁 沈阳 110870)

0 引 言

数学与我们的生活密切相关。随着社会经济的不断发展,人们不断探索数学对生态学的研究[1-2],从而对生物种群的数学研究越来越细化[3-4]。文中是关于美国白蛾的研究，美国白蛾[Hyphantria cunea(Drury)]是危害园林植物的一种重要检疫害虫,作为外来物种入侵我国,造成了经济与环境的双重损失[5]。滑模变结构控制是50年代末由前苏联学者S.V.Emelyanov 等最先提出,后经进一步研究而发展起来的一类非线性控制系统综合方法[6-7]。最早起源于对继电器和 Bang-Bang 控制的研究。由于系统在滑动平面上的滑模运动对系统的参数摄动、外界参数的变化、系统不确定模态和模型不确定具有不变性,也就是完全鲁棒性,滑模变结构控制引起人们的极大兴趣[8]。

文中主要做了以下工作,首先,研究对象为入侵物种美国白蛾在某自治生态系统的引入或逸出密度,以及本地物种经历入侵过程中的引入或逸出密度。实际上,考虑物种引入或逸出密度是考察物种是否在该生态系统中占据稳定的生态位,形成完整的生物链的重要依据。其次,将滑模变结构控制方法引入生物数学。最后,通过对控制器仿真效果的比较,揭示相应的生物学意义和实际应用价值。

1 系统描述

考虑如下具有外来物种入侵的系统模型：

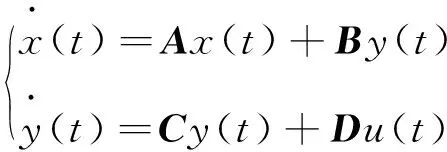
(1)

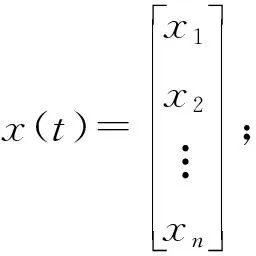
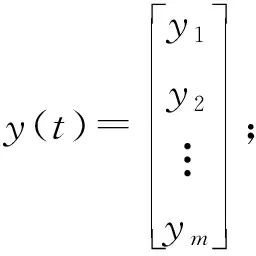
u(t)----系统控制输入；

A,B,C,D----相容维数的参数矩阵。

设计切换函数为：

S(x)=Θx

(2)

式中：Θ----相容维数的待定矩阵,且满足Θ[B(-C)-1D]>0。

定义Lyapunov函数为:

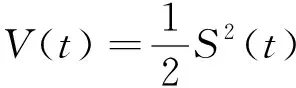
2 滑模控制器的设计

2.1 常值切换控制

定理1对于系统(1),设计切换函数(2),设计控制律为：

u=-Ksgn(S)

(3)

其中,K>|[ΘB(-C)-1D]-1ΘAx|,sgn为符号函数,|·|为绝对值函数,则系统(1)渐近稳定。

SΘAx+SΘ[B(-C)-1D]u=

SΘAx-SΘ[B(-C)-1D]Ksgn(S)=

SΘAx-Θ[B(-C)-1D]K|S|<

SΘAx-|SΘAx|<0

2.2 加权积分型增益的滑模控制器

定理2 对于系统(1),设计切换函数(2),设计控制律为：

u=ueq+ud

(4)

其中

ueq=-[ΘB(-C)-1D]-1ΘAx

ud=-Kw|ρ|sgn(S),Kw>0

则系统(1)渐近稳定。

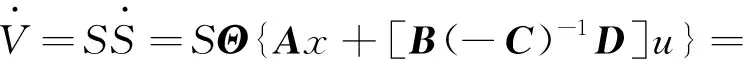
SΘ{Ax+[B(-C)-1D][-[ΘB(-C)-1D]-1ΘAx-Kw|ρ|sgn(S)]}=

SΘAx+SΘ[B(-C)-1D](-Kw|ρ|sgn(S))-SΘAx=

-KwSΘB(-C)-1D|ρ|sgn(S)=-KwΘB(-C)-1D|ρ||S|<0

式(3)为常规的滑模控制器,为了保证系统的鲁棒性,控制器的增益必须足够大,这就不可避免地产生抖振。当不在滑动模态阶段时,S(t)值较大,S(t)的积分值也较大,造成切换项的增益也较大,抖振严重。为此,式(4)给出了一种具有积分形式增益的滑模控制器,又进一步在积分项中引入负的权值Kf,有效避免了当系统不在滑动模态阶段时切换项增益的增大。

3 仿 真

根据对美国白蛾生物属性的调研,取适当参数如下:

n=2

m=2

则x=(x1,x2)T,分别代表绿叶类白蛾喜食的植物在某生态系统的引入或逸出密度和以蛹蛾为食的鸟类在生态系统的引入或逸出密度。y=(y1,y2)T,分别代表幼虫时期与成虫时期的美国白蛾在生态系统的引入或逸出密度。

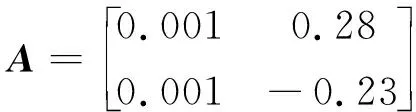
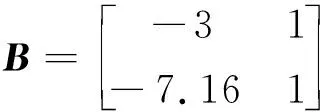
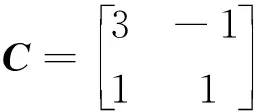
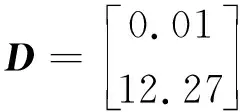
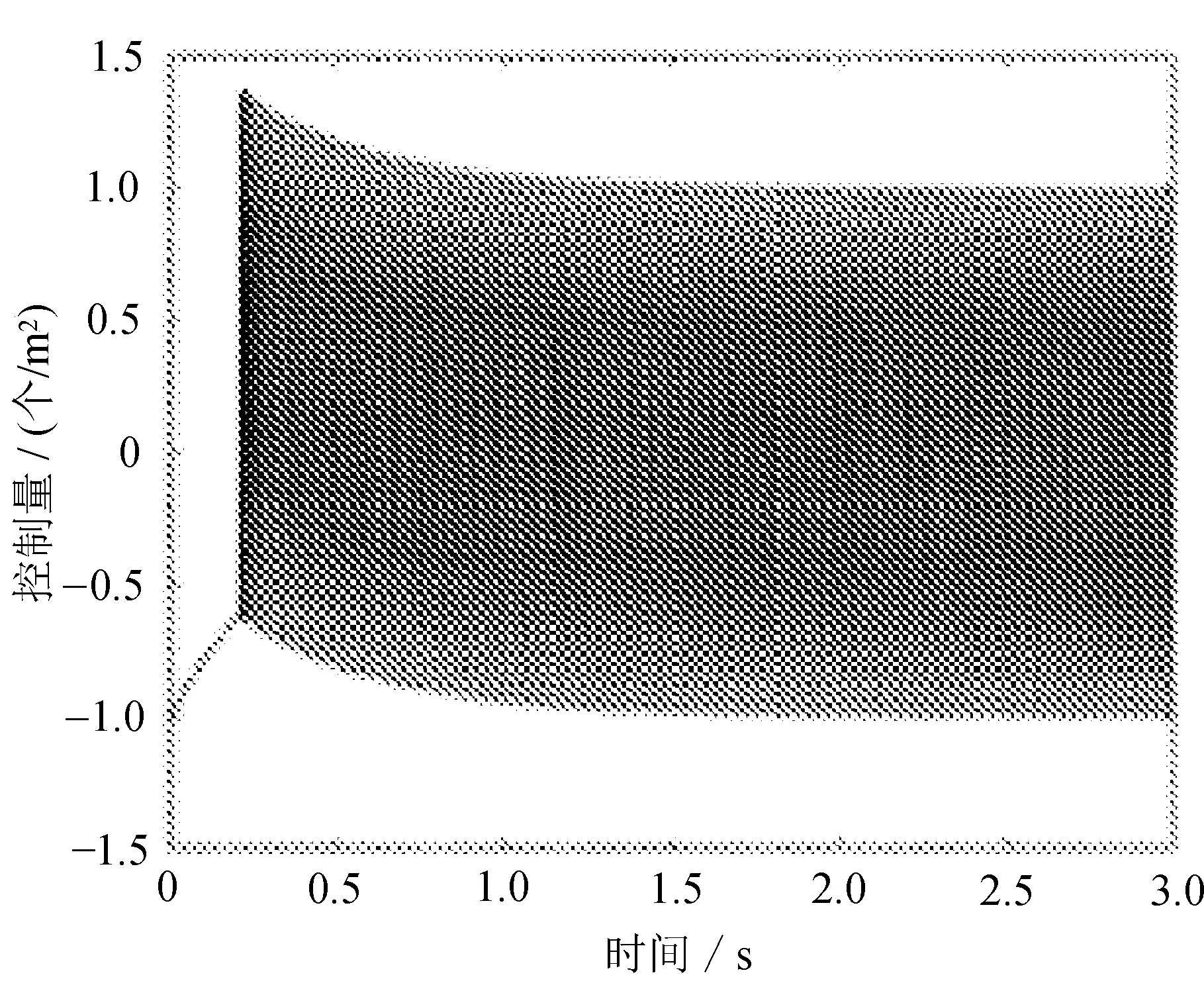
(a) 控制输入(3)的状态

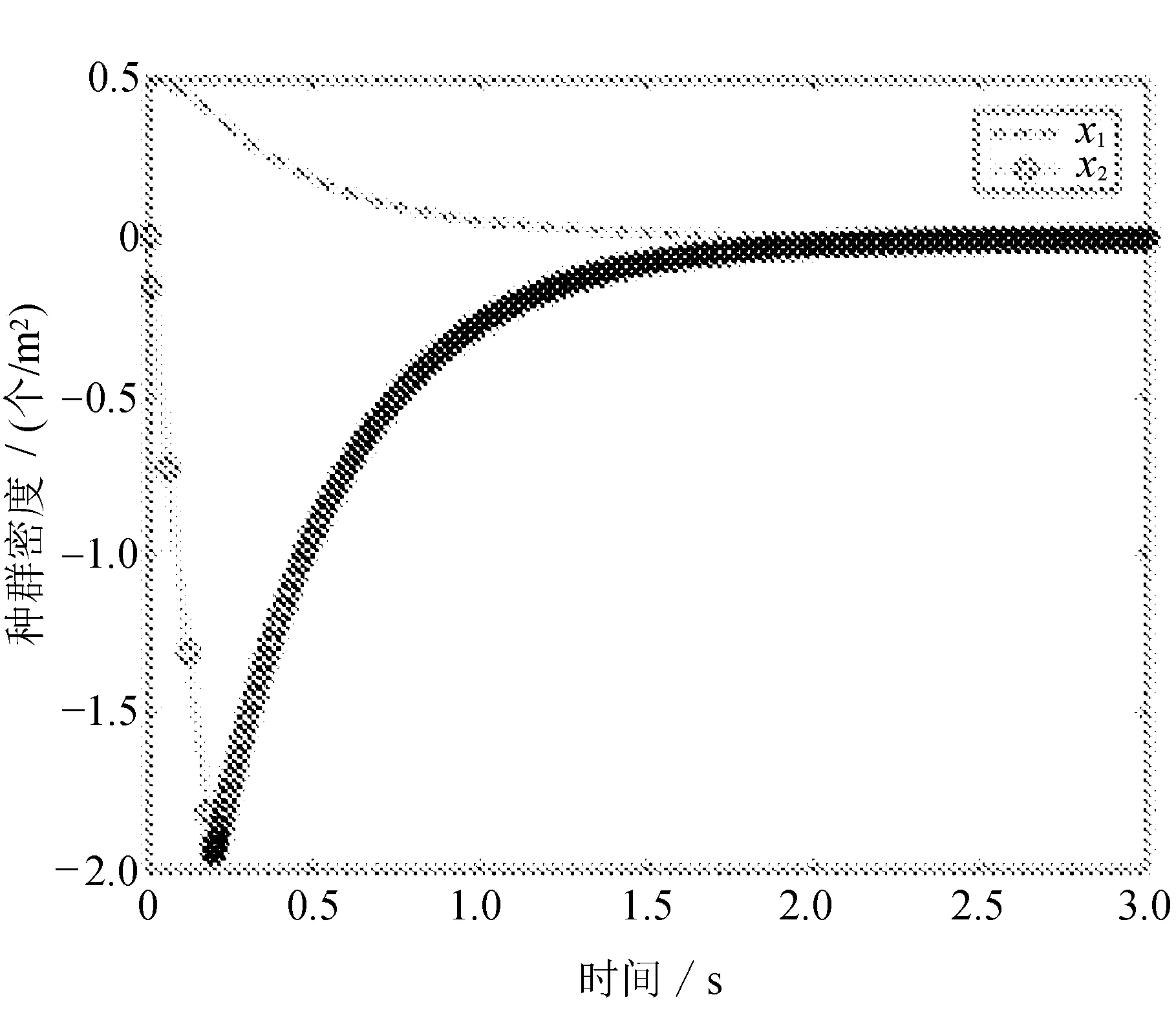
(b) 控制输入(3)下的x1,x2的状态

(c) 控制输入(3)下的y1,y2的状态

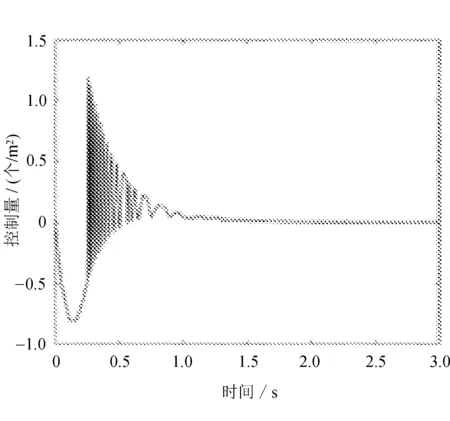
(a) 控制输入(4)的状态

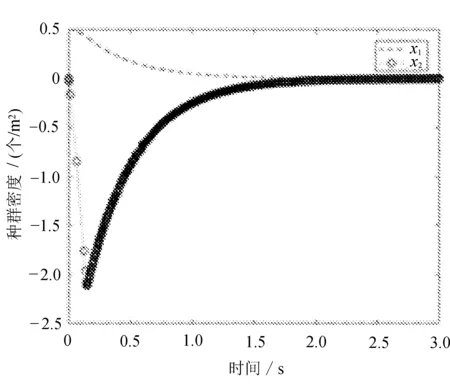
(b) 控制输入(4)下的x1,x2的状态

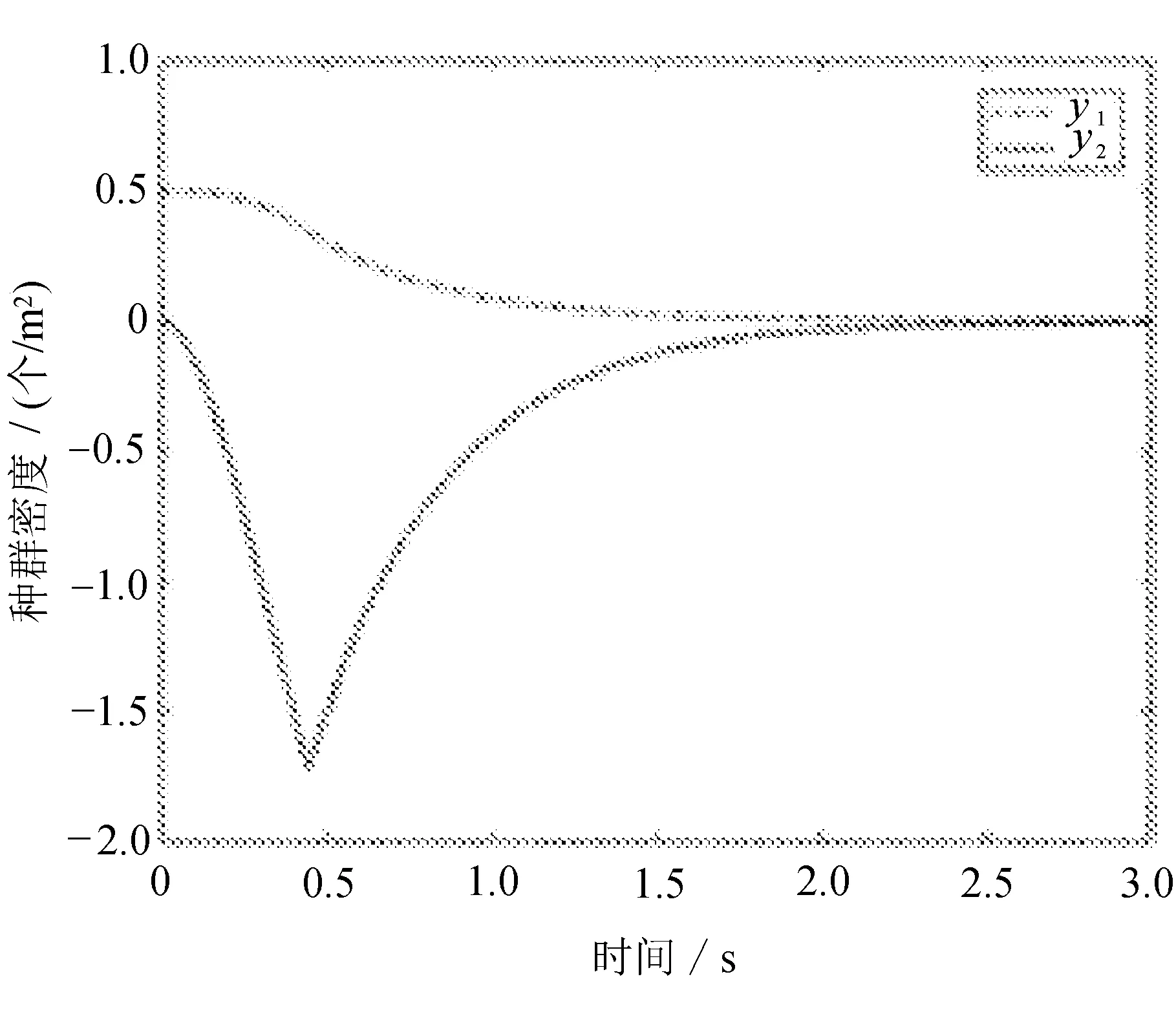
(c) 控制输入(4)下的y1,y2的状态

不同控制器确保滑动运动达到切换面的控制输入信号有所不同,可以明显地看出控制器(4)的输入信号最先趋于稳定。图1和图2说明,控制器均能够使本生态系统的绿叶植物及食蛾鸟类的引入逸出密度变化调节,具体地说,各种控制手段使得白蛾幼虫的逸出率大幅度增加,成虫的引入率有所下降,最终引入或逸出密度趋向于零。可以观察到对抖震的处理效果,控制器(4)较为灵敏。

4 结 语

基于滑模控制理论研究了外来物种入侵下的物种密度波动变化问题。得到以下结论：对于一般的控制器如常值切换控制,由于外界扰动和系统参数变化等因素的影响,会使系统运动偏离滑模面。设计加权积分型增益的滑模控制器，该控制器包含切换函数S的积分的绝对值，并在积分项中使用了积分项的加权值。这样有效地避免了当系统不在滑动模态阶段时切换增益的增大。从应用角度出发，美国白蛾的控制也是各种手段加权的结果，生物防治如周氏啮小蜂寄生防治；化学防治如高射程喷雾机防治、飞机施药防治、喷雾防治、打孔注药防治、树干涂毒环防治；物理防治如人工捕蛾防治、灯光、性诱杀防治、摘除卵块防治、剪除网幕防治、围草诱蛹防治、人工挖蛹防治等。