山区地形实测风非平稳特性和非高斯特性分析

辛亚兵， 刘志文， 邵旭东， 卢山东

(1. 湖南大学 风工程与桥梁工程湖南省重点实验室， 长沙 410082； 2. 现代投资股份有限公司， 长沙 410004)

山区地形风特性具有风速高、非平稳性突出的特点[1-2]，风荷载常常表现为非平稳性，基于传统平稳风速分析不能真实反应风场特性。目前国内外结构设计规范均假设风速为平稳过程，对山区地形风荷载仅建议进行风观测或地形模型风洞实验进行修正[3-4]。因此研究山区地形桥位风场特性对山区高墩大跨桥梁抗风设计具有重要意义。

目前关于实测风非平稳特性和非高斯特性已开展了一些研究。Xu等[5-6]对香港青马大桥实测风速样本采用经验模态法(Empirical Mode Decomposition, EMD)提取时变平均风速，并将概率密度函数、湍流强度、阵风因子、功率谱密度函数计算结果与传统分析方法进行比较，研究结果表明采用EMD法描述非平稳风速较传统分析方法更适合。何旭辉等[7-8]对湖南洞庭湖大桥风雨振实测样本采用小波法提取风速、风向时变均值，并将紊流强度、积分尺度、脉动风谱和概率密度函数等计算结果与传统分析方法进行比较。吴本刚等[9]对高层建筑实测风速采用EMD方法提取时变平均风，并将湍流强度、阵风因子、概率密度分布和风速谱等风特性参数与传统平稳模型进行对比，研究结果表明非平稳风速模型更精确描述高层建筑实测风速数据真实状态。张少峰等[10]对空旷平坦地貌实测强风样本采用EMD法提取时变平均风速，建立非平稳风速模型和平稳风速模型，并将两种模型计算湍流强度、阵风因子、积分尺度、功率谱密度函数的结果进行比较研究。申建红等[11]分别采用小波变换和EMD两种方法非平稳风中时变均值的提取，研究结果表明采用一定层次系数离散正交变换得到较为准确的时变均值。楼文娟等[12]对超高层建筑进行风洞试验，研究建筑表面风压非高斯分布。近年来有学者开始关注山区非平稳风特性研究，如黄国庆等[13]对云南普立大桥实测非平稳强风样本分析了桥梁静风响应和抖振响应，研究结果表明非平稳强风采用传统分析方法会低估桥梁静风响应，采用规范风谱计算抖振响应偏于不安全。综上所述，现有大部分文献未对实测风非平稳和非高斯的定量检验进行系统阐述。

针对赤石特大桥实测强风样本，首先采用ADF法对实测风速样本非平稳性进行了定量检验，利用小波变化法提取非平稳风的时变平均风速，最后对实测风样本脉动风速分别进行平稳风速模型与非平稳风速模型下的高斯特性对比分析。本文研究旨在为定量检验风速样本非平稳性和非高斯性提供依据，为进一步开展山区复杂地形大跨桥梁的抗风性能研究奠定基础。

1 非平稳和非高斯检验方法

1.1 非平稳检验方法

平稳时间序列分为严平稳时间序列和宽平稳时间序列[14]。在实际中往往使用宽平稳概率，其定义为：对时间序列Xt，同时满足式(1)～式(3)则为宽平稳时间序列；若不满足其中一项则为非平稳时间序列[15]

E(Xt)=μt

(1)

(2)

Cov(Xt,Xt+k)=E[(Xt-μ)(Xt+k-μ)]=γk

(3)

式中:E为期望;Cov为协方差;μ为均值常数;σ2为标准差常数;γk为时间差k单变量函数;t为时间参数。

非平稳时间序列检验方法通常分为图形检验和统计量检验。图形检验是通过图形趋势直观进行判断，分为时间序列趋势图检验和自相关函数图检验。统计量检验通过计算统计量进行统计判断，更为准确和重要，分为DF(Dickey Fuller)法和ADF(Augment Dickey Fuller)法。DF检验原理为：假定时间序列Xt的差分ΔXt一阶自回归表达式为

ΔXt=α+δXt-1+μt

(4)

式中:α为截矩;δ为系数;μt为白噪声，统计量t值按普遍最小二乘法估计计算，ADF临界值是显著性水平对应分位点，由显著性水平和样本容量从ADF临界值表查得。实际检验时将t值与DF临界值比较，当t小于临界值，则拒绝零假设，δ=0，认为时间序列Xt不存在单位根，是平稳的；反之为非平稳。ADF检验与DF检验两者原理相同，并对DF检验进行了扩充，适用于高阶自回归过程或者随机误差项并非是白噪声的情况。ADF检验有以下三种模型

模型1：

(5)

模型2：

(6)

模型3：

(7)

式中:模型2在模型1基础上增加了常数项α;模型3在模型2基础上增加了趋势项βt;i为参数。具体检验时从模型3开始，然后模型2、模型1，何时检验拒绝零假设，不存在零假设为平稳序列，何时检验停止，否则继续检验直到检验至模型1为止。

1.2 非高斯性检验方法

风速时间序列非高斯性可以根据概率密度函数曲线进行直观检验，具体方法是做出风速时程概率密度曲线，并与标准正态分布曲线对比，从直观上判断风速信号是否符合高斯性。概率密度p(u)表达式为

(8)

式中:u为风速；σu为风速标准差。

根据统计学原理[16]，采用高阶统计量进行风速时间序列非高斯性统计定量检验。斜度值是衡量随机时间序列分布偏离对称分布的程度，斜度值越大越偏离对称分布。峰态值是衡量时间序列分布尖削程度，峰态值越大分布越尖削。因此时间序列的非高斯性取决于一定斜度值和峰度值的范围。假设一组非高斯信号Ut，不能满足中心极限定理，需要3、4阶中心距统计量进行描述幅域分布。3、4阶中心距分别称为斜度值Usk和峰态值Uku，表达式为

(9)

(10)

|Usk|>0.2

(11)

|Uku|>3.5

(12)

2 小波变换法

2.1 非平稳风速模型

根据Gramer定理，非平稳风速时程U(t)可以分解为一个确定性时变平均风速和平稳随机脉动风速，其表达式为

(13)

2.2 小波变换原理

综合何旭辉等和申建立等的研究成果，采用小波变换提取实测非平稳风速中时变平均风速。小波变换WT可表示为

(14)

式中：x(t)为待分析信号；ψ(t)基本小波函数；a为分析尺度；τ为平移位移。其中ψa,τ(t)>0,a>0。

将小波变换参数a，τ做离散化，其离散小波函数表示为

(15)

式中：j=0,1,2，…；k=0,1,2，…。则离散小波变换可表示为

(16)

离散小波重构信号表达式为

(17)

式中：c为与信号无关的常数。由于正交离散小波变换可以消除信息冗余，采用一阶正交离散小波变换法提取实测非平稳风样本时变平均风速。

3 工程背景

湖南赤石特大桥为四塔双索面预应力混凝土斜拉桥，其主跨为165 m+3×380 m+165 m四塔五跨预应力混凝土双索面斜拉桥，主塔高达285.6 m，最高主塔桥面至承台顶高185.7 m。桥址为山区峡谷地形，峡谷呈东北-西南走向，桥位北方为谷口，南方为开阔口，东西两边为陡峭山体，最大相对高差约210 m。图1为赤石特大桥桥位地形图。赤石特大桥风观测系统由风速仪、数据采集系统、数据传输系统、数据储存和处理终端组成。风观测系统在位于峡谷中间 6、7号主塔塔顶分别布置一个二维风速仪，在6、7号主塔两侧桥面分别布置一个二维风速仪和一个三维超声风速仪，桥面风速仪随施工进度调整观测点位置。图2为赤石特大桥风速仪安装照片。

图1 赤石特大桥桥位地形图Fig.1 Topographic map at the Chishi bridge site

图2 桥面上三维风速仪Fig.2 Three dimensional anemometer of Chishi bridge

4 风速非平稳、非高斯分析

4.1 实测山区风样本

笔者等结合赤石大桥施工进度对桥位风特性进行了为期两年多的现场实测。在大量实测数据基础上，选取平均风速达到10 m/s的强风(工程规定强风风速为10.8～13.8 m/s)作为样本。利用矢量法对风速样本进行处理，得到顺风向、横风向和竖风向的实测风速。以6号塔三维超声风速仪实测风速为例，采样频率为10 Hz，本文仅研究顺风向实测风速。2014年5月14日在22:00～23:00时段实测风速见图4(a)，为山区常见风速样本(以下称为样本1)； 2014年7月3日在07:00～08:00时段实测风速见图4(b)，从图中可以看出风速有明显的突变过程(以下称为样本2)，为山区中典型突变风样本。由图4可以看出突变风样本与山区常见风样本风速变化趋势有明显区别。在2013年～2014年观测期间多次观测到此类突变风天气，这些现象表明桥位处风速较大，且突变风较常出现。

4.2 非平稳性检验

提取实测风速数据保存至文本文件，按ADF检验方法编制Matlab程序进行检验，显著性水平为0.05，表1给出了非平稳性检验结果。由表1可以看出，样本1按从模型3～模型1顺序检验，统计量t值均大于ADF临界值，从而不能拒绝零假设，检验结果为非平稳；样本2按从模型3～模型1顺序检验，统计量t值均大于ADF临界值，从而不能拒绝零假设，检验结果为非平稳。

表1 典型风速样本非平稳检验结果Tab.1 Result of non-stationary test for typical wind samples

4.3 时变平均风速提取

选取提取精度较高的Daubechies(DB10)小波函数进行时变平均风速的提取，对实测风速进行一阶正交离散小波变换，如图3所示。小波变换时最佳分解层数按方俊研究中的方法确定，分解层数取12层，提取最大层近似系数即为时变平均风速。图3(a)～图3(c)为近似系数a1～a12，近似系数a12为时变平均风速。图4为样本1、样本2时变平均风速与10 min常值平均风速计算结果比较。由图4(a)可知，时变平均风速最大值为11.312 m/s，常值平均风速最大值为10.225 m/s。由图4(b)可知，时变平均风速最大值为12.938 m/s，常值平均风速最大值为10.887 m/s。综合样本1、样本2计算结果，时变平均风速最大值比10 min常值最大平均风速分别提高10.63%和18.84%，由此可见对这种大风天气只是做10 min平均风速处理会因其平均后风速比较小而被忽视。

(a) 近似项a1～a4

(b) 近似项a5～a8

(c) 近似项a9～a12图3 实测风速小波分析Fig.3 Wavelet analysis for wind speeds measured in mountainous terrain

4.4 脉动风速

对三维超声测风仪实测的风速数据进行预处理，剔除无效和野点数据，然后提取脉动风速。图5为样本1、样本2的非平稳风速模型和平稳风模型计算脉动风速计算结果。由图5(a)可以得到样本1非平稳风速模型计算的脉动风速时程和平稳风速模型计算脉动风速时程均较接近平稳分布；由图5(b)可以得到样本2非平稳风速模型计算脉动风速与平稳风速模型计算脉动风速时程分布不平稳。

4.5 非高斯性检验

按照式(8)计算了样本1、样本2非平稳风速模型和平稳风速模型的脉动风速概率密度，如图6所示。由图6(a)可知，样本1由非平稳风速模型和平稳风速模型得到的脉动风速概率密度均接近高斯分布。由图6(b)可知，样本2由非平稳风速模型和平稳风速模型得到的脉动风速概率密度均偏离高斯分布。

按照式(9)、式(10)计算了脉动风速时程对应的高阶统计量，表2给出了样本1、样本2脉动风速时程高阶统计量计算结果，并按照式(11)、式(12)标准进行了高斯性检验。由表2可以看出，样本1由非平稳风速模型计算的脉动风速斜度值绝对值小于0.2，峰态值绝对值小于3.5，检验为高斯；由平稳风速模型计算脉动风速斜度值绝对值小于0.2，峰态值绝对值接近3.5，检验为接近高斯。样本2由非平稳风速模型计算的脉动风速斜度值绝对值大于0.2，峰态值绝对值大于3.5，检验为非高斯；由平稳风速模型计算脉动风速斜度值绝对值大于0.2，峰态值绝对值大于3.5，检验为非高斯。

表2 脉动风时程高阶统计矩计算值Tab.2 Values of high order statistical moments of fluctuating winds

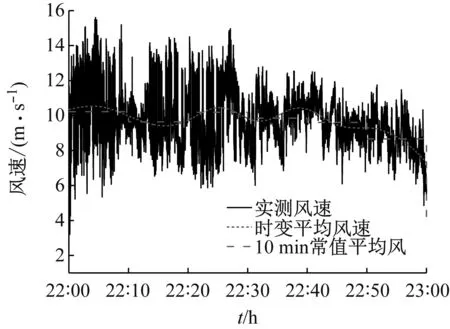
(a) 样本1

(b) 样本2图4 时变平均风速和10 min常值平均风速计算结果比较Fig.4 Comparison time varying speeds with 10 min mean speeds

(a) 样本1

(b) 样本2图5 非平稳风速模型和平稳风速模型脉动风速计算结果比较Fig.5 Comparison of fluctuating winds of non-stationary wind model and stationary wind model

(a) 样本1

(b) 样本2图6 脉动风速概率密度分布Fig.6 Probability distributions of fluctuating wind speeds

5 结 论

(1) 通过实测表明，山区桥位出现突变性质的强风。采用统计学ADF法定量检验了实测风样本的非平稳性。

(2) 对于山区常见非平稳风样本，采用非平稳风速模型和平稳风速模型计算脉动风速接近高斯分布；对于山区突变风样本，采用非平稳风速模型和平稳风速模型计算脉动风速为非高斯分布。

(3) 采用小波法提取的非平稳风样本时变平均风速最大值比10 min常值平均风速最大值分别提高10.63%和18.84%，对这种大风天气只是做10 min平均风速处理会因其平均后风速比较小而被忽视。

限于篇幅，本文选取典型山区常见风样本和突变风样本为例分析非平稳特性和非高斯性特性，山区风特性需要采用更多风样本进行分析，山区突变风对桥梁风致振动响应有待于深入研究。