基于动态插值自适应方法的时变轴系纵向振动主动控制

郑洪波, 覃 会, 胡 芳， 张志谊,3

(1.上海交通大学 机械工程与动力学院，上海 200240； 2. 武汉理工大学 材料科学与工程学院，武汉 430070； 3.上海交通大学 高新船舶与深海开发装备协同创新中心，上海 200240)

对于海洋船舶而言，螺旋桨脉动力会通过轴承引起船体结构振动和水下声辐射。除转向等特殊情况之外，螺旋桨受到的纵向脉动力远大于其它方向的脉动力，纵向振动远大于横向振动，所以控制推力轴承的纵向振动向船体的传递，能够有效减小船体结构振动和声辐射[1]。现有的振动控制研究主要包括被动和主动两种控制方法，如动力吸振器和共振变换器[2-4]。一些主动控制方法如速度反馈控制和最优控制也用来抑制振动从轴系传递到船体[5-8]。在这些研究中，轴系被视为一个时不变系统。然而研究表明，推进轴系的动态特性会随着转速的变化而变化[9-10]，这是由推力轴承油膜纵向刚度会随转速变化导致的，所以在设计控制方案时，必须考虑系统的时变动态特性。

文献[11]提出一种自适应反馈控制策略，通过调整反馈增益来补偿大相位误差，从而避免了时变系统的辨识,但是这种方法仅对已知的周期激励有效，并且收敛速度较慢。文献[12]提出自增益调度H∞控制方法，设计出一个时变的H∞控制器，这种控制方法是基于可获得的参数化系统模型,而实际上很难通过系统辨识的方法得到轴系参数化模型。文献[13]提出用切换控制结构，针对不同时变参数下的系统设计出一个模型参考控制器集，控制过程中根据系统特性的变化进行控制器切换，这种方法要求系统必须可控，辨识出的子系统传递矩阵严格正则并且满秩，系统离散时间状态空间矩阵需要满足相应的关系方程。

本文针对动态特性时变的推进轴系，提出一种动态插值自适应控制方法，利用动态插值算法来更新补偿器，补偿系统动态特性的变化，并根据最小均方算法最小化误差信号。利用这种控制方法进行数值仿真，并与无插值自适应控制时的系统响应进行对比，检验控制方法对时变系统振动的抑制效果。

1 参数时变推进轴系统模型

为了模拟时变轴系的纵向振动特性，建立如图1所示的振动模型，其中螺旋桨等效为有阻尼弹簧振子(图中M1,k1,c1)，轴采用弹性杆模拟，推力轴承采用集中质量M2代替，两者用弹簧和阻尼器(黏性阻尼)连接，并且刚度k2[n(t)]随转速n(t)变化。推力轴承与刚性基础之间通过弹簧和线阻尼器(黏性阻尼)连接，纵振简化模型参数如表1所示。

表1 纵振模型参数Tab.1 Parameters of the longitudinal vibration model

图1 轴系纵向振动模型Fig.1 Vibration model of the shafting system

两端自由的均质杆的纵向振动可以由二阶非齐次偏微分方程描述[14]

(1)

自由端处杆的应力为零，相应的边界条件为

(2)

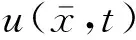
(3)

式中：ω为激励力频率。轴的纵向振动固有频率和振型满足下列特征方程

(4)

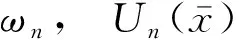
对于两端自由的轴，固有频率和振型为

n≥0

(5)

根据振型叠加法，纵向振幅可以表示成无穷多个主振型的线性组合，即

(6)

将式(6)代入式(3)，得

n≥0

(7)

由式(4)和式(7)，可以得出

n≥0

(8)

(Kn-Mnω2)cn=Fn

(9)

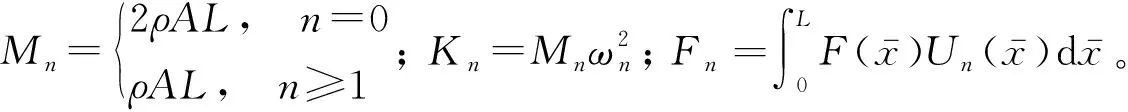
由式(9)可以求出cn。将cn代入式(6)，得到轴的纵振幅值

(10)

(11)

根据式(11)，如果取纵向振动的前五阶主振型，杆端点的原点和跨点频响函数可近似为

(12)

将图1所示的模型分为三个部分，如图2所示。

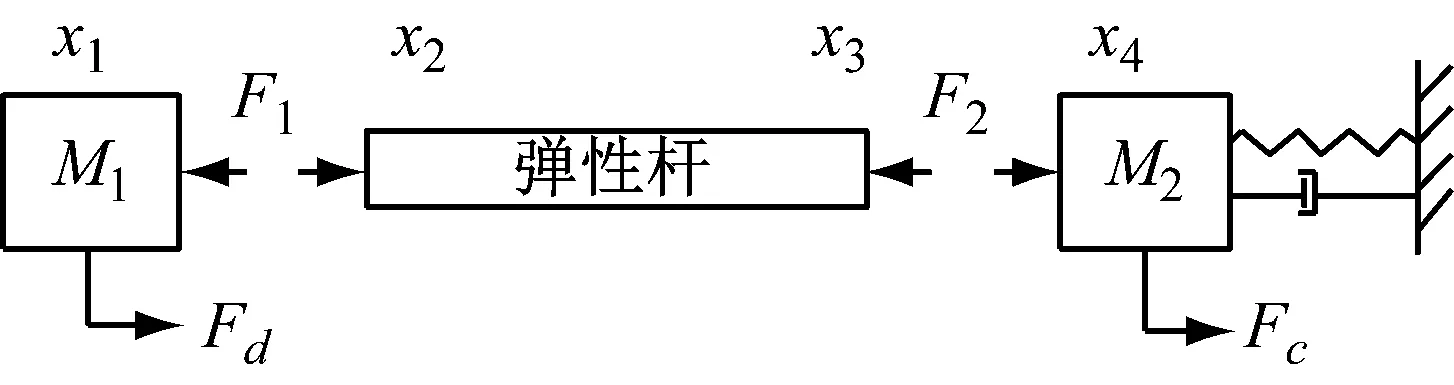
图2 模型分解与分析Fig.2 Model decomposition and analysis

M1的载荷-位移方程

(13)

弹性轴的矩阵方程

(14)

M2的载荷-位移方程

(15)

式中：j为复数的虚部。

联结处力平衡方程

(16)

联立式(13)～式(16)可得到系统位移与外力的关系方程

(17)

在矩阵方程式(17)中，令Fd=0求控制通道模型，再令Fc=0求干扰通道模型

当推力轴承刚度取不同值时，控制通道Hc的幅值和相位曲线图3所示，由图可知，纵向振动固有频率会随着推力轴承刚度的增加而增加，并且第四阶固有频率变化范围为136.7～148.7 Hz，第五阶固有频率的变化范围为207.8～226.4 Hz，最大频率偏移18.6 Hz，最大相位误差172.5°。

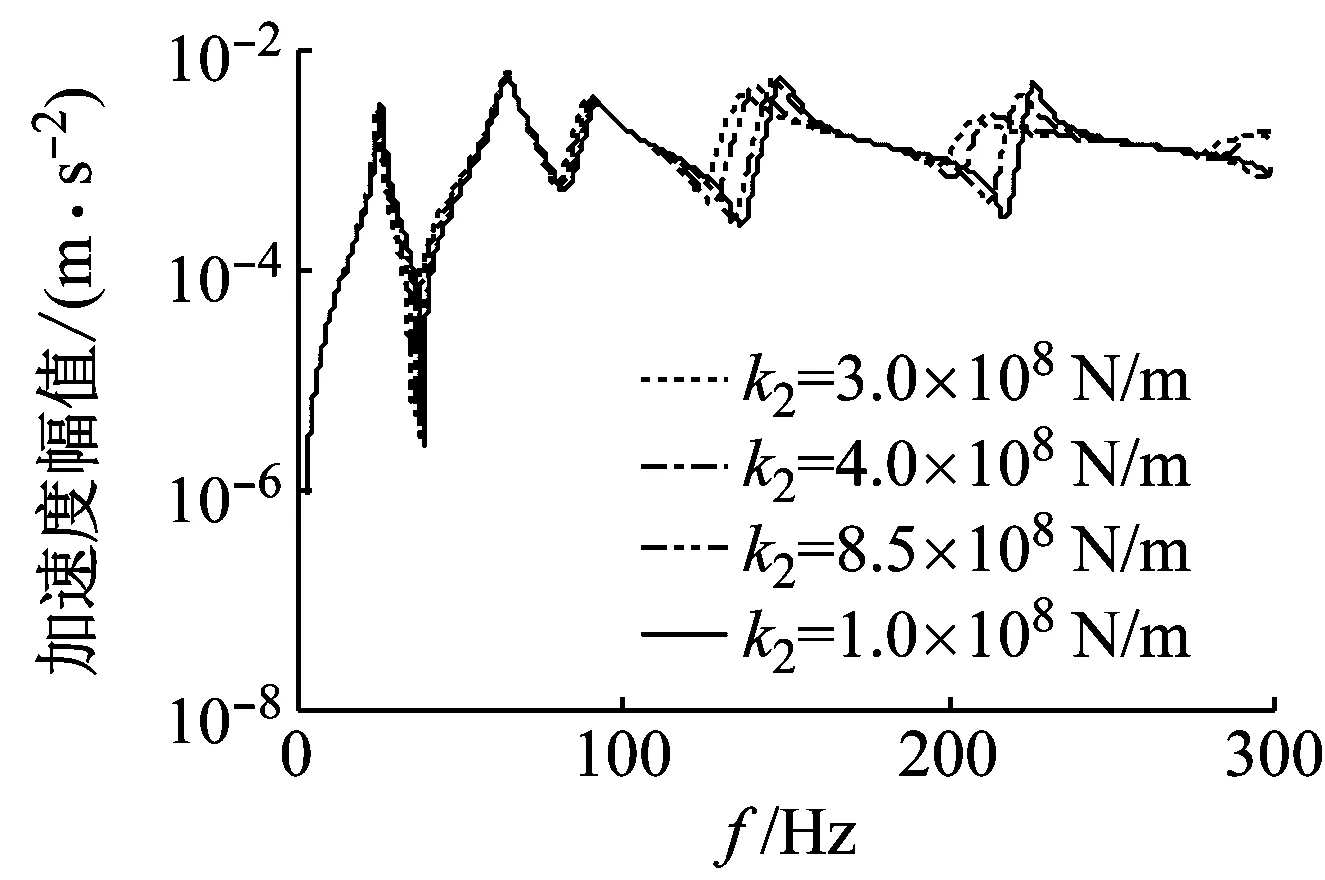
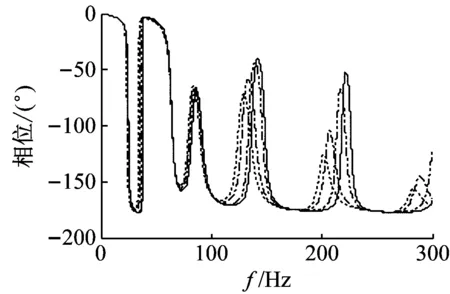
图3 不同参数下控制通道的频响函数Fig.3 FRFs of the control channel at different parameters

2 动态插值自适应控制方法

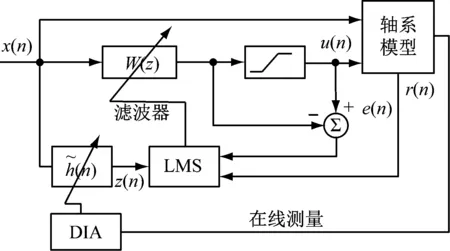
图4 动态插值自适应控制方法框图Fig.4 Block diagram of the dynamic interpolating adaptive control

在控制算法推导过程中，每一个时刻均视为定常系统。在图4中，W(z)是一个N阶FIR自适应滤波器，通过矩阵相乘可以得到u(n)

u(n)=XT(n)w(n)

(18)

式中：X(n)为一个N×M阶矩阵。

X(n)=[x(n)x(n-1) …x(n-M+1)]=

在n时刻，仅在控制力作用下，系统的输出为

(19)

式中：h(n)为n时刻控制通道的脉冲响应序列。

将式(18)代入式(19)可得

y(n)=[XT(n)w(n)]Th(n)=wT(n)X(n)h(n)

在控制之前，利用模态辨识方法得到不同转速下控制通道的脉冲响应序列，再利用Lagrange插值方法对这些数据拟合得到时变的补偿器模型序列。为保证算法的稳定性，不同时刻的补偿器模型与控制通道模型的频域相位误差不能超过90°[15]，相位误差越小，控制效果越好。在控制过程中，DIA根据在线测的转速信号来动态的调整补偿器模型序列。通过合理的选择插值点，使得补偿器模型和控制通道模型等价，即

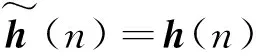
(20)

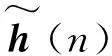
式中：C(n)为一个P×M阶矩阵。

L[r(n)]为插值基函数向量

lk(r)=

式中：rk为选取的插值点。

经补偿器滤波后的参考矢量为

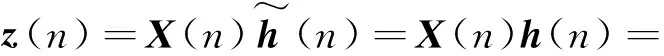
X(n)CT(n)L[r(n)]

则

y(n)=wT(n)z(n)=wT(n)X(n)CT(n)L[r(n)]

式中：z(n)为N×1阶矢量，即

令n时刻干扰作用下产生的干扰信号为d(n)，则误差信号e(n)为

e(n)=d(n)-y(n)

根据误差信号均方值最小准则，代价函数J(n)为

J(n)=E[e2(n)]=E[(d(n)-y(n))2]

将误差信号的均方值替换为瞬时平方值，进行梯度的近似估计

由此得到滤波后LMS算法的权矢量的迭代公式

w(n+1)=w(n)+2μe(n)z(n)

(21)

式中：μ为步长参数，用于迭代步长的调整。

为了加快控制算法的收敛速度，采用归一化LMS算法，并加入饱和抑制单元[16]，考虑这两个因素后的自适应滤波器权矢量的迭代公式

(22)

式中：μ为步长参数或收敛因子，用于自适应迭代步长的调整，0<μ<1，γ>0；Su为Sigmoid函数的一阶导数。

3 纵向振动控制数值仿真

3.1 数值仿真参数

在推进轴系中，推力轴承的纵向刚度会随着转速的增加而减小。为模拟这种动态特性，假设模型中推力轴承的纵向刚度与转速关系式如下

k2=6.50×108+3.55×108cos(0.022r)+

4.18×107sin(0.022r)(N/m)

转速随时间的变化轨迹为

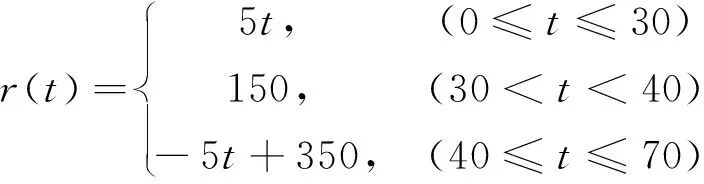
推力轴承纵向刚度和轴速随时间的变化如图5所示，转速先线性增加，再保持不变，最后线性下降。

数值仿真过程中，采样频率为2 048 Hz，自适应滤波器的阶数40，饱和单元的阈值为6 000 N，仿真总时间70 s。 Lagrange插值方法选取的插值点数为7，根据不同插值点对固有频率偏移的影响程度，选择合适的插值点，如图5中所示，星号和圆圈分别表示插值算法中刚度和轴速对应的插值点，其中转速的插值点为1.1 r/min，37.5 r/min，49.4 r/min，70.0 r/min，96.0 r/min，111.4 r/min和150.0 r/min。

图5 纵向刚度和轴速的时间变化历程Fig.5 Trajectory of the longitudinal stiffness and shaft speed

3.2 双频激励下的控制效果

由图3可知，第四和五阶固有频率偏移较大，为验证动态插值自适应方法对这种动态特性时变的系统的控制有效性，采用双频干扰激励，并且两个激励频率142 Hz和216 Hz，分别位于第四和第五阶固有频率变化范围中间。干扰为

x1=250sin(2πf1)+250sin(2πf2)(N)

有、无插值算法的自适应控制仿真结果如图6所示，由图可知，动态插值自适应控制方法能有效的抑制推力轴承的纵向振动，加速度RMS值由12.7g降低到0.2g；在无插值自适应控制下，系统的加速度响应会比无控制下还要大。

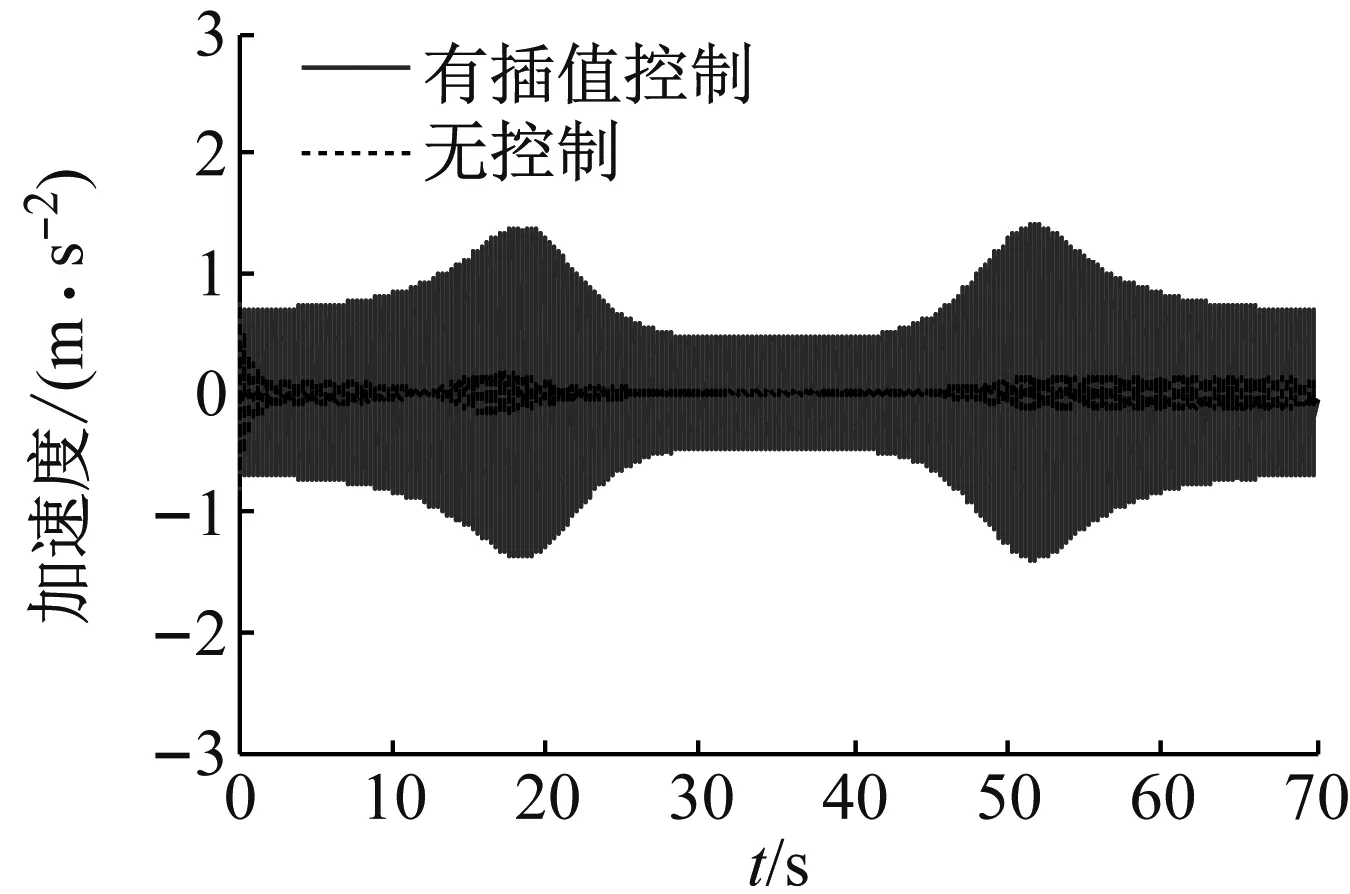
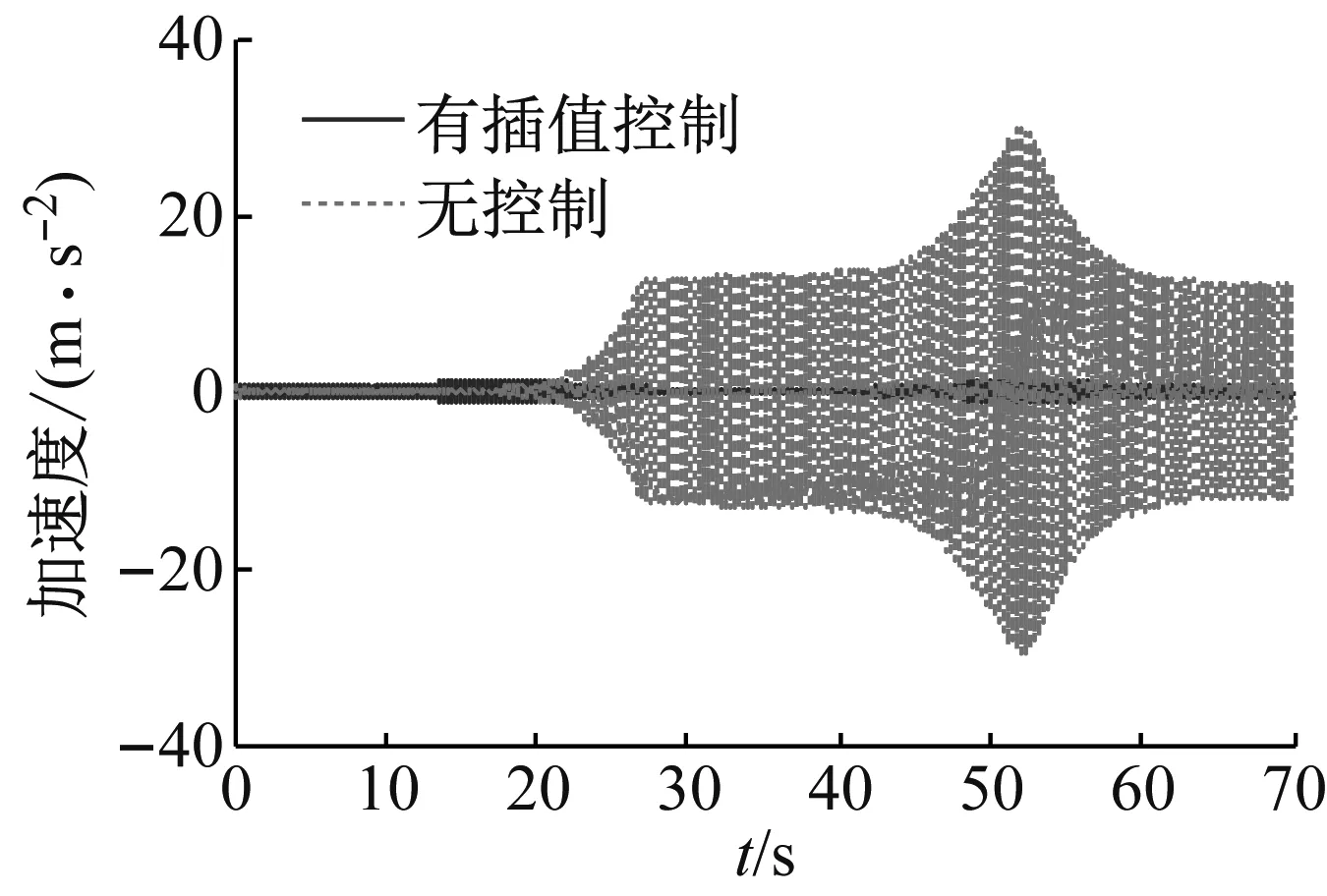
图6 加速度时域响应Fig.6 Acceleration response in time domain

3.3 倍频激励下的控制效果

考虑船舶运行过程中，螺旋桨会受到叶频激励力，激励频率会随转速变化

f=MNr(t)Hz

式中：M=8是螺旋桨的叶片数；N=11是螺旋桨叶频的倍数，假设干扰力大小为

x2=500sin[2πMNr(t)](N)

有、无插值算法的自适应控制仿真结果如图7所示，在插值控制下，振动得到有效控制，推力轴承加速度RMS值由21.7g降低到2.9g；在无插值控制下，在稳态运行状态区间响应变大，其它区间有控制效果。

图7 加速度时域响应Fig.7 Acceleration response in time domain

3.4 控制仿真结果总结与分析

无论在单频还是倍频激励下，动态插值自适应控制方法均能够有效抑制推力轴承的纵向振动，特别是在定转速运行状态下(30～40 s)，33 s时加速度幅值分别降低为无控制下幅值的2.4%和1.26%，算法收敛速度较快。在这两种不同激励下，无插值的自适应控制方法使得系统振动加剧，这是由于选取的定常的补偿器模型和时变的控制通道模型误差较大导致的。在仿真到40 s时，动态插值自适应算法中的时变补偿器模型、自适应算法中的补偿器模型和时变的控制通道模型的频响函数如图8所示，时变补偿器的频响函数几乎和控制通道的频响函数相同，所以控制效果非常好。

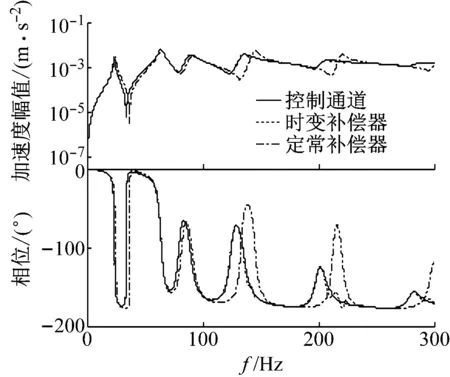
图8 三个不同模型下的频响函数Fig.8 FRFs of three different model

4 结 论

本文建立了推进轴系纵向振动的简化模型，并根据建立的频域矩阵方程求得控制通道和干扰通道的频响函数。针对所建立的纵向振动模型，进行数值仿真。仿真结果表明：在系统动态特性变化较大的情况下，动态插值自适应控制方法能够有效抑制推力轴承的纵向振动，且避免了无插值控制算法导致的系统发散。