整体强制反应位移法适用性分析及修正

陈之毅， 谈忠傲， 楼梦麟

(1．同济大学 土木工程防灾国家重点实验室，上海 200092； 2. 上海市城市建设设计研究总院(集团)有限公司，上海 200125)

随着人们对地下结构地震响应认识的深入，地下结构的抗震问题逐渐引起工程设计及研究人员的重视。起初，地下结构的抗震设计基本上沿用地面结构的抗震设计理念，直到70年代以后，地下结构的抗震设计才逐步形成了独立的体系[1]。目前，土层-结构体系动力时程分析法是复杂结构抗震设计和工程抗震研究的重要手段。其计算结果准确，精度较高，但存在诸如复杂的边界条件处理、地震波筛选、土体非线性动力特性描述等方面的问题而难以全面推广。从最初日本学者大森房吉提出的静力理念到福季耶娃法、“BART”法以及现在常用的反应位移法、反应加速度法，地下结构简化抗震设计方法一直是工程研究人员讨论的重点。近年来，Liu等[2]提出了适用于地下结构的Pushover方法。刘如山等[3]在反应加速度法的基础上提出了有限元反应应力法。但是，这些新兴简化抗震计算方法包括传统的惯性力法等均以施加一定形式的力或者惯性加速度的方式对计算对象进行分析[4]。事实上，正如BART法基本思想所反映出的，地下结构在地震作用下的动力响应受土层变形控制是人们对地下结构震害机制的普遍共识[5]，这与受惯性力控制的地上结构地震反应特征明显不同。因此，现行大多数地下结构抗震计算方法延用地上结构抗震分析施加惯性力的方式让人疑惑。

文献[6]提出一种直接以土层变形作为等效地震荷载的地下结构简化抗震计算方法整体强制反应位移法，着重介绍了该方法的等效荷载分布形式与具体应用步骤，并简单验证了该方法的计算精度。但在实际的工程设计中，结构型式、结构埋深以及场地条件多种多样，因而必须明确简化抗震设计方法的适用范围。本文采用大型通用有限元软件ABAQUS以上海某地铁车站为对象展开数值模拟，分别改变车站结构型式、结构在地基土中的埋深以及地基土的刚度对整体强制反应位移法的适用性进行研究，并采用动力时程分析结果作为比较基准分析了整体强制反应位移法的计算误差及误差产生的原因。

此外，通过前人的研究发现，土层-结构相对刚度是地下结构简化抗震设计中不容忽视的问题。Huo等[7]对1995年阪神地震中发生严重震害的大开车站进行了破坏机理研究，研究发现由于车站不同截面的横截面抗侧刚度不同，土层-结构相对刚度存在差异，结构在相同地震动下产生的侧向变形不尽相同，造成了同一车站的不同截面震害程度不同。所以，土层-结构相对刚度是地下结构抗震设计应当考虑的重要因素。美国在以往的抗震设计中曾认为大多数地下结构的抗剪刚度相对土层抗剪刚度较小，可以直接将结构当成空洞来求解土层变形[8]。该方法的求解结果过于保守，求解的结构内力偏大。整体强制反应位移法使用自由场地震反应分析得出的土层变形作为等效地震荷载估计结构变形实际上是认为结构侧向抗剪刚度与土层剪切刚度相等，存在一定误差。因此，本文定义结构剪切变形修正系数R来考虑土层-结构刚度比F的影响。并通过大量的数值计算拟合得出R-F函数关系，对整体强制反应位移法进行修正，最后通过具体的工况对修正效果进行了验证。

1 整体强制反应位移法

1.1 等效地震荷载

受传统地上结构抗震理念影响，目前大部分地下结构抗震计算方法仍然以惯性力作为等效地震荷载。传统的惯性力法计算地震力的主要思路是将结构上方土柱的水平惯性力简化为作用于顶板的集中力和力矩，结构的地震惯性力作用于结构构件的质心处，在结构一侧作用地震主动土压力，另一侧设置受压弹簧模拟地层的约束作用[9]。由于其过于简化地震产生的荷载，存在较大的计算误差，现已被《城市轨道交通结构抗震设计规范》(GB 50909—2014)等抗震设计规范淘汰。地下结构Pushover法对整个土层-结构计算模型施加单调递增的水平惯性体积力，反应加速度法则将土层地震反应分析时结构顶底板位置发生最大相对位移时的水平惯性体积力施加在土层-结构拟静力模型上[10]，两者在本质上完全相同。而有限元反应应力法将自由土层剪应力分布换算为有限元节点力，其加载方式实际上隐式的等同于惯性力与阻尼力的共同作用。

事实上，不论是早期日本学者对于隧道的地震观测还是Akira、 Hashash等[11]基于原型观测及震动台试验结果均明确指出：地下结构的地震响应主要受周围土层变形控制。这是地下结构抗震问题与地上结构抗震问题的最显著区别。地下结构的抗震计算方法应当紧紧围绕地下结构的地震反应特征，基于土层变形进行抗震计算。目前，主流的抗震计算方法中只有经典的反应位移法将土层变形放在突出位置，并作为结构内力计算的主要影响因素[12]。反应位移法将地震作用下的土层变形通过地基弹簧以静荷载的形式施加在结构上，模型简单、概念清晰[13]。但反应位移法一方面不能准确反应土层对结构的约束作用，另一方面地层弹簧的准确确定费时费力不易掌握[14]。整体强制反应位移法将土层地震反应分析得出的地下结构顶、底板位置达到最大相对位移时沿深度分布的土层水平位移作为抗震分析的等效地震荷载直接施加到土层-结构拟静力模型的土层有限元上。从计算参数上来看，整体强制反应位移法将土层变形作为了结构地震响应的控制因素，相比于反应加速度法等选用土层水平惯性加速度作为施加的外荷载更加符合地下结构的震害机理；在计算模型上，整体强制反应位移法使用土层-结构相互作用模型，能够更好的模拟地震作用下周围土层对结构的约束作用，同时省去了反应位移法等荷载结构法确定地基弹簧系数带来的困难。

1.2 整体强制反应位移法的实施步骤

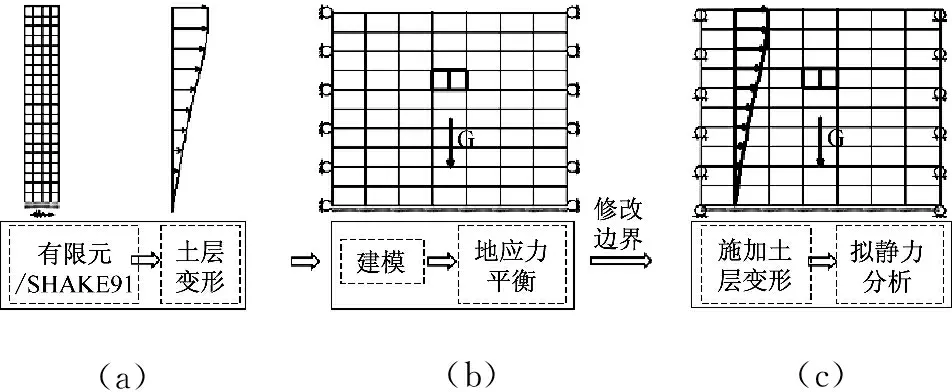
地下结构抗震计算方法整体强制反应位移法的具体实施过程如图1所示。

(1) 求解等效地震荷载。通过等效线性化程序SHAKE91、EERA或者通用有限元分析软件对自由场进行地震反应分析，取土层于地下结构顶、底板位置达到最大相对位移时沿深度分布的土层水平位移作为等效地震荷载。本文采用有限元法。在实际计算中，可选取N条适用于该场地的地震波，分别求得每条地震波计算所得瞬时水平位移分布，取其平均值作为计算的等效地震荷载，以提高计算可靠性。

(a)(b)(c)

图1 整体强制反应位移法实施过程
Fig.1 Step-by-step procedure of integral forced displacement method

(2) 建立拟静力模型并进行地应力平衡。利用有限元软件建立土层-结构相互作用拟静力模型。模型底面边界固定，侧向边界水平向约束，竖向自由。对模型施加重力，并进行地应力平衡。

(3) 重新定义边界条件并进行拟静力计算。撤销模型侧向边界水平向约束代之以地应力平衡之后的水平支座反力，同时约束侧向边界各节点的竖向位移，底面边界仍保持固定；将第一步计算所得的等效地震荷载施加到拟静力模型的土层上，计算结构在地震作用下的响应。

2 分析模型

2.1 基本计算模型与参数

本文计算模型主要以上海某典型两层三跨地铁车站为背景，按照平面应变问题进行考虑。基于大型通用有限元软件ABAQUS建立二维拟静力模型如图2所示。为减小边界效应的影响，结构与侧向边界的距离需为结构宽度的3～5倍，结构底面距模型底边界的距离至少为结构高度的3倍。该模型尺寸长度为200 m，高度为85 m。模型厚度取中柱间距以避免中柱刚度折减问题。模型土层与结构分别采用平面四节点单元(CPE4R)与梁单元(B21)模拟。混凝土本构模型采用线弹性模型。混凝土材料密度为24.5 kN/m3，泊松比为0.2，中柱采用C45混凝土，弹性模量为33.5 GPa，其余部位采用C35混凝土，弹性模量为32.5 GPa；钢筋材料密度为76.4 kN/m3，泊松比为0.3，弹性模量为200 GPa。为了简化问题，土层条件设定为均质土，重度为18.2 kN/m3，弹性模量为49.5 MPa，泊松比为0.29，内摩擦角为31.1°，黏聚力为2 kPa。土体本构模型采用摩尔库伦模型。土与结构之间的接触设置为ABAQUS中自带的面对面摩擦型接触，切向行为采用罚刚度算法，摩擦因数取为0.312，法向行为设定为硬接触。

同时建立二维动力时程模型对整体强制反应位移法的计算结果进行校核。模型长为600 m，高为85 m。结构尺寸、材料参数以及土层参数等设定与拟静力模型相同。底面边界固定竖向位移，为了更好的减弱侧向边界对地震动反射的影响，侧向边界使用无限元(CINPE4)模拟远场。分析步采用ABAQUS隐式动力分析步，时间增量步长的控制采用自动步长技术。为了提高动力计算结果的可靠性，每个工况在计算过程中均采用两条天然波及一条人工波，分别为El-centro波、Imperial_Valley波及《上海市建筑抗震设计规程》(DG J08-9—2013)给出的上海人工波SHW1，时程曲线如图3所示。计算过程中将三条地震波幅值调整一致后沿水平方向输入模型底部边界。

图2 二维拟静力模型(单位：m)Fig.2 Two-dimension pseudo-static model(unit：m)

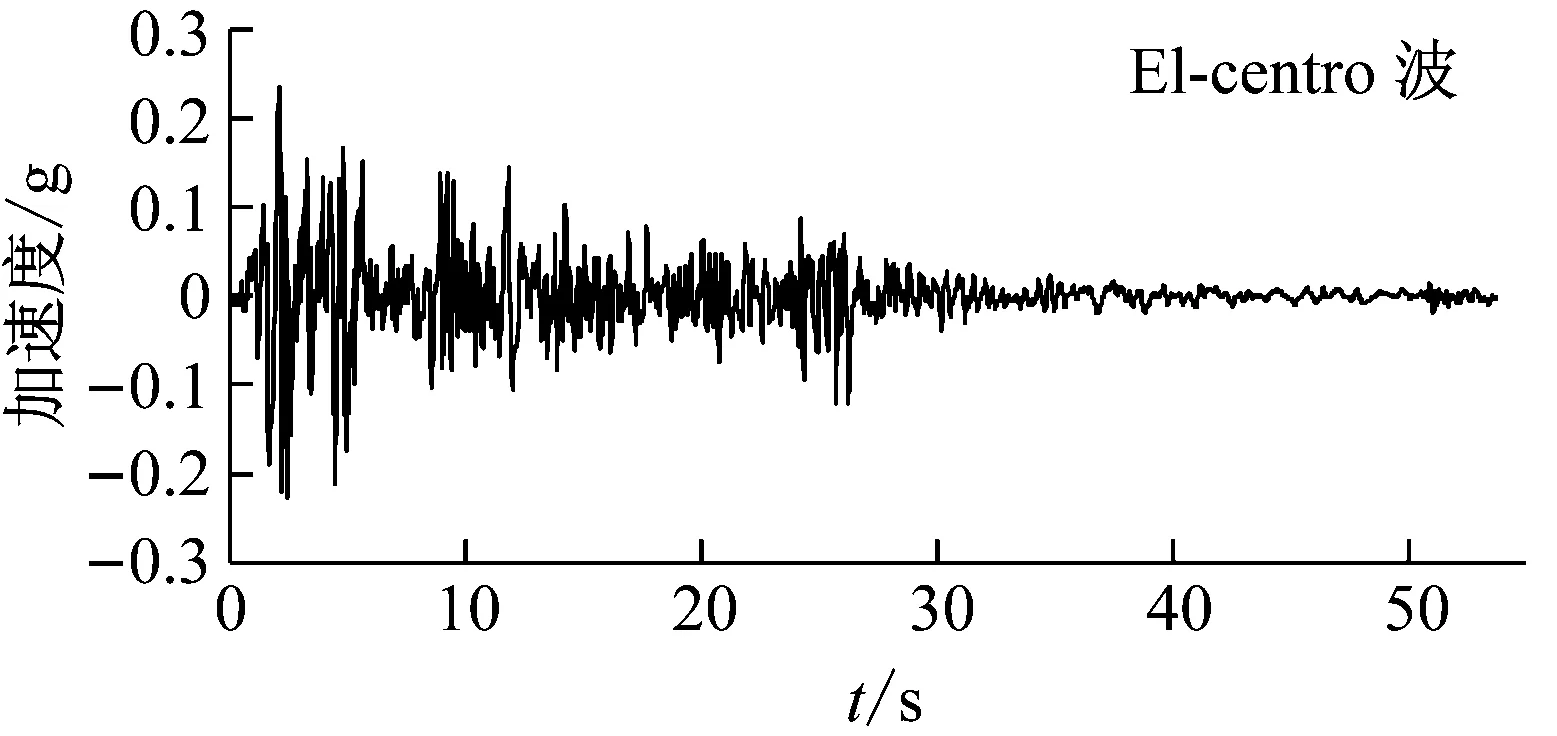
图3 地震波时程曲线Fig.3 Time history of seismic waves

2.2 计算工况

本文针对整体强制反应位移法适应性验证的需求设计了12个工况，分别考察了地下结构抗震计算中可能遇到的3类影响因素。

(1) 结构型式

现代地铁车站的结构型式逐渐向深层次、多功能方向发展。本文选择了三种地铁车站形式，研究整体式强制反应位移法针对不同结构型式的适用性。车站标准断面如图4所示。结构一为单层双跨地铁车站。计算结果分析中主要考虑的控制截面如图4(a)中A～D所示，其中：A,B为中柱顶底端；C为顶板左端；D为侧墙底端。结构二为典型的两层三跨地铁车站，所考虑的控制截面同样如图4(b)上A～D所示，其中：C表示中间楼板左端；其余位置与结构一相同。结构三为四层三跨地铁车站，由于结构三层数较多，故本文考虑了较多的控制截面，图4(c)中：A，B为底层中柱顶底端；C～E为相应位置中柱底端；F为顶板最右端;G为所标楼板最右端;H为侧墙底端。

(a) 结构一(b) 结构二

(c) 结构三图4 车站结构标准断面(单位：m)Fig.4 Cross section of the subway station(unit：m)

(2) 结构埋深

现代地铁车站大部分顶板埋深在6 m以内。但是随着施工技术的进步和地下空间的利用，地铁车站向着大深度、大规模方向发展是必然趋势。为此在其他条件不变的情况下，分别将结构顶板埋深设定为3 m，6 m，9 m，15 m，20 m，25 m进行分析，研究整体强制反应位移法对于不同结构埋深的适用性。

(3) 场地条件

由于土层-结构模型中的地下结构取代了原来自由场中的一部分土体，使得由自由场得出的等效地震荷载与实际作用在结构上的地震荷载存在一定差别，且随着刚度比的变化，该差异更加显著[15]。根据土层剪切波速与弹性模量之间的关系，本文通过改变原型土层的剪切波速，改变土层弹性模量进而实现地基土体刚度的变化。原型土层属于四类土为柔软土层，剪切波速为102 m/s。将土层剪切波速设定为204 m/s和306 m/s，重新设定后的土层能够大致代表三类土与二类土，以此研究整体强制反应位移法在中软土及中硬土中的计算效果。

2.3 适用性分析

2.3.1 对比基准状态的确定

为了合理的比较整体强制反应位移法与动力时程法的计算结果，将两个分析过程中结构顶底板达到最大相对位移时的状态定为对比基准状态。其中，整体强制反应位移法的对比基准状态即为计算的最终状态，动力时程法对比的基准状态一般为某个中间状态。在动力分析过程中每一个工况均需读取三条地震波各自基准状态的计算结果，并求其平均值作为最终结果对整体强制反应位移法的计算结果进行校核。

2.3.2 结构型式的影响

分别计算结构一、结构二、结构三在土层剪切波速为102 m/s，地震动强度为0.1g，结构顶板埋深为3 m情况下的动力响应以研究整体强制反应位移法对不同结构型式地下结构抗震计算的适用性。图5给出了不同结构型式下整体强制反应位移法计算所得内力结果与动力时程法计算结果的对比。Md，Qd表示动力分析法计算得到的弯矩和剪力，Ms，Qs表示整体强制反应位移法计算得到的弯矩和剪力。其中边墙及板的内力均为每米结构的总内力，中柱则为单根中柱的内力。图5～图7中的符号具有相同含义，后文不再赘述。由图可以知，整体强制反应位移法在不同结构型式的地铁车站下的计算误差略有增大。就弯矩而言，单层双跨的结构一总体计算误差在5%左右；而两层三跨的结构二与四层三跨的结构三大部分控制截面误差在10%左右，仅仅在结构三控制截面E与控制截面F两处误差较大，分别为30%和38%。就剪力而言，结构一计算误差同样较小；结构二最小误差为8%，最大误差为20%；结构三最小误差为5%，E，F两处的计算误差较大分别为29%，22%。

分析可知，一方面，根据Wang的土层结构剪切刚度比F定义，从结构一到结构三，结构体型的变化造成了结构抗剪刚度增大，土层结构剪切刚度比减小进一步使得等效地震荷载的精确度降低，导致误差增大；另一方面夏晨等[16]指出对于刚度越大的地下车站结构，周围土体对结构的约束作用越弱，结构惯性力等因素的对其动力响应的影响增大，也导致整体强制反应位移法的计算误差增大。总之，结构体型越小(如：结构一)自由场计算得出的等效地震荷载与结构受到的真实地震作用越接近，整体强制反应位移法计算误差则越小；反之，计算误差增大。但是，结构型式变化产生的影响与上节所分析土层刚度的影响相比很小，所以整体强制反应位移法对于不同结构型式具有较好的适用性。

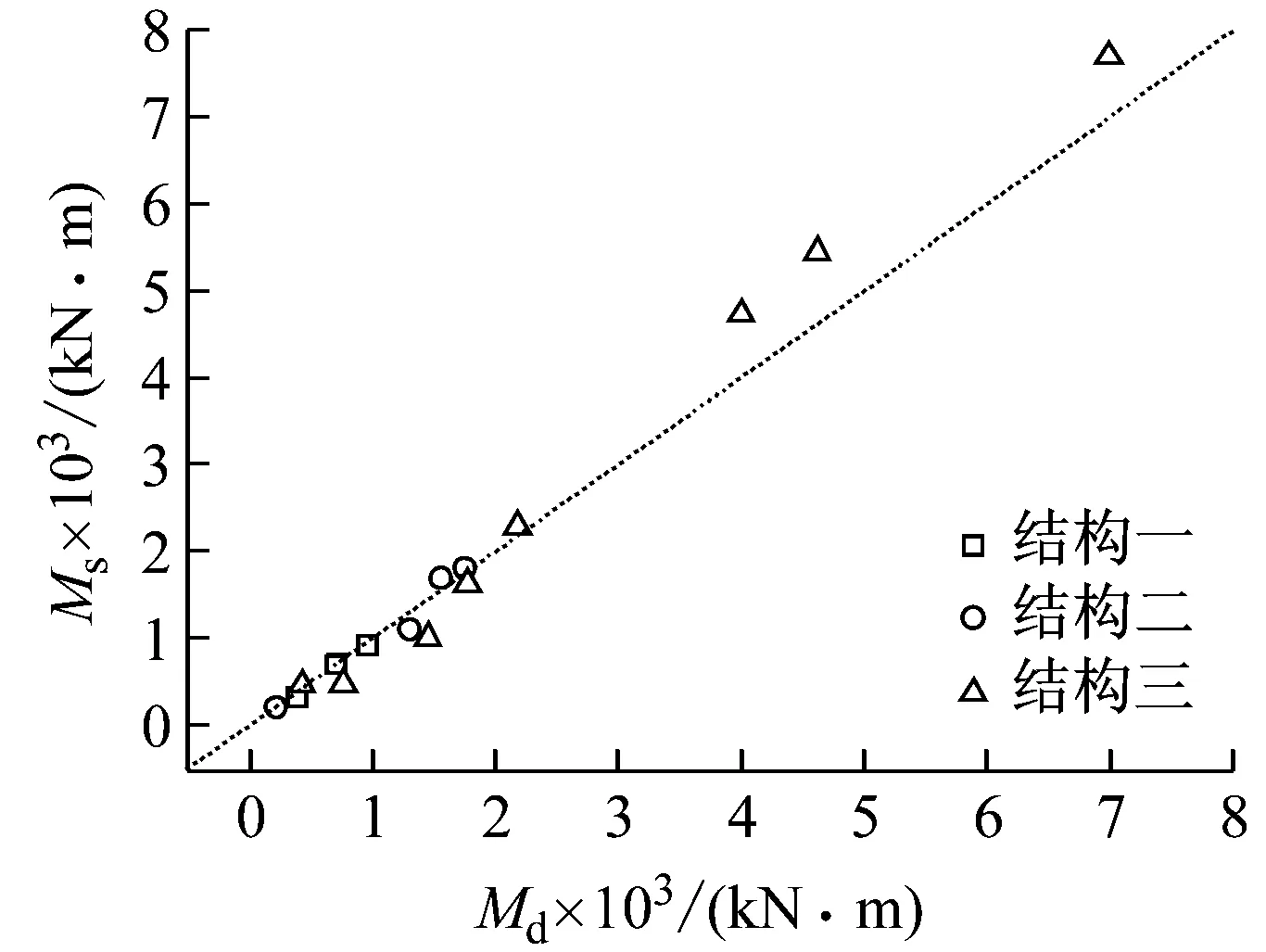
(a) 弯矩对比

(b) 剪力对比图5 不同结构型式的计算结果对比Fig.5 Comparison of internal forces

2.3.3 地下结构埋深的影响

选取结构二，设定土层剪切波速为102 m/s，地震动强度为0.1g，分别改变结构顶板埋深以研究整体强制反应位移法对不同埋深地下结构抗震计算的适用性。图6给出了整体强制反应位移法及动力时程法计算结果的对比情况。在针对不同车站埋深的适用性研究中，整体强制反应位移法与动力时程法计算所得内力结果符合良好。大部分控制截面的弯矩误差在10%左右，且随着埋深的增加，误差有减小的趋势。所有埋深工况下的最大弯矩计算误差出现在车站顶板埋深为6 m时，控制截面A误差达21%。各个埋深工况下，中柱控制截面的剪力计算误差大部分在10%左右，而边墙与楼板控制截面剪力误差相对较大，一般在20%左右。当结构埋深增加到20 m以上时，整体强制反应位移法计算所得弯矩与剪力误差均仅在5%左右。

从图6可知，在各埋深工况的计算中，整体强制反应位移法的计算结果较动力时程法的计算结果偏大。这是因为在算例中，地基土刚度比地下结构的刚度小，所以无结构的自由场计算得出的等效地震荷载偏大，故整体强制反应位移法的计算结果也偏大。另一方面，当结构埋深大时，结构受到土体约束较大，随着埋深减小，土层约束减弱，结构自身地震特性影响增大。由于整体强制反应位移法忽略了在地震作用下，结构自身惯性力的影响，所以在结构埋深较小时计算误差相对较大。从总体来看，整体强制反应位移法适用于不同埋深的地下结构抗震计算。

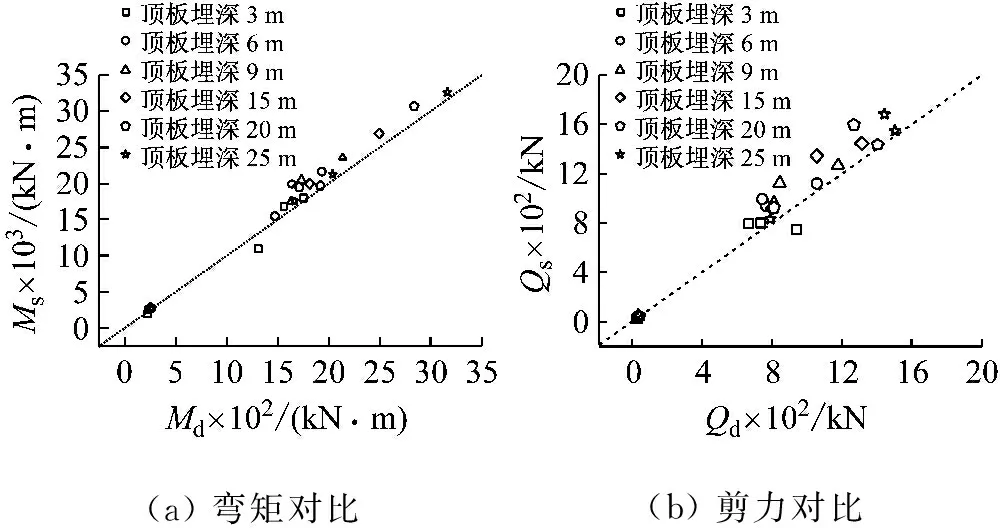
图6 不同埋深下的计算结果对比Fig.6 Comparison of internal forces under differen cases of soil cover

2.3.4 土层刚度的影响

选定结构二，顶板埋深3 m，地震动强度为0.1g，设定地基土剪切波速分别为102 m/s,204 m/s，306 m/s以研究整体强制反应位移法对不同土层刚度下地下结构抗震计算的适用性。图7表示不同土层刚度条件下整体强制反应位移法计算所得内力结果与动力时程法计算结果的对比。随着土层刚度的增大，整体强制反应位移法的计算误差呈增大趋势。土层剪切波速为初始剪切波速即Vs=102 m/s时，弯矩最小误差仅有5%，最大计算误差为15%；而Vs=204 m/s时，弯矩最小误差为8%，最大误差增加到34%；Vs=306 m/s时，弯矩计算误差总体在35%左右。剪力计算误差的变化趋势相同，但是误差相对弯矩误差稍小，土层剪切波速Vs=306 m/s时，最小和最大剪力计算误差分别为26%和42%。

图7 不同土层刚度下的计算结果对比Fig.7 Comparison of internal forces under different cases of soil stiffness

由图可以看出土层刚度增大后整体强制反应位移法的计算结果普遍小于动力时程的计算结果。这是因为随着土层刚度的增大，通过自由场地震反应分析得出的土层水平位移小于结构在地震作用下产生的真实剪切变形，以前者作为等效地震荷载对结构变形及内力的估计偏小。并且这种差异随土层刚度的增大逐渐增大，导致整体强制反应位移法的计算误差也越来越大。可见，目前整体强制反应位移法对于软土地下结构抗震计算具有较好的适用性，而在中软土或中硬土中适用性较差。

3 考虑土结刚度比的修正

3.1 结构剪切变形修正系数R、土结刚度比F及其关系

整体强制反应位移法通过求解自由场地震反应分析得到的等效地震荷载来估计结构在地震作用下所受真实荷载水平。显然，自由场地震反应分析忽略了实际情况下的土层-结构相互作用问题。因此前文整体强制反应位移法适用性分析中土层刚度工况下的计算结果不理想。简单采用自由场地震反应分析得出的土层位移分布并不能完全反应结构在动力作用下的变形情况。因此本文作如下定义

(1)

式中：δ1为通过动力时程法计算得到结构顶底板的最大层间位移角，即结构侧向剪切变形；δ2为通过自由场地震反应分析计算得出的结构所在位置的土层总体剪应变。两者计算方式相同，均为侧向水平相对位移除以结构高度。

土结刚度比法F采用Wang的定义

(2)

式中：G为土层剪切模量；H为结构的高度；L为结构长度；S1为结构顶底板产生单位相对位移所需要的力。

本节围绕土结刚度比F，同时综合考虑结构型式、结构埋深、地震动频谱特性等因素的影响设计了36组算例。结构型式依然选用了第2.2节介绍的单层两跨、两层三跨、四层三跨三种较常用的地铁车站横截面型式。由于现有地铁车站一般顶板埋深较浅在3 m左右，设定结构顶板埋深为1 m，3 m，6 m，9 m四种情况足以反应实际工程中结构埋深不同带来的影响。输入地震动选择了低频为主的El-centro波和高频为主的Chichi波以考虑地震谱频谱特性不同的影响。参考场地条件一类土～四类土的土层剪切波速变化范围，在土层剪切波速为60 m/s的软弱土到400 m/s的中硬土之间设计了12组土层剪切波速来反应模型中土层抗剪刚度的变化。由此，造成的土层-结构剪切刚度比F的变化范围大约在0.4～19，能够反应软弱土层中结构抗剪刚度大于土层抗剪刚度即F<1的情况也能反应多数情况下的土层抗剪刚度较结构抗剪刚度大即F>1的情况。限于篇幅，具体的计算工况表不再赘述。

从理论上分析，当结构抗剪刚度等于土层抗剪刚度即F=1时，自由场在地震作用下的侧向变形应当等于土层-结构体系在地震作用下的侧向变形，所以R=1。为了控制数值模拟结果反应该特点，根据计算结果的数据分布形式对横坐标土结刚度比F取对数ln(F)，对R-ln(F)图做线性拟合，并控制截距为1，表示当土结相对刚度F=1时，结构剪切变形修正系数R=1。线性拟合所得R-ln(f)曲线如图8所示，其函数关系如下

R=0.276ln(F)+1

(3)

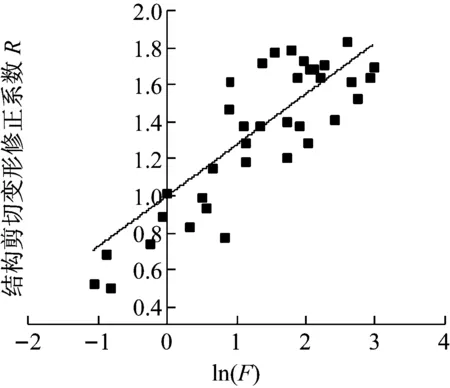
图8 R-ln(F)计算结果及线性拟合Fig.8 R-ln(F) calculation results and linear fitting

修正的整体强制反应位移法即根据式(2)计算得出土层-结构刚度比Fi代入式(3)计算结构剪切变形修正系数Ri，再将自由场地震反应分析得出的最不利土层水平位移乘以结构剪切变形修正系数展开整体强制反应位移法以考虑土结刚度比导致的自由场土层变形与地震作用下结构真实变形的差异。使得整体强制反应位移法的计算结果更准确的反应地下结构的在地震作用下的动力响应。

3.2 修正效果验算

本文第2.3.4节中随着土层刚度的增大，整体强制反应位移法的计算误差逐渐增大，从10%逐步上升到40%左右。而在不同结构型式适用性验证中，整体强制反应位移法计算误差较稳定是因为结构型式的变化引起的土结刚度比变化相对较小。结构一～结构三在土层剪切波速为102 m/s的场地中的土结刚度比F分别为1.15，1.21，0.96。因此，本节对不同土层刚度下的三种工况采用修正的整体强制反应位移法进行计算，以验证R-F曲线及其拟合公式对于整体强制反应位移法的修正效果。

3.2.1 等效地震荷载调整

整体强制反应位移法的修正实际上正是等效地震荷载的修正。三种工况下，修正前和修正后的等效地震荷载如图9所示。

(a) Vs=100 m/s

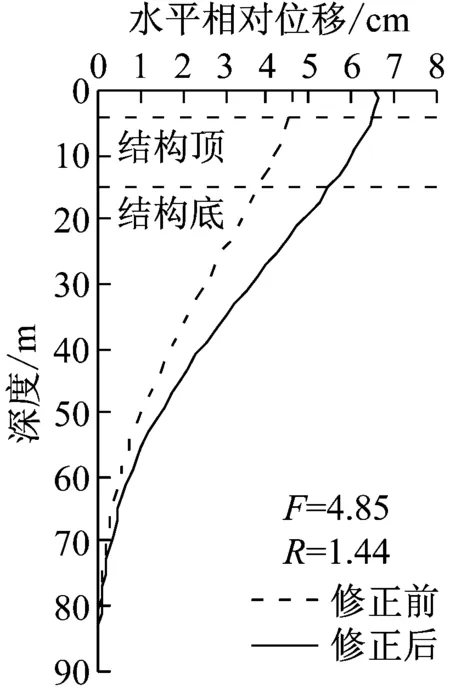
(b) Vs=200 m/s

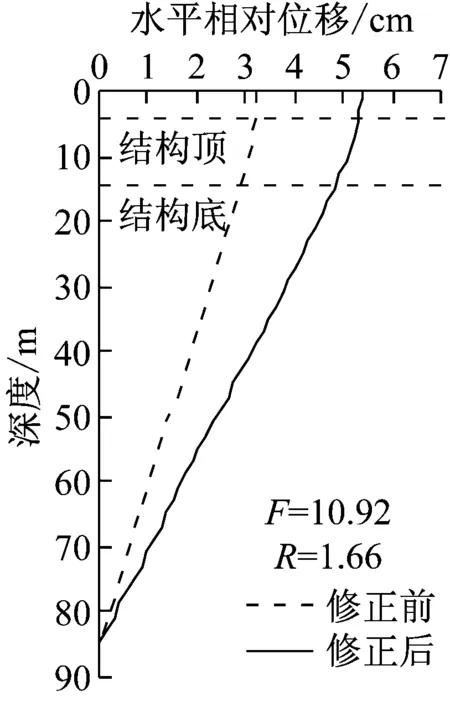
(c) Vs=300 m/s图9 各工况等效地震荷载修正Fig.9 Original and modified equivalent seismic load

3.3.2 计算结果对比

整体强制反应位移法修正前与修正后的计算结果如图10所示(注：填充符号表示修正前的内力数据，空心符号表示修正后的内力数据)。由图10可知不论对于弯矩还是剪力，修正后的整体强制反应位移法的内力计算结果更接近动力时程分析结果，总体上使得原本的整体强制反应位移法计算结果往误差更小、更偏安全的方向发展。Vs=204 m/s和Vs=306 m/s两种土层刚度情况下的计算准确性尤为明显，修正前的计算误差随着土层刚度的增大而增大到30%以上。而修正后绝大部分控制截面计算误差明显改善，误差减少一半以上，普遍在10%～20%甚至小于5%。这说明ABAQUS数值模拟得出R-F曲线及拟合公式具有明显的修正效果，满足简化抗震设计需求，使得原本难以考虑土层-结构相对刚度的基于土层变形的地下结构简化抗震设计方法整体强制反应位移法得以改进，适用性及计算精度进一步改善。

(a) 弯矩对比

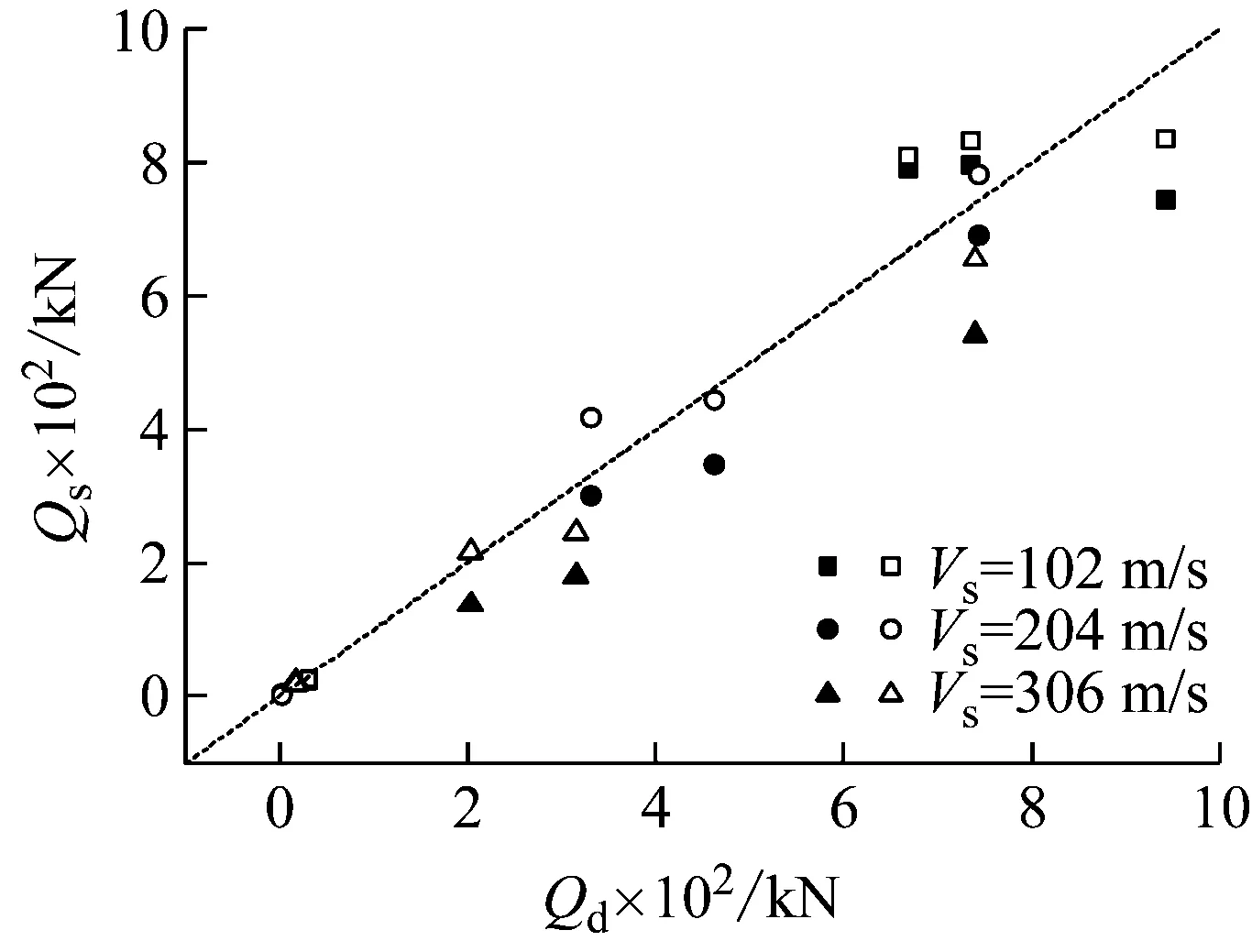
(b) 剪力对比图10 修正前后内力计算结果对比Fig.10 Comparison of internal force calculation results before and after modification

4 结 论

本文通过改变地下结构在地基土中的埋深、输入地震动强度、地基土刚度与地铁车站结构型式，对整体强制反应位移法进行了适用性验证。对于整体强制反应位移法不能考虑的土结刚度比问题提出采用结构剪切变形修正系数R进行修正。得出以下结论：

(1) 整体强制反应位移法对于不同车站结构型式均具有较强的适用性。地铁车站结构体型增大，整体强制反应位移法计算误差略有增加，但总体上仍与动力时程分析法的计算结果符合良好。

(2) 整体强制反应位移法能够很好的适用于各个埋深下的地下结构抗震计算，并且随着埋深的增加计算误差明显减小。对于深埋地下结构，计算误差仅为5%。同时发现地震引起的结构内力亦随着埋深的增大而减小，与深埋结构震害较轻的认识相吻合。

(3) 整体强制反应位移法能够很好的适用于软土地下结构抗震计算，但是在中硬土中适用性欠佳。在软弱地基中，整体强制反应位移法的计算精度良好，误差基本在10%以内；在中硬地基中误差有所增大，大多数控制截面误差达到30%。

(4) 原先的整体强制反应位移法难以考虑实际工程中的土结刚度比问题。通过数值模型结果拟合得出的结构剪切变形修正系数R与土结刚度比F的函数关系对整体强制反应位移法具有良好的修正效果。修正后的整体强制反应位移法在各土层刚度工况下的计算结果与动力时程结果相比，误差基本在10%左右。

总之，整体强制反应位移以土层变形作为等效荷载形式更加符合地下结构的地震响应特征，打破了以往参照地上结构抗震分析施加惯性力的传统方式。方法概念清晰、易于实现，于此同时也具有良好的计算精度，可供工程设计参考应用。