不同重力环境下含间隙旋转铰位置特性仿真研究

刘福才， 兰 会， 刘 林， 赵 旭

(燕山大学 工业计算机控制工程河北省重点实验室， 河北 秦皇岛 066004)

随着航天工程领域的发展，人类对系统动力学行为的精确预测要求愈渐迫切。在机械系统中，运动副是连接两构件，并使之发生相互接触及相对运动的中间环节。而运动副的设计过程中的余量、制造过程的误差以及机械系统长时间运转过程中的磨损等，均会导致一定的运动副间隙。因此，机构中运动副存在间隙是不可避免的。运动副间隙大大影响机构的动特性，使机构的实际运动和理想运动之间产生了偏差[1]。这就使得在进行精密机构的分析和设计时，不得不对运动副间隙加以考虑。因此，对于含间隙机构的建模方法、对机构运动学和动力学以及含间隙机构的运动规律的研究是必要的。

目前常用的机械系统含间隙旋转铰近似等效模型有三种：连续接触模型、接触-分离二状态模型和接触-分离-碰撞三状态模型。连续接触模型由Earles等[2]首次提出。Seneviratne等[3]利用连续接触模型分析了曲柄摇杆机构中间隙运动副元素的混沌运动。王璐[4]采用连续接触模型，建立了铰链式运动副间隙的有效杆长输出运动误差模型。并以四杆机构为例，运用矩阵法分析了间隙对机构输出误差的影响。王庚祥等[5]基于连续接触模型研究空间球面副间隙对并联机构动力学性能影响，分析了关节间隙对该并联机构运动学特性及驱动力影响。王华杰等[6]利用连续接触等效模型，进行了含间隙曲柄摇杆机构的动力学仿真研究。Dubowsky等[7-11]陆续提出了一维冲击副、一维冲击杆、二维冲击环等模型，并利用这些模型对含间隙机构动力学进行定量分析。王国庆等[12]分析了间隙铰接触的特点，采用非线性弹簧阻尼模型描述碰撞分离过程，建立了含间隙曲柄摇杆机构的动力学模型。黄玮等[13]以曲柄滑块机构为例，应用非连续接触模型和连续接触模型，分析运动副径向间隙和轴销位置的不确定性因素对机构运动可靠性的影响。刘福才等[14]根据弹簧阻尼模型建立了地面装调及空间服役两种不同工况下的近似间隙等效模型，并设计了间隙补偿器。李海阳等[15-16]采用二状态间隙等效模型，在机动武器系统的含摩擦碰撞模型基础上建立了旋转间隙铰模型，并进行了动力学仿真研究。Mansour等[17]研究了高速含间隙机构的冲击力和冲击力矩。白争锋等[18]建立了一种改进的间隙非线性连续接触碰撞力的混合模型，同时采用修正的库仑摩擦模型描述间隙处的摩擦作用，并且建立的间隙接触碰撞力的混合模型拓展了间隙铰接触碰撞动力学建模与含间隙机构动力学特性的研究。刘福才等[19]设计了基于模糊控制原理的改进型自抗扰控制器，实现了对挠性航天器的振动的快速有效抑制。

上述关于运动副间隙对机构动态特性的影响主要是在重力场中进行的，而对于不同重力环境对含间隙旋转铰运动行为的研究考虑的较少。空间机构主要是在太空微重力场下环境中工作，但是研究设计工作主要是在地面进行，地面模型实验及实物实验都将受到重力的影响。对于空间机构，在地面模拟三维微重力场的实验是比较困难的，因此数值仿真研究更为重要。本文将对此进行数值仿真，研究重力场对含间隙旋转铰运动行为的影响。

本文为研究不同重力环境下间隙对连杆机构运动行为的影响，采用连续接触模型，将运动副间隙等效为无质量轻杆，使含间隙的曲柄摇杆机构增加一个自由度，等效为一个无间隙五连杆机构，并在ADAMS软件中建立连杆机构模型，设置不同的重力环境、不同间隙、不同转速等多种情况，对连杆运动情况进行模拟仿真研究。

1 含间隙旋转铰模型的建立

通过对含间隙机械系统的分析，不难知道，机构运动过程中，含间隙旋转铰的轴销与轴套之间的相对运动状态分为三种：分离、接触和碰撞。但是实际建模过程中，将含间隙旋转铰的这三种相对运动状态都考虑其中是十分困难的，而且在机构实际运动过程中，尤其是当机构高速运转时，轴销与轴套发生分离和碰撞的过程时间极短，在一个运动周期中，绝大部分时间轴销与轴套都处于接触状态。连续接触模型的主要思想就是忽略含间隙旋转铰轴销与轴套之间的碰撞和变形，认为轴销和轴套始终处于接触状态，将间隙等效为一根无质量的轻杆。连续接触等效模型增加了机构的自由度，但整个机构仍处于完整的约束状态，其等效模型如图1所示。

本文以含间隙曲柄摇杆机构为例研究不同重力环境下含间隙旋转铰位置特性，假设在机构的连杆和摇杆机构连接处的运动副存在间隙，根据连续接触模型，将运动副间隙用一个无质量轻杆代替，从而使得含间隙的曲柄摇杆机构近似等效为无间隙的五连杆机构，含间隙曲柄摇杆机构模型图如图2所示。图中的间隙是经过放大的示意图，图中的杆1,2,3,4分别表示曲柄、连杆、摇杆和机架，L1，L2，L3，L4分别为各杆件长度，R1，R2和R3依次为曲柄、连杆和摇杆的质心，d和ρ则为半径间隙大小(即间隙轻杆的长度)和间隙杆的方向。假设初始时刻运动副轴销与轴套处于接触状态，分析模型易知，当间隙轻杆受力为零或者受压时，则轴销与轴套将脱离接触状态。

图1 含间隙旋转铰连续接触等效模型Fig.1 Equivalent model of continuous contact with clearance

图2 含间隙曲柄摇杆机构模型示意图Fig.2 Schematic diagram of the crank-rocker mechanismwith clearance

图2所示的含间隙曲柄摇杆机构自由度为2，取φi和ρ为独立广义坐标。设曲柄匀速转动，则由几何关系可得机构封闭环方程

L1ejφ1+L2ejφ2+dejρ+L3ejφ3+L4ejφ4=0

(1)

本文基于间隙的连续接触等效模型，不考虑运动副中摩擦力的影响，则在重力环境下，连杆和摇杆关于B点和D点的力矩平衡方程如下

(2)

(3)

求解两方程，得到系统动力学微分方程

(4)

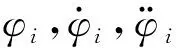
当机构处于微重力环境时，径向间隙所在平面基本不受重力影响，则系统动力学微分方程如下

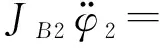
(5)

2 基于ADAMS的含间隙曲柄摇杆机构仿真研究

平面四杆机构是最简单的平面连杆机构，它是组成多杆机构的基础。而前人的研究中，针对平面四杆机构的研究也是相当多的。本文综合考虑仿真完成难度、仿真结果有效性和仿真耗时，决定优先选用最简单的连续接触模型进行建模，将运动副的径向间隙假想成无质量间隙杆，将曲柄摇杆机构转化为五杆机构，设间隙大小为1 mm，曲柄摇杆机构尺寸如表1所示。

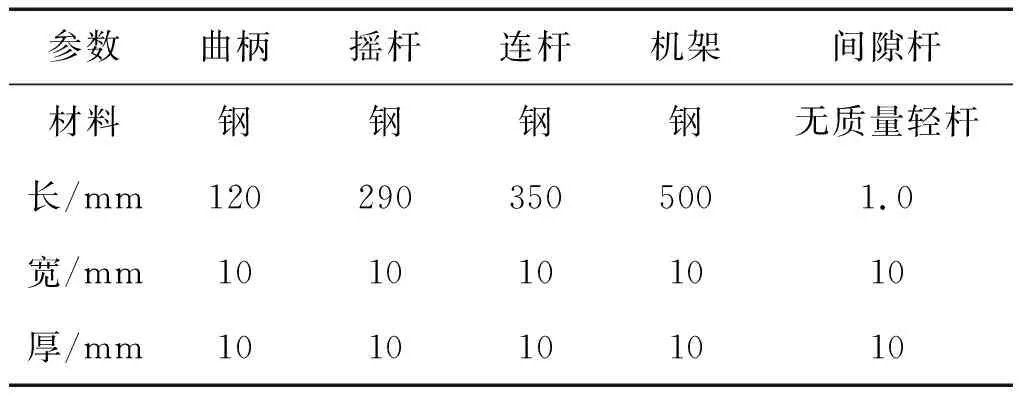
表1 含间隙曲柄摇杆机构模型设计参数Tab.1 Parameters for crank-rocker mechanism with clearance

图3为ADAMS软件中搭建的含间隙曲柄摇杆机构模型，假设在曲柄摇杆机构的连杆和摇杆之间的运动副处存在间隙，并分别用0.2 mm，0.5 mm和1.0 mm的无质量轻杆代替，使含间隙曲柄摇杆机构增加一个自由度，将其等效为无间隙五连杆机构。曲柄以设定的转速匀速转动，且不考虑摩擦力。

在ADAMS软件中完成含间隙曲柄摇杆机构的不同重力环境、不同间隙大小以及不同曲柄转速下的仿真实验。选取1g和0两种情况，0.2 mm，0.5 mm，1.0 mm等三种间隙，6.25 r/min,50 r/min,115 r/min等多种速度进行仿真，记录间隙杆的起始点和末端点的坐标位置数据，并将数据导出，在Matlab中绘制含间隙曲柄摇杆机构运动过程中间隙杆末端点相对于起始点的X轴位移、Y轴位移、质心运动轨迹以及间隙杆与X轴正方向的夹角(相位角ρ)的变化。

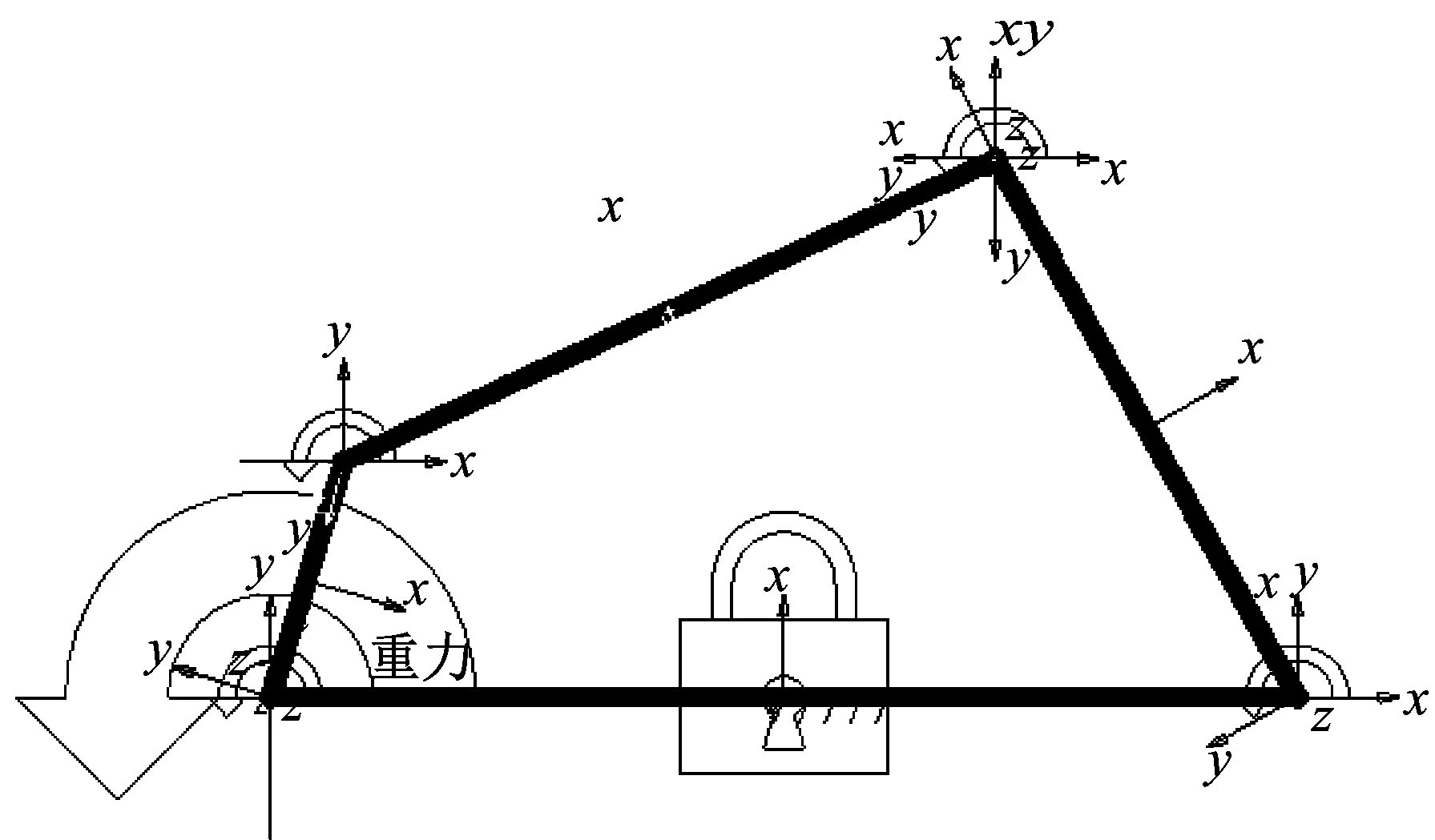
图3 含间隙曲柄摇杆机构模型Fig.3 The model of crank-rocker mechanism with clearance

2.1 重力场加速度为1g时的仿真结果

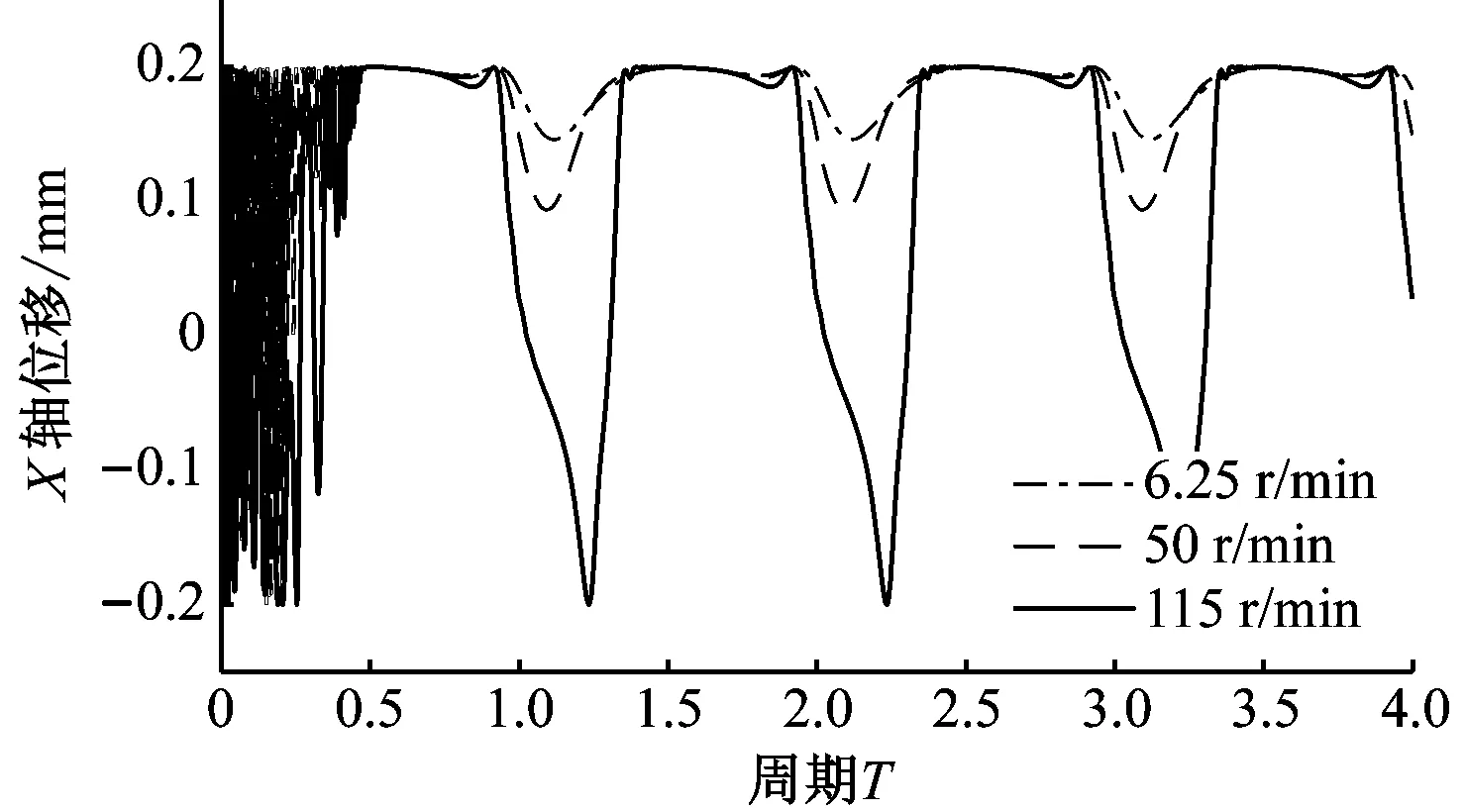
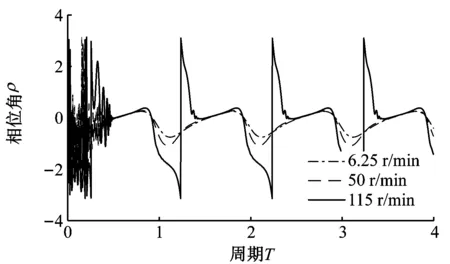
重力场加速度为1g，间隙为0.2 mm时的仿真结果如图4所示。由于仿真实验只考虑了重力，没有考虑摩擦力以及机构实际运动过程中的各种干扰，仿真过程基本属于理想状态，由图4的X轴、Y轴位移以及相位角变化图可以看出，只有在仿真初始时刻会有比较大的抖动，这是由于模型初始位置选取在了不符合力的平衡的位置，致使仿真开始时间隙杆发生摆动引起的。间隙轨迹图中的圆代表含间隙运动副中的轴颈与轴套处于持续接触的状态下轴颈中心的轨迹，起到参照的作用。

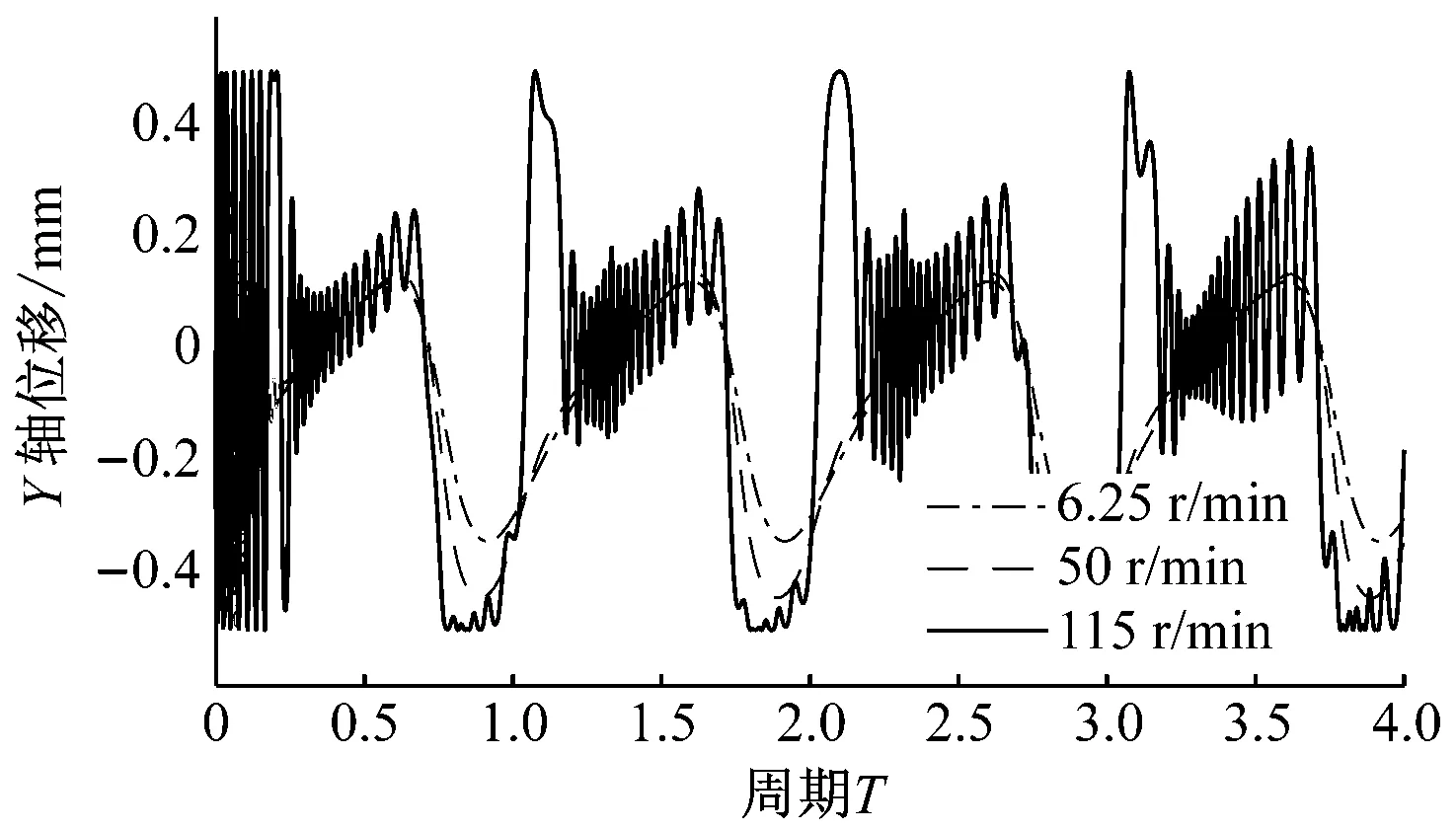
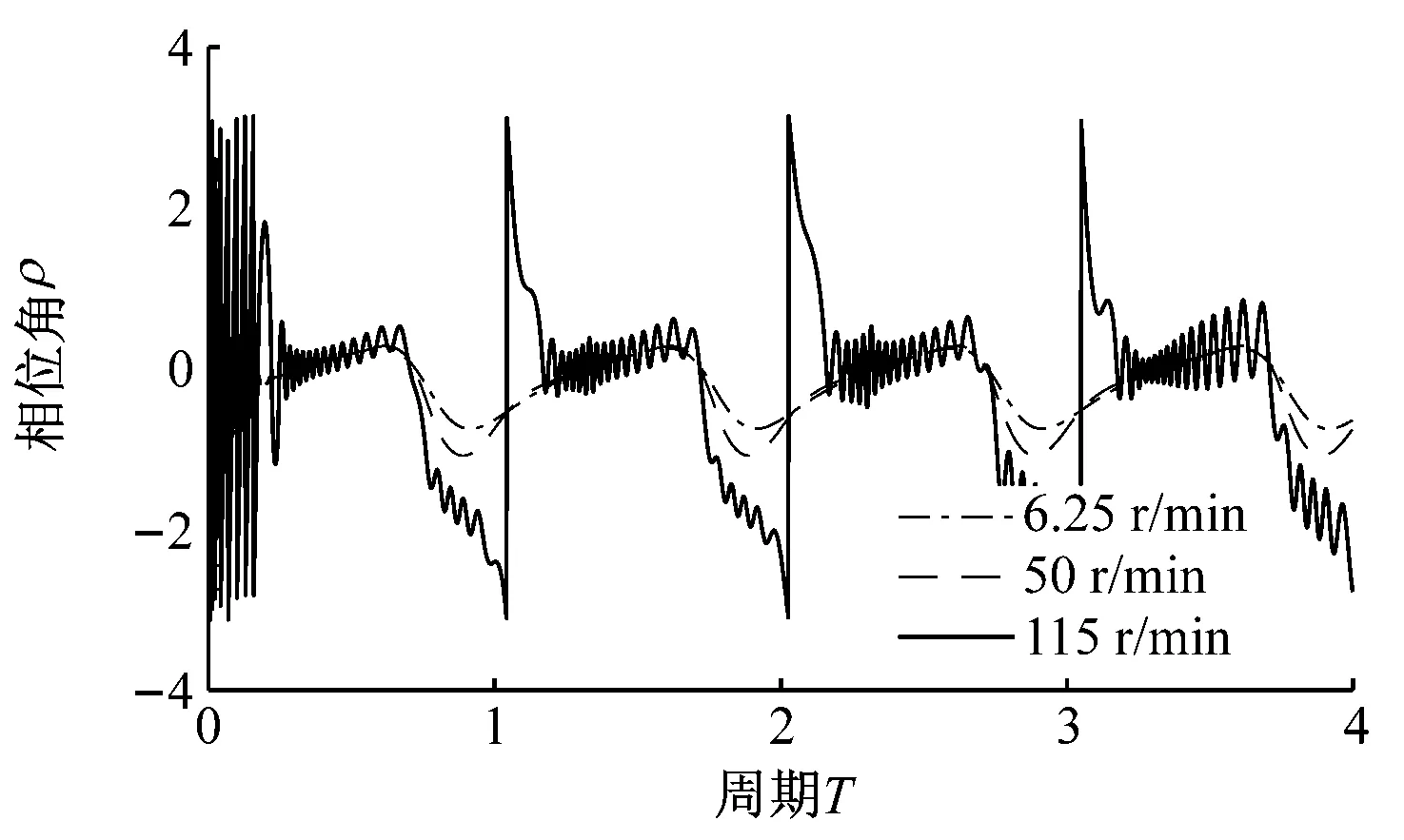
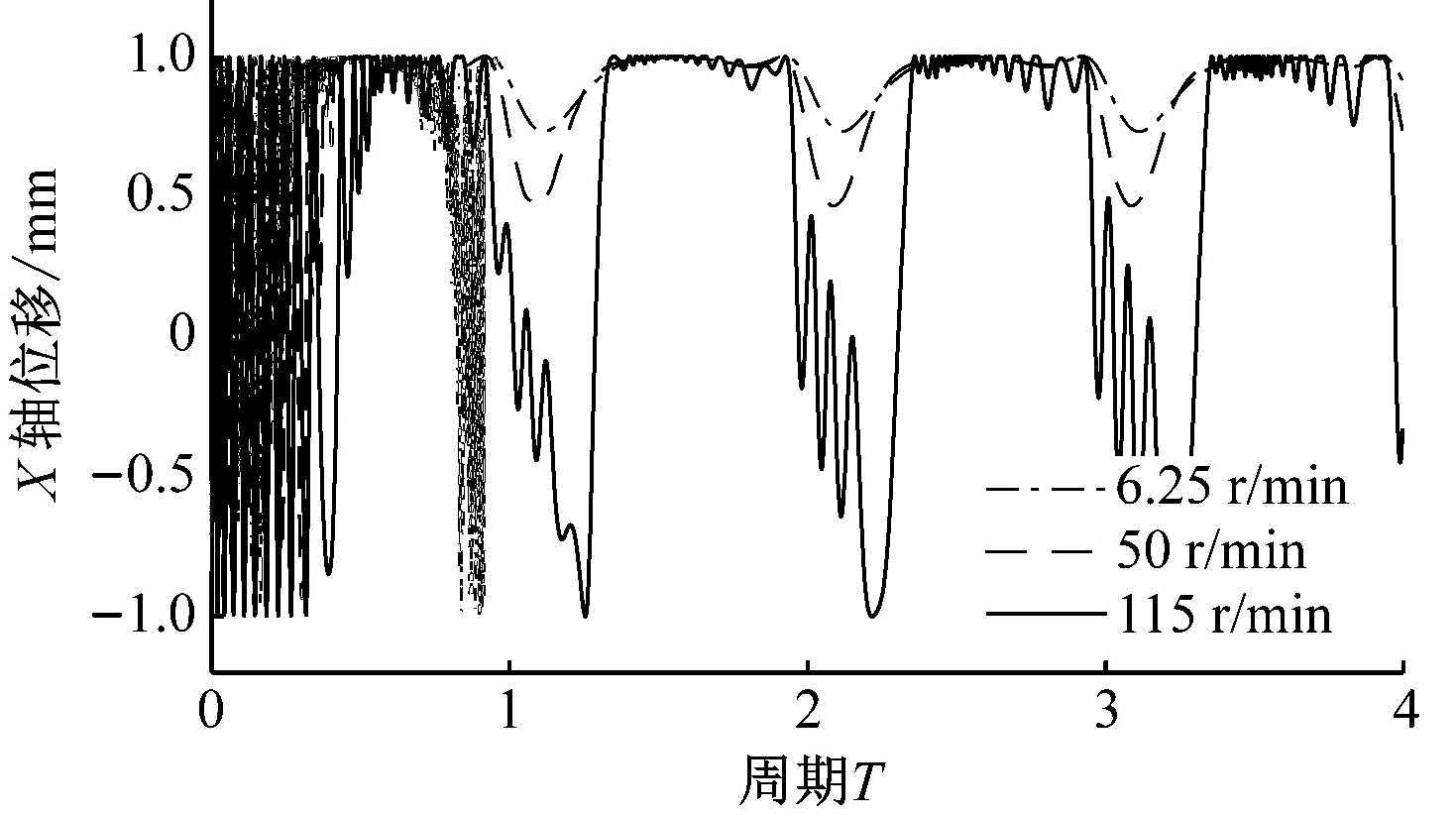
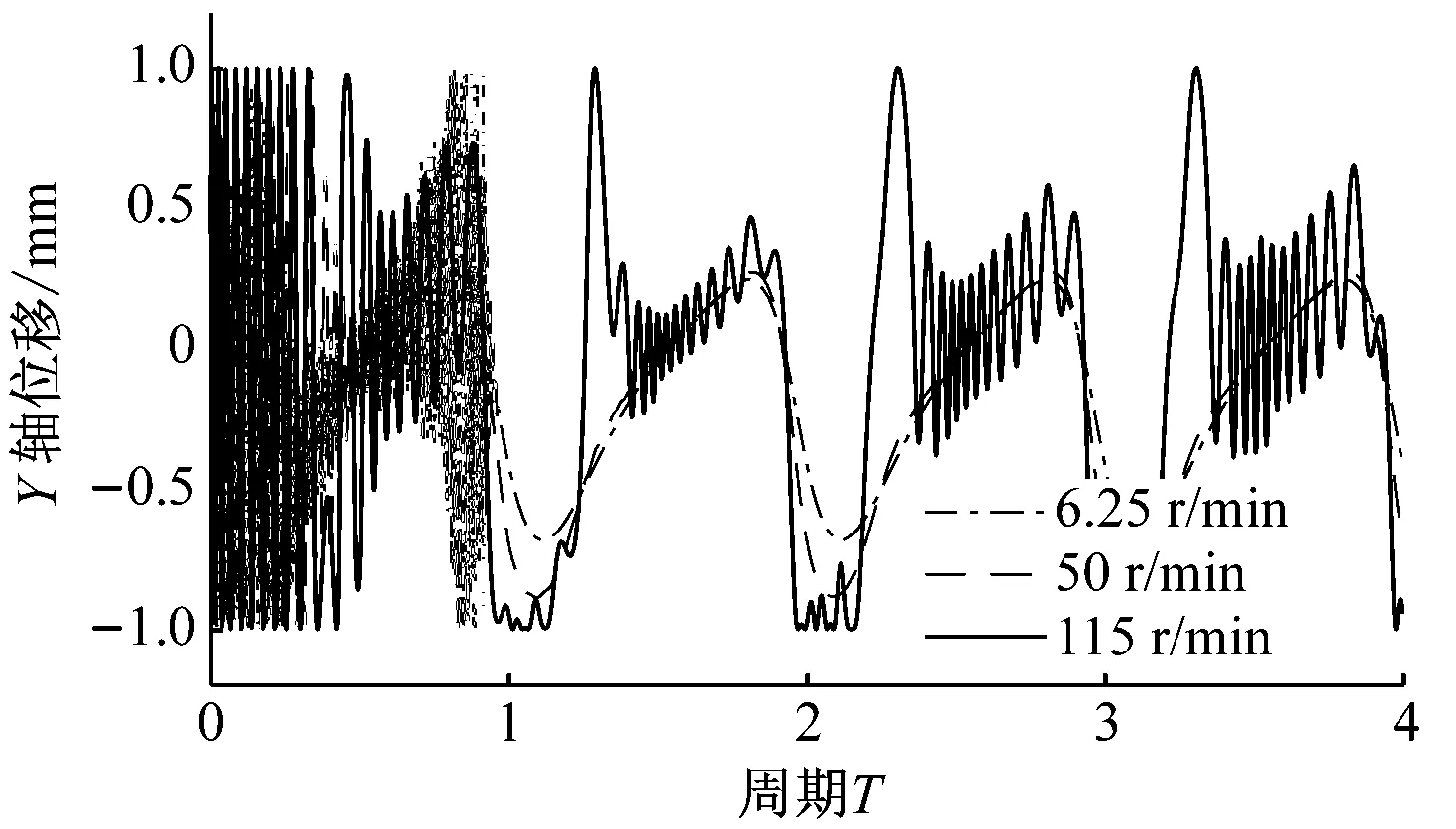
图5和图6分别为重力场加速度为1g，间隙为0.5 mm和1.0 mm的仿真结果。其X轴、Y轴位移，相位角变化和质心轨迹依旧遵从随曲柄转速增大，范围逐渐扩大的规律。

重力场加速度为1g情况下，三种间隙值的仿真结果均表现出曲柄转速不同，轴销质心运动轨迹差异明显。随曲柄转速增大，轴销质心轨迹由贴近轴套内表面右下部，逐步扩展至偏于右下的大部分位置，最终达到在整个间隙轴套内表面随机运动。

为了与已有的研究成果进行比较，图7给出了在重力环境下含间隙曲柄摇杆机构运动过程中间隙铰质心相位角变化对比结果。Tasora等以含间隙曲柄摇杆机构为研究对象，进行了间隙测量实验，并给出了仿真结果，其中，高速情况下间隙铰相位角变化仿真结果如图7(a)中曲线所示。对比不难看出，本文所建立的模型仿真结果与文献[20]仿真结果相比，相位角变化范围和变化趋势均较为相近，验证了本文建立的模型的有效性。

(a)

(b)

(c)

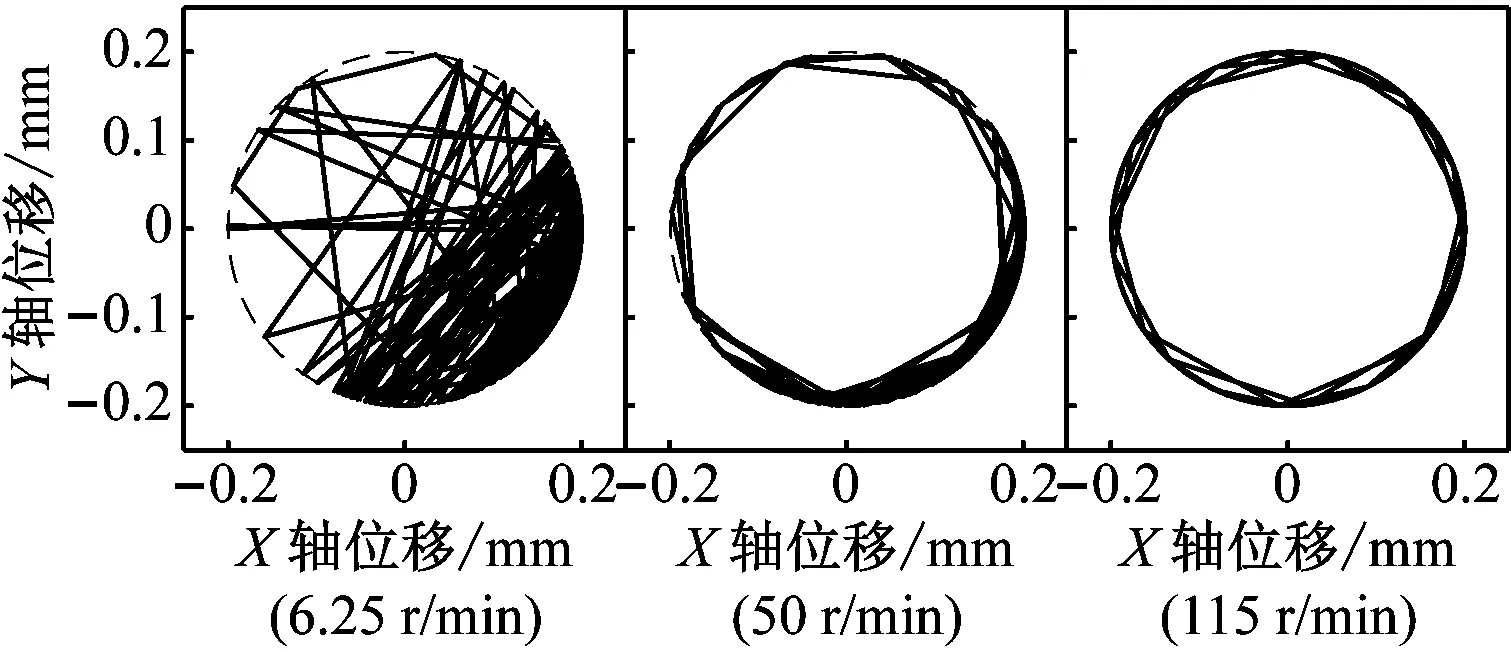
(d)图4 重力场加速度为1g，间隙为0.2 mm时的仿真结果Fig.4 The simulation results when the gravity is 1g, the clearance is 0.2 mm

(a)

(b)

(c)

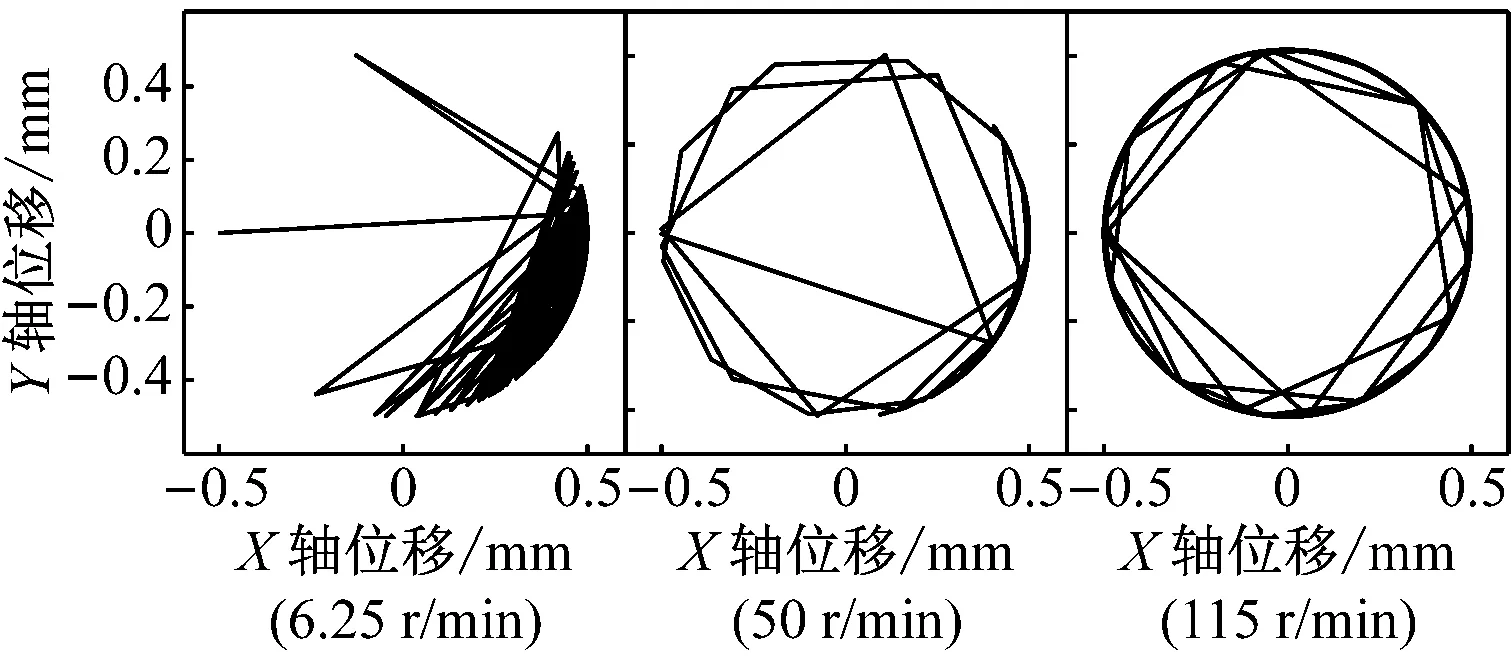
(d)图5 重力场加速度为1g，间隙为0.5 mm时的仿真结果Fig.5 The simulation results when the gravity is 1g, the clearance is 0.5 mm

2.2 重力场加速度为0时的仿真结果

图8为重力场加速度为0，间隙为0.2 mm条件下的仿真结果。X轴、Y轴位移和相位角变化仍能呈现出明显的周期性变化，但曲柄转速对其值的影响不大，低、中、高速的曲柄转速条件下，X轴、Y轴位移和相位角变化趋于一致。图8(d)的质心轨迹图显示，不同曲柄转速条件下，轴销质心均能实现在整个轴套内表面运动，且其运动相对连续，以至于图像显示轴销轨迹始终沿着轴套内表面。

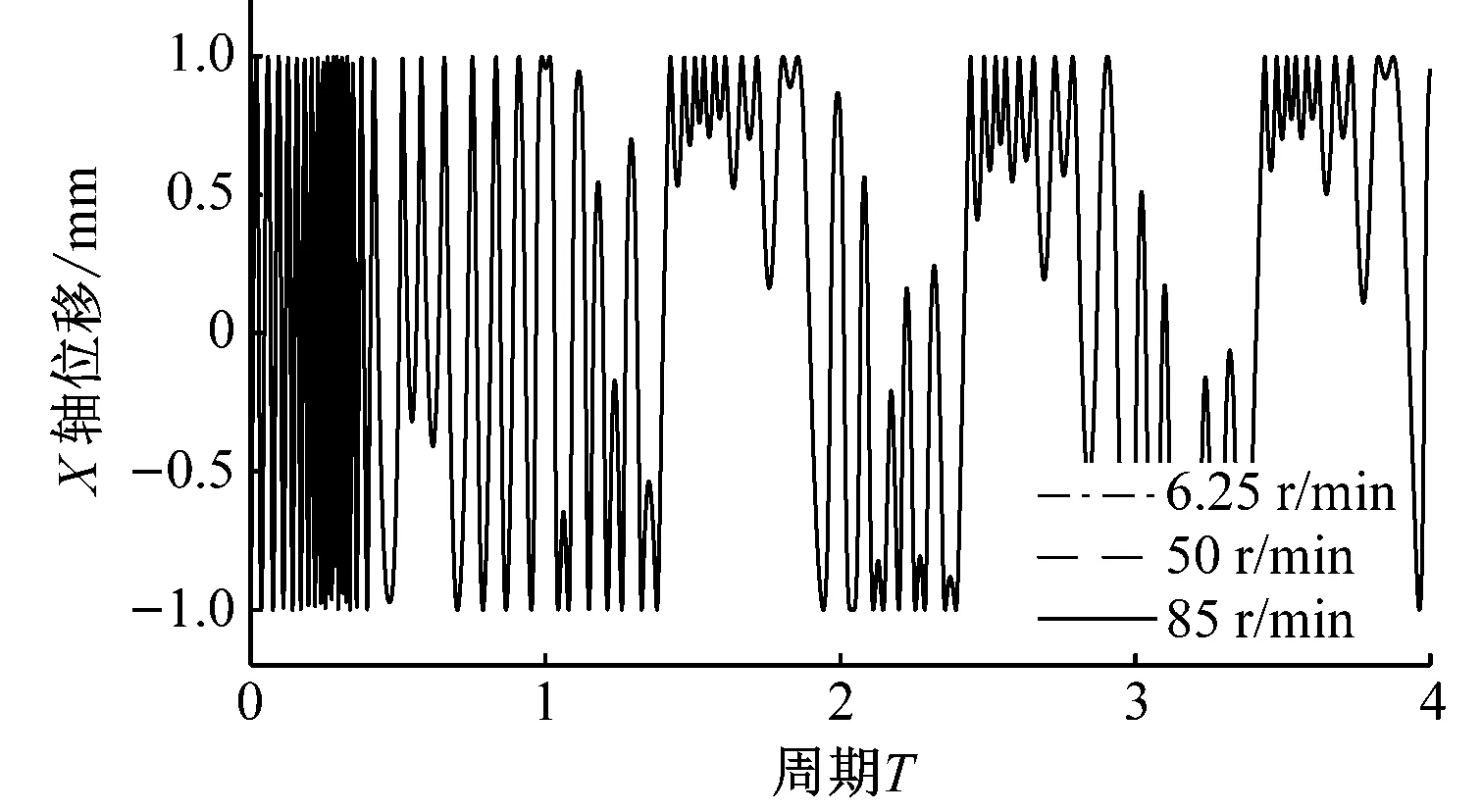
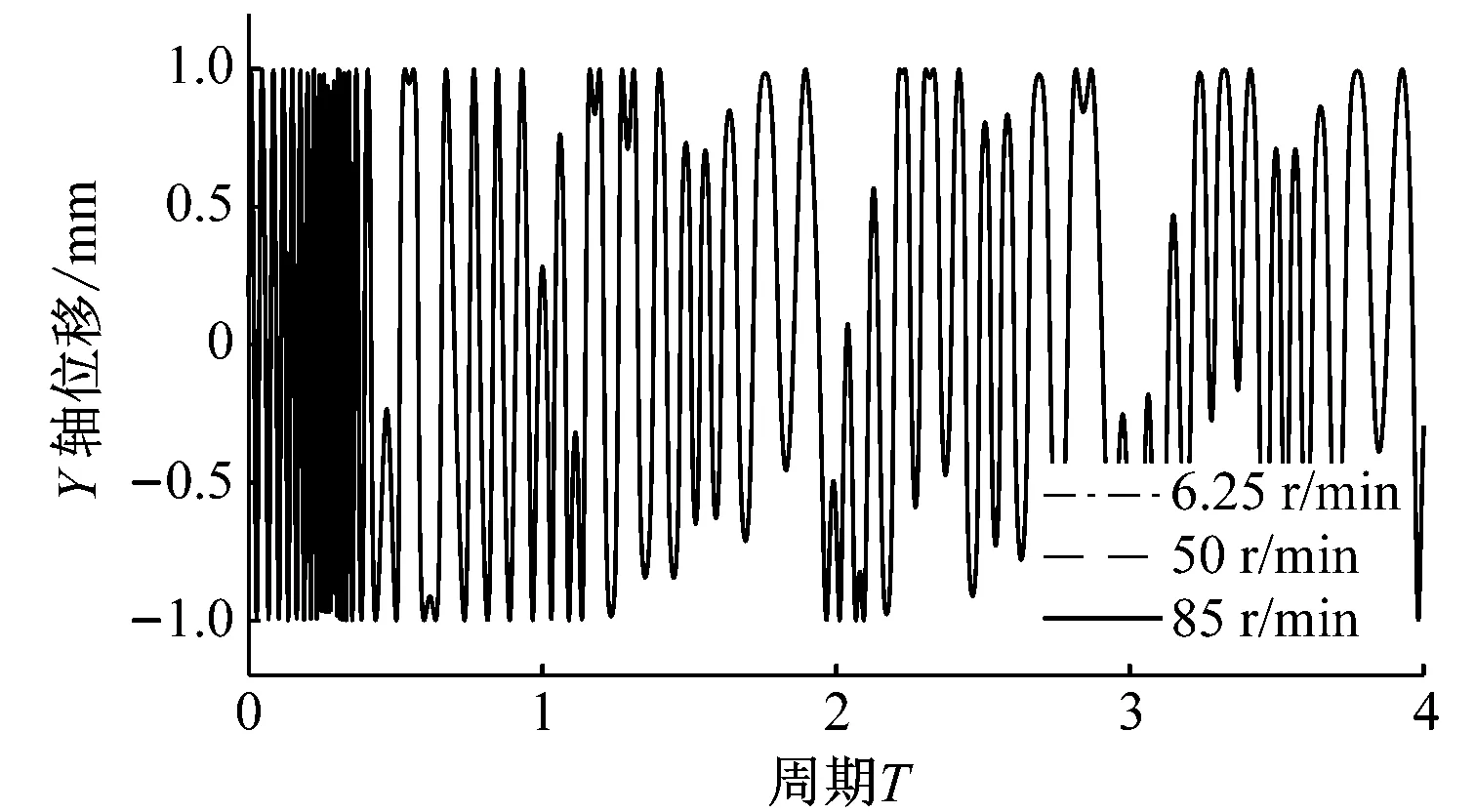
图9和图10分别是重力场加速度为0，间隙为0.5 mm和1 mm的仿真结果。X轴、Y轴位移和相位角变化仍能呈现出明显的周期性变化，且曲柄转速对其值的影响不大，低、中、高速的曲柄转速条件下，X轴、Y轴位移和相位角变化均基本一致。由图9(d)和图10(d)的质心轨迹图，不同曲柄转速条件下，轴销质心均能实现在整个轴套内表面运动，且运动轨迹几乎完全相同，但其运动随机性变大，质心轨迹不再是严格沿着轴套内表面运动。

(a)

(b)

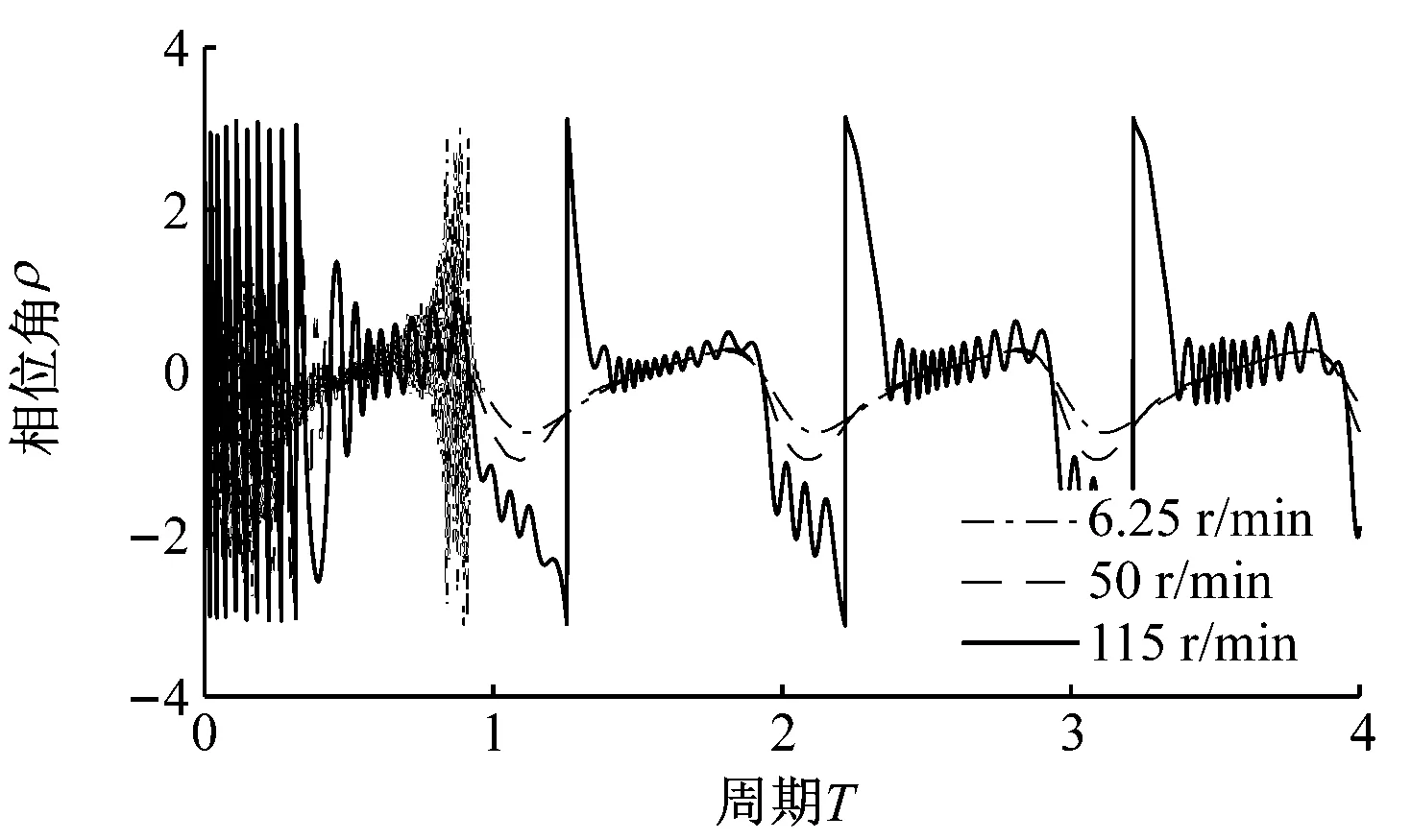
(c)

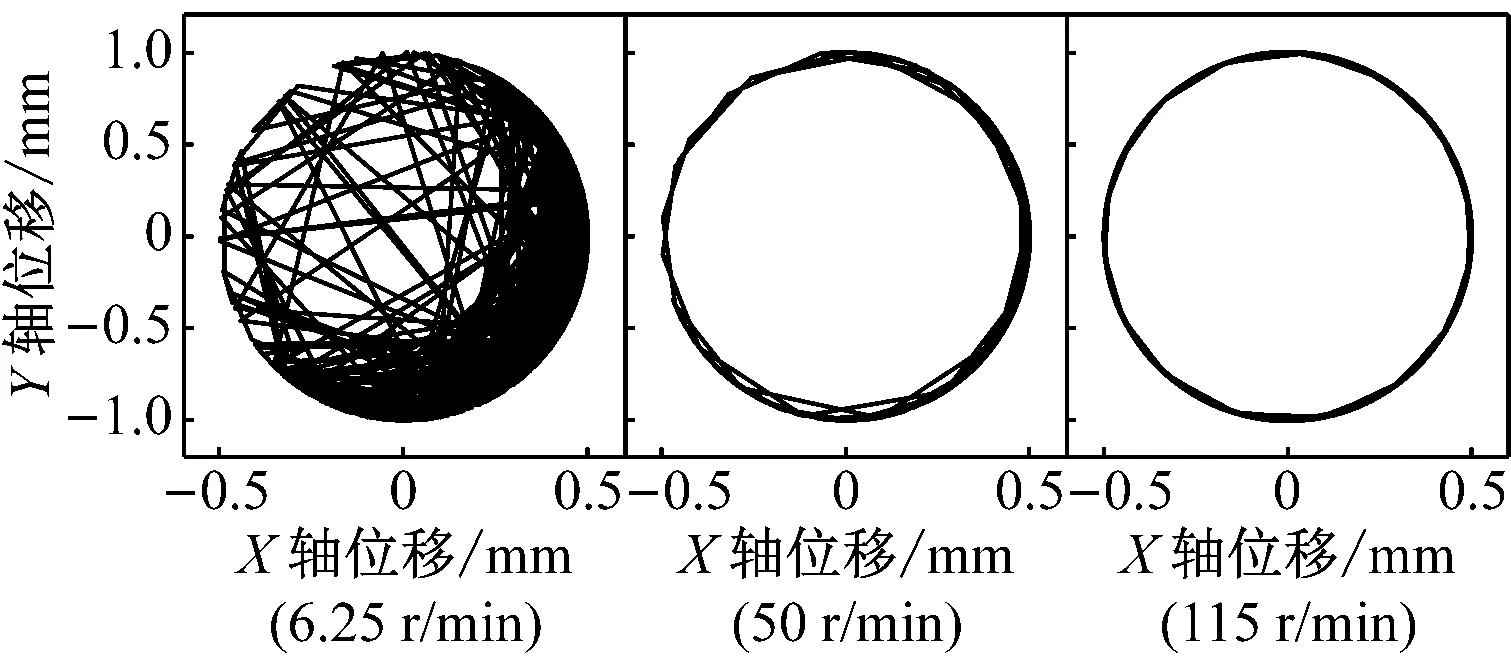
(d)图6 重力场加速度为1g，间隙为1 mm时的仿真结果Fig.6 The simulation results when the gravity is 1g, the clearance is 1 mm

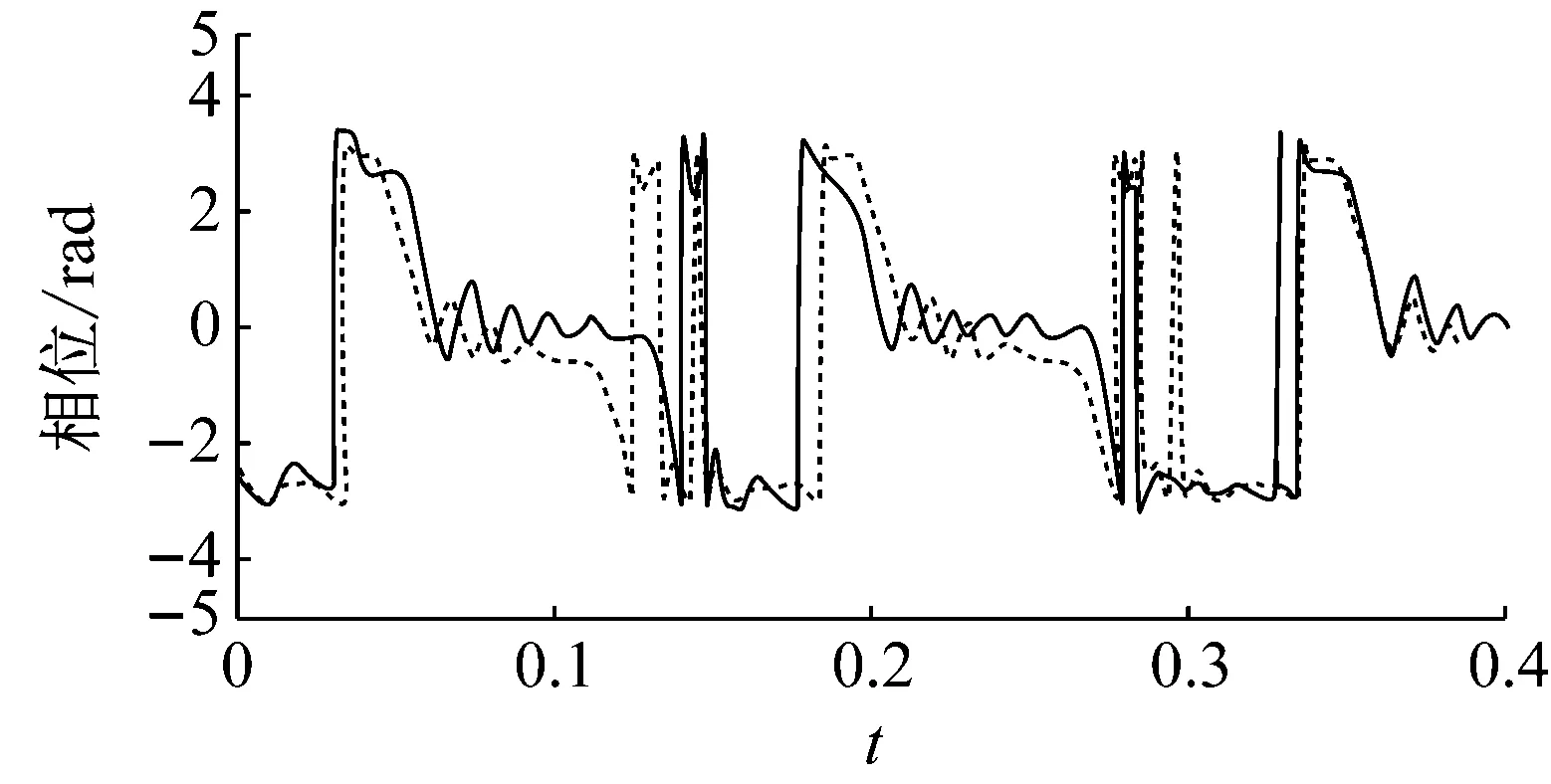
(a) 文献[20]数值仿真结果(虚线)

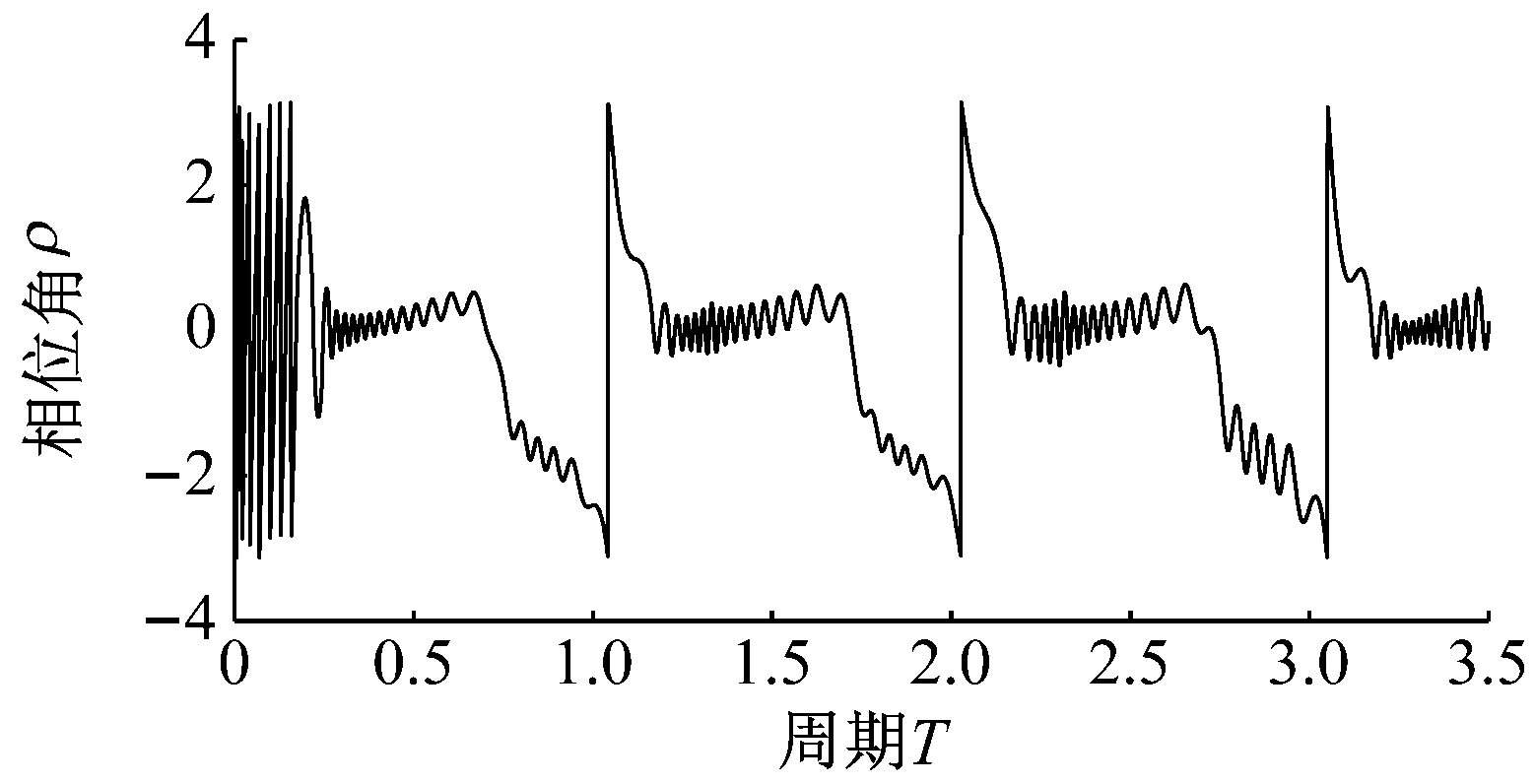
(b) 本文模型数值仿真结果图7 重力场加速度为1g条件下，含间隙曲柄摇杆机构间隙铰相位角变化对比图Fig.7 The difference of the phase angle of the clearance with the gravity is 1g

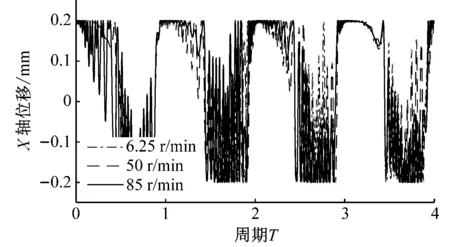
(a)

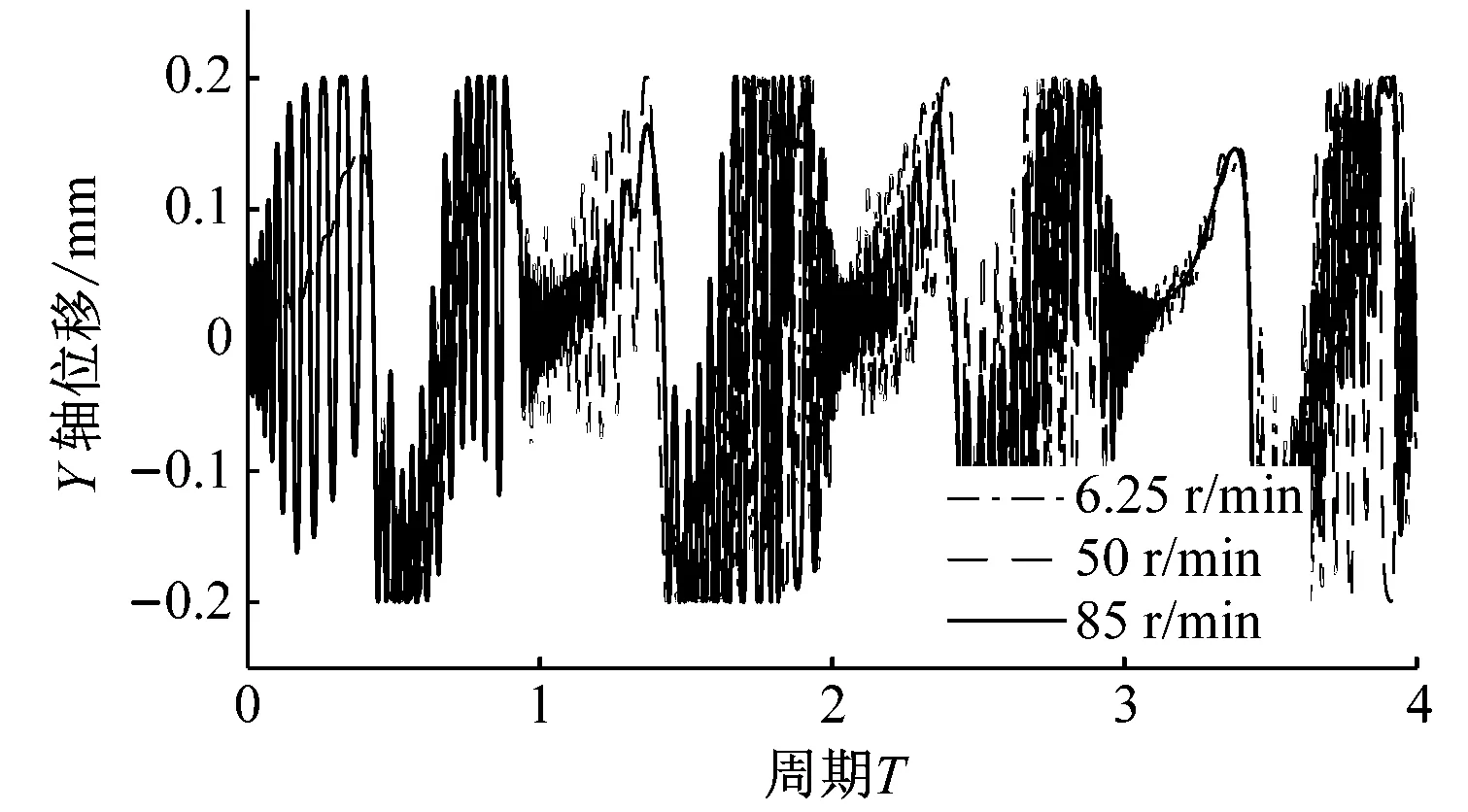
(b)

(c)

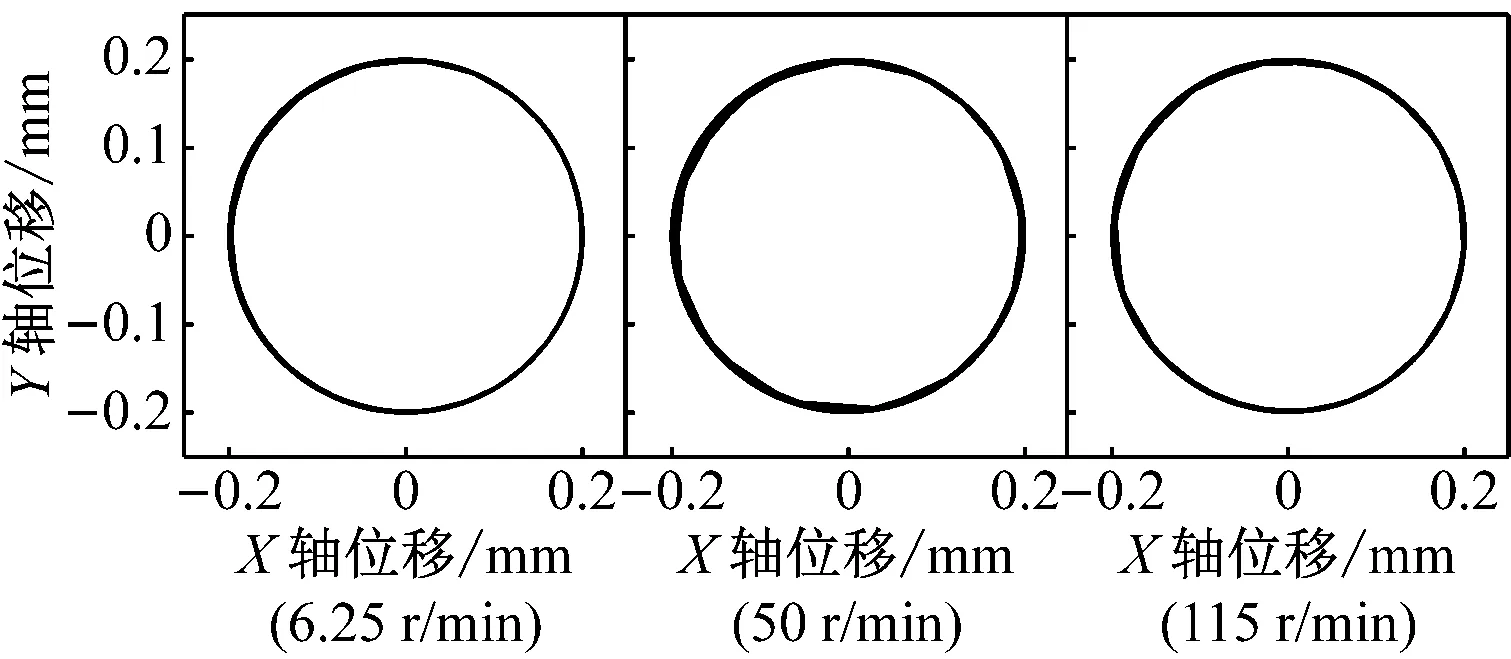
(d)图8 重力场加速度为0，间隙为0.2 mm时的仿真结果Fig.8 The simulation results when the gravity is 0, the clearance is 0.2 mm

(a)

(b)

(c)

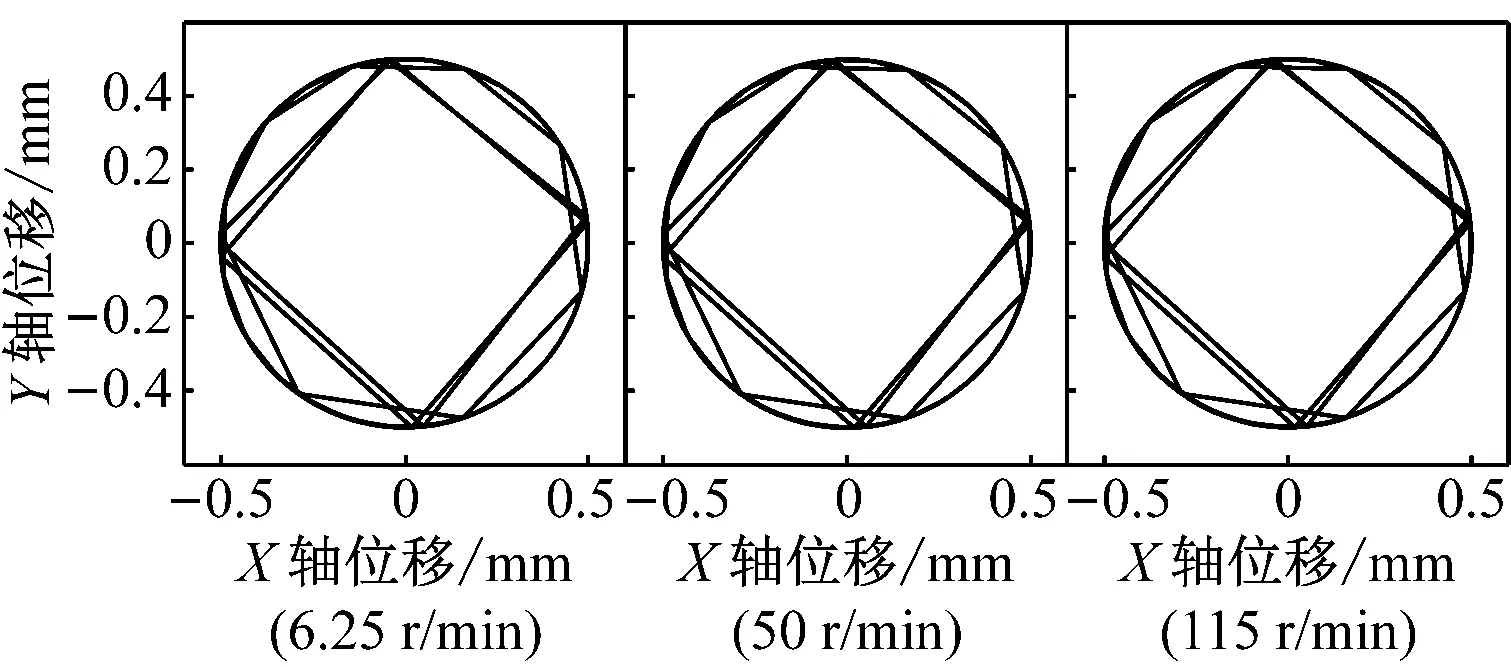
(d)图9 重力场加速度为0，间隙为0.5 mm时的仿真结果Fig.9 The simulation results when the gravity is 0, the clearance is 0.5 mm

(a)

(b)

(c)

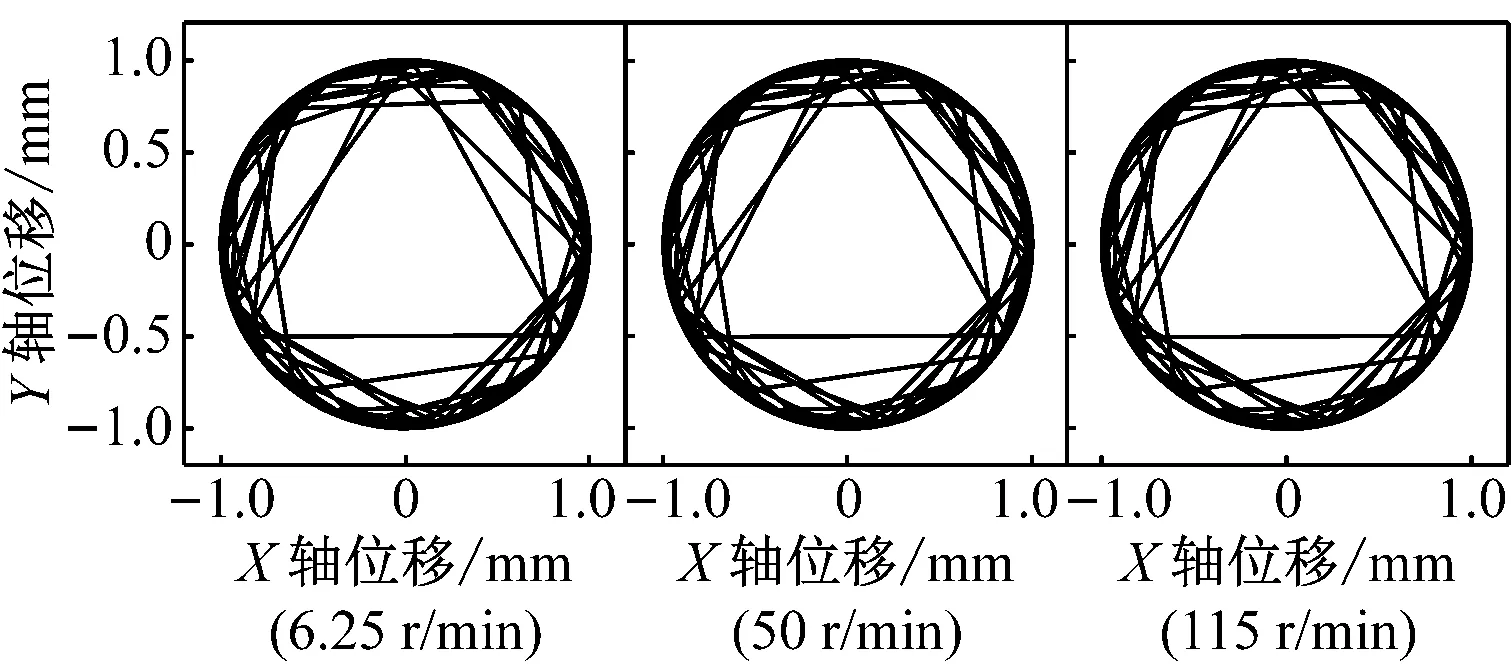
(d)图10 重力场加速度为0，间隙为1 mm时的仿真结果Fig.10 The simulation results when the gravity is 0, the clearance is 1 mm

3 结 论

本文以含间隙曲柄摇杆机构为例，基于含间隙旋转铰的连续接触等效模型，将间隙铰中轴销与轴套之间的半径间隙等效为无质量轻杆，推导了含间隙曲柄摇杆机构系统的动力学方程，并在ADAMS动力学仿真软件中建立含间隙曲柄摇杆机构模型，进行了地面重力环境和空间微重力环境下的数值仿真研究。仿真结果表明：在地面重力环境下，三种间隙值的仿真结果均表明，随曲柄转速增大，轴销质心轨迹由贴近轴套内表面右下部，逐步扩展至偏于右下的大部分位置，最终达到在整个间隙轴套内表面随机运动；在空间微重力环境下，含间隙旋转铰径向间隙方向不受重力影响，因此无论低速还是高速运行，质心运动轨迹均在整个轴套范围内，且随着间隙值的增大，轴销运动随机性也逐渐变大，质心轨迹不再是严格沿着轴套内表面运动。需要注意的是，本文间隙等效模型采用的是无质量轻杆，建模时忽略了轴销和轴套接触表面的形变及各种干扰，主要体现了含间隙旋转铰在运动学方面性能，难以描述运动副元素间的动力学特性。下一步我们将进行不同重力环境下含间隙机构间隙测量实验研究，并与仿真结果进行对比分析。