Noor III光热电站吸热塔气动阻尼研究

黄景辉， 李寿英， 刘 敏， 陈政清， 回 忆， 李红星

(1. 湖南大学 风工程与桥梁工程湖南省重点实验室，长沙 410082；2. 西北电力设计研究院，西安 710000)

光热电站吸热塔是典型的高耸结构，高耸结构在来流风作用下同时存在顺风向和横风向振动，当结构在横风向产生涡激振动时，结构的横风向风振有时会占主要地位。西安大略大学试验结果表明吸热塔在设计风速下的位移值超过规范值的40%左右，而且该结构的涡振临界风速小于设计风速，且涡振区响应起控制作用。

涡激振动是一种具有自激性质的限幅振动，虽然涡激振动不像颤振、驰振一样会引起发散性的振动，但是由于低风速下很容易发生而且当旋涡脱落频率接近结构的自振频率时，横风向响应会显著增加，产生所谓的涡激共振现象。涡激共振主要对桥梁、高耸结构等细长结构的破坏作用较大，由涡激共振引起的振动幅度足以影响结构的安全性和舒适度[1-2]。

目前，高耸结构的涡激振动现象已经得到很多国内外学者的广泛研究。1994年，同济大学顾明等[3]对东方明珠电视塔进行了气弹模型试验，发现风速在30 m/s时，结构10 m高度处的加速度突然增大，经研究分析为涡激共振导致。2003年，东南大学石启印等[4]对首都机场新塔台建筑进行研究，发现当风速为31.7 m/s左右时，加速度响应均方根值突然增大。这是因为塔台上部变截面处的旋涡脱落频率和结构的第五阶固有频率相等从而引起涡激共振导致的。

对涡振区气动阻尼识别属于模态参数识别的一部分，模态分析试验分为环境振动试验、自由振动试验和强迫振动试验。环境振动试验模态分析的方法有峰值法(Peak Picking，PP)，增强型频域分解法(Enhanced Frequency Domain Decomposition，EFDD)[5]，自然激励技术(Natural Excitation Technique，NExT)[6]，随机子空间法(Stochastic Subspace Identification，SSI)[7]，随机减量法(Random Decrement Technique，RDT)，最小二乘复频域法(Least-Squares Complex Frequency-Domain Method，p-LSCF)[8]和广义卡尔曼滤波法(Extended Kalman Filter，EKF)等。在进行高层建筑气动阻尼识别时，随机减量法是一种已经被工程研究人员广泛应用且认可的方法[9]；广义卡尔曼滤波法作为一种较新的方法，抗噪声能力强，可用于非线性系统的参数识别,提高了气动阻尼识别的精度。因此本文采用随机减量法和广义卡尔曼滤波法对不同风速下的模态阻尼进行识别。

随机减量法由Cole在1973年进行航天飞机结构试验时首次提出。此后，Ibrahim等[10-11]将该方法进行了扩展并从数学角度进行了论述。全涌等[12]对长细比为6的方形断面柱体单自由度气动弹性模型进行了风洞试验，利用随机减量法对这类高层建筑的横风向及顺风向气动阻尼进行了识别研究。

卡尔曼滤波法由Kalman[13]在1960年提出。由于实际系统的非线性特点，Jazwinski[14]采用等效线性化的近似方法，提出了广义卡尔曼滤波法，这种方法是基于最小方差准则下的一种滤波方法，解决了非线性系统的滤波问题。Pan等[15]通过对3自由度剪切型结构和2层平面框架结构进行仿真，验证了该方法的有效性。

为此，分别运用随机减量法和广义卡尔曼滤波法，在不同结构阻尼比(0.7%和1.0%)下对不同风速下的气动阻尼进行识别，以对吸热塔的设计和减振分析提供参数依据。

1 项目背景及模型介绍

Noor III光热电站吸热塔位于非洲摩洛哥，如图1所示，地面以上高度243 m，为圆形变截面结构，外径从底面的23 m变化到顶部的20 m。0～200 m高度范围内为混凝土结构，壁厚从底部的800 mm，变化到顶部的450 mm，200～243 m高度范围内为钢结构，为目前全球规模最大的太阳能光热电站。根据实际结构参数和相似准则制作了吸热塔气弹模型，如图2所示。模型的几何缩尺比一般是通过自然风湍流积分尺度和风洞来流湍流积分尺度的比值来确定，同时要考虑堵塞效应和避面效应的影响，综合考虑后确定的模型几何缩尺比为1/200。模型制作材料采用704a铝合金，模型总高度1.2 m。

图2 吸热塔气弹模型Fig.2 Aeroelastic model of the tower

2 风场调试与实验仪器介绍

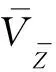
(1)

(2)

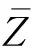
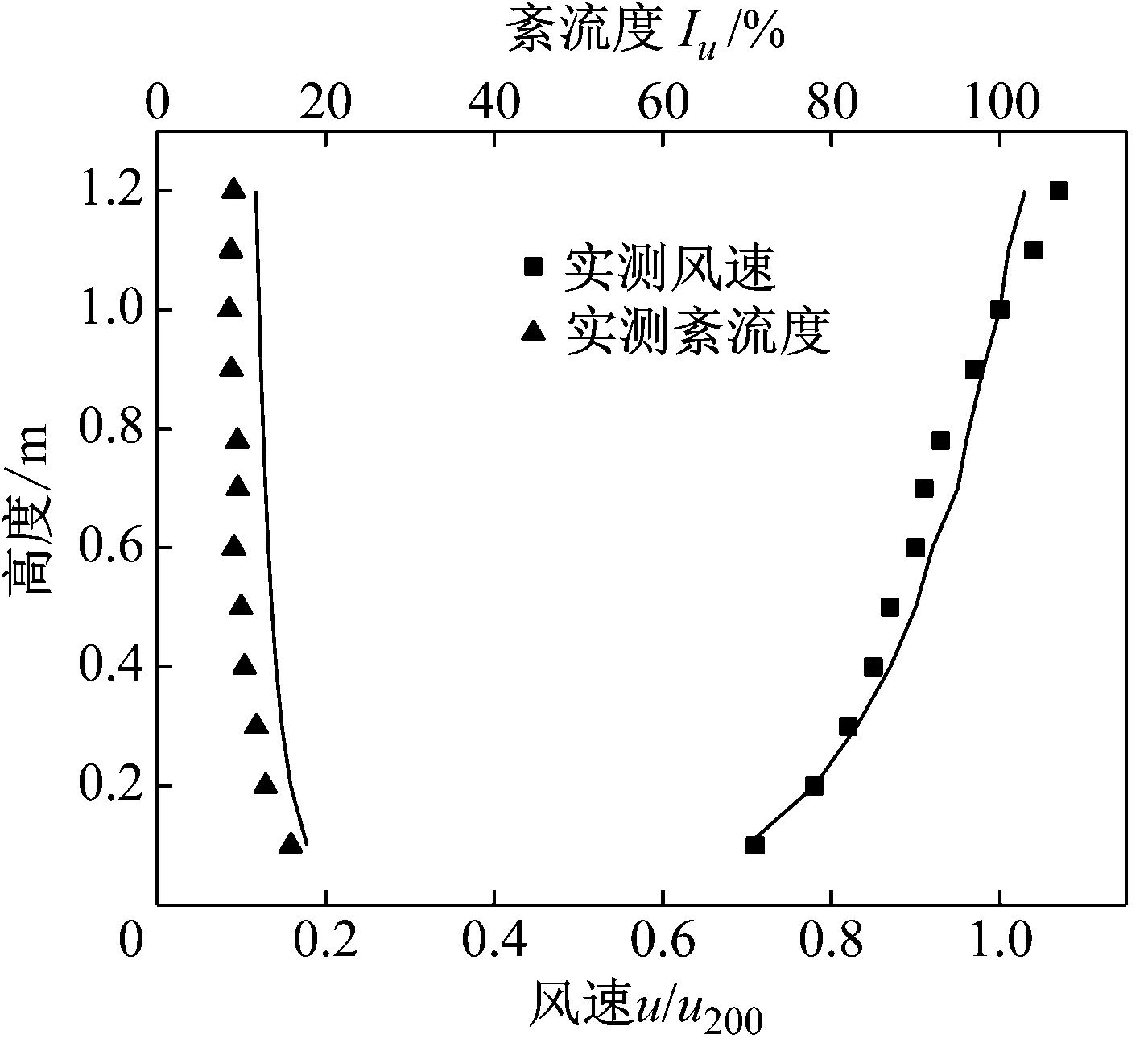
图3 湍流度剖面和平均风剖面Fig.3 Turbulence intensity and mean wind speed profiles

本试验在湖南大学HD-2大气边界层风洞高速试验段进行，高速试验段尺寸为17 m×3 m×2.5 m，风速0～60 m/s连续可调，如图4所示。

图4 湖南大学HD-2大气边界层风洞Fig.4 Atmospheric boundary layer wind tunnel at Hunan University

试验选用的测量系统为江苏东华测试技术有限公司生产的DH5920动态信号测试系统，可实现16通道电压、电荷及传感器信号的同步采集。

试验选用的加速度传感器为河北秦皇岛朗斯测试技术有限公司研制的LC0408T型压电式加速度计，频率范围1～18 000 Hz，灵敏度为5.11 PC/g，单个传感器质量为2.8 g。

3 模型的相似系数

对气弹模型，除了要满足几何相似外，还要满足气动弹性相似，主要由Reynolds数、Froud数、Strouhal数、Cauchy数、密度数和阻尼比6个无量纲参数决定。表1为实际结构与风洞模型之间应该满足的一致性条件。

表1 无量纲参数相似要求Tab.1 Similarity requirements of dimensionless parameters

在本气弹模型设计中，因为结构模型风洞试验首先进行了几何缩尺，导致Reynolds数相似性很难实现，对于高耸结构来说，雷诺数有不可忽略的影响，在后续工作中，应该采取增加表面粗糙度的措施来研究这一影响。

Froud数反映了重力场对风振的影响，只有对P-Δ效应显著的重力场风振响应才有一定的影响，本文主要研究结构水平方向的响应，因此放松了对该参数的模拟。气弹模型应该满足的相似比如表2所示，其中n为几何缩尺比，m为风速比。

表2 气弹模型相似比Tab.2 Similarity ratio of the aeroelastic model

由表2可知，刚度相似比不但与几何缩尺比n有关系，还和风速比m有关系，因此在模型设计时先初选一个风速比1/5，然后通过模型动力标定试验确定最终的风速比。确定方法为通过模型的实测频率确定模型的实测频率比λf，然后由λf=n/m反算出最终的风速比。

4 模型动力特性标定

通过人工推模型的方式获得横风向加速度衰减曲线并对其做FFT进行频谱分析。结果分别如图5和图6所示。

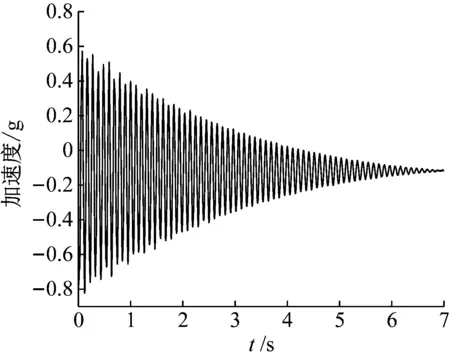
图5 加速度衰减曲线Fig.5 Acceleration attenuation curve

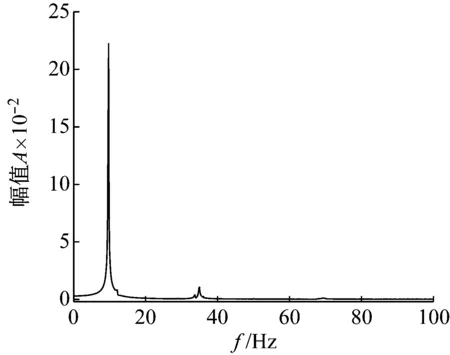
图6 横风向加速度谱Fig.6 Across-wind acceleration spectra

由加速度频谱分析可知，模型的振动主要集中在第一阶振型上，其它模态的贡献比较小。由频谱图可得模型的第一阶振动频率为9.71 Hz。

通过ANSYS有限元模型对模型振型进行验证，模型的第一阶振型如图7所示。模型的实测振型与ANSYS模拟振型结果吻合较好。因为第一阶振型占主要作用，所以满足试验要求。

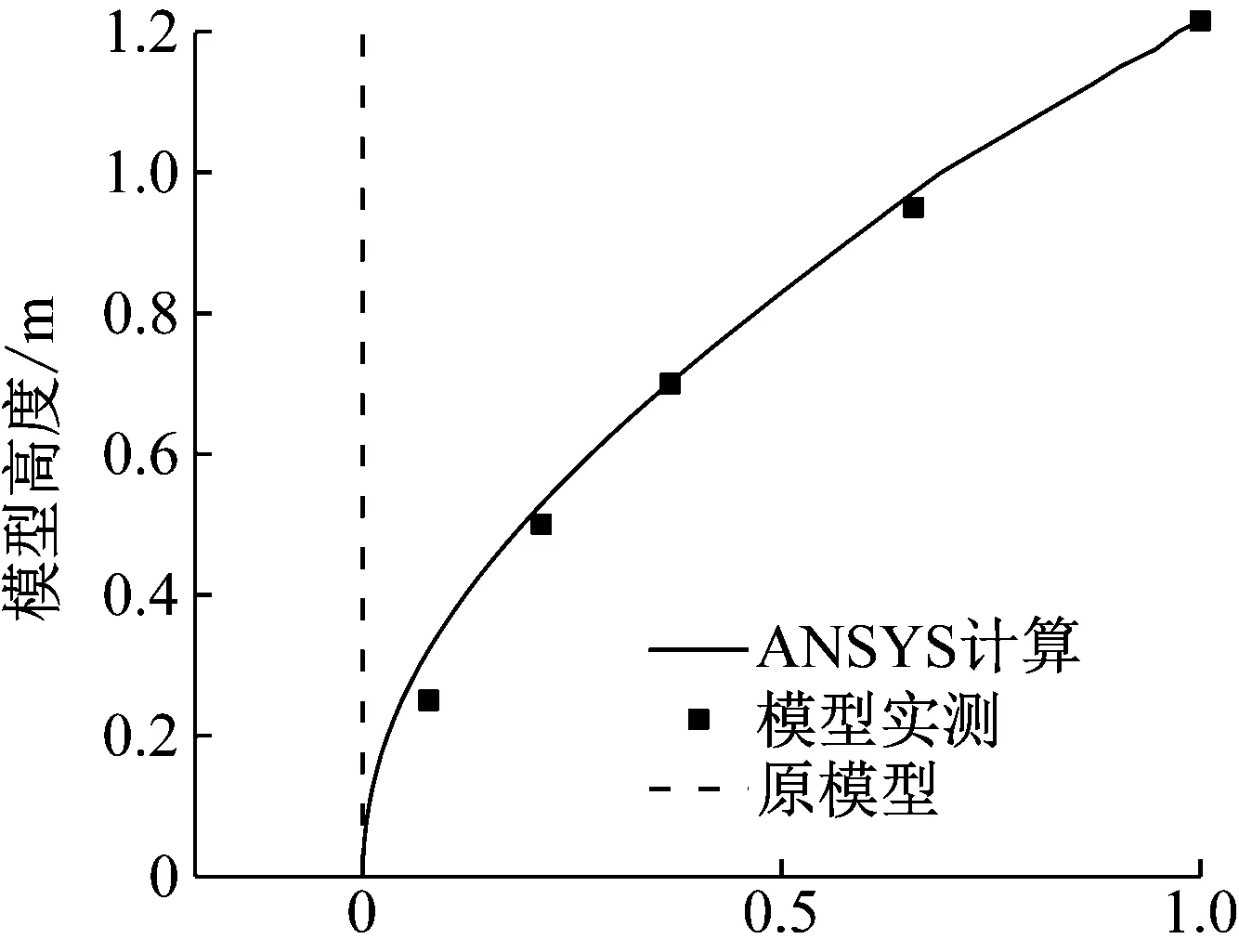
图7 模型第一阶振型Fig.7 First order modal shape

实际结构的第一阶振动频率为0.28 Hz，模型的第一阶振动频率为9.71 Hz，频率比为34.7，根据第一阶频率比将风速比调整为1/5.77，最终的模型参数相似比见表2。

5 涡激振动的气动负阻尼现象

当流体流过钝体时，会在物面产生大范围的边界层分离并形成宽阔尾流，常伴有旋涡脱落现象。在最简单的漩涡脱落形式中，结构背面形成摇摆旋涡形式的稳定涡街，如图8所示。

图8 卡门涡街Fig.8 Von Karman vortex street

当旋涡脱落频率ns与横风向结构振动特征频率ne相同时，可能会产生强烈的振动。因此，由ne=ns定义的临界风速Ucrit为

Ucrit=ned/St

(3)

式中：St为斯托罗哈数；d为模型直径；对圆形截面St=0.2；结构的第一阶自振频率ne=9.71 Hz。

由此求得涡振临界风速Ucrit=5 m/s，涡激共振区间估算为Ucrit～1.3Ucrit，即5～6.6 m/s,试验时将5～7 m/s的风速进行加密测量。

涡激振动现象要通过专门的气动弹性试验来进行研究。气动弹性问题是一个复杂的耦合问题，常常用气动阻尼来描述这一现象对风效应的影响。

以单自由度体系为例，在风场中其运动方程可以表示为

(4)

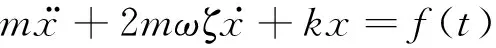
(5)

式中：ζ=ζs+ζa为结构阻尼比与气动阻尼比的总和；f(t)为作用在结构上的静风力。

横风向气动阻尼较为复杂，在涡脱频率临近结构自振频率时，气动阻尼会突然从较大的正阻尼变为较大的负阻尼，从而大大增加结构的横风向响应。所以，准确识别涡振区的横风向气动阻尼对分析和控制结构振动具有重要意义。

6 气动阻尼识别

6.1 气动阻尼识别原理

本次试验分别运用随机减量法和广义卡尔曼滤波法对气动阻尼进行识别。

随机减量法通过对加速度子样本函数的多次叠加来消除初速度和外部激励的影响，最终得到由初位移引起的自由衰减信号。

然后运用时域识别方法便可以从自由衰减信号中识别出系统的频率及阻尼等模态参数。随机减量法的原理如图9和图10所示。

图9 样本函数截取示意Fig.9 Intercept of sample functions

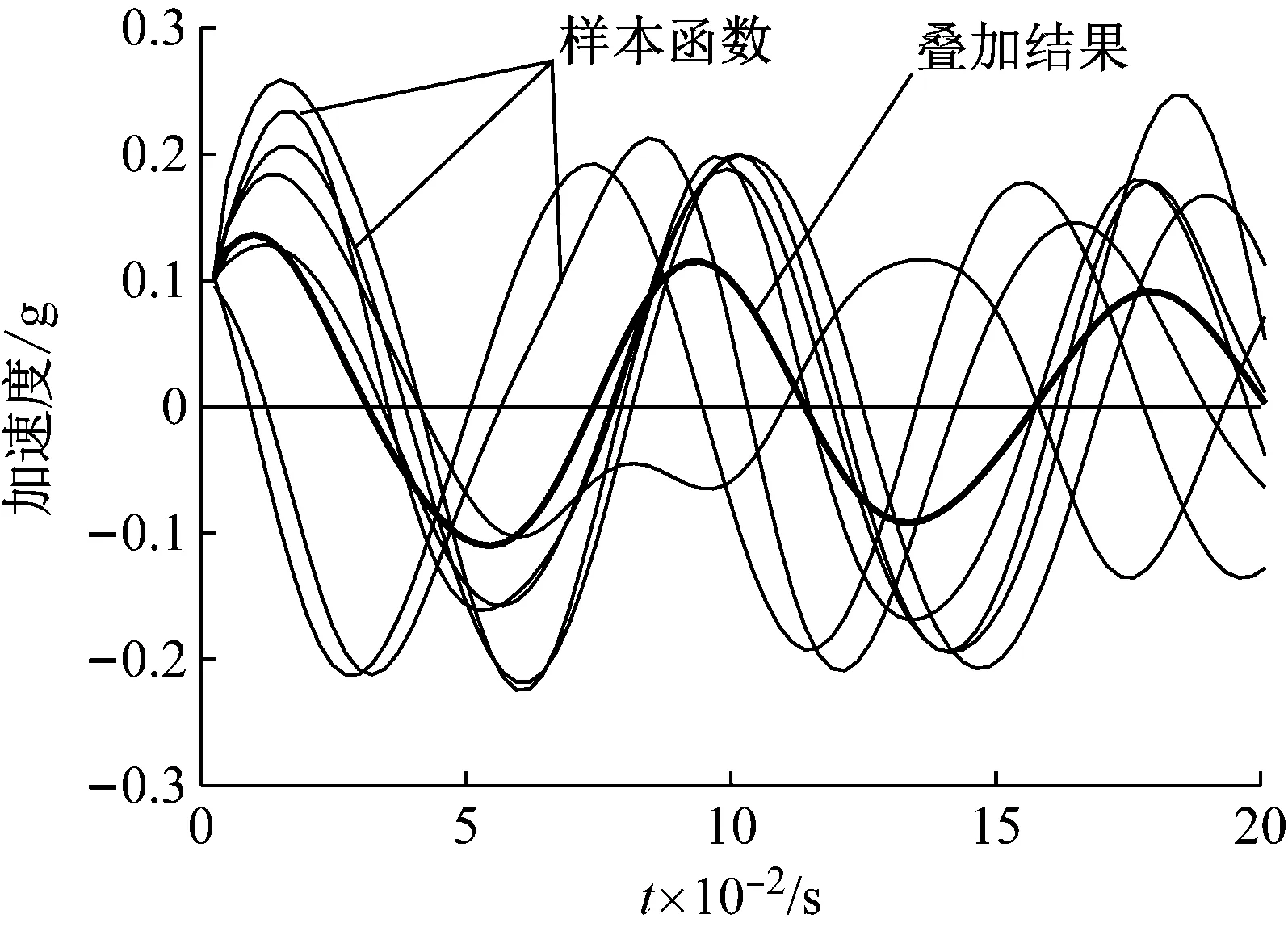
图10 样本函数叠加示意Fig.10 Superposition of sample functions

卡尔曼滤波法是用线性随机差分方程描述离散时间随机过程，基于状态空间法和正交投影理论提出的新的滤波理论及算法。其滤波方程是一组递推公式，计算过程是一个不断预测、修正的过程。卡尔曼滤波器应用广泛且功能强大：它可以估计信号的过去和当前状态，甚至能估计将来的状态，即使并不知道模型的确切性质。

6.2 气动阻尼识别过程

以随机减量法为例，介绍气动阻尼的识别过程，运用Matlab程序对原始数据进行处理。

将原始数据导入，得到风速6 m/s，结构阻尼比0.7%下的加速度信号图。对原始信号进行去多项式和低通滤波处理，截止频率为9.8 Hz，得到滤波后的数据。数据采样时间超过15 min，采样频率为1 000 Hz。图11、图12分别为500～600 s和550～560 s的加速度信号图。图中数据具有明显的涡振特征，说明了数据的有效性，可以用于涡振参数识别。

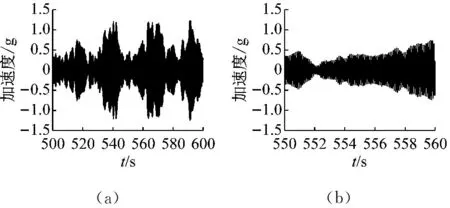
图11 原始信号Fig.11 Original signal

图12 滤波信号Fig.12 Filtered signal

在进行随机减量样本函数提取时，一个关键性问题是信号截取幅值的选取。因为信号长度一般是一定的，但是当截取阈值取的越大，截取的子信号段数将会减少，这样会使有效的平均次数减少，平均效果变差；相反，如果截取的阈值过小，虽然平均的次数增多了，但是由于小幅值产生的激振量小，平均效果也会很差。所以在实际应用中，既要保证适当大的截取阈值又要保证一定数量的平均次数，显然在这个相互矛盾的问题中需要提出一种更好的改进方法。2000年，张西宁等[16]提出一种正、负阈值同时截取的信号提取方法。具体操作方法是：用绝对值相等的正负阈值分别截取随机减量信号，由于截取的意义相同，负阈值截取以后的信号经过变号后可直接参与叠加平均，这样使得参与平均的样本函数数量增加，最后提取随机特征信号的质量也得到了提高，并且通过数学方法证明了该改进方法。

在本次试验数据的处理过程中，截取幅值为1.25 倍的时程数据的标准差，经过叠加后得到自由衰减曲线，截取自由衰减曲线的部分结果如图13所示。

当得到自由衰减曲线后，可以运用下列公式进行总阻尼比的计算

(6)

图13 部分自由衰减曲线Fig.13 Partial free decay curve

式中：ζ为总阻尼比；μP为开始加速度振幅；μQ为结束加速度振幅；N为μP与μQ之间的周期数，这里取N为20。

结构阻尼比0.7%，风速6 m/s时用随机减量法识别出的总阻尼比平均值为0.13%，此工况下用广义卡尔曼滤波法识别出的总阻尼比为0.16%。

6.3 不同加速度幅值处的阻尼识别

选取不同的加速度幅值作为μP进行总阻尼比识别，研究加速度幅值对总阻尼比识别的影响，结构阻尼比0.7%，风速6 m/s时的结果如图14所示。从图中可以得出，总阻尼比具有随加速度幅值的增大先增大后减小的规律。

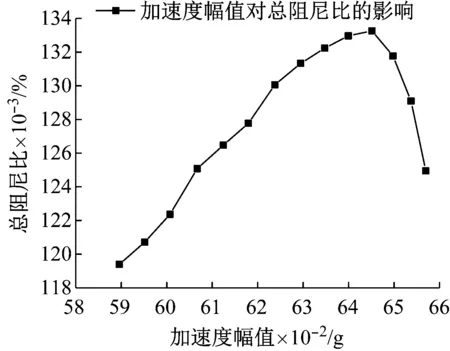
图14 不同加速度幅值处识别的总阻尼比Fig.14 Total damping ratios identified at different acceleration amplitudes

6.4 气动阻尼识别结果汇总与比较

运用随机减量法和广义卡尔曼滤波法对结构阻尼比0.7%下的气动阻尼进行识别，将结果进行了对比验证。不同风速下两种方法的阻尼比识别结果如表3、图15和图16所示。从中可以看出两种方法的识别结果可以较好地相互验证，说明了所用方法的可靠性。

结构阻尼比0.7%和结构阻尼比1%下运用随机减量法对气动阻尼的识别结果如图17所示。结构阻尼比增大后气动阻尼比全部变为负值且有整体增大的趋势。

将两种结构阻尼比下的加速度均方根值表示在图18中。

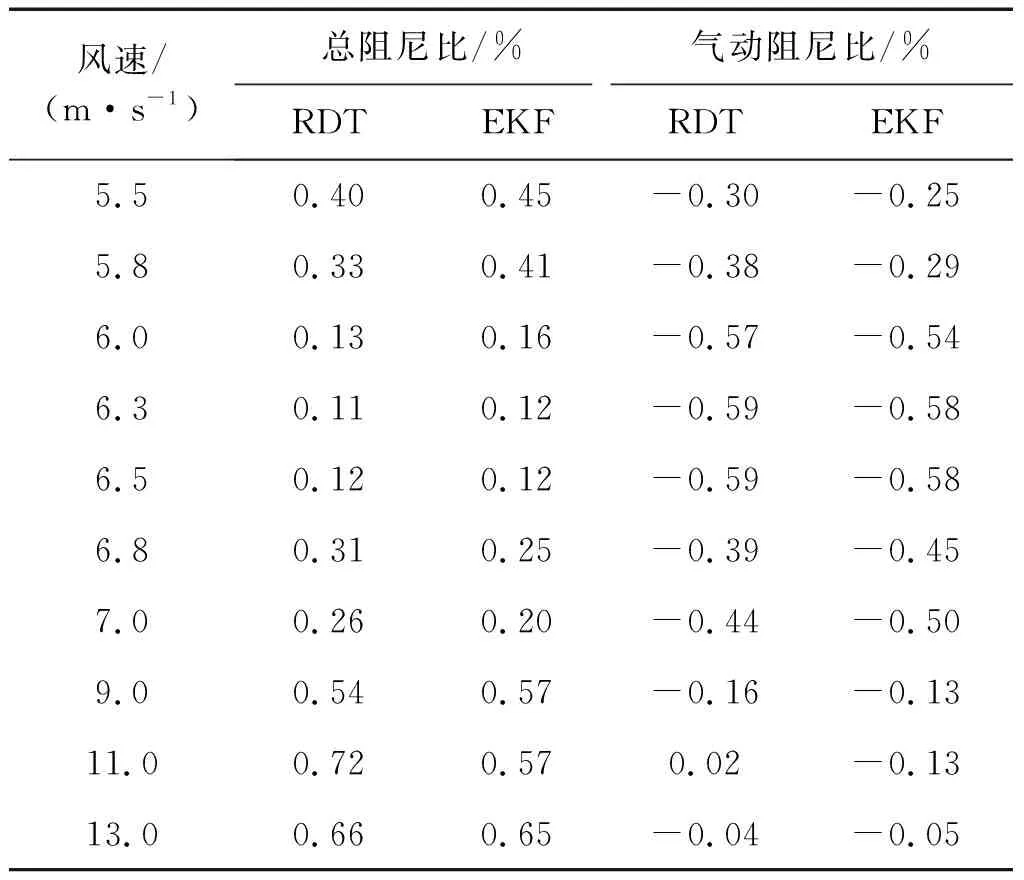
表3 阻尼识别结果Tab.3 Identification results of damping

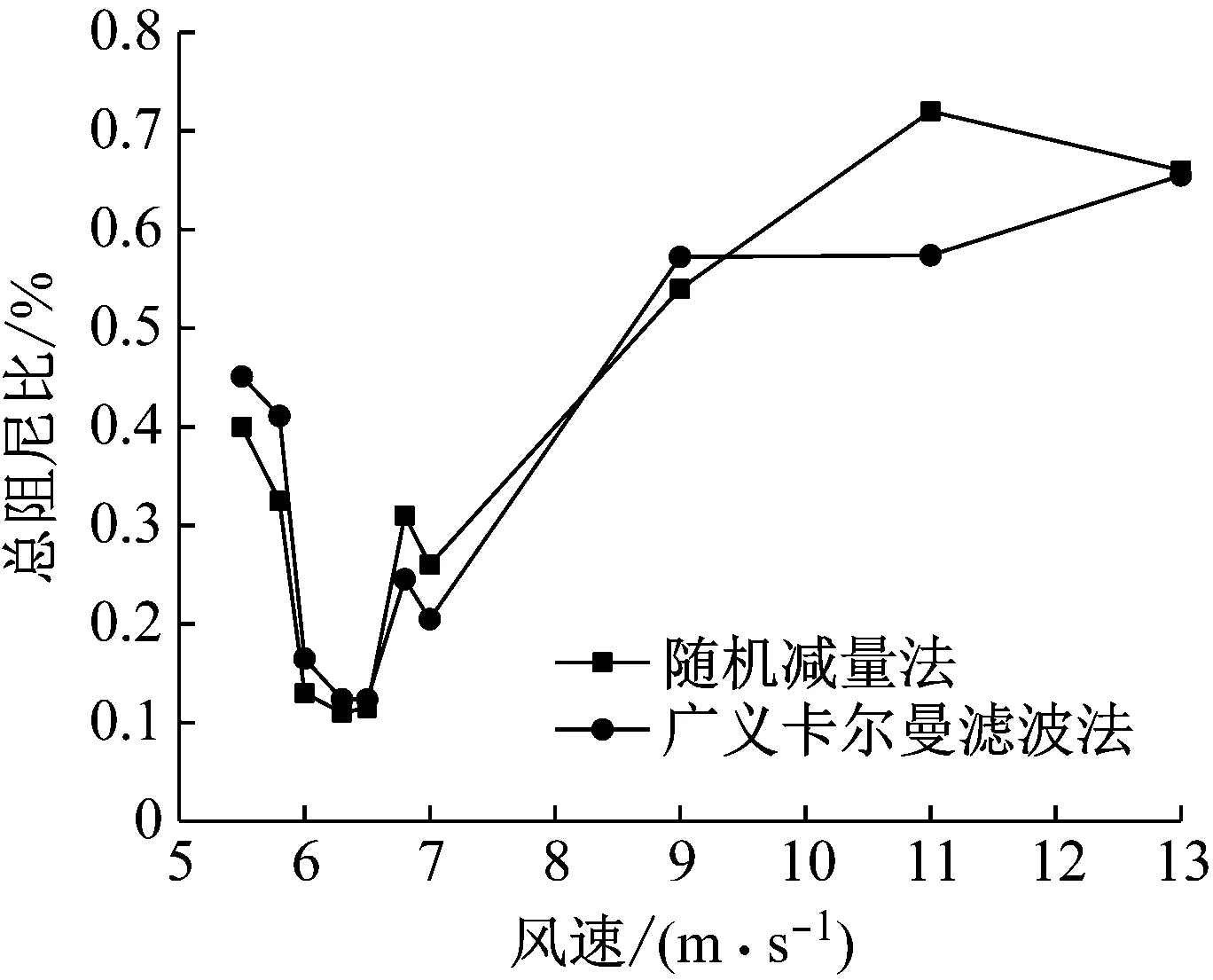
图15 总阻尼比识别结果Fig.15 Identification results of total damping ratios

图16 气动阻尼比识别结果Fig.16 Identification results of aerodynamic damping ratios

从图中可以看出当结构阻尼比增大时，横风向加速度响应可以得到抑制，尤其是在涡激共振区间的抑制效果更加明显。从阻尼角度出发，Noor III吸热塔已成功安装由陈政清团队研发的电涡流TMD对其进行减振，减振效果明显。

7 结 论

(1) 本文在已有的光热电站吸热塔气弹模型的基础上，进行了不同结构阻尼比下的风洞试验，获得了长持续时间(15 min)的模型顶部加速度时程，采用随机减量法和广义卡尔曼滤波法识别了不同结构阻尼比下的气动阻尼，两种方法的识别结果吻合较好，可以为吸热塔的设计和振动控制提供较好的参考依据。

(2) 从不同加速度幅值处识别的总阻尼比有如下规律：总阻尼比随着加速度幅值的增大先增大后减小。

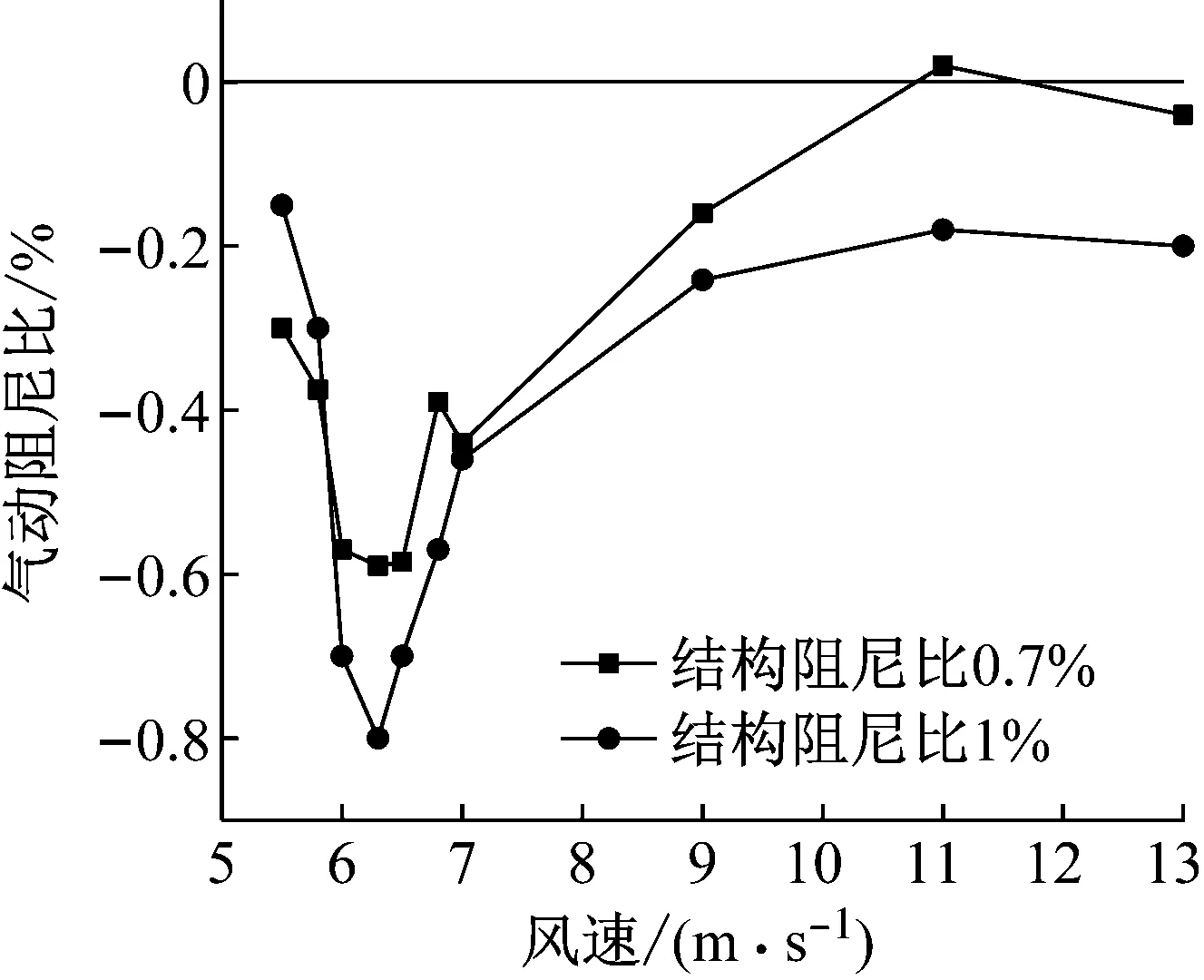
图17 不同结构阻尼比下的气动阻尼比识别结果Fig.17 Identification results of aerodynamic damping ratio under different structure damping ratios

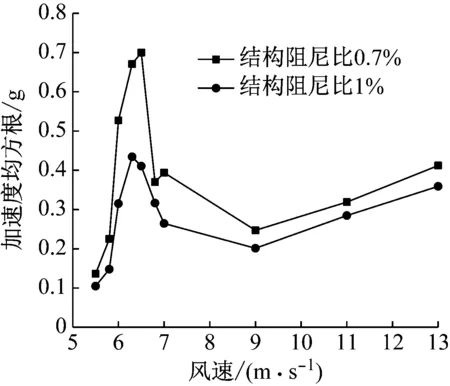
图18 不同结构阻尼比下的加速度均方根Fig.18 RMS of accelerations under different structure damping ratios

(3) 气动阻尼比的识别结果总体上有如下规律：随着风速的增大，气动阻尼比先减小后增大；风速6.5 m/s时的气动阻尼比为负的最小，此时的风速位于涡激共振区间内；涡激共振区间内气动阻尼比和加速度均方根均具有明显的峰值。这些规律可以为涡振区横风向响应起控制作用的现象提供合理的解释。

(4) 当增大结构阻尼比时气动阻尼比全部变为负值且有整体增大趋势，但不同结构阻尼比下识别的气动阻尼比随风速的变化规律是一致的。

(5) 本试验中结构阻尼比增加时，结构横风向响应得到抑制，对已有阻尼措施抑制涡振响应的结论进行了进一步验证。