基于VMD-HMM的滚动轴承磨损状态识别

李奕江， 张金萍， 李允公

(1.沈阳化工大学 机械工程学院，沈阳 110142；2.东北大学 机械工程与自动化学院，沈阳 110004)

滚动轴承是旋转机械的重要组成部分，在数控机床和机器人等运动精度要求较高的领域，其运行状况直接关系到设备的精度和可靠性。磨损是滚动轴承失效形式中较为常见的一种，随着轴承长时间的工作，摩擦导致轴承内部间隙增大，粗糙度增加，轴承的运转精度因而下降。在精密机械中所广泛应用的轴承经常是因为磨损失效而导致设备的运转精度降低。相关研究表明百分之三十的旋转机械故障是由轴承的失效引起的[1]。因此，对滚动轴承进行故障诊断和磨损状态监测的研究非常重要。

在滚动轴承磨损失效方面，大量学者进行了相关研究，文献[2]综述了声发射技术在滚动轴承磨损研究上的进展；文献[3]在预测轴承磨损寿命上使用了灰色系统理论，得到了较为精确的预测结果；文献[4]仿真验证了圆柱滚子轴承的不均匀磨损特性；然而上述文献对滚动轴承的磨损状态分类研究少有涉及，也没有找到可以分类的特征值。

隐马尔可夫模型具有强大的动态时间处理能力，可以对轴承的磨损状态进行识别与诊断[5]；在以往的轴承故障诊断研究中，其信号分解常常采用的方法有：小波变换，希尔伯特变换、经验模式分解(Empirical Mode Decomposition,EMD)、总体经验模式分解(Ensemble Empirical Mode Decomposition,EEMD)等。目前，文献[6]提出了基于二进制小波包变换的轴承故障诊断方法，能够准确过滤出故障瞬态冲击成分；文献[7]提出了基于EMD的无量纲索引方法，可以实现旋转机械的故障诊断；文献[8]提出一种基于EEMD的多变量多尺度统计过程监测方法，开发的方法能够有效地提取轴承故障特征，得到可靠的轴承故障检测和诊断策略。上述方法在轴承故障诊断上取得了良好的效果，但也存在着一些局限性，小波分析中的小波基难以选择，需要较平稳的信号且抑制脉冲干扰能力较低。EMD的算法效率低下，存在模式混叠现象，EEMD虽然抑制了模式混叠现象，但算法效率低的弊端依然存在。由于现场采集的轴承振动信号是非线性非平稳的，往往存在窄带脉冲干扰和随机信号，大量的干扰会掩盖轴承的故障特征信号，严重影响了轴承磨损状态的识别。

变分模态分解(Variational Mode Decomposition, VMD)是一种诞生于2014年的新的非递归、自适应的数据分解方法[9]，它是一种新的数据分解算法，分解层数少算法效率高，没有模态混叠和端点效应[10]，且分解后所得的各层IMF(Intrinsic Mode Function)中包含着丰富的故障信息。因此本文从滚动轴承不同磨损状态的振动信号入手，充分利用VMD分解对非平稳信号的处理能力和HMM(Hidden Markov Model)模型极好的模式识别功能，将VMD分解和能量熵与HMM模型结合起来，应用到滚动轴承的磨损状态识别中，最后通过实验验证了该方法的准确性与稳定性。

1 变分模态分解

变分模态分解在“变分”过程中使用二次惩罚因子α和拉格朗日惩罚算子λ(t)，使有约束变分转化为无约束变分，然后通过交替方向乘子法迭代搜寻变分模型最优解，来不断更新每个模式分量的带宽和频率中心，最终自适应的实现信号的有效分解。

1.1 VMD分解原理

VMD算法分解所得的本征模式分量(Local Mean Decomposition,IMF)与EMD和LMD分解的IMF不同，它被重新定义为一个调幅-调频信号，数学表达式为

uk(t)=Ak(t)cos[φk(t)]

(1)

式中：Ak(t)为uk(t)的瞬时幅值，且Ak(t)≥0;φk(t)为相位，它为非负函数，且φk(t)≥0；ωk(t)为uk(t)的瞬时频率。

(2)

式中:uk(t)可以认为是一个谐波信号，它的幅值为Ak(t)、频率为ωk(t)。

VMD算法分解信号x(t)后，得到K个离散的的模态uk(t)(k∈1,2,…,K)，它在频域中具有稀疏特性，通过以下方法估计各模态信号频率带宽：

(1)通过对模态函数uk(t)进行Hilbert变换，得到边际谱。

*uk(t)

(3)

(2)调整指数修正，将每个估计的uk(t)中心频带调制到相对应的基频带。

(4)

(3)计算解调信号梯度的平方L2范数。

(5)

在上述求解的基础上构造VMD变分约束模型，如式(5)所示

(6)

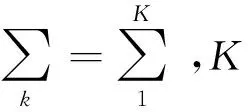
为了求解式(5)的变分约束模型的最优解，通过引入二次惩罚因子α和拉格朗日乘法算子λ(t)，即可将约束模型转化为式(6)所示的非约束模型问题，该增广拉格朗日函数如式(7)所示

L({uk},{ωk},λ)=

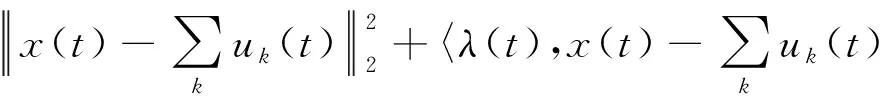
(7)

不断地使用ADMM法迭代搜索找到拉格朗日函数L的极小值点，原始信号x(t)被最终分解为K个模态函数uk(t)。

从以上VMD原理可以看出，VMD通过频域上的更新将傅里叶逆变化转换到时域上，相比于经验模态分解和局部均值分解，VMD具有更好的数学模型和理论且避免了模态混叠和端点效应，在机械振动信号和心电图信号的处理上有良好的效果。文献[11]将VMD分解的自适应形态学的特征提取方法并与粒子群算法相结合。通过仿真和试验分析，将其与EMD的自适应形态学、包络解调方法比较，结果表明VMD具有较高的精度，分解层数少效率高，克服了EMD的缺点，最终有效的提取了滚动轴承故障信号的特征频率。

2 HMM模型

隐马尔可夫模型(HMM)是一个概率模型，经常用来描述一个系统的隐性状态之间的转移和表现概率,已经在语音识别方面取得了显著的成果[12]。HMM是一个双重随机的过程，在该过程中隐状态必须满足马尔可夫性且隐状态能够大概被估计。隐马尔可夫模型中的每个状态不能被直接观测到但是可以通过观测值和随机过程进行间接的感知。每个观测值可以通过概率密度分布表现为它所对应的状态。由于其在时间序列上有着强大的分类处理能力，适合对滚动轴承的磨损状态演变进行分类。

一个离散隐马尔科夫模型一般由以下几个参数来表达:

(1)马尔可夫链隐状态数N。N个状态为S={S1,S2,…,SN}，t时刻的状态为qt,qt∈S。

(2)在各个隐状态下的可观测值数M。M个观测值为L={L2,L2,…,LM}，t时刻的观测值为Ot,Ot∈L。

(3)隐状态间状态转移概率矩阵

A={αij},αij=(qt+1=Sj|qt=Si),1≤i,j≤N

(4)观测值概率矩阵

B={βj(k)},βj(k)=P(Ot=Lk|qt=Sj),

1≤j≤N,1≤k≤M

(5)初始状态概率分布矢量

π={πi},πi=P(q1=Si),1≤i≤N

该离散HMM模型由N,M,A,B和π 5个参数表示，一般简记为λ=(π,A,B)。

3 VMD-HMM磨损状态识别过程

随着滚动轴承磨损状态的不断改变，轴承振动信号经VMD分解后的IMF分量也会有相应的改变。应用HMM在滚动轴承故障诊断中已经取得了一定的成果，而VMD分解在自适应性、正交性上有很大的优势且避免了EMD和LMD等的模态混叠和端点效应等缺点。因此本文提出了基于VMD-HMM的滚动轴承磨损状态识别算法，图1所示为利用VMD-HMM进行状态识别的主要步骤。

(1)随机选取滚动轴承磨合时期、正常使用、失效前期和失效期4种振动信号各20组共80组来作为训练信号，对每组信号进行VMD分解，根据能量熵定义计算每层IMF分量的能量熵参数，提取滚动轴承振动信号各层IMF分量能量熵构成能量熵序列共80组，然后将能量熵序列矢量量化后利用此序列输入到HMM模型中使用Baum-Welch算法进行训练，得到对应的各类磨损状态分类，形成磨损状态模型库。

(2)模式识别，对待诊断信号(剩余的80组)进行VMD分解并计算各层IMF能量熵，得到的能量熵序列矢量量化后，将此能量熵序列输入到已经训练好的4种磨损状态模型库中，HMM模型将会输出对数似然概率lnP(O∣λ)，所输出的最大的对数似然概率所对应的磨损状态即为该待诊断信号的磨损状态，从而实现轴承磨损状态的识别。

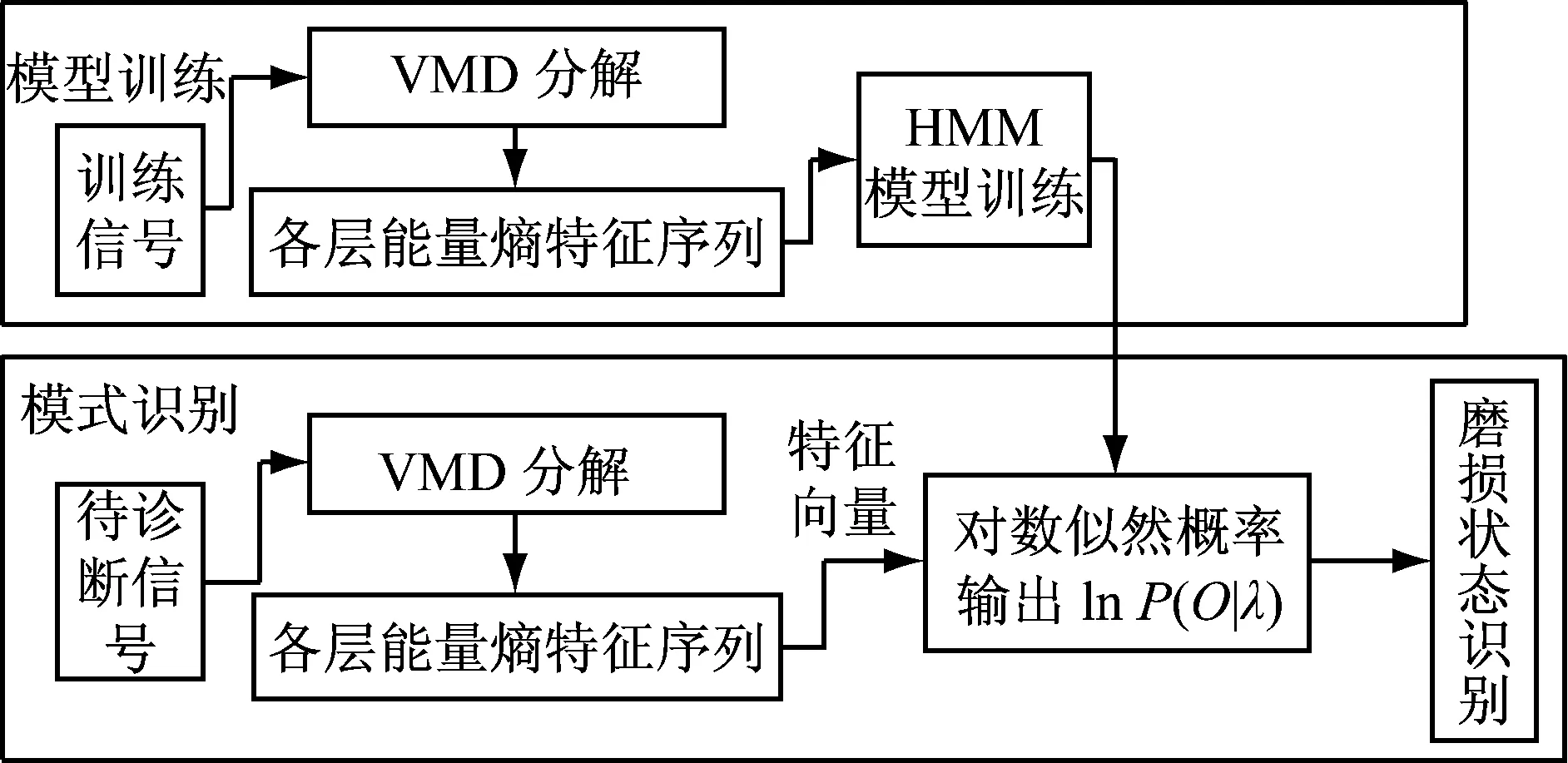
图1 VMD-HMM模型磨损状态识别过程Fig.1 Patter recognition procedure with VMD-HMM model

4 仿真实验

为了验证本文所使用的VMD算法的有效性，利用式(8)所示的仿真信号进行实验，并与EMD算法进行比较。

s(t)=x1(t)+x2(t)+x3(t)+n(t)

(8)

x1(t)=0.6sin(2π×10t)

(9)

x2(t)=0.4sin(2π×50t)

(10)

x3(t)=0.2sin(2π×100t)

(11)

式中：x1(t),x2(t),x3(t)为幅值和频率均不一样的正弦信号；n(t)为均值为0、方差为1的高斯白噪声。

设置仿真信号的采样频率fs=1 000，采样点数N=500，仿真信号的时域波形图如图2所示，然后分别对仿真信号进行EMD,VMD分解，分解后得到的结果如图3～图6所示。

图2 仿真信号时域波形Fig.2 Time-domain waveform of simulation signals

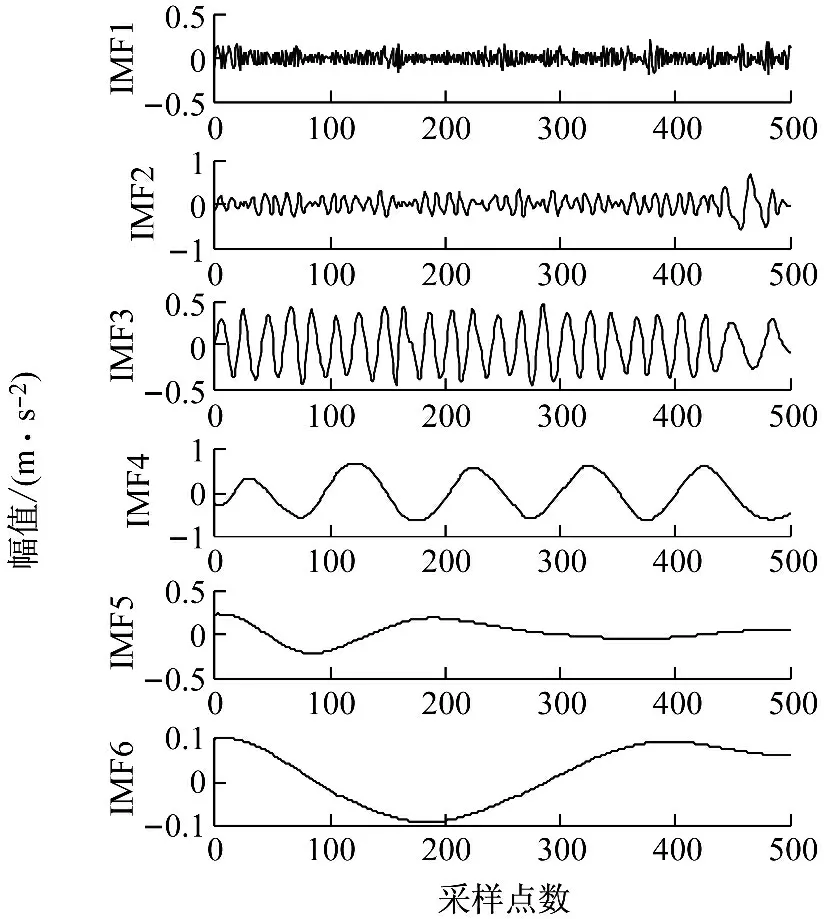
图3 仿真信号EMD分解结果Fig.3 The result of simulation signal after EMD

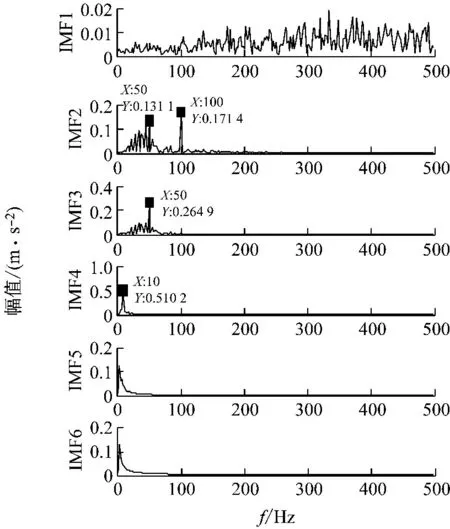
图4 EMD分解结果幅频图Fig.4 Amplitude spectrum of EMD decomposition results

图5 仿真信号VMD分解结果Fig.5 The result of the simulation signal after VMD

图6 VMD分解结果幅频图Fig.6 Amplitude spectrum of VMD decomposition results

由图3和图4可以看出，EMD分解后的信号波形不规则，局部出现失真；IMF2出现了50 Hz和100 Hz两种频率成分，出现了模式混叠；EMD分解需要较多的分解层数才能达到好的分解效果。与图5和图6进行对比，VMD分解后所有的正弦频率被完整分解出来，IMF1对应x1(t)、IMF2对应x2(t)、IMF3对应x3(t)、IMF4为噪声信号，且波形和幅值均与原信号一致；各IMF之间没有模态混叠现象；VMD所需的分解层数较少，且效果更好；VMD分解有更好的噪声鲁棒性。通过对比可以发现本文采用VMD进行信号分解可以有效提取出信号的特征频率且能抑制白噪声。

5 实验与分析

为了验证以上方法的有效性和准确性，进行了滚动轴承磨损状态全寿命周期实验。实验装置如图7所示，实测轴承来自某机械加工厂的一台线切割机床导轮轴承，信号采集与检测系统包括北京东方振动与噪声研究所得INV3018C智能信号处理分析仪、INV9822型ICP加速度传感器及DASP信号采集分析系统。

图7 实验测试情况Fig.7 Experimental test conditions

由于加工环境造成该线切割导轮轴承经常因磨损失效导致导轮精度降低，所以采集该线切割导轮轴承的全寿命周期振动信号，该轴承经过磨合，正常工作，性能退化直至磨损实效，最后对其进行更换处理。在导轮总成上安装传感器，从轴承开始更换时开始，每两天采集一次数据，持续60天采集了30组数据，采样频率19 682 Hz。

5.1 VMD分解与能量熵特征提取

根据轴承的性能，按时间顺序将其服役分为4个阶段：磨合阶段、正常阶段、早期磨损阶段、磨损失效阶段。磨合阶段的轴承刚开始使用，正常阶段的轴承可以正常使用，早期磨损阶段下的轴承有轻微的磨损，但是不影响使用，磨损失效阶段下轴承不能再继续使用，应进行更换。图8为测试轴承在正常状态和磨损失效状态下的时域振动波形图。将采集到的滚动轴承全寿命周期数据按轴承磨损状态分为4组，每种状态各分为40组数据共160组，对每组数据进行VMD分解，以轴承正常状态为例，选取最优分解层数为6层，惩罚因子α=500，其中一组正常状态的轴承数据分解结果如图9所示。图10为该组数据的EMD分解结果。

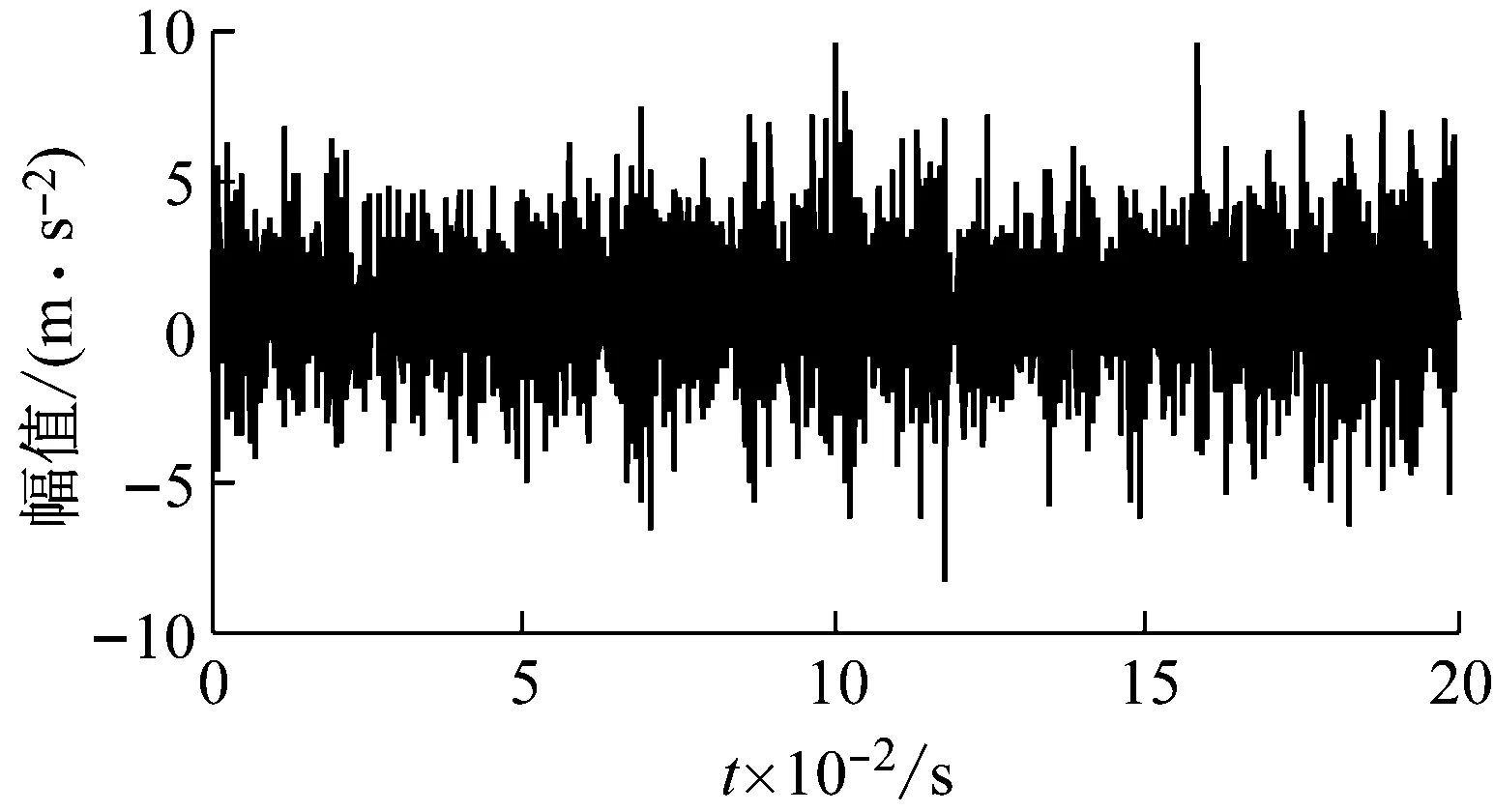
(a)正常状态

(b)磨损状态图8 实测信号Fig.8 Measured signal

从图10的分解结果可以看出IMF5,IMF6,IMF7三者之间存在模态混叠，同时EMD的分解层数较多，对接下来的数据处理会造成不便。反观图9的VMD分解结果，结果IMF1～IMF6由低频到高频排列，可以看出各IMF之间不存在模态混叠，且分解层数比EMD少，更便于后期处理数据。实验结果同时验证了VMD分解的优势。

然后将160组样本信号进行VMD分解，得到960组本征模态函数，根据能量熵的定义求取各组本征模态函数(IMF)的能量熵，IMF1～IMF6的特征参数为F1～F6，本文给出每种磨损状态各3组能量熵如表1所示。

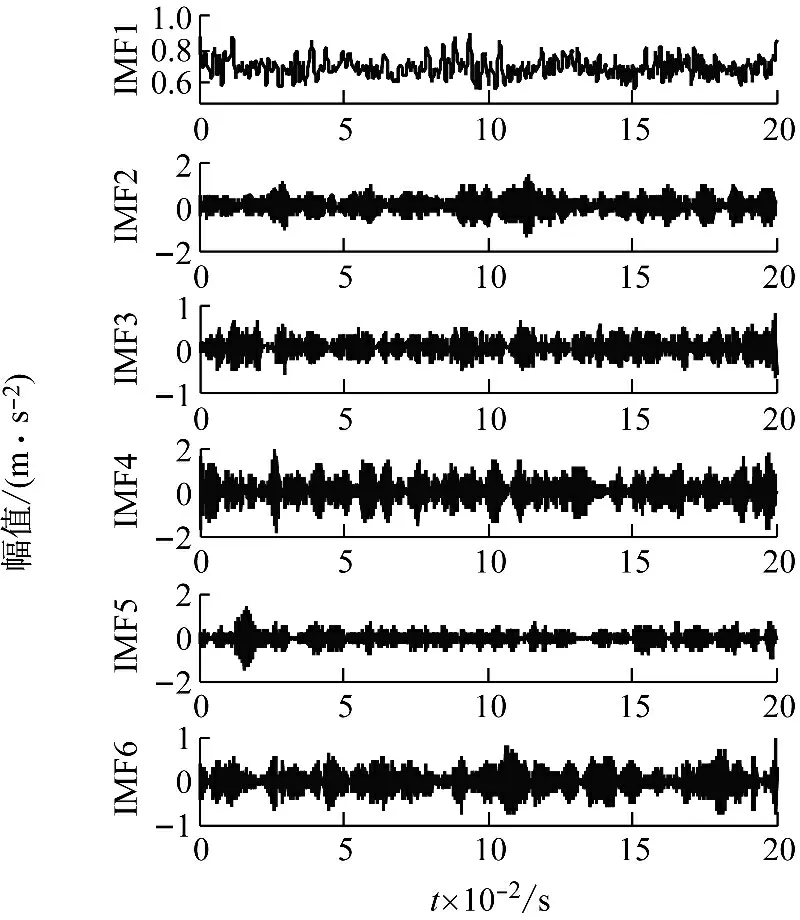
图9 正常状态轴承信号VMD分解结果Fig.9 Normal state bearing signal VMD decomposition result

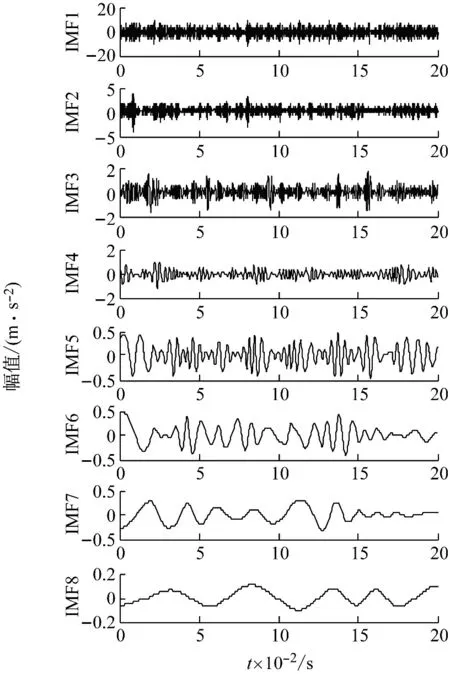
图10 正常状态轴承信号EMD分解结果Fig.10 Normal state bearing signal EMD decomposition result

5.2 HMM模型训练与磨损状态识别

HMM建模时采用VMD分解得到的6层IMF能量熵组成特征向量F={F1,F2,F3,F4,F5,F6}作为观测序列，初始概率π，初始状态转移矩阵A，初始观测值概率矩阵B均由随机函数取得，得到160×6特征矩阵。

在HMM的建模与训练时，把磨合状态、正常状态、早期磨损状态、磨损失效状态代表4种隐状态，记作λ1,λ2,λ3,λ4,HMM模型的观测序列为上述提取的6维能量熵特征序列；选择80组特征向量(每种状态20组)作为训练的样本，Baum-Welch算法训练HMM模型需要输入的特征为离散值，所以对每组特征向量进行矢量量化。HMM训练过程中，迭代次数增加最大似然估计也随之增加，最后模型达到收敛。训练结束后得到了4种状态所对应的HMM模型，图11给出了4种状态HMM的训练曲线。所有模型的迭代次数在30次时达到收敛，收敛较快。

表1 滚动轴承各磨损状态各层IMF能量熵Tab.1 IMF energy entropy of different wear state of roller bearings

经过上述训练后得到4种磨损状态HMM模型，将剩余的80组能量熵特征向量(每种状态20组)作为测试样本。测试前同样对特征向量进行矢量量化，将矢量量化后的能量熵序列分别输入到个状态的HMM模型中，每个模型都会输出一个对数似然概率lnp(O|λ)，这个对数似然概率表示观测值序列与所对应的HMM模型的相似程度，当该估计值越大时观测值与该HMM模型越相似，识别算法采用Viterbi算法，图12给出了每种测试样本在各HMM模型上的测试结果，通过对数似然概率可以准确识别出轴承当前所处的磨损状态。图12(a)中第10组数据分类错误，可能是因为该组磨合信号与正常信号有些相似。由图12(b)可知，正常状态的能量熵特征序列输入到该状态的HMM模型上时，其对数似然概率最大。从图12还可以看出，随着磨损状态的加剧4种状态的观测序列在同一模型上输出的对数似然概率也变大，滚动轴承4种磨损状态的识别成功率较高。实验结果表明VMD-HMM滚动轴承磨损状态识别模型可以成功的识别出滚动轴承的磨损状态，算法效率较高，识别准确率高，稳定性好。

图11 HMM训练曲线Fig.11 Curves of HMM training

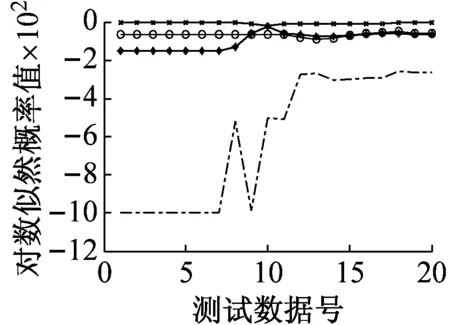
(a)磨合状态数据在各HMM模型上的输出值

为了比较验证该VMD-HMM模型的识别效果，采用EMD-HMM模型、谐波小波样本熵与HMM模型对相同的训练样本进行处理，最后进行识别结果的对比。EMD-HMM模型采用文献[13]介绍的方法，谐波小波样本熵与HMM模型结合的方法采用文献[14]中介绍的方法，最终得到的识别结果如表2所示。

由表2结果分析，在较少的样本情况下，EMD-HMM、谐波小波样本熵结合HMM和VMD-HMM对磨损状态的识别率分别为90%,95%和98.75%，EMD-HMM模型的各状态识别成功率在3种模型中最低，谐波小波样本熵结合HMM模型的识别成功率高于EMD-HMM模型，VMD-HMM模型的各状态识别成功率和综合识别成功率在3种模型中最高。这表明VMD-HMM模型可以有更好的识别率且其性能更为优越，可以有效的解决轴承磨损故障的分类问题。

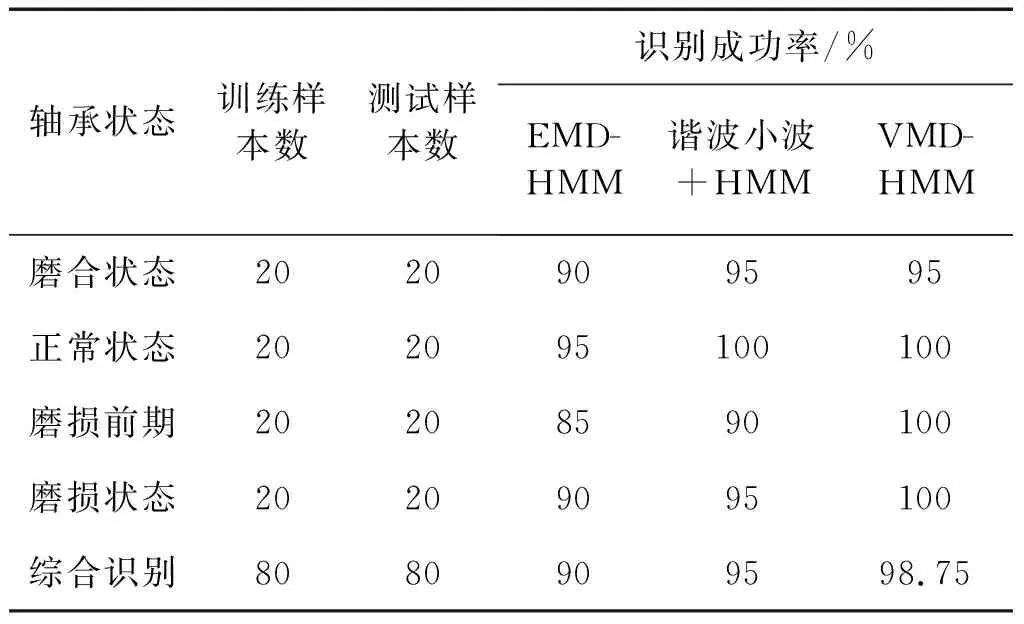
表2 3种模型识别正确率对比Tab.2 Recognition accuracy of three models

6 结 论

鉴于VMD分解和HMM的优点，本文提出了一种基于VMD分解和HMM模型的滚动轴承磨损状态识别方法。最后，为了验证所提出方法的可行性与有效性，实际记录了一位于易受磨损部位的的滚动轴承60天全寿命周期振动信号。将该组信号分为四类磨损状态，并训练了对应的4种HMM模型，最终用待测数据实现了滚动轴承磨损状态的识别，并与EMD-HMM模型和谐波小波样本熵结合HMM模型进行了对比。实验结果表明：

(1)VMD分解适合滚动轴承磨损的非平稳信号处理，具有很强的识别能力，分解出的各层本征模态函数没有模式混叠和端点效应，可以反映出各个频段的大致信息。

(2)基于VMD分解与能量熵结合，可以捕捉到不同磨损状态间所隐含的信息，从而可以有效的提取出轴承磨损状态的特征向量。

(3)HMM模型对轴承4种磨损状态进行训练，成功地对轴承磨损状态进行了识别，识别率较高，非常适合轴承磨损这种随时间变化，信号非平稳，特征重复性不佳的故障。