从联系的角度看三角恒等变换

朱胜强

学习三角恒等变换这一章时，让不少同学心生畏惧的可能要数众多的三角公式了.学习公式需要记住公式、理解公式，更要能够有效地应用公式解决问题，要实现这一目标，一个有效的办法是从联系的角度来看待三角恒等变换公式.

一、公式网络图

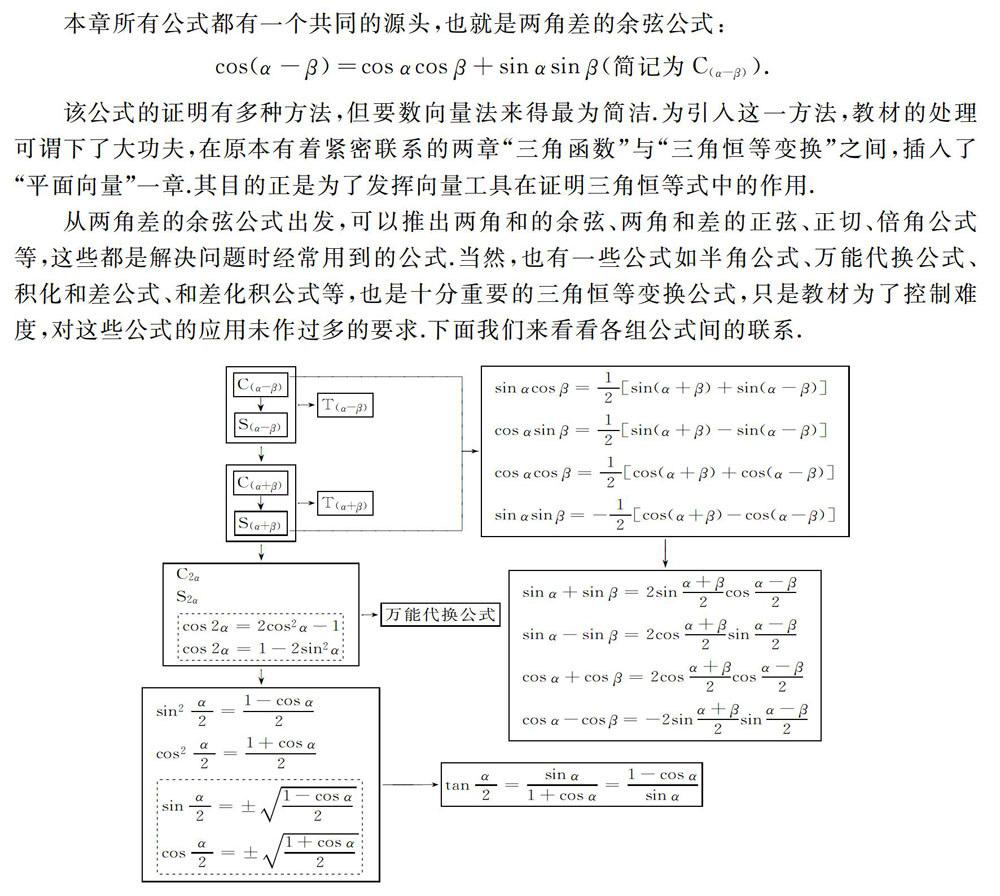
本章所有公式都有一个共同的源头，也就是两角差的余弦公式：

该公式的证明有多种方法，但要数向量法来得最为简洁，为引入这一方法，教材的处理可谓下了大功夫，在原本有着紧密联系的两章“三角函数”与“三角恒等变换”之间，插入了“平面向量”一章，其目的正是为了发挥向量工具在证明三角恒等式中的作用.

从两角差的余弦公式出发，可以推出两角和的余弦、两角和差的正弦、正切、倍角公式等，这些都是解决问题时经常用到的公式.当然，也有一些公式如半角公式、万能代换公式、积化和差公式、和差化积公式等，也是十分重要的三角恒等变换公式，只是教材为了控制难度，对这些公式的应用未作过多的要求，下面我们来看看各组公式间的联系.把握了公式间的联系，认清每个公式的来龙去脉，也就不用担心公式会忘了.

二、公式是建立联系的工具

说到三角恒等变换公式很容易想到繁琐的计算、人为技巧化的难题，这些当然不是学习这部分内容的重点所在，有了公式，便有了转化的途径，可以建立不同对象间的联系，

以函数为例.我们知道，函数是高中数学的主干知识，对高中数学内容起着统领作用.函数的学习并不因研究完几个具体函数而结束，还会在后续学习中不断深化，事实上，三角恒等式也为我们提供了建立函数间联系的机会.

三、从差异背后找联系

三角恒等变换公式——恒等，是指变化前后数量的本质保持不变；变换，则是指变化前后的形式的改变.发生改变，也就是形式上有了差異.在用公式时，这种差异往往是建立联系的出发点，是选用公式的依据.

一般说来，三角函数式恒等变形前后可能发生三种差异，一是角的差异；二是函数名的差异；三是运算形式的差异，角的差异则是其中最主要的差异，当角的差异消除了，所有三角函数都有同样的角，只要运用同角三角函数关系式便可以完成接下来的变化.当函数名的差异又消失了，消除最终的差异也就变得轻而易举了，

当函数名的差异清除了，运算形式也很自然地变得一致了.

当然，也可以从另一角度来思考，将x转化为2x.这可以使我们体会到，差异之间，是由公式为纽带联系着的，每个公式在消除差异方面都有各自的功能特点，将这一点认识清楚了，公式的运用也就变得得心应手，

公式就是建立联系的工具，学习公式，深入理解公式，灵活应用公式都离不开联系的观点.何止是三角恒等变换公式，其他公式不也同样如此吗？