基于无放回抽样的帕尔森窗口集成方法
何武超,王晓兰,何玉林,熊睿杰
1)沧州职业技术学院信息工程系,河北沧州 061001;2)深圳大学计算机与软件学院,广东深圳 518060;3)深圳大学大数据系统计算技术国家工程实验室,广东深圳 518060
帕尔森窗口(Parzen window)法[1]又称核密度估计方法[2],它利用多正态分布的叠加去拟合数据真实的概率分布,是一种建立在大样本理论之上的无参数概率密度函数估计方法,也是一种真正的从数据本身出发研究数据分布特征的方法[3].该方法在有监督学习[4]、无监督学习[5]、特征选择[6]和图像处理[7]等领域有广泛应用.
用帕尔森窗口法进行概率密度函数估计的关键在于窗口宽度(bandwidth)参数的确定[8],其中代表性的工作有SILVERMAN[9]的拇指原则(Silverman’s rule of thumb)、TERRELL[10]的过平滑窗口选取规则(over smoothed bandwidth selection rules)、ALEXANDRE[11]的solve-the-equation法、茹杨等[12-13]的迭代solve-the-equation法等.尽管帕尔森窗口法在实际应用中有着良好的概率密度函数估计表现,但仍存在显著缺陷:① 计算复杂度较高,不适合较大规模数据集的概率密度函数估计;② 对窗口宽度参数敏感,估计表现严重依赖于窗口宽度参数的确定.为解决上述问题,本研究基于无放回抽样的帕尔森窗口集成(sampling without replacement-based Parzen window ensemble,SR-PWE)机制,通过抽样和集成策略提高了传统帕尔森窗口法的效率和精度.
1 帕尔森窗口法
为简便起见,本研究仅讨论一维概率密度函数估计的情况.假设由随机变量X的N个观察值构成的数据集D={x1,x2, …,xN}, 其中xn∈R,n=1, 2, …,N, 对于大多数的实际应用而言,X的概率密度函数p(x)未知,经典的对p(x)进行估计的方法为帕尔森窗口法,即

(1)
其中,h为窗口宽度,h>0, 它是关于N的函数,取值满足式(2)的条件

(2)
由式(1)可见,帕尔森窗口法是用N个正态分布N(xn,h)的叠加去拟合未知的概率分布.这导致当N过大时,帕尔森窗口法需耗费较多的计算时间去处理大规模数据的概率密度估计问题.同时,帕尔森窗口法的估计表现严重依赖窗口宽度h的选取[8]:较小的h常导致较为粗糙的拟合,而较大的h又易导致较为平滑的拟合.对于h的选取尚无统一准则,至今仍是学界关注的难点和热点.
2 无放回抽样

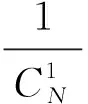
(3)

(4)
由式(4)可见,P1=P2.
3 SR-PWE方法
SR-PWE方法的实现过程为:
1) 对数据集D进行Q次无放回抽样,得到Q个D对应的抽样数据集
(5)


2)采用帕尔森窗口法估计抽样数据集的基概率密度函数
(6)
其中,窗口宽度为

(7)
3)采用求和平均的方式对基概率密度函数进行集成,从而估计数据集D的概率密度函数为

(8)
4 实验验证
为验证SR-PWE方法的可行性和有效性,比较并分析在柯西分布和正态分布上对比帕尔森窗口法和SR-PWE方法的概率密度函数估计表现.
4.1 实验数据和设置
表1给出了两种经典概率分布的详细信息.本研究采用如式(9)[18]的Matlab命令生成服从柯西分布(Cauchyrnd)和正态分布(normrnd)的随机数.

(9)
对于概率密度函数估计方法性能的评价,本研究采用如式(10)的均方根误差(root mean square error,RMSE)度量标准.
(10)
其中,p(xn)和p′(xn)分别表示数据xn对应的真实和估计概率密度值,n=1, 2, …,N.

表1 两种概率分布Table 1 Two probability distributions
4.2 实验结果与分析
为了验证子集个数Q和子集规模M对SR-PWE方法估计表现的影响,本研究分别对其在柯西分布和正态分布上的RMSE值进行了分析,并进一步与使用帕尔森窗口法的估计表现进行对比.该估计表现由其RMSE值体现,令Q={10, 20, …, 200}和M={25, 50, 75, 200}, 分别测试对于给定的Q, SR-PWE的估计表现随M的变化情况,以及对于给定的M, SR-PWE的估计表现随Q的变化情况.对于每种分布生成2×104个随机样本(结果从100次独立实验中随机选取的.实验源代码请扫描论文末页右下角二维码).图1展示了在柯西和正态两种概率分布上参数Q和M对SR-PWE概率密度函数估计表现的影响情况.
从图1可见,对于给定的子集规模M, 随着子集个数的增加,SR-PWE在两种概率分布上对应的RMSE值均逐渐减少,直到趋于收敛.同时,对于给定的子集个数,随着子集规模M的增加,SR-PWE对应的估计误差也是逐渐减小的.这表明我们设计的基于无放回抽样的帕尔森窗口集成方法是可行的.同时在图1中还可发现,SR-PWE的估计效果显著优于帕尔森窗口法在全部数据上的概率密度函数估计.表2给出了帕尔森窗口和SR-PWE在两种分布上具体的估计效果对比,通过总结SR-PWE的8个(Q,M)参数对对应的RMSE值,从中发现SR-PWE每个参数对对应的RMSE值均低于帕尔森窗口,证实了SR-PWE方法的有效性.

图1 两种概率分布上参数Q和M对SR-PWE估计表现的影响Fig.1 (Color online) The impacts of Q and M on the estimation performance of SR-PWE based on Caudy and normal probability distributions

表2 SR-PWE的估计表现1)Table 2 The estimation performance of SR-PWE
1)·表示均方根误差小于帕尔森窗口法
结 语
针对传统帕尔森窗口法计算复杂度高、对窗口宽度参数敏感的缺陷,本研究设计了一种基于无放回抽样的帕尔森窗口集成方法,该方法具备处理大规模数据集概率密度函数的能力,通过将大数据集切分成与大数据集保持概率分布一致性的数据子集,可将数据子集上估计的基概率密度函数集成得到原始数据集的概率密度函数.实验结果表明,该方法的概率密度函数估计效果显著优于经典的帕尔森窗口法,证实该方法可行且有效.

