基于ARIMA-Kalman滤波器数据挖掘模型的油井产量预测

谷建伟，隋顾磊，李志涛，刘 巍，王依科，张以根，崔文富

1)中国石油大学(华东)石油工程学院，山东青岛 266580；2)中国石化胜利油田分公司勘探开发研究院，山东东营 257015；3)中国石化胜利油田分公司胜利采油厂，山东东营 257015

油田产量是反映油田开发效果的重要指标，是掌握油田动态变化的重要依据．在不同的开发阶段，影响产量变化的因素不同，但始终遵从地下渗流规律，且这些影响因素之间存在各种关联．目前，描述油田产量变化的方法有2种：一是基于基本的渗流理论油藏工程类方法[1]，如产量递减分析[2]．该方法是预测和分析油藏动态的常用数理统计方法，也是油藏工程类的典型代表之一，适用于产量递减阶段的油田．由于石油生产不断受到各种技术的干预，如采取压裂和酸化等增产增注措施的油气井，产量递减分析具有一定的局限性．油藏工程类方法考虑了储层性质、井况和生产控制参数对产油量造成的影响，但由于目前的渗流理论是在理想渗流环境下得到的，不能完全反应实际油田渗流的现象和规律[3]．二是基于数据挖掘的机器学习类方法[4-6]．EDIGER[7]采用差分自回归积分移动平均(autoregressive integrated moving average, ARIMA)模型预测土耳其石油产量，证明ARIMA回归和置信区间的吻合度越高越能提高产量预测模型的精度和可靠性．王滨等[8]应用时间序列传递函数模型建立了考虑因素动态关系的多因素油田产油量数据拟合模型，但并未用于产油量预测．FRAUSTO-SOLS等[9]通过应用ARIMA、NARX神经网络、单指数平滑以及双指数平滑等模型预测石油产量，证明了ARIMA模型预测精度良好．但是，ARIMA模型虽然具有高效的时序影响分析能力，却有一定滞后性[9]．

本研究以单口生产井的产油量为时间序列，根据该油井的历史产油量数据建立时间序列中的产油量ARIMA模型，并结合卡尔曼滤波器(Kalman filter)[10]，构建基于ARIMA-Kalman滤波器[11]的产量预测模型．ARIMA-Kalman滤波器具有高效的时序影响因素的分析能力，能够排除非同步性以及滞后性的影响，使识别出的产油量时间序列模型具有精准的拟合结果和预测能力，并缩短了滞后时间．

1 ARIMA-Kalman滤波器模型原理

ARIMA模型是将非平稳时间序列转化为平稳时间序列，然后将因变量仅对其滞后值及随机误差项的现值和滞后值进行回归所建立的模型[12]．在如式(1)的差分自回归移动平均模型ARIMA(p,d,q)中，p为自回归(auto regressive, AR)多项式的阶数，q为移动平均(moving average, MA)多项式的阶数，d为时间序列成为平稳时所做的差分次数．ARIMA模型根据原序列是否平稳以及回归中所含部分的不同，包括移动平均过程、自回归过程、自回归移动平均过程以及ARIMA过程[12]．如果研究的时间序列Qt是非平稳的，则可在标准的ARIMA模型中通过适当的差分获得平稳的时间序列．

(1)

其中，φ(B)为AR多项式；θ(B)为MA多项式；t为时间序列下标，t=1, 2, …；d为差分次数；e(t)为正常的白噪声序列，均值为0，方差为δ2；φi(t)为AR参数，i=1, 2, …；θj(t)为MA参数，j=1, 2, …．

平稳的时间序列用于建立ARIMA模型并确定其参数．参数(p,q)通过自相关函数(auto correlation function, ACF)和偏自相关函数(partial autocorrelation function, PACF)预先确定，根据AIC信息准则(Akaike information criterion)[13]最终确定．在时间序列分析中，Yule-Walker方程在模式识别和参数估计中起着重要作用[14]．ARIMA模型的残差可以作为模型估计准则，模型估计过程采用最大似然估计．通过求解残差序列的ACF，可以判断残差序列是否为白噪声．如果残差序列不是白噪声，则重新定义(p,q)．

因此，t+1时刻预测的产油量可描述为

Q(t+1)=φ1(t)Q(t)+φ2(t)Q(t-1) +…+

φp(t)Q(t-p+1)+e(t+1)-

θ1(t)e(t)-θ2(t)e(t-1)-…-

θq(t)e(t-q+1)

(2)

其中，Q(t+1),Q(t),Q(t-1), …,Q(t-p+1)为产油量时间序列；e(t+1),e(t),e(t-1), …,e(t-q+1)为残差时间序列．

ARIMA模型将预测对象随时间推移而形成的数据序列视为一个随机序列，用数学模型来近似描述该序列．此模型一旦被识别，就可以从时间序列的过去值以及现在值来预测未来值．

Kalman滤波器属于时变线性系统的递归滤波器，通过递归算法获取变量的最佳估计值，是将过去的测量估计误差合并到新的测量误差中来估计将来的误差．Kalman滤波器预测算法由状态方程(3)以及观测方程(4)组成．

Xt+1=AXt+Wt

(3)

Yt+1=BXt+Vt

(4)

其中，Xt+1为状态矢量；Yt+1为观测矢量；A为状态矩阵；B为观测矩阵；Wt和Vt为对应的白噪声矢量矩阵．

确定状态方程和预测方程的过程十分复杂，本研究拟将ARIMA模型的数学表达式引入到Kalman滤波器的状态方程和测量方程中，以期预测产油量状态．

令Q1(t)=Q(t),Q2(t)=Q(t-1), …,Qp(t)=Q(t-p+1);e1(t)=e(t),e2(t)=e1(t-1), …,eq(t)=eq-1(t-1)， 并将产油量数据ARIMA模型引入到Kalman滤波器预测算法的状态方程和测量方程中，则ARIMA模型可描述为

Q1(t+1)=φ1(t)Q1(t)+φ2(t)Q2(t) +…+

φp(t)Qp(t)+e1(t+1)-

θ1(t)e1(t)-θ2(t)e2(t)-…-

θq(t)eq(t)

(5)

由式(5)得出，Q2(t+1)=Q1(t),Q3(t+1)=Q2(t), …,Qp+1(t+1)=Qp(t);e2(t+1)=e1(t),e3(t+1)=e2(t), …,eq+1(t+1)=eq(t)． 因而可得ARIMA-Kalman滤波器预测算法的状态方程为

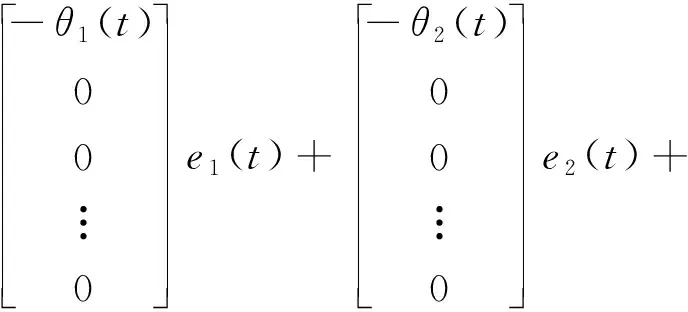
(6)

根据式(2)至式(6)，可得ARIMA-Kalman滤波器预测算法的观测方程为

Y(t+1)= [1, 0, …, 0]×

[Q1(t+1),Q2(t+1), …,

Qp(t+1)]T

(7)

由式(7)可见，ARIMA-Kalman滤波器预测算法基于历史产油量数据构建ARIMA模型，将ARIMA模型引入到Kalman滤波器中构建状态和测量方程，完成对噪声的滤波过程，最后根据确定的最优模型进行向后预测．图1是该预测算法实现的流程图．

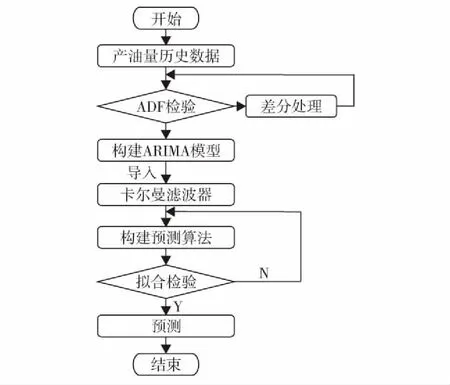
图1 ARIMA-Kalman滤波器预测算法流程图Fig.1 Predictive algorithm flowchart of ARIMA-Kalman filter

2 试验处理

2.1 平稳性处理

载入目标油井1991年1月—2016年9月月产油量时间序列数据，并绘制产油量时间序列曲线，结果如图2． 通过观察该数据序列图无法确定产油量时间序列是否稳定，需要对产油量时间序列进行平稳性检验，同时采用确定性时序分析方法提取产油量时间序列中所蕴涵的确定性信息．

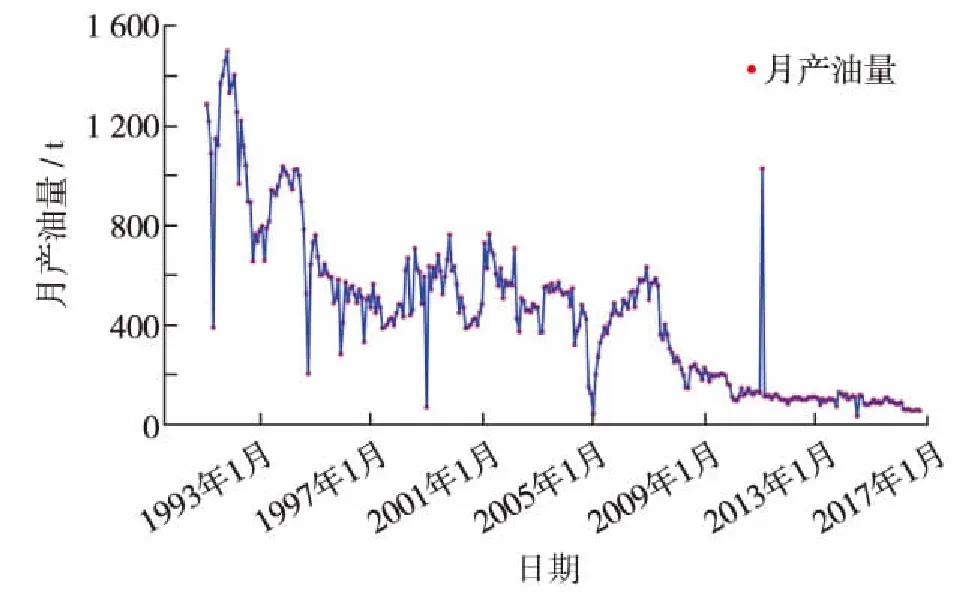
图2 月产油量时间序列图Fig.2 Oil production time series curve

ADF检验(augmented Dickey-fuller test)[15]假设序列至少存在1个单位根，即非平稳，对于一个平稳的时序数据，需在给定的置信水平上(通常置信区间取95%)显著，拒绝原假设．本研究为直观地分析产油量时间序列，采用对数变换(以自然对数为底)减小数据的振动幅度，消除异方差问题．经过对数变换的产油量时间序列曲线为图3中原始曲线，ADF检验结果如表1．由表1可知，ADF=-0.799 304，高于1%显著水平，P=0.819 326， 远大于0.05，接受原假设，说明产油量序列是一个非平稳序列．

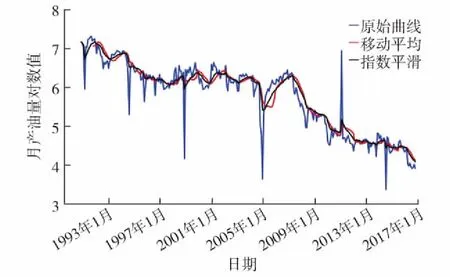
图3 产油量时间序列平滑曲线Fig.3 Oil production time series smooth curve

运用ARIMA模型进行时间序列分析需要将非平稳时间序列转化为平稳时间序列．为获得平稳的产油量时间序列，本研究采用式(8)移动平均和式(9)指数平滑两种确定性信息提取方法，其中n=12． 对对数变换的产油量序列进行移动平均和指数平滑结果如图3．

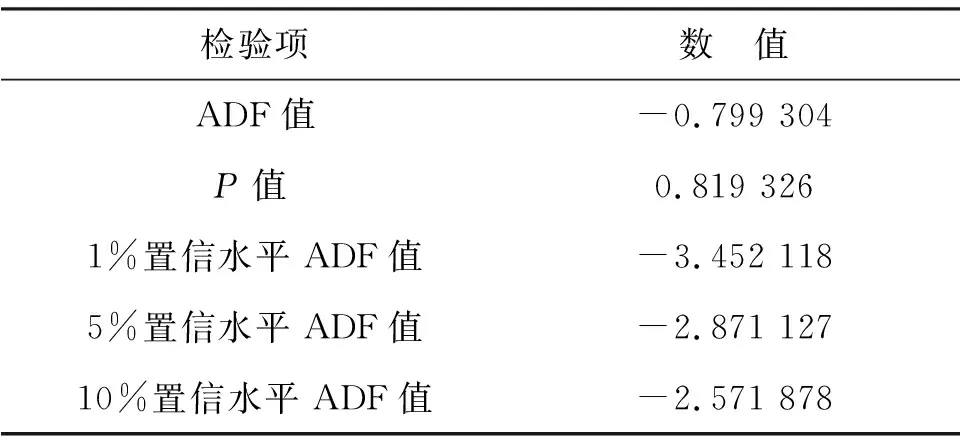
表1 产油量时间序列ADF检验结果Table 1 Oil production time series ADF test results

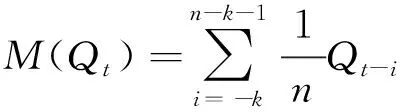
(8)

Qt=αQt-1+α(1-α)Qt-2+

α(1-α)2Qt-3+…

(9)

其中，α为平滑系数，本研究取α=2/(n+1)．

然而，移动平均和指数平滑对确定性信息提取都不够充分，BOX和JENKINS使用大量案例分析证明了差分处理是一种有效的确定性信息处理方法[16]，Cramer分解定理，如式(10)，则在理论上保证了适当阶数的拆分可以充分提取确定性信息．

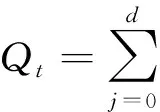
(10)

其中，β1,β2, …,βd为常数系数；at为一个零均值白噪声序列；Ψ(B)为随机性参数，B为延迟算子．

在Cramer分解定理保证下，式(11)的d阶差分就可以将{Qt}中蕴含的确定性信息提取出来．

(11)

其中， c为常数． d=1时展开得出1阶差分公式为

(12)

一阶差分后通过ADF检验确定序列的平稳性，结果如表2．由表2可见，ADF=-11.883 13，显著低于1%显著水平，P值远小于0.05，拒绝原假设，差分处理后的序列是一个平稳序列，即d=1．

表2 差分后产油量时间序列ADF检验结果Table 2 Differential oil production time series ADF test results

由图3可见，产油量时间序列具有明显的长期趋势，同时产油量时间序列也存在周期性的可能．依据相加分解模型和相乘分解模型理论分解产油量时间序列，可获得其长期趋势、周期性趋势以及残差曲线(图4)．由图4可见，产油量周期成分区间波动幅度小，可忽视周期性因素的影响．ARIMA差分模型白噪声检测P=4.844 24×10-13， 显著小于0.05，属于一个白噪声序列．因此，建模过程不需要考虑周期性组件以及重新定义(p,q)．

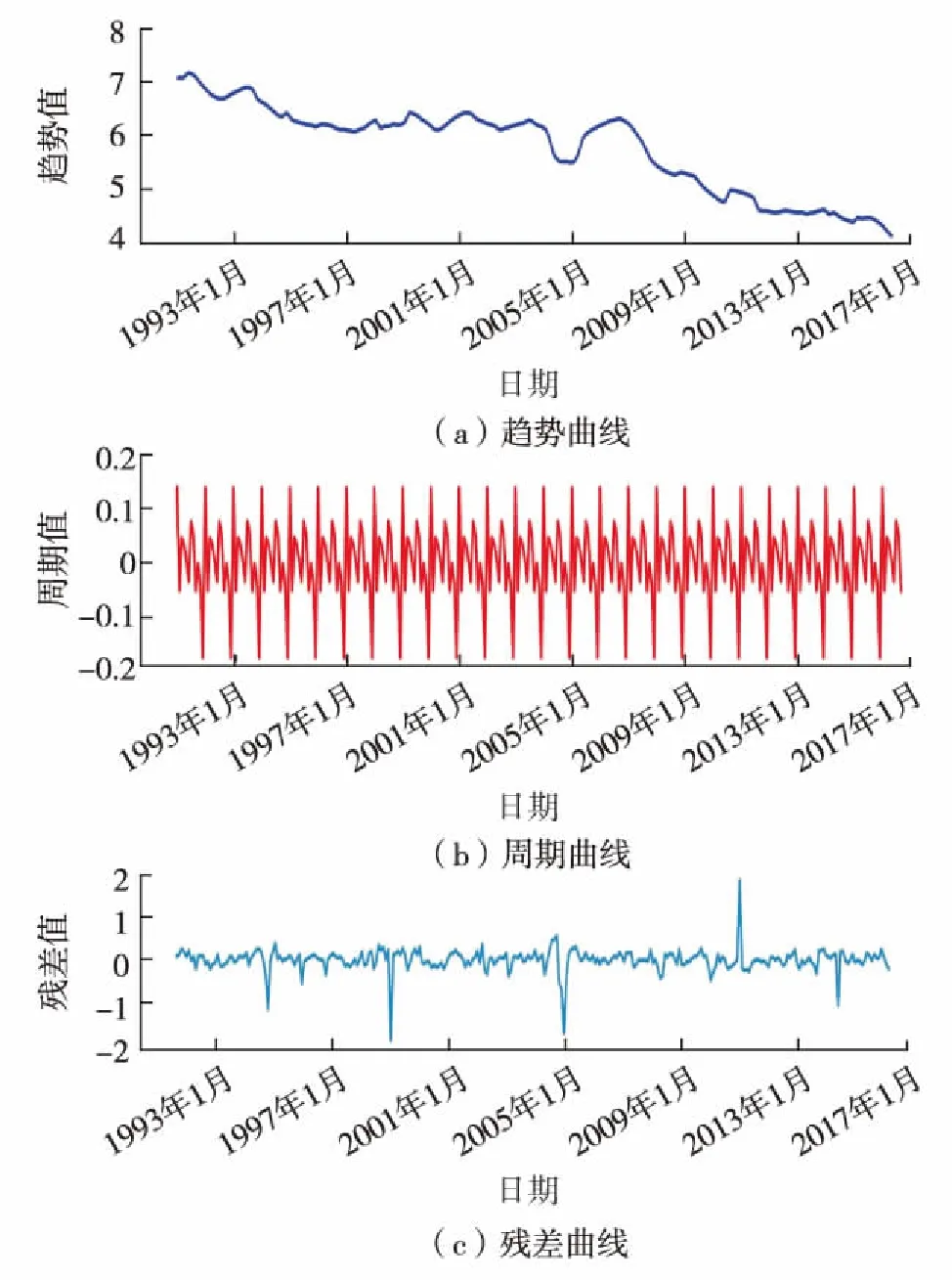
图4 分解后曲线成分Fig.4 Decomposed curve components

2.2 模型识别

产油量时间序列进行平稳性处理确定了差分项d， 随后分析ACF函数以及PACF函数，并确定参数(p,q)[17]． ACF函数是指有序的随机变量序列与其自身相比较反映了同一序列在不同时序的取值的相关性．PACF函数是指在剔除中间k-1个随机变量的干扰后，Qt-k对Qt影响的相关度量．统计分析对数变换后的产油量时间序列，获得ACF函数(图5)以及PACF函数(图6)．根据ACF图中曲线第1次穿过置信区间时获取q=1， 又根据PACF图中曲线第1次穿过置信区间时获取p=1.

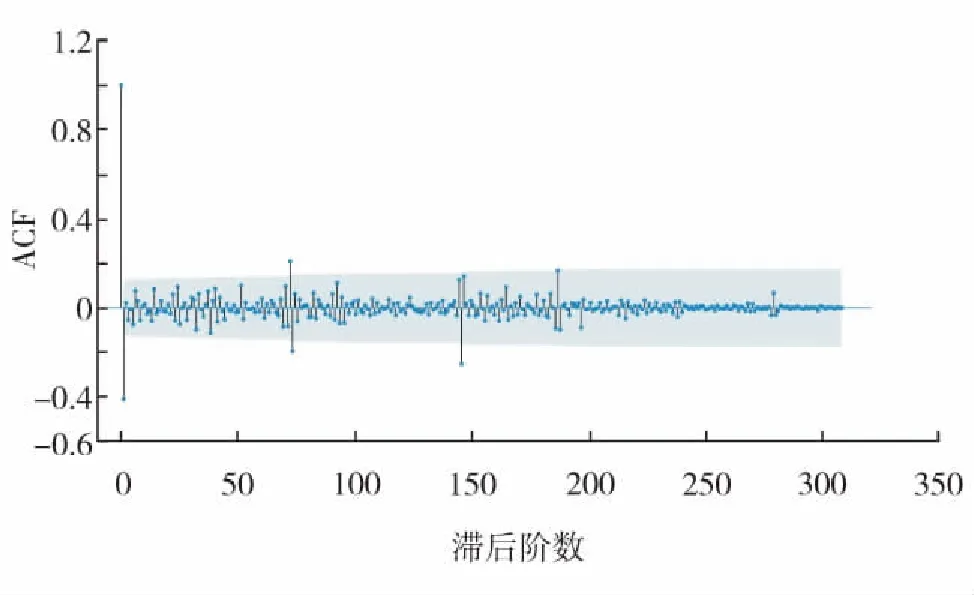
图5 ACF函数图Fig.5 ACF function diagram

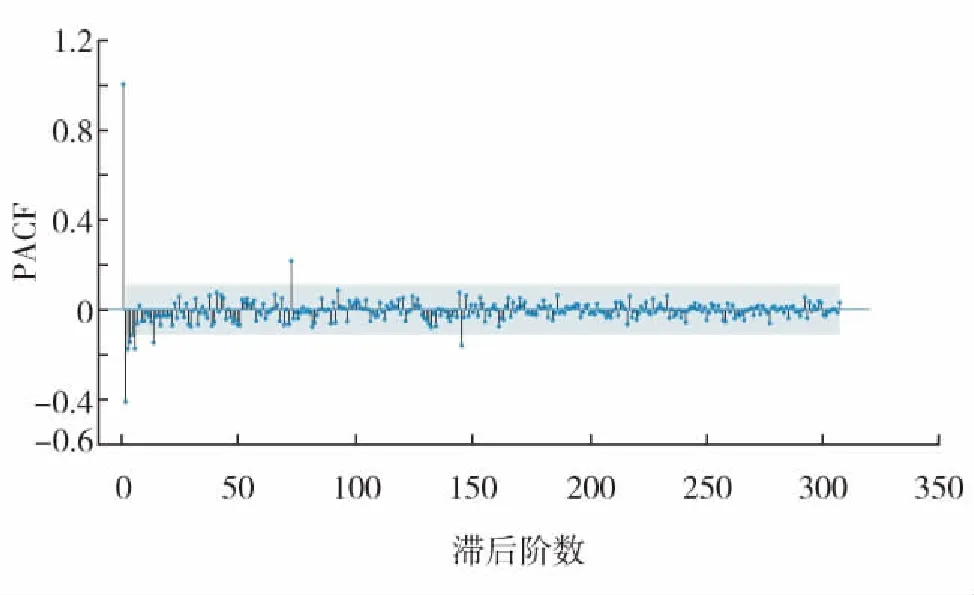
图6 PACF函数图Fig.6 PACF function diagram

依据AIC准则确定模型(1, 1)是否为最优的滞后因子阶数，鼓励数据拟合的优良性，但尽量避免出现过度拟合的情况．所以，优先考虑的模型应是AIC值最小的那一个．AIC准则的方法是寻找可以最好地解释数据，但包含最少自由参数的模型．表3给出不同(p,d,q)情况下的AIC统计值，从表3可见，(1, 1, 2)为最优模型．

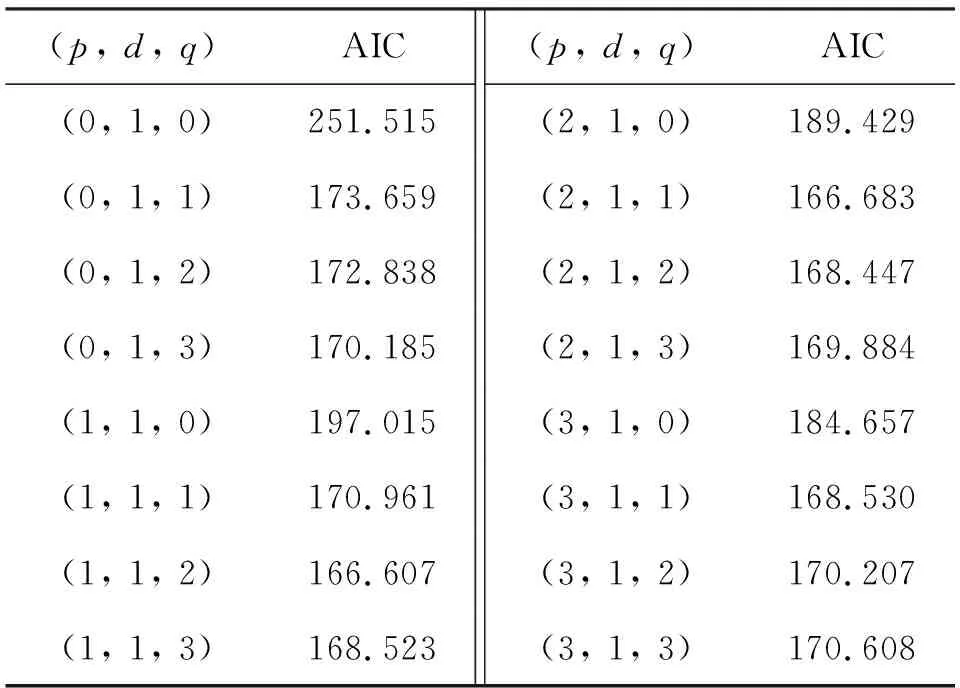
表3 AIC统计结果Table 3 AIC statistics results

确定产油量时间序列ARIMA模型结构识别为(1, 1, 2)，检验ARIMA(1, 1, 2)模型获取自回归以及移动平均参数，则该模型描述为

Q(t+1)= -0.009 6Q(t)+0.776 7Q(t-1)+

e(t+1)-1.352 5e(t)+

0.384 4e(t-1)

(13)

式(13)的ARIMA模型引入Kalman滤波器预测算法后，得出产油量时间序列ARIMA-Kalman滤波器模型为

(14)

2.3 数据拟合

根据产油量时间序列ARIMA-Kalman滤波器模型还原数据拟合效果，依据标准化的过程，将预测的产油量逆向还原，并根据历史上的实际月产油量，与实际值进行对比检验．从图7模型拟合结果可见，实际值与拟合值的吻合程度较高．

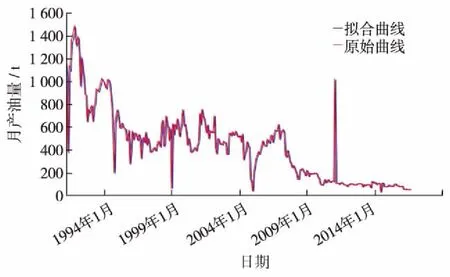
图7 产油量时间序列拟合结果Fig.7 Oil production time series fitting results

2.4 预 测

采用确定的ARIMA-Kalman滤波器模型预测2016年10月—2017年9月的单井实验区的产油量，并与该时间段的实际产油量进行对比(构造ARIMA-Kalman滤波器模型未载入2016年10月—2017年9月实际产油量数据)，结果如表4．由表4可见，此时间段内单井实验区的实际产油量为650.00 t，采用ARIMA-Kalman滤波器的预测产量为658.83 t，残差为8.83 t，相对误差为1.36%．

3 试验结果分析

产油量时间序列的影响因素十分复杂，一个微小的相关因素也可能引起产油量曲线发生急剧变化，同时各个因素之间存在一定的时序影响关系．同时，各种原因导致的结果需要一定的时间过程方能显现，因此预测的产油量时间序列具有非同步性和滞后性．

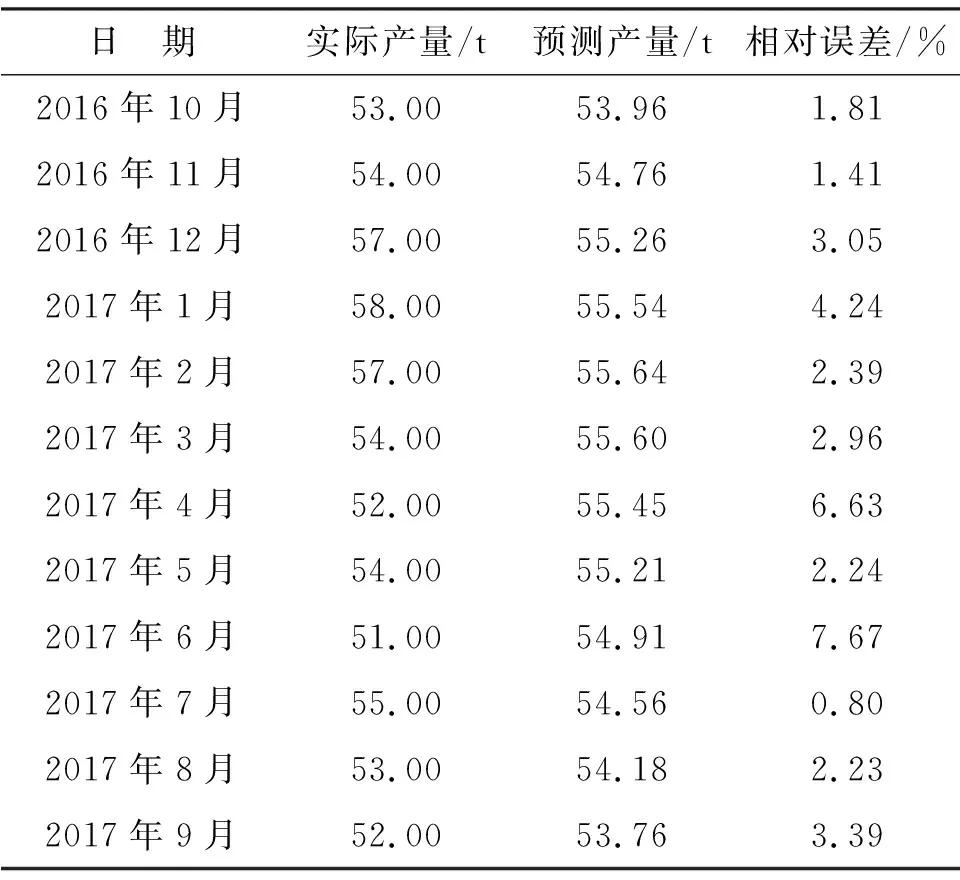
表4 2016年10月—2017年9月产油量实际值与预测值Table 4 Actual and forecasted oil production from October 2016 to September 2017

观察产油量时间序列，产油量曲线整体呈现长期递减趋势，主要是因为经过长期开采该区块储层剩余油储量逐渐减少．同时，为了减少层间干扰，工程人员采取分层注水技术提高注水波及系数，随后逐步采取了水力压裂、酸化等增产措施，因而2016年11月—2017年2月的产油量又有了显著回升．对比预测产量与实际产量，实际产量在2017年1月到达峰值，预测产量在2017年2月达到峰值，具有微小的滞后性，然而， EDIGER的研究模型[7]非同步性与滞后性显著．总体来说，产油量整体呈现长期递减趋势，局部呈现时升时降趋势，同时不能忽略个别月份油井产油时间较少等因素的影响．

4 结 论

1)建立了具有高效的时序影响因素的分析能力ARIMA-Kalman滤波器模型，该模型能够排除非同步性以及滞后性的影响，使识别出的产油量时间序列模型具有精准的拟合结果和预测能力．

2)运用ARIMA-Kalman滤波器模型进行区块产油量效果预测，2016年10月—2017年9月实际产量650.00 t，预测产量658.83 t，残差8.83 t，相对误差为1.36%，预测结果精度较高．

3)ARIMA-Kalman滤波器模型对油田产量预测是一种有效的尝试，该方法可为国内外油田产量及油田开发过程中含水率、产液量等宏观预测提供一种思路，为油田开发提供决策与理论依据．