一种基于结构特征的树相似度计算方法
陈彦桦,李 剑
(北京邮电大学 计算机学院,北京 100876)
0 概述
随着计算机技术和Internet的迅速普及,人们正在进入一个信息爆炸时代。伴随着海量数据急剧增加,迅速产生和积累了大量的结构化与半结构化数据,而对于这些数据,图挖掘算法的研究逐渐兴起并得到重视。树作为图的特殊表达形式,也有较为重要的研究意义。
在计算树的相似度方面,现已出现较多的研究。自文献[1]提出编辑距离算法后,研究者不断地对该算法进行改进。文献[2]提出基于树编辑距离的层次聚类算法,将树的编辑距离定义为d(T,T’)=min{r(P)|P是将T转化为T’的一系列树编辑操作},这些编辑操作包括插入、删除、转换节点。计算树的编辑距离就是求使T转化为T’所需树编辑操作的最少次数。因此,可以利用树的编辑距离计算树的相似度。每次计算时间复杂度为p×q×l2×l'2(树T、T’的长度分别为p、q,最大深度分别为l、l’),这是一个多项式的时间复杂度。
近年来,关于树的编辑距离有不少拓展的研究。文献[3]分析了基于无序树编辑距离的结构敏感变化问题。文献[4]提出了RTED算法,即一种鲁棒性的树编辑距离算法,解决了有序标记树的编辑距离问题。文献[5]展示了最大协议子树(MAST)问题和树编辑距离之间的关系。文献[6]对原本处理字符串编辑距离的GESL算法进行了扩展,将其应用到树的编辑距离中,在树的相似度计算上发挥了巨大的作用。文献[7]主要处理有序标记树的XML文档。该文指出常规的树编辑距离缺乏灵活性和效率,并提出了2个新的编辑操作,对原算法做了扩展,在与分层数据结构的相似性匹配上达到了良好的性能。文献[8]指出被广泛应用的RTED算法消耗内存过多,提出了一种新的树编辑距离算法AP-TED,该算法在时间性能上和RTED相当,并大幅减小了内存的使用。文献[9]主要研究无序的、有唯一标记的树。该文将编辑距离的原子操作定义为“局部移动”,并提出了一种新的树编辑距离算法SuMoTED,这是一种新的度量方法,定义为将一棵树转换为另一棵树所需的“局部移动”的最小数量,具有二次时间复杂度。文献[10]提出了一种基于映射的匹配算法,预先得出2棵本体树的节点之间的相似度,然后使用基于编辑操作的映射理论将2棵树转换成同构树,最终得到2个本体之间的最大相似度和最佳匹配对。文献[11]将网页评论的识别与自动提取转化为DOM树结构中的子树循环体识别问题,提出一种基于网页DOM子树相似度计算的方法,从网页中〈BODY〉节点向下逐层遍历识别出满足约定条件的评论块节点树。文献[12]提出一种基于加权频繁子树相似度的网页评论信息抽取方法WTS。首先通过视觉特征对网页进行剪枝处理;然后利用深度加权的相似度度量方法抽取最佳频繁子树;最后通过子树对齐方法抽取评论路径并解析评论内容。
上述算法共同之处在于都是直接计算树的相似度,但如果树的规模较大,那么聚类将是一项很费时的工作。受文献[13]的启发,本文提出基于树结构特征计算相似度的方法,构造出K个节点的所有非同构形态的子树,并计算这些子树的同构个数,将其作为特征向量来进行树的相似度计算。
1 树和树的同构
树是由n(n≥0)个节点构成的有限集。可由如下递归方式定义一棵树:
1)在任意一棵非空树中,有且仅有一个特定的称为根的节点。
2)当n>1时,其余节点可分为m(m≥0)个互不相交的有限集T1,T2,…,Tm,其中每一个集合本身又是一棵树,并且T1,T2,…,Tm称为根的子树。
树又可分为有序树和无序树。顾名思义,有序树即孩子节点之间存在确定的次序关系,无序树则相反。本文的研究是基于无序树展开的,如无特别说明,下面提及的树都是指无序树。
树是图的特殊表现形式,因此,也可以用图的定义来描述一棵树。
定义1(树) 令LV和LE分别是节点和边的有穷或无穷字母集合,树t是一个满足下列条件的四元组t=(V,E,u,v):
1)V是有限的顶点集;
2)E∈V×V是边集;
3)u:V→LV是顶点属性映射函数;
4)v:E→LE是边属性映射函数;
5)根节点入度为0,其余节点入度为1。
以树的定义为基础,下面给出子树的定义。
定义2(子树) 令t1=(V1,E1,u1,v1),t2=(V2,E2,u2,v2),t1是t2的子树,表示为t1∈t2,当且仅当下列条件成立:
1)V1∈V2;
2)E1∈E2;
3)对任意u∈V1,存在u1(u)=u2(u);
4)对任意e∈E1,存在v1(e)=v2(e)。
树t1和t2的一致性,通常需要由一个映射函数来建立,将树t1映射到树t2上,即树的同构。
定义3(树的同构) 令t1=(V1,E1,u1,v1),t2=(V2,E2,u2,v2),树的同构是一个双射,f:V1↔V2,当且仅当下列条件成立:
1)对任意u∈V1,存在u1(u)=u2(f(u));
2)对任意e1=(u,v)∈E1,存在边e2=(f(u),f(v))∈E2且v1(e1)=v2(e2);
3)对任意e2=(u,v)∈E2,存在边e1=(f(u),f(v))∈E1且v1(e2)=v2(e1)。
两棵树同构,要求它们的属性和结构上具有完全的一致性,即对于第一棵树的每一个节点和第二棵树的每一个节点之间具有一对一的对应关系,同时保证边结构保留完整,以及节点和边的属性一致。本文主要着眼于树的结构,对树节点和边的属性没有涉及,弱化了树的同构的定义,只考虑树的节点间一对一的对应关系和边结构的完整性,未考虑节点和边的属性一致。
定义4(子树同构) 令t1=(V1,E1,u1,v1),t2=(V2,E2,u2,v2),从t1到t2的一个单射f:V1→V2称为子树同构,当且仅当存在子树t∈t2使得f是t与t1的一个同构。
根据子树同构的定义,本文提出子树同构个数的概念,即求从t1到t2的单射f:V1→V2的个数。
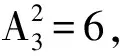
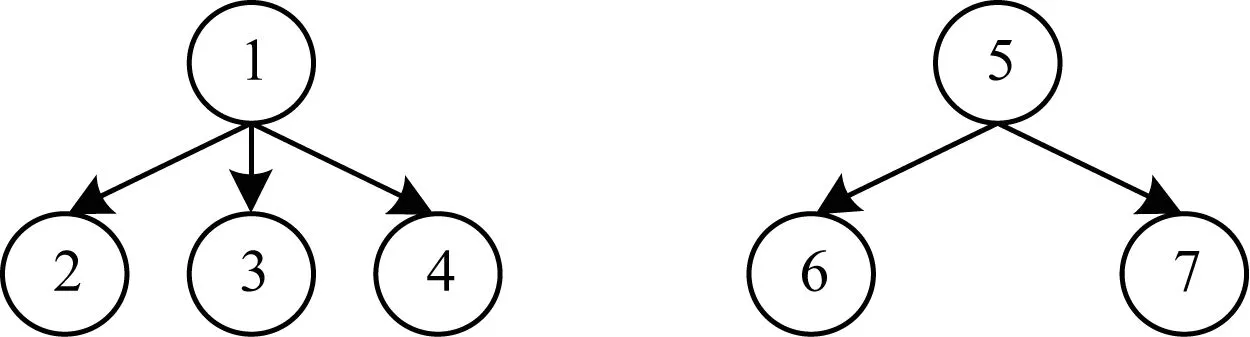
图1 子树同构个数示例
2 树的相似度计算
本文采取的是提取树特征的方式进行树的相似度计算。首先枚举出所有K子树tK(节点数为K)的非同构形态如图2所示,设tK个数为m,而需要进行特征提取的树记为T。
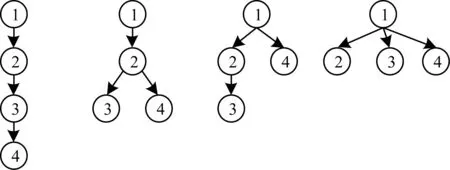
图2 K=4时tK的4种非同构形态
算法需要计算在T中tK1~tKm所有子树的同构个数,而这些计数则可构成T的特征向量A。进行树的相似度计算和聚类都可以用A进行。下面将介绍树的构建和tK在T中同构子树个数的计算方法。
2.1 同构子树算法
设tK的根节点为RtK,则本文需要将RtK和T中所有的节点进行比较,将每一次计算出来的同构个数进行累加,最后累加的结果就是tK在T中的同构子树个数。而每一次根节点之间的比较又可分为两部分的乘积:一部分是RtK的叶子节点和RT的孩子节点的对应结果,另一部分是RtK的非叶子孩子结点和RT的非叶子孩子结点的对应结果。T中某一节点RT和tK的根节点RtK的比较过程如下:
输入T中某一节点RT和tK的根节点RtK
输出RtK在RT中的同构子树个数
IsoSubtCnt(RT,RtK)
Begin
1.DT=RT的出度;
2.DtK=RtK的出度;
3.DT0K=RT中为叶子节点的孩子节点个数;
4.Dt0K=RtK中为叶子节点的孩子节点个数;
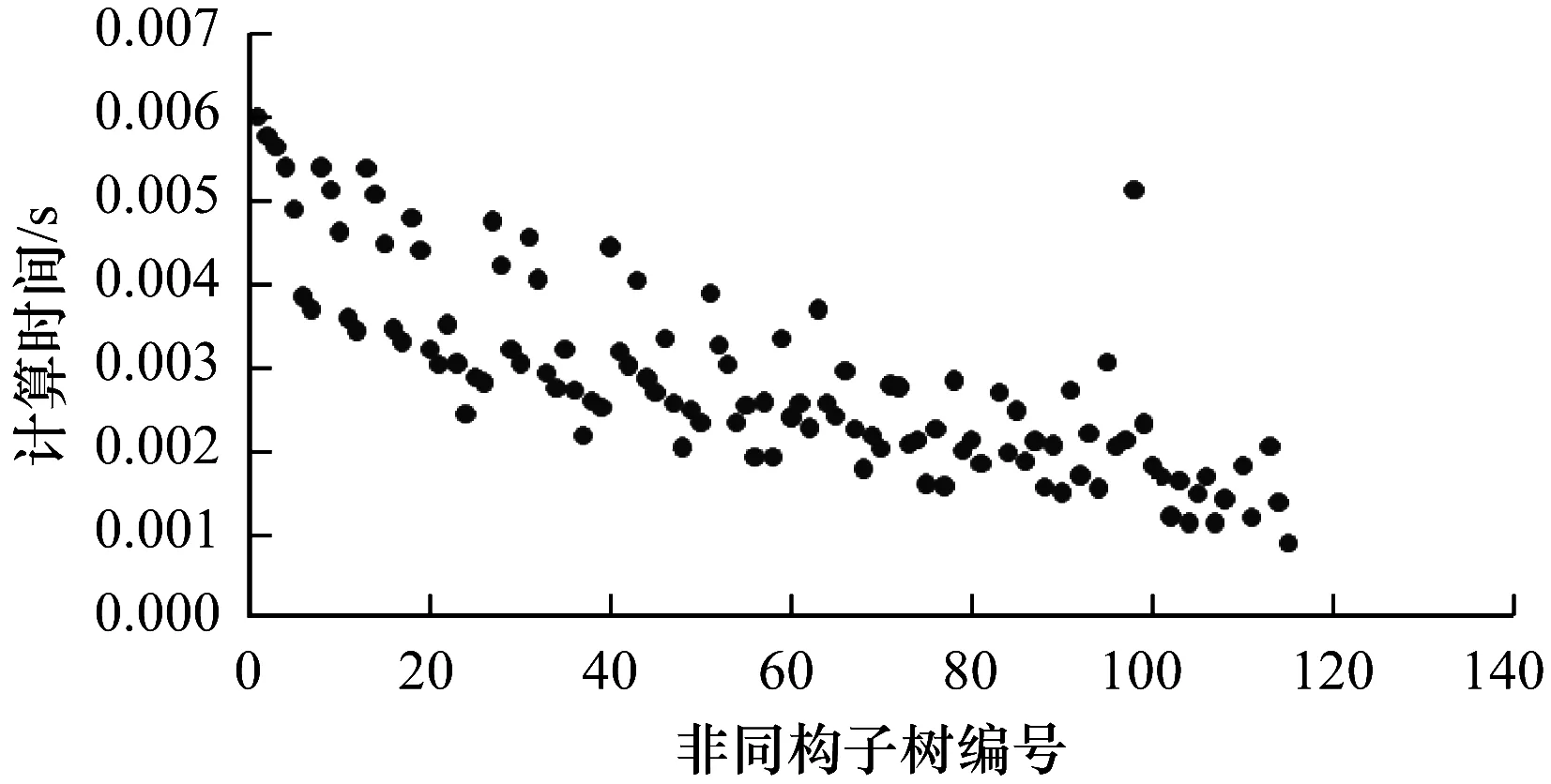
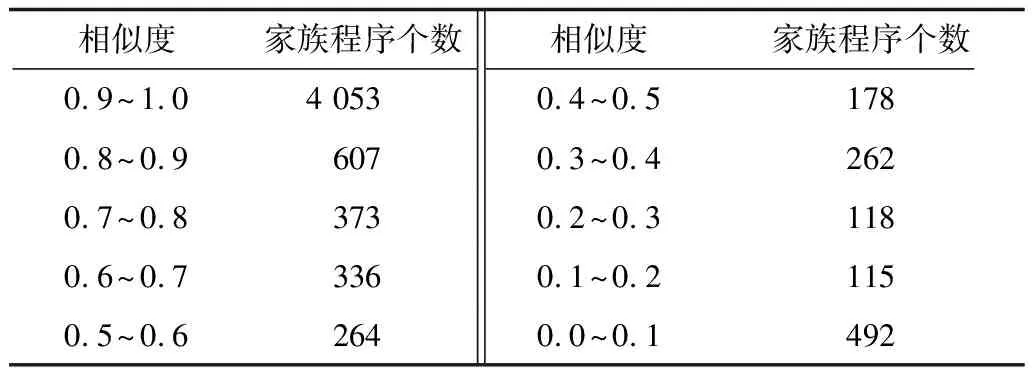
5.IFDT 6.RETURN 0; 8.I=DtK-Dt0K; 9.J=DT-DT0K; 10.TmpPart2[I][J] = {0}; 11.FOR i from 1 to I: 12.FOR j from 1 to J: 13.TmpPart2[i][j]=IsoSubCnt(RTi,RtKj); 14.END FOR j; 15.END FOR i; 16.ResultPart2=Comb(TmpPart2,I,J); 17.RETURN ResultPart1*ResultPart2; 输入TmpPart2 输出RT和RtK的所有非叶子孩子结点的对应关系个数 Comb(TmpPart2,I,J) 1.Val=0; 2.First=TmpPart2[0][],记录第0行; 3.delete TmpPart2[0][],删除第0行; 4.FOR j from 1 to J: 5.delete TmpPart2[][j],删除第j列; 6.Val += First[j] *Comb(TmpPart2,I-1,J-1); 7.restore TmpPart2[][j],恢复第j列; 8.END FOR j; 9.RETURN Val; End 由上述比较过程可知,RtK在RT中同构子树的数目由RtK的叶子节点和非叶子孩子结点在RT中的对应关系组合而成。而叶子节点的计算不需要2棵树叶子节点的一一对应,只需计算RT中能够提供给RtK叶子节点匹配的数目,从中选出Dt0K个并进行全排列即可;非叶子结点孩子的计算则需要2棵树非叶子结点的一一对应,并进行组合。 在同构子树个数的计算过程中,设RT和RtK比较时间复杂度为TC(RT,RtK),RT的非叶子孩子结点数为m,RtK的非叶子孩子结点数为n,则: (1) TCh=XTh-1+Y (2) 根据上述同构子树个数计算算法,可以得到一组关于T的特征向量,利用其进行树的相似度计算。根据实验的数据属性,可以采用不同的计算相似度的方法。根据本次实验的数据特征,每一棵子树同构数目差别较大,因此,采用式(3)定义向量间的相似度。 (3) 其中,A、B为2组特征向量,长度为n,Ai、Bi代表特征向量第i维的值,min(Ai,Bi)为Ai、Bi中较小的一个的值,max(Ai,Bi)则相反。 本文采用的实验数据来自安卓应用市场下载的23 529个安卓APK文件。这些安卓应用是分家族的,也就是一个应用有多个版本。经过反汇编后得到应用程序的函数结构调用图,并将其转换成树的形式。本文的实验目的是测试算法在实际数据上的性能,并验证相似度高的2个应用为同一家族。 经过对实验数据的预处理,得到的信息如表1和表2所示。 表1 23 529棵树的节点出度 表2 23 529棵树的节点个数 本文取K=8,记录下每一棵树提取特征所需时间,并记录下计算每一种子树形态tK所需时间。K=8时,共有115种非同构子树形态,如图3和图4所示。在图3中,有5组数据没有在图中展示,分别为:14 600~14 700时的94.6;18 000~18 100时的233.5;19 500~19 600时的120.6;19 700~19 800时的158.9;20 500~20 600时的160.1。在图4中,有3组数据没有在图中展示,分别为:82时的0.040 0;109时的0.037 8;112时的0.039 6。 图3 树节点个数与特征提取时间的关系 图4 不同形态子树的计算时间 图5 编号为82、109、112的子树共同包含的结构 为比较算法性能的优劣,本文选择了开源工具igraph来计算同构子树的个数。在igraph中有提供函数igraph_count_subisomorphisms_vf2,即用VF[14]算法演变而来的VF2算法[15]来计算同构子树的个数。VF2算法是目前较为优秀的同构子图计算算法之一,是VF算法的扩展,与同类算法相比,有较优的时间复杂度和空间复杂度。由于目前并没有子树同构个数计算算法,因此本文将VF2算法作为比对算法,检验本文算法的性能提升。由于VF2算法在某些情况下计算时间太长,因此本文只挑选了1组数据进行计算。该组数据有513个节点,最大节点出度为53。实验结果如图6所示。 图6 本文算法与VF2算法的时间性能比较 由图6可以看出,VF2算法计算115棵同构子树的个数花费时间为3 430 s,而本文算法花费时间0.132 8 s,VF2算法中93.9%的子树运行时间远在本文算法之上。在VF2算法花费时间较长的子树的特征中,最明显的就是115号子树,如图7所示。 图7 编号为115的子树形态 这些子树的共同特征是具有较多的叶子节点,而树T中一些节点出度较大。VF2算法需要枚举出所有的叶子节点的映射关系,导致了算法运行时间增大。可以看出本文算法在子树同一层叶子节点较多的情况下优势明显。 本文按照式(3)对23 529个特征向量进行了相似度计算。这些特征向量分属6 799个类别,即有6 799类安卓家族程序。相似度比较结果如表3和表4所示。 表3 6 799类安卓家族程序族内相似度比较 表4 23 529个安卓程序族间相似度比较 由表3可以看出,在6 799个家族中,相似度较高的家族程序所占比例较大,相似度在0.7以上的占比达74%。本文查看了相似度较低的家族程序提取的特征向量,发现它们的差距确实比较大;而实际安装这些不同版本的同家族程序,发现它们之间的改动比较明显。而由表4可以看出,不同类别的安卓程序相似度都比较低,不超过0.2。这一方面说明同家族的程序相似度较大,不同家族的程序相似度较小,而本文提取的特征向量能较好地反映程序间的相似度;另一方面显示出某些家族程序改版较大,这也符合实际情况。 现阶段,不少学者对树的相似度计算都是通过直接比较两棵树的特征进行的,但是都不能很好地处理数据量较大的情况。本文基于文献[13]的研究,通过树的结构特征来进行树的相似度计算。实验结果显示:随着树规模的增大,算法时间复杂度并不是呈指数增大,而是线性增大,这说明本文算法能够适用于规模较大的数据;在相似度计算方面,同类家族的程序相似度较高,相似度在0.7以上的家族程序占比达74%;不同类家族的程序相似度较低,相似度不超过0.2,这也说明了程序的相似度可以用提取的特征向量的相似度来表示,而有的家族程序的相似度较低,说明这类程序在某一版本之后做了较大的改动,导致程序结构调用图有了较大的变化。上述结果均表明提取的特征向量能高效准确地用于树的相似度计算。下一步将研究本文算法在恶意软件检测、网页结构特征抽取等场景应用的情况,同时提高算法的实用性。
2.2 同构子树算法的时间复杂度
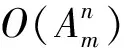
2.3 树相似度算法
3 实验与结果分析
3.1 实验数据
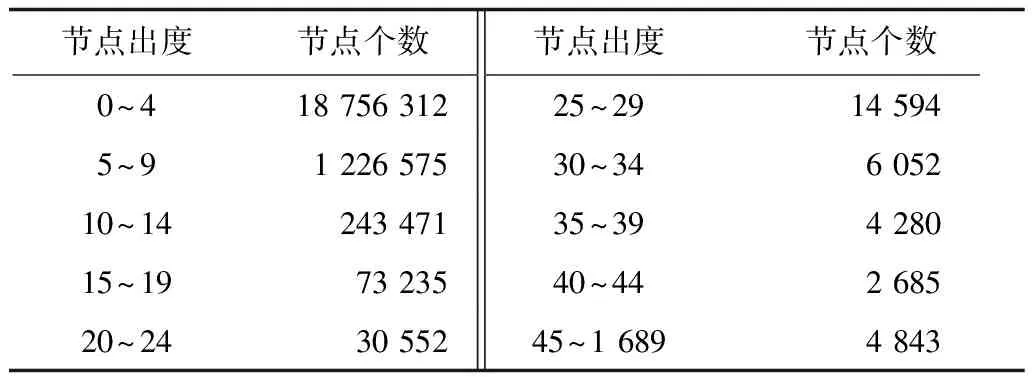
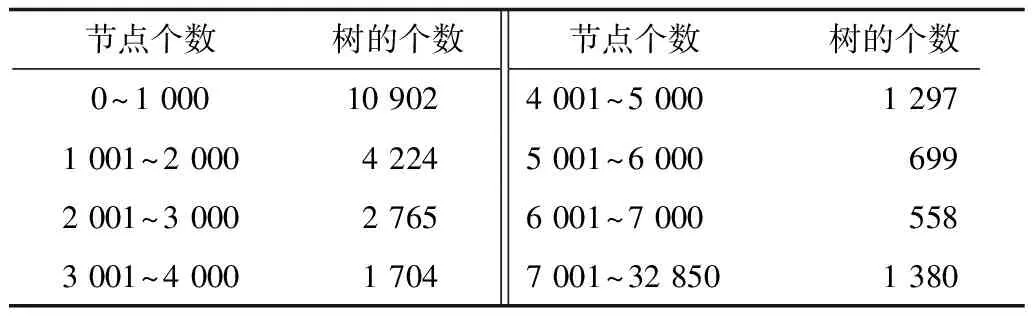
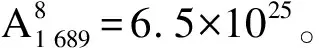
3.2 特征向量提取





3.3 相似度比较

4 结束语

