串联基本图形，提炼数学方法——以三道中考圆的典型问题剖析为例

☉山东省临清市京华中学 齐 欣

圆的内容颇具包容性，是中考综合性试题重要的考查对象.从联系的角度看，2018年中考圆的问题更加凸显解题思路和方法的典型性和综合性.解决圆的问题时，首先要熟悉图形的性质与判定，能从复杂图形中分离出基本图形，学会发现图形之间的关联；其次要能进行问题的转化与思考，应用图形的性质与判定，关注基础知识，弄清定理的条件和结论，抓住图形的特征；最后要能从已有知识和技能出发，通过合情推理主动建立相关知识之间的联系，以及对未知的问题进行深入探索，提炼数学方法，有效积累数学活动经验.

一、圆的切线判定问题，体现转化，突出模型

圆的切线问题涉及其判定和性质应用，既是重点，又是中考热点和常考考点，常和计算等相结合，突出考查基础知识，以及基本图形串联能力和数学思维能力.

例1 （2018年聊城中考卷第24题）如图1，在Rt△ABC中，∠C=90°，BE平分∠ABC交AC于点E，作ED⊥EB交AB于点D，⊙O是△BED的外接圆.

（1）求证：AC是⊙O的切线；

（2）已知⊙O的半径为2.5，BE=4，求BC、AD的长.

方法点拨：当所判断的直线与圆有明确公共点时，通常是利用切线的判定定理，即经过半径的外端且垂直于半径的直线是圆的切线，应用时需要确定这条半径，证明垂直关系.可连接OE，再证明AC⊥OE.如果未明确直线与圆的公共点，则需要过圆心向这条直线作垂线段，证明其长度等于圆的半径，即利用“平面内到圆心的距离等于圆的半径的直线是圆的切线”.

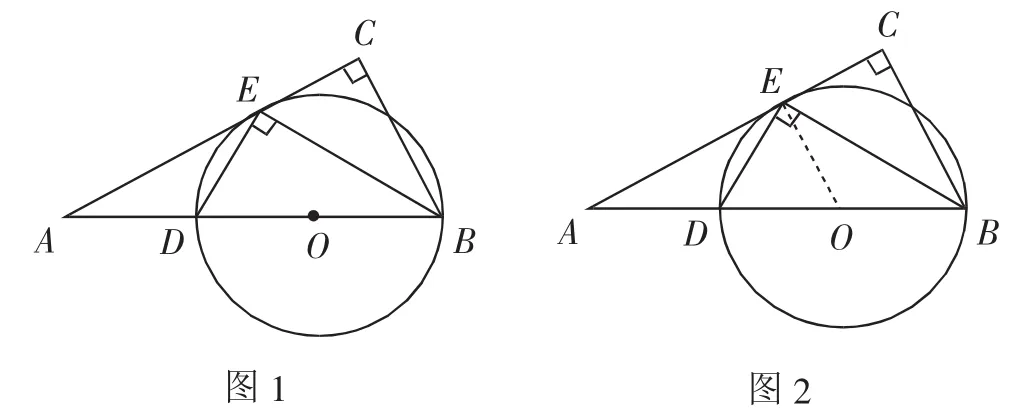
（1）证明：如图2，连接OE.

因为OE=OB，所以∠OEB=∠OBE.

因为BE平分∠ABC，所以∠OBE=∠EBC.

所以∠OEB=∠EBC，所以OE∥BC，所以∠AEO=∠C.又因为∠C=90°，所以∠AEO=90°，所以AC⊥OE.又AC经过半径OE的外端E，所以直线AC是⊙O的切线.

（2）解：因为⊙O的半径为2.5，所以OE=2.5.

因为圆周角∠DEB=90°，所以弦BD是⊙O的直径，从而BD=5.

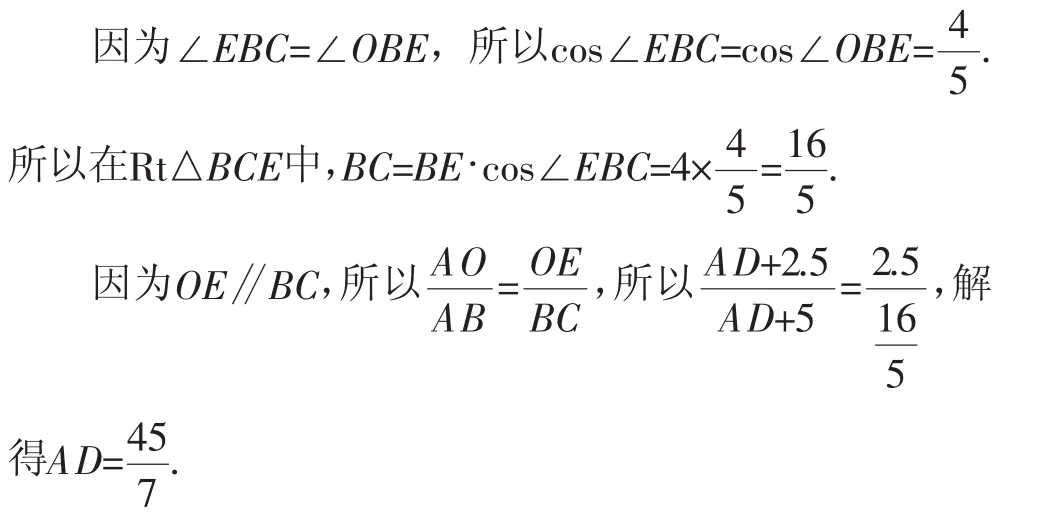
点评：此题虽然简单，卡点在于做第（2）问时，学生很容易忽视应该说明BD为直径；还有就是推出AC⊥OE后，没有说明AC经过半径OE的外端.有关圆的切线的判定和性质，添加半径，是推理计算的关键；构造直角三角形，应用锐角三角函数或三角形相似、勾股定理、图形面积、平行线分线段成比例等知识更是解决计算问题的常用手段.最后，要形成解决这类切线问题的常用思路，积累数学活动经验，提炼数学模型，提高学生的数学素养.

二、借助弧、平行线等导角，体现最近联想，展现合情推理

弗赖登塔尔反复强调：学习数学唯一正确的方法是实现再创造.在数学创造中，最近联想和合情推理能力很重要.下面以一个圆的问题为例，挖掘条件，说明如何导角.

例2 （2018年福建中考卷第24题）如图3，四边形ABCD内接于⊙O，AC为直径，DE⊥AB交AB于点E，交⊙O于点F.

（1）延长DC、FB相交于点P，求证：PB=PC.

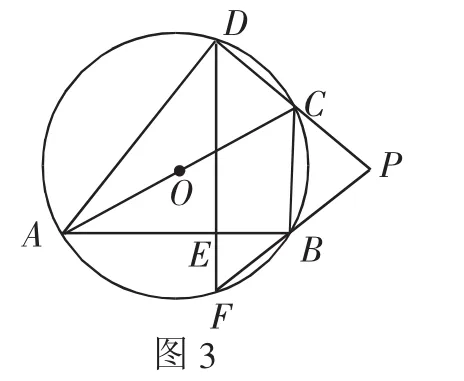
方法点拨：借助圆内接四边形的外角等于内对角，连接AF、CF，可以轻松解决第（1）问，这是方法1.还可以连接BD、CF，借助BC∥DF及圆周角定理，转化为证∠PDF=∠PFD，这是方法2.也可以利用垂径定理的推论“两条平行弦所夹的弧相等”得到弧CD与弧BF相等，进而得到CD=BF，再利用平行线分线段成比例这一性质解决，这是方法3.在第（2）问中，四边形BCDH是一个平行四边形，从而BC=DH=1，借助∠BDE→∠DBE→∠DCA（连接OD）→∠DOC→∠COH（设AC、DE的交点为N）→∠ONH→∠ACB，结合，DH=1，转化为在Rt△ACB中，求∠ACB的度数.

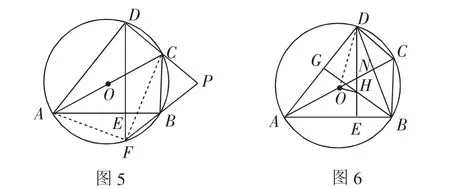
解：（1）如图5，连接AF、CF.

因为四边形ABCD内接于⊙O，所以∠BCP=∠BAD.同理，∠CBP=∠CAF.

因为DE⊥AB，所以∠AED=90°，从而∠BAD+∠ADF=90°.

因为AC为直径，所以∠AFC=90°，所以∠CAF+∠ACF=90°.

又∠ADF=∠ACF，所以∠BAD=∠CAF，所以∠BCP=∠CBP，所以PB=PC.

（2）如图6，连接OD.

因为AC是⊙O的直径，所以∠ADC=90°.

因为BG⊥AD，所以∠AGB=90°.

所以∠AGB=∠ADC，所以BG∥DC.

同理，BC∥DE.

所以四边形BCDH为平行四边形，所以BC=DH=1.

因为BC∥DE，所以∠ONH=∠ACB=60°.又∠OHD=80°，所以∠COH=40°，所以∠DOC=40°，所以∠DCO=70°，所以∠DBE=70°，从而∠EDB=20°.

点评：既然直径AC=2，那么半径OD=OC=1，而DH=1，所以DO=DH，从而∠ODH=20°，因此对于第（2）问，还可以利用方程来解决.设∠EDB=x度，则∠DAO=∠ADO=60-x-20=（40-x）度，从而∠DOC=2（40-x）度.而∠ODC=∠OCD=∠DBE=（90-x）度，在△ODC中，由三角形内角和定理，得2（40-x）+2（90-x）=180，解得x=20.事实上，第（2）问把、DH=1换成DH，仍可以求出∠EDB的度数，以此揭示问题的本质.

三、挖掘问题数学本质，在数学活动中关注核心素养

数学活动的关键是启发学生学会数学思考.史宁中教授指出数学活动的基本路径是把握数学本质，通过恰当的数学问题，启发学生学会数学思考，让学生在掌握知识和技能的同时，形成和提升数学核心素养.

例3 （2018年武汉（中考卷第10题）如图7，在⊙O中，点C在优弧AB上，将沿BC折叠后刚好经过AB的中点D.若⊙O的半径为，AB=4，则BC的长是（ ）.

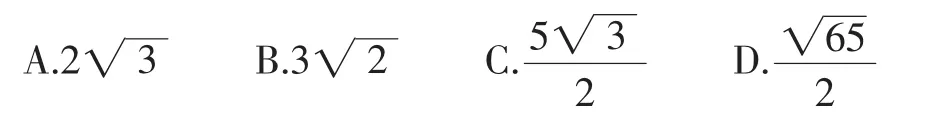
方法点拨：本题考查的是圆周角的等量代换，三角形和四边形问题.明确这个很重要，它是解题时思考的方向和关键.根据过“AB的中点D”联想到“垂径定理”（连接OD，则OD⊥AB），再连接OA，由勾股定理求得OD=1.所在的两个圆是等圆，联想“同圆或等圆中相等的圆周角所对的弧相等”可知圆周角∠BCD所对的两条弧相等，连接AC、CD，可得AC=CD.接下来，可以作CE⊥AB，求得BE=3，AE=DE=1，在直角梯形CEDO中知道上底和两腰，如何求下底？利用“加高法”作OF⊥CE即可（如图8）.

还可以连接OD，并延长DO交BC于E，作直径AD′，则∠ABD′=90°，OD=1，连接BD′，作OF⊥BC，得BC=2BF.易求BD′=BD=2，所以弧BD=弧BD′，从而弧CD=弧CD′，∠ABC=∠CBD′=45°.在Rt△EDB中，ED=BD=2，EB=，从而OE=1，所以，所以BC=

点评：《义务教育数学课程标准（2011年版）》指出，试题要注重对基础知识和基本技能的考查，考查学生理解数学本质，考查学生能否在具体情境中合理应用.画图，在图形上标上数据，这是很重要的一个环节.本题有多少种解法并不重要，你需要知道的是有多少知识点对应多少路可走，然后选择下意识想走的那一条即可！压轴题并不意味着它有多复杂，有多少条辅助线，有多少技巧性的解法，它更多要考查的是考生的素养.基于核心素养的教学，要把握知识本质、创设教学情境，基于核心素养的评价更关注思维品质、注重考查思维过程.

数学抽象是数学的基本思想，是形成理性思维的重要基础，反映了数学的本质特征，贯穿在数学的产生、发展、应用过程中.数学教师要站在联系、发展的角度探寻数学中典型问题的生长点、延伸点，以数学思想方法为核心，以能力考查为目标，创造更多源于课本的，给人以启迪，让每个学生都得到充分发展的好的数学问题.