基于原有认知，培养实践意识——新课标背景下初中数学教学实践与反思

☉江苏省启东市百杏中学 浦圣妹

新课标提出发展学生的核心素养，培养更全面的人.那么，对于初中数学教学而言，我们的课堂应该如何变化呢？笔者认为应该更注重学生的学习基础，应该丰富学生的体验，有意识地培养学生的实践意识，增强学生的过程体验.本文以无理方程的教学为例，就如何具体地实施谈几点思考.

一、创设情境，引导中生成概念

学生都是带着知识和经验学习知识的，在学习无理方程之前，学生知道方程，也会“列方程”，为此，我们我们可以从学生的基础出发设置问题情境，采用实验和师生对话的方式引出无理方程及无理方程的概念.

实验情境：老师给每组同学提供了一根30cm长的细铁丝，现在大家尝试着将其弯折成一个直角三角形，要求有一条直角边长为5cm.

设计意图：这是一个实践类的问题，学生不加思索，借助于三角板的直角是可以实践的，但是在弯折的过程中会出现困难，即另外一条直角边从何处开始“弯折”.继而生成新的问题.

生成问题：如何求另外一条边长？

出现了一个未知量，要解决这个问题，学生很自然地会想引入未知数.通常情况下，学生会想到设另一直角边长度为x cm，借助于勾股定理，学生能够列出方程：52+x2=（30-5-x）2，即52+x2=（25-x）2（1）.

能列出方程（1）是学生的认知基础，不仅如此，从该方程中学生还能够得到斜边长为此时，可以采用追问的方式进一步引导学生思考.

追问1：除了方程（1），大家还能列出怎样的方程？

设计意图：学生从总长度为30cm、一条直角边长为5cm出发，很自然能够联系到斜边长度应该为30-5-x=25-x，可以得到新的方程：（2）.

追问2：大家观察方程（2），从我们的原有经验出发，想一想：方程（2）的左、右两边分别指的是什么？猜一猜这样的方程有什么意义.

设计意图：追问2是将学生得到方程（2）的思维可视化，方程（2）的左、右两边均可以表达弯折出来的直角三角形的斜边，继而很自然地归纳方程的实质，即建立等号、列方程的意义，从两个不同侧面对数学问题中同一个量进行表达.当然，同一个数学问题的思考点可以不一样，找到的同一个量也会不同，可以进一步追问，促进学生对上述认识的理解.

追问3：上述问题，如果我们换一个角度，你还可以列出怎样的方程？

二、基于生成，比较中深化理解

学生的生成是课堂探究的重要生长点，通过前面的情境创设和引导，学生得到了3个方程，这里有有理方程和无理方程，我们在课堂上引导学生对这3个方程进一步进行比较，能够深化学生对无理方程的内涵的理解，自主比较得到无理方程的本质特征，印象会更深刻.

师：观察（1）、（2）、（3）三个方程，你觉得和我们前面学习的方程有怎样的差别？

设计意图：方程得到后，学生会发现含有根式且根式下的内容是包含未知数的代数式，以前没学过，这属于学生感兴趣的地方，如果我们直接灌输给他们，则印象不深刻，引导学生自己去发现更能够深化学生对无理方程概念的理解，在学生有了初步判断后，再抛出一些方程让学生辨析，能够促进概念的理解与内化.

练习：判断下述方程哪些属于关于x的无理方程.

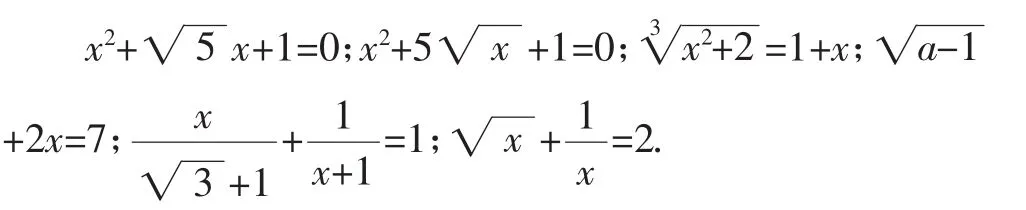
在学生在辨析的过程中有了一定认识后，再进一步引导学生讨论前文中涉及的3个方程，将学生的思维点转移到此类方程如何解的探寻中来.

师：我们大家再来观察前面得到的三个方程，看看（2）和（3）之间存在的联系，（1）和（2）之间存在什么联系？

设计意图：学生再一次对方程进行比较，比较的过程就是实践的过程，而且行有所获，最终学生会发现代数式的变化过程，将方程（3）等价变形可以得到方程（2），将方程（1）的两边同时开方可以得到方程（2），在此基础上，为了防止学生的思维出现片面性，可以进一步追问.

追问4：若a2=b2，则a=b，大家觉得这一判断对吗？

设计意图：学生前面思维出现障碍，如果我们直接灌输正确的结果可能印象不深，下次还是会错，怎么办？借助于追问4，学生在分析：如果a2=b2，有a=b或a=-b两种情况时，很自然地就会发现前面的说法“方程（1）两边同时开方可以得到方程（2）”是有问题的.

追问5：那么应该怎么说呢？若a=b，则有a2=b2，这样说对吗？

学生有了上述思考，对于如何解无理方程就清晰了：将方程两边平方，将其转化成有理方程再求解.

三、实践体悟，引导在应用中感悟

数学概念的学习离不开应用过程，应用的过程是实践，是进一步培养和发展的过程，前面对概念的理解程度和思维状态都会在概念应用的过程中暴露出来，并有新的感悟.

1.设置例题，感悟方法

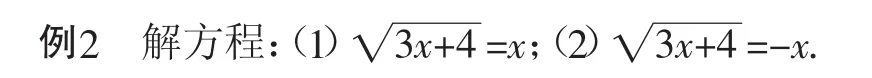
设计意图：例2给出的是两个不同的方程，但是最终的根是一样的，自然地将思维转向：这里面有怎样的关联呢？促进学生进一步比较与思考，很快在观察与比较中感悟到方程的非同解变形会使方程根的范围扩大，此时怎么办？很自然地生成验根的需要，这恰恰也是我们教学的重点、难点所在.

2.自主练习，比较“通法”和“巧法”

我们在数学教学的过程中，要谨防学生出现思维定式，同时要注意对学生发散性思维的引导，对于解无理方程而言，我们通常的方法是“平方法”，这样的通法在教学中当然要练习和巩固，但不要将“平方法”作为唯一路径，要渗透巧法，让学生的思维品质获得有效提升.

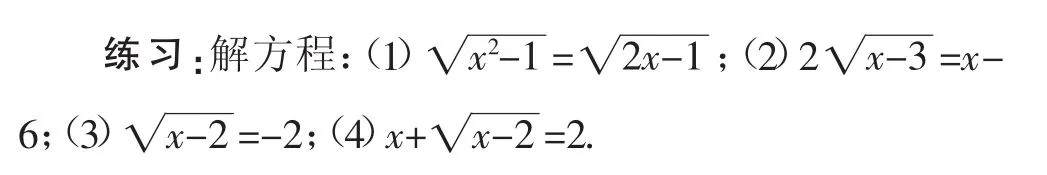
设计意图：上述四个方程，学生借助于平方法很快可以解决，从学生完成的情况看，我们要提醒学生对于第（2）小题，不能把“2”的平方疏忽掉；在解决（3）、（4）两个特殊的无理方程时，学生如果进行简单的平方就容易出现问题，学生在自主尝试并解决问题后，对解决无理方程的方法会有新的感悟，这是我们帮助学生有效克服思维定式负迁移的最好办法.

四、总结归纳，引导学生在联想中关联

知识之间是有联系的，我们每学习一个概念和方法，都应该引导学生将其归纳到原有的认知结构之中，在联想中关联，促进数学知识结构的建构式发展.

1.类比分析化归思想

这节课的学习，我们可以引导学生总结，得出结论，如图1所示.

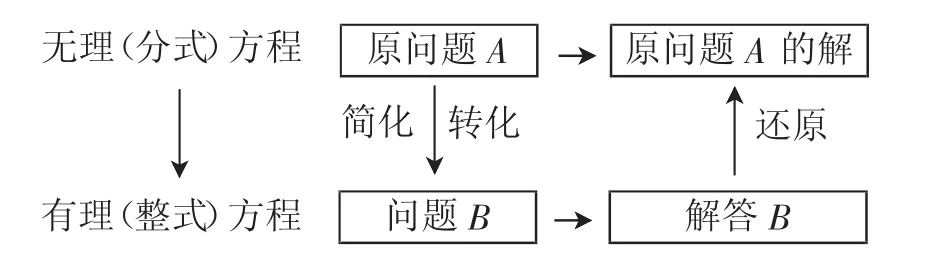
图1

2.引导学生在“方程”和“式”的比较中感悟知识内在关联，比较中得出方程的知识结构.

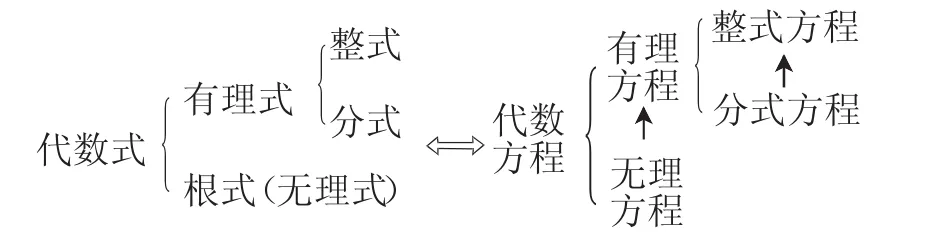
图2

教育家马登曾经发表过学习就是鉴别的著名观点，鉴别又必须建立在比较的基础之上，学习者自身必须具备一定的认知，才能从物质的、文化的、感知的世界中对某些特征进行辨认和察觉.笔者认为，初中数学教学，就应该让学生在原有认知的基础上进行“比较”，这是发展学生认知和实践意识，提高学生解决实际问题能力的不二法门.