基于双边知识匹配的产品开发任务分配方法
陈友玲,赵金鹏,兰桂花,黄 典
重庆大学 机械传动国家重点实验室,重庆 400044
1 引言
随着市场竞争的日趋激烈和科学技术的快速发展,客户需求越来越多样化、个性化,导致产品复杂程度日益增大,产品开发势在必行。通常,产品开发任务由一系列子任务组成,需将其合理分配给多部门、多领域的多名开发人员协作完成,故每项子任务的完成情况都将对整个产品开发过程产生重要影响。因此,在产品开发阶段,将合适的子任务分配给合适的人员是产品开发管理中的重点研究内容[1]。
目前,国内外众多学者对产品开发方法和任务分配与调度做了大量的研究。文献[2]通过分析迭代产品开发过程,结合Markov过程建模方法与蚂蚁算法,提出混合蚁群算法,应用于产品开发过程的优化求解;文献[3]针对新产品开发方法选择过程的研发结果与市场环境的不确定性,计算不同市场的预期收益,并构建效用函数以计算新产品开发方案的综合效用值来获得最优产品开发方案;文献[4]提出大数据驱动下的客户参与的产品开发方法,给出关键实施流程,构建产品开发的三阶段实施流程,以提高产品创新能力和质量水平;文献[5]针对复杂产品开发流程,构建了动态模式下的产品开发思路与方法,并提出基于信息资源库和决策方法库的技术支持系统,以实现复杂产品开发的技术与管理的融合;文献[6]考虑产品开发的竞争方案信息,对比产品开发方案与竞争产品方案的前景绩效参考值,构建前景价值函数与目标函数,以实现产品开发的优化选择。文献[7]提出了一种具有多技能员工和多模式产品开发项目的任务分配方法,最大限度地减少了项目的持续时间,并平衡了工作人员参与项目的工作量;文献[8]提出了一种基于疗效矩阵的多属性效用函数,以提升任务分配在航天航空工业中的可靠性;文献[9]提出了一种集成数字设计结构矩阵的自适应遗传算法,以实现客户协同任务分解与分组;文献[10]提出了一种基于神经网络增强学习算法的工艺任务分配方法,以提高工艺设计效率;文献[11]在综合考虑协同定制产品开发流程和任务分配策略的基础上,提出了一种基于双种群自适应遗传算法的协同定制产品开发任务分配优化方法。
现有针对产品开发的研究主要集中于开发方法与支持系统等方面,而对产品开发任务分配主要集中于任务的需求-能力的匹配,基于神经网络、遗传算法等思路进行任务与人员的单向匹配。上述方法都为产品开发任务分配提供了新的思路,但存在以下不足:
(1)产品开发任务分配本质上是使具备相应知识的人员获得相应子任务,而上述方法多是从任务层面进行直接分配;
(2)人员是任务的具体执行者,而上述文献仅仅单边考虑人员是否适合任务,忽视人员与任务之间的双向匹配,势必造成人员对任务满意度的下降,影响任务完成的成本、质量、效率等;
(3)自适应遗传算法、神经网络等技术难度大,操作复杂。
虽然产品开发任务类型多变,分配不易,但产品开发任务分配均基于知识匹配,不同的知识匹配对应不同的人员匹配;此外,人员是任务具体执行者,其自主选择子任务,将有效改善任务执行成本、质量及效率等。基于以上两点,本文从任务和人员双边的角度考虑知识匹配,提出了一种基于双边知识匹配的产品开发任务分配方法。该方法充分考虑了任务知识需求和人员知识结构,以双方知识匹配最佳、满意度最大为目标,构建产品开发任务分配数学优化模型,最后采用基于隶属函数的加权和法将多目标数学模型转化为单目标数学模型,并采用Hungarian算法对模型进行求解,最终获得产品开发任务分配方案。
2 问题描述
2.1 问题定义
假设某产品开发任务由m项子任务组成,n名开发人员完成,子任务集合为T={T1,T2,…,Tm} ,Ti表示第i项子任务,I={1 ,2,…,m},i∈I,人员集合为 P={P1,P2,…,Pn},Pj表示第 j个人员,J={1 ,2,…,n},j∈J 。产品开发任务分配的目标:寻找一个最优任务分配方案,将m项子任务合理分配给n名人员,使任务和人员双边知识匹配达到最佳,双方满意度最高。在产品开发任务分配过程中,人员知识能力对任务分配方案具有重大影响,人员知识能力与任务知识需求越匹配,任务对人员的满意度越高,任务完成质量就越高;同时,任务知识需求对任务分配方案也影响重大,任务知识需求与人员知识兴趣越匹配,人员对任务的把控能力越强,任务完成质量也越高。在评价人员知识能力与任务知识需求匹配程度之前,有必要对人员知识能力和任务知识需求进行测评。
2.2 基于模糊集理论的人员知识能力评价
人员知识能力是反映人员吸收知识、运用知识和转化知识效率的重要指标,其内涵是人员具有的各种以知识为核心要素能力的综合[12]。人员知识能力分为显性知识能力和隐性知识能力。这里的显性知识能力特指与产品开发任务密切相关的知识能力,可清晰表达,测评者亦可直观获得,本文以决策系统知识库的历史数据作为显性知识能力测评依据。而隐性知识能力由于具有“内隐”和不易获取的特性,测评较困难,本文采用基于模糊语言评价集的Delphi法对隐性知识能力进行描述和测评[13]。
假设待测评人员集为P={P1,P2,…,Pn},Pj表示第j个人员,参与测评的专家集为D={D1,D2,…,Dl},Dk表示第k个测评专家。假设每名专家的重要程度均相同,隐性知识能力测评指标集为C={C1,C2,…,Cg},Cp表示第p个隐性知识能力测评指标,显性知识能力测评指标集为K={K1,K2,…,Kh},Kq表示第q个显性知识能力测评指标。专家Dk针对隐性知识能力指标集C的各项指标给出的权重向量和测评矩阵分别为wk=和 X。其中,表示专家Dk给出的指标Cp的权重表示专家Dk针对人员Pj对应于指标Cp给出的测评结果。由于隐性知识具有不可度量性,故和均以模糊语言评语集的形式给出。其中,模糊语言评语集采用7粒度语言变量集:S={S1=AP(非常差),S2=VP(很差),S3=P(差),S4=M(中等),S5=G(好),S6=VG(很好),S7=AG(非常好)},对应语言变量用梯形模糊数表示为(0,0,0.1,0.2),(0.1,0.2,0.2,0.3),(0.2,0.3,0.4,0.5),(0.4,0.5,0.5,0.6),(0.5,0.6,0.7,0.8),(0.7,0.8,0.8,0.9),(0.8,0.9,1.0,1.0),记和用梯形模糊数分别表示为和。此外,决策系统根据知识库历史数据对指标集K给出人员显性知识能力测评矩阵表示人员Pj对应于指标Kq给出的测评结果。
人员知识能力测评步骤如下:
步骤1集结所有专家隐性知识能力模糊测评矩阵和指标权重向量。将所有专家给出的模糊测评矩阵集结为群体模糊测评矩阵,记,相应指标权重向量集结为群体指标权重向量wp,记wp=(ap,bp,cp,dp)。其中:

步骤2计算人员隐性知识能力模糊测评值。记人员Pj的隐性知识能力模糊测评值为uj,隐性知识能力模糊测评值向量为u=(u1,u2,…,un)T,uj=(Xj,Yj,Zj,Wj),其中:
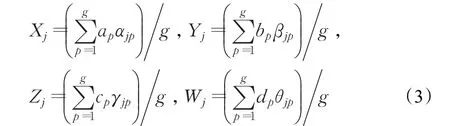
步骤3计算隐性知识能力测评期望值。人员Pj的隐性知识能力测评期望值为I(uj):

为分析方便,对其进行规范化处理,得人员Pj隐性知识能力值:

步骤4计算显性知识能力测评值。根据人员显性知识能力测评矩阵Y=[yjp]n×h得出测评值向量v=(v1,v2,…,vn)T,vj表示人员Pj的显性知识能力测评值。

经规范化,可得人员Pj显性知识能力值:

步骤5计算人员Pj的总体知识能力值:

其中,μ和1-μ为隐性知识能力和显性知识能力的重要程度。最后,根据总体知识能力值计算结果,可得每项开发任务对各开发人员的评价结果。
2.3 基于知识兴趣的任务知识需求评价
决策系统对开发人员已完成的任务进行分析归纳,获得开发人员知识兴趣,将待完成的开发任务与人员知识兴趣匹配比较,得到人员对开发任务的评价。
人员对开发任务评价主要包括以下步骤:
步骤1获取人员知识兴趣。为方便管理,将知识库内所有知识以知识项的形式存储。知识项是一个知识点与知识属性构成的二元组集合,表示为KI=(KP,KC),其中,KP表示知识点,KC=(KC1,KC2,…,KCn)表示该知识点属性值。假设D1是人员已完成的所有任务的知识项集合,KIi和KIj分别表示D1中某两个知识项,KPi和 KPj分别表示 KIi和 KIj的知识点,则 KCi=(KCi1,KCi2,…,KCin)和 KCj=(KCj1,KCj2,…,KCjn)分别表示KPi和KPj的知识点属性值,其空间向量表示为kci=(kci1,kci2,…)和 kcj=(kcj1,kcj2,…),则 kci和 kcj的属性相似度可用两个向量的夹角余弦值表示:

假设某个人员已完成的开发任务包含m个知识项,根据式(9)得每两个知识项间的属性相似度,可得每个知识项KCi的综合属性相似度为[14]:

最后得知识项KCi的偏离相似度,其计算公式为:

式中,sdmax表示所有知识项的综合属性相似度的最大值。偏离相似度反映了该知识项与所有知识项的综合兴趣相背离程度,其值越小,偏离程度越高。因此,设定一个阈值λ,若某知识项的偏离相似度大于λ,则认为该知识项属于人员的知识兴趣,最终形成人员的知识兴趣集合D2。
步骤2基于知识兴趣的任务评价。对于某一特定开发人员而言,当知识兴趣集合确定后,可将每项任务知识项集与人员知识兴趣集相比较,匹配度越高,任务开发人员越满意。匹配度不仅与知识项集的相似属性有关,也与知识项集不相似的属性相关,知识兴趣集合D2与任务知识项集D3的匹配度计算公式如下[15]:

3 基于双边知识匹配数学模型的建立
3.1 人员与任务的双边满意度
根据前文的步骤可得开发任务Ti给出的关于开发人员集合P的优先级排序结果,将优先级排序结果用序值向量 Ri表示,设 Ri=(ri1,ri2,…,rin),将rij定义为序值,表示开发任务Ti把开发人员Pj排到第rij位,rij∈J,若rij=1表示开发任务Ti将开发人员Pj排到第1位。显然,序值越小,表明开发任务对当前开发人员越满意;同理,可得人员Pj给出的关于任务集T的优先级排序结果,将其用序值向量Vj表示为Vj=(v1j,v2j,…,vmj)T,将vij定义为序值,表示人员Pj把任务Ti排到第vij位,vij∈I,若vij=1表示人员Pj将任务Ti排到第1位。显然,序值越小,表明开发人员对当前开发任务越满意。基于序值向量 Ri和Vj,可分别建立序值矩阵 R=[rij]m×n和V=[vij]m×n。
进一步,将序值转化为满意度,设φ(x)是一个关于序值rij或vij的满意度函数,该函数应满足以下性质:(1)φ(x )≥0;(2)φ(x )是一个单调递减函数,即φ′(x )<0;(3)令φ(1)=1。事实上,匹配主体双方的满意度敏感性是逐渐降低的,比如,人员对序值第一和第二的任务满意度落差比较大,但对序值第九和第十的任务满意度落差就没那么大。基于文献[16]的研究成果,本文的满意度函数采用幂函数的形式来描述主体敏感性逐渐递减的心理感受。设任务Ti对人员Pj的满意度为αij,人员Pj对任务Ti的满意度为βij,其计算公式如下:
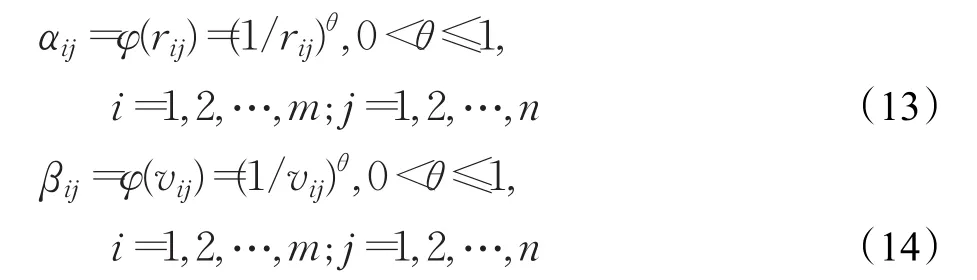
其中,θ为满意度衰减系数,0<θ<1,由式(13)和(14)可知,开始时满意度减小的速度比较快,之后逐渐变慢,符合主体敏感性递减的心理感受。根据式(13)和(14),将序值矩阵 R和V 转化为满意度矩阵 A=[αij]m×n和B=[βij]m×n。
3.2 数学模型的建立与转化
设xij表示一个0-1变量,其中,xij=0表示任务Ti未分配给人员Pj,xij=1表示任务Ti分配给人员Pj。基于满意度矩阵A和B,根据双方满意度最大的原则,可构建如下双目标数学模型:

其中,式(15a)~(15b)为目标函数;式(15a)表示尽可能使任务对人员的满意度之和最大;式(15b)表示尽可能使人员对任务的满意度总和最大;式(15c)表示每项任务必须且只能与一个人员匹配;式(15d)表示每个人员至多与一个任务匹配。
上述模型是一个多目标0-1整数规划模型,本文采用基于隶属函数的加权和方法将多目标数学模型转化为单目标数学模型进行求解[17]。两个隶属函数分别定义如下[18]:

据式(15a)和(15b),可将上述双目标优化模型转化为式(17)所示单目标优化模型。

其中,ω1和ω2分别表示目标函数Z1和Z2的权重,且0≤ω1,ω2≤1,ω1+ω2=1。为保证任务分配过程中人员和任务双方的公平性,取ω1=ω2=0.5。转换后的模型是一个典型的任务指派问题,可采用Hungarian算法进行求解。
4 算法求解流程
任务分配的算法步骤如下:
步骤1获得任务关于人员集合序值向量Ri和人员关于任务集合序值向量Vj;
步骤2根据Ri和Vj分别得序值矩阵R和V;
步骤3根据式(13)和(14),将序值矩阵 R和V 转化为满意度矩阵A和B;
步骤4根据A和B,构建优化模型式(15);
步骤5根据式(16),将模型转化为单目标优化模型式(17);
步骤6将模型转化为标准的指派问题,并采用Hungarian算法求解该优化模型。
基于双边知识匹配的产品开发任务分配算法的具体流程如图1所示。
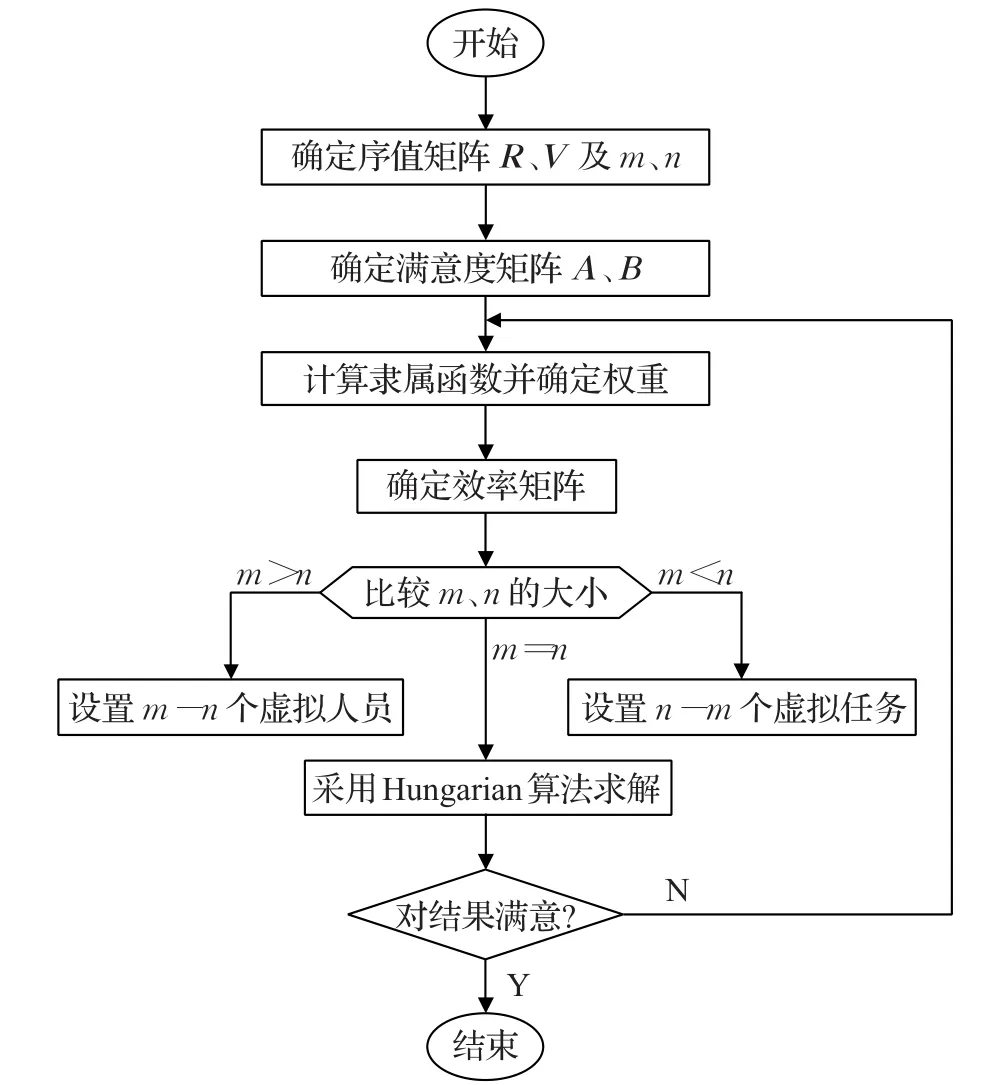
图1 任务分配算法流程图
5 应用实例
5.1 应用实例
国内某公司是一家集研发、设计及制造为一体的高压设备公司,以该公司收到的A型电机设备定制研发设计项目任务为例,对本文所提的基于双边知识匹配的产品开发任务分配方法进行运用。该产品开发任务含5项子任务,分别为T1主轴设计、T2传动链系统设计、T3电气系统设计、T4机舱设计以及T5轮毂设计,即T=(T1,T2,T3,T4,T5)。对应的开发小组共有6名人员P=(P1,P2,…,P6)可承担这5项子任务。公司项目管理小组负责聚合人员和任务双方信息,并对双方进行考察和评价,最终由决策系统将这5项子任务分配给合适的5名人员完成,使双方形成最佳匹配。
根据2.2节内容及企业实际情况,确定显性知识能力测评指标包括人员工作背景与成绩(K1)、常识知识(K2)和专业知识(K3)等3个指标,这些指标可通过决策系统知识库的历史数据获得。隐性知识能力测评指标包括学习能力(C1),工作经验与技能(C2),创新能力(C3),发现、分析和解决问题的能力(C4)以及交流、反馈和重用知识的能力(C5)等5个指标,然后采用基于模糊语言评语集的Delphi法对人员的隐性知识能力进行评价,并以知识库历史数据为依据对人员显性知识能力进行评价,最终获得各项子任务Ti对人员集合P的评价序值向量Ri=(ri1,ri2,…,ri6),其中i=1,2,3,4,5。此外,根据2.3节及历史经验数据,最终确定阈值λ=0.65,将每位人员已完成任务包含的知识项中偏离相似度大于此值的知识项组成一个新的人员知识兴趣集合,然后计算每项开发任务的知识需求包含的知识项集合与每名人员Pj的知识兴趣集合的匹配度,最终获得人员Pj对于开发任务集合T的评价序值向量Vj=(v1j,v2j,…,v5j)T,j=1,2,…,6。由于篇幅限制,具体的计算过程略去,最终人员对任务的序值向量Ri和任务对人员的序值向量Vj如下:

依据Ri和Vj分别建立序值矩阵 R=[rij]5×6和V=[vij]5×6,再根据式(13)和(14),将序值矩阵 R 和V 转化为任务对人员的满意度矩阵A=[αij]5×6和人员对任务的满意度矩阵 B=[βij]5×6,分别如表1和表2所示。其中,θ=1。

表1 任务对人员的满意度矩阵

表2 人员对任务的满意度矩阵
根据表1和表2,可构建多目标优化数学模型式(15),通过Hungarian算法可求出为保证任务和人员双方的公平性,本文取ω1=ω2=0.5。根据式(16),可建立单目标优化模型式(17)。在本例中,任务数量m=5,人员数量n=6,因此可以设置一个虚拟任务。最终的系数矩阵C=[cij]5×6如表3所示。运用Hungarian算法,求解该优化模型,可得双边匹配方案 X*=[xij]5×6,即将T1与P3匹配,T2与P1匹配,T3与P4匹配,T4与P2匹配,T5与P5匹配,P6不完成任何任务。

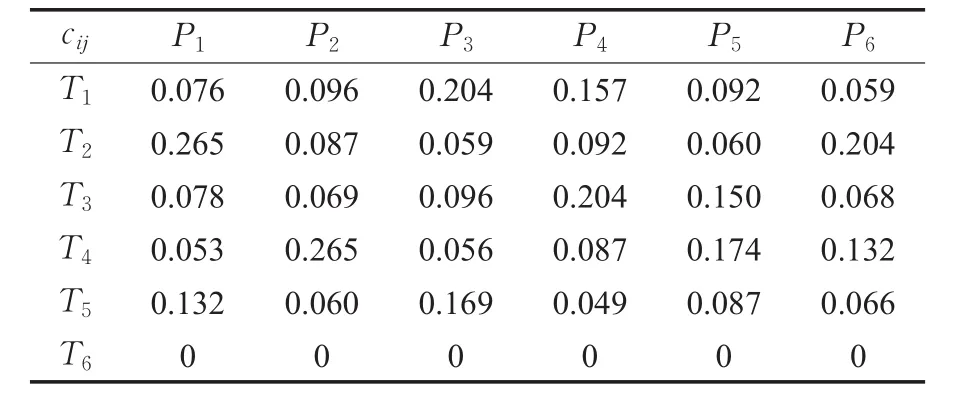
表3 系数矩阵
为分析方便,分别求出不同权重和满意度衰减系数下的任务分配方案,如表4所示。由表4可知,当满意度衰减系数θ分别为0.5、0.8和1.0时,在相同的权重分配方案下最终的任务分配方案相同,而当满意度衰减系数θ取同一个值时,任务分配方案也会随着权重分配方案的变化而变化。因此,可以得出结论:(1)满意度衰减系数的变化不会影响最终的任务分配方案;(2)任务和人员双方的权重系数会影响最终的任务分配方案。
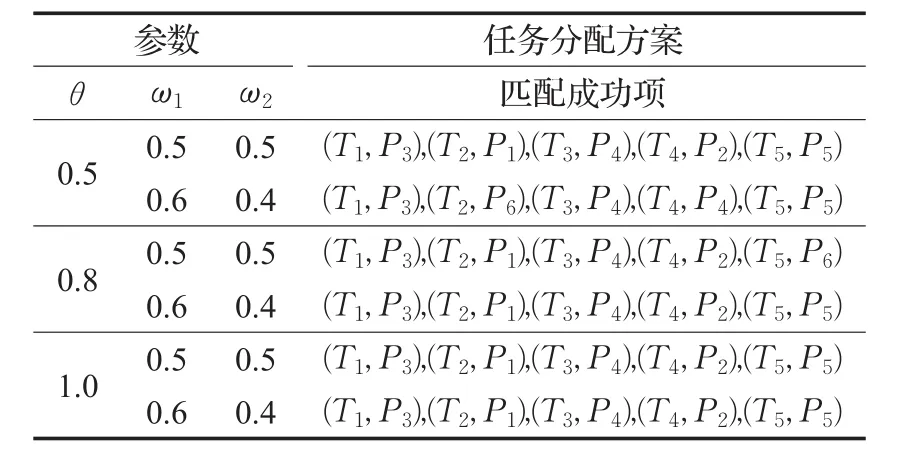
表4 基于满意度衰减系数及权重任务分配方案
5.2 应用实例对比
为了验证本文基于双边知识匹配的产品开发任务分配方法的有效性,将上述实例应用于文献[7]的单边匹配方法中,可得匹配方案 X*=[xij]5×6,即将T1与P4匹配,T2与P1匹配,T3与P5匹配,T4与P2匹配,T5与P3匹配,P6不完成任何任务。
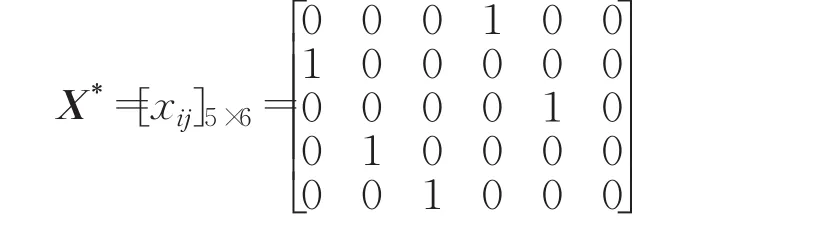
通过实地考察与调研,记录人员对任务的满意度如表5所示。

表5 人员对任务的实际满意度矩阵
该分配方案所对应实际满意度依次为0.20、0.90、0.20、0.90、0.20,其平均满意度为0.48;而本文所提分配方案所对应实际满意度为0.95、0.90、0.95、0.90、0.40,其平均满意度为0.82。对比两种方案,平均满意度提升值为0.34,证明了本文所提方案的有效性。
6 结束语
本文提出了基于双边知识匹配的产品开发任务分配方法,在理论上,阐述了产品开发人员与任务双边匹配的机制,一方面,提出基于显性与隐性的人员知识能力评价机制以实现人员与任务的匹配;另一方面,提出基于知识兴趣的任务知识需求评价机制以实现任务与人员的匹配,为研究产品开发能力提升和效率优化提供了新方向。在实践上,构建了基于双边知识匹配数学模型,为产品开发人员与任务的匹配提供了量化模型。本文在任务分配过程中充分考虑了人员和任务双方的需求,避免了传统任务分配方法中只考虑单边的情形。下一步工作,针对人员知识能力的评价,将人员的知识学习能力作为其中一项评价指标,以体现知识的动态性。

