借助“纠错笔记”整合资源的思考

☉江苏省包场高级中学 张春华

学生对待错误的态度往往会影响其数学学习成绩.教师在平时教学中应善于引导学生将错误视为自己前进的阶梯并认真进行错题的研究，使学生能够在不断挖掘、整合错误资源的过程中分析错因、纠正错误、深挖外延.要求学生做“纠错笔记”是笔者帮助学生纠错的一个重要手段，本文结合笔者在纠错方面的一些具体做法浅谈如何利用“错题”资源帮助学生深化知识的理解.

一、纠正概念理解的偏差

例1 求经过点M（3，6）且在两坐标轴上截距相等的直线方程.

错因分析：（1）截距概念领会不清.

截距：设直线和两坐标轴的交点分别是（a，0）、（0，b），则a即为直线在x轴上的截距，b则为直线在y轴上的截距.截距的值正负皆可，也可为0.截距往往会与距离这一概念产生混淆，需要注意的是距离的值不可能为负数，具体解题时应避免此类错误.

（2）考虑问题不周.

此题应考虑截距为0和不为0这两种情况进行解题，将直线方程设为情况排除在外了，说明解题时还犯了考虑问题不全面的问题.

解：若截距是0，则直线过原点与点M（3，6），直线方程则为y=2x；若截距不是0，则解法与错解相同，直线方程即为x+y-9=0.

反思：此类问题出错一般会包含概念领会不清、问题考虑不周全这两个原因，我们一定要对教材真正展开研究并准确领会概念的内涵，将概念灵活应用于解题中.很多数学问题的解决都会涉及分类讨论的思想，且学习截距这一概念时应知道截距可能存在的情况，因此，解题思考时一定要考虑周全以防止错解和漏解.

二、纠正忽视公式、定理等适用范围的错误

错因分析：基本不等式成立的条件在解题中被忽视导致出错.在时，取“=”.又因为|sinx|≤1，因此这不可能成立，也就是基本不等式中的等号是不成立的，所以不可能是该函数的最小值.

解：因为0＜sin2x≤1，令t=sin2x，则t∈（0，1］，函数y=t+上为单调递减函数，当t=1时，函数有最小值，即sinx=±1时，ymin=4.故函数的最小值是4.

反思：利用基本不等式求函数的最值是普遍且应得到重视的解法，但在具体解题时要注意三个条件的考察：一正、二定、三相等.也就是说，首先要考察函数解析式中各项是否都是正数，然后要考察函数解析式中各项的和或积是否有一个是定值，最后还要考察不等式中等号成立时是否能取得最值.

质疑：若最值问题中需要使用基本不等式两次又该怎么办呢？

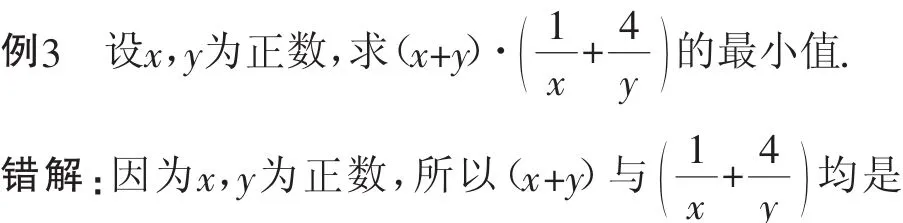
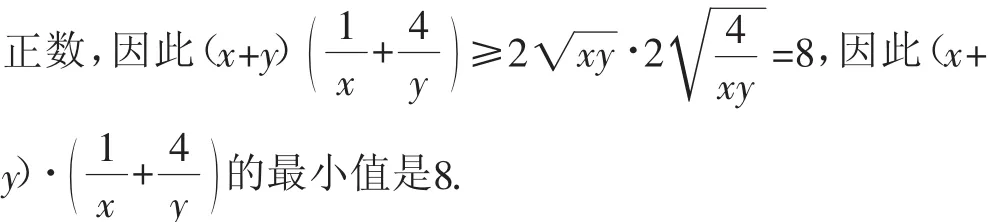
错因分析：此题出错是因为两次使用基本不等式时等号成立的条件不能同时成立而导致的当且仅当x=y时，取“=”；而不等式仅当y=4x时，取“=”.又因为x，y为正数，因此x=y，且y=4x不可能同时成立.

此问题应该怎样解决呢？应该对原式进行重新整理组合并创造一定的条件进行运用.

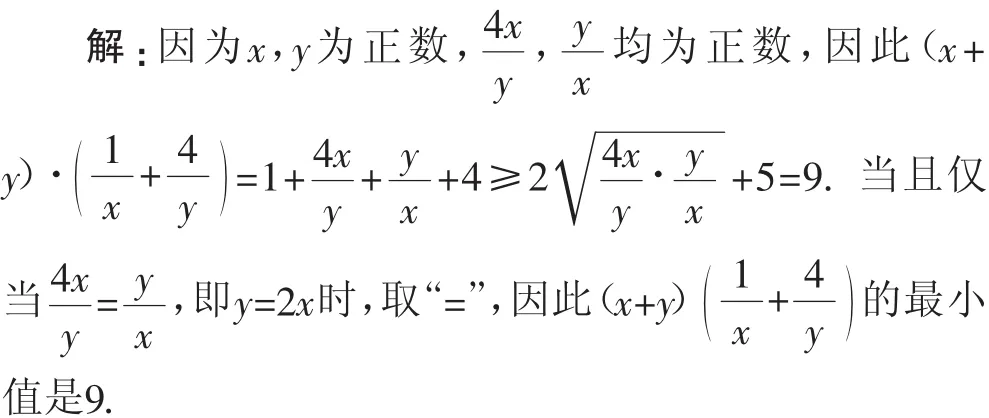
反思：“=”成立的条件是解决此类题目时尤其需要注意的，两次运用基本不等式时，要在两次使用不等式时的条件一致的情况下才能运用.

三、构造知识网络并拓宽思路

解题思路的开阔与否往往能够决定解题能力的高低，而知识网络的建构情况又往往决定着解题思路的开阔程度.如果学习者的大脑中已经形成一个较为完善成熟的知识网络体系，那么，学习者的大脑在面对具体问题时往往能够根据知识内容、思考角度、观察角度等快速进行解题思路与方法的构建，很多不同的解题方案与思路也正是这样形成的，知识网络的实现与解题思路的拓宽是相对统一且相辅相成的.

例4 已知实数a，b，x，y满足a2+b2=1，x2+y2=16，求ax+by的最大值.

错解：因为a2+b2=1，x2+y2=16，所以1+16=a2+b2+x2+y2=

思路1：求函数的最值问题时最容易联想到的便是利用基本不等式，尤其看到题设中“a2+b2=1，x2+y2=16”这一条件，这一想法也就更加坚定了，但直接利用基本不等式求解此题却是行不通的.

（ax+by）2=（ax）2+（by）2+2axby≤（ax）2+（by）2+（bx）2+（ay）2=a2（x2+y2）+b2（x2+y2）=（x2+y2）（a2+b2）=16，因此，|ax+by|≤4，故ax+by的最大值是4.

思路2：因为题设中有“a2+b2=1，x2+y2=16”，由此可联想三角函数满足sin2x+cos2x=1，|sinx|≤1，|cosx|≤1，最后结合三角函数的运算性质及其自身的有界性即可顺利解决本题.

由a2+b2=1，x2+y2=16，可设a=sinα，b=cosα，x=4sinβ，y=4cosβ，则ax+by=4sinαsinβ+4cosαcosβ=4co（sα-β）≤4.

知识网络：sin2α+cos2α=1；

cosαcosβ-sinαsinβ=co（sα+β）；

cosαcosβ+sinαsinβ=co（sα-β）；

sinαcosβ-cosαsinβ=sin（α-β）；

sinαcosβ+cosαsinβ=sin（α+β）；

sin2α=2sinαcosα；

cos2α=cos2α-sin2α=2cos2α-1=1-2sin2α等.

思路3：由ax+by可联想到向量数量积的坐标形式.设m=（a，b），n=（x，y），则ax+by=m·n=|m||n|cos〈m，n〉，|m|=

所以ax+by=m·n=|m||n|cos〈m，n〉=4cos〈m，n〉≤4.

知识网络：m=（a，b），n=（x，y），ax+by⇒ax+by=m·n=|m||n|cos〈m，n〉≤|m||n|.

根据以上三种解题思路可以进行知识网络的构造，即求ax+by的最大值有下述三种方法：①利用基本不等式求解；②利用三角函数求解；③利用向量的数量积求解.

借助“纠错笔记”进行“错题”资源的各种挖掘能使学生在反思错误中不断明晰错因，在整合知识中不断提升自己分析问题、解决问题的能力，使学生保持数学学习的长久热情并获得学习效率的不断提升.W