促进发展，和谐共建——基于学生发展的数学教学实践研究

☉江苏省西亭高级中学 马宇杰

一、问题的提出

维果茨基在二十世纪二三十年代就提出了教育学应以儿童发展的明天作为方向的言论，前苏联教育家赞科夫在他提出的“最近发展区理论”的基础之上也深入剖析了传统教学的弊端，赞科夫提出了以“学生的发展”为本的教学理论.人们随着社会发展的日益加快也越发关心教学与发展.我国教育专家裴娣娜一直持学生发展依赖发展性教学的观点，她认为发展性教学理论与社会要求以及课程标准是能够匹配且相互适应的.

很多数学概念、公式的形成因为发展性教学的实施而变得更为清晰和具体，学生在清晰而具体的认知过程中也更易对学习对象形成深刻的理解.学生在理解教学活动的内部结构与进程的基础上往往更易对知识形成完整的构建，不仅如此，还能在学习的过程中寻得适合自己的学习方法并不断提升自学能力.高中生已经具备了一定的抽象逻辑思维，学生也逐步开始在已有经验的基础上学会理论的概括且逐步走向成熟.本文结合两角和与差的余弦公式进行了发展性教学的思考与探索，发展性教学下对这一内容的研究往往能够提升学生对两角和与差的余弦公式的理解并促进其数学思维发展.

二、教学设计

1.创设情境

师：三角函数的定义是我们已经学过的内容，一些特殊角的三角函数值也是我们同学清晰记得的，如，那么我们是否可得出cos15°=cos（45°-30°）=？大家来猜想一下吧，这一式子的结果会不会等于cos45°-cos30°呢？

生1：不可能，因为cos15°是正的，但cos45°-cos30°是负的，因此不会相等的.

师：说得不错，那么这种猜想不对的话，正确的结果应该是什么呢？

（学生都陷入了思考中）

师：这个结果确实也不是我们同学能力范围内的，不过通过本课的学习，大家应该能够知道了，今天我们就来研究cos（α-β）的值应该怎样确定，看看它和α，β的三角函数值会不会有什么关系.大家可以尝试一些特殊的情况对这一公式的结构形式进行大胆猜想.

由此可见，我们所要讨论的公式形式和cosα，cosβ以及sinα，sinβ应该都有关系，那么它们之间究竟存在着什么样的代数关系呢？

2.学生活动

师：请大家看一下此题并进行解题尝试.

若向量a=（cos75°，sin75°），b=（cos15°，sin15°）.请大家运用数量积的定义与坐标方法分别计算：a·b=|a||b|cosθ及a·b=x1x2+y1y2.请大家对两次计算的结果进行比较并看看能否发现什么？

生2：向量的数量积有两种表达形式，根据这两种不同的表达形式可得cosθ=cos75°cos15°+sin75°sin15°，θ是a，b两个向量的所成角，即θ=75°-15°，因此可得cos（75°-15°）=cos75°cos15°+sin75°sin15°.

师：太棒了，大家有没有从这一特例中获得一点启发并将这一结论进行推广？

同学们面对这一问题纷纷跃跃欲试并展开了热烈的讨论，争取将问题一般化并运用特例进行一般结论的猜想.

3.公式的构建

生3：可以猜想到cos（α-β）=cosαcosβ+sinαsinβ.

师：生3的这个猜想对不对呢？

生4：可以运用特殊值来进行验算，如α=30°，β=60°；α=90°，β=45°；α=240°，β=30°，用这三组特殊值验算可以发现猜想是对的.

师：大家如果觉得该公式是对的，数学的严谨性大家也是都知道的，那么是否能够对其进行一番证明呢？请同学们对上述两式的构成要素与结构特征进行仔细的观察，看看大家是否有什么启发、联想或者发现.

……

生5：从上述特例cos（45°-30°） 以及cos（α-β）=cosαcosβ+sinαsinβ这一式子左右的结构特点可以发现，其右边和向量数量积公式的坐标表示是十分相近的，不仅如此，我们可以联想构造终边与单位圆的交点分别是A（cosα，sinα），B（cosβ，sinβ），结合向量数量积的两种运算方式即可得到以上恒等式.

师：请你将整个证明过程在黑板上板演一下，其他同学在稿纸上完成证明.

证明：如图1，在平面直角坐标系xOy内作单位圆O，以Ox为始边作角α，β，它们的终边与单位圆O的交点分别为A和B，则=（cosα，sinα），=（cosβ，sinβ），=cosαcosβ+sinαsinβ.

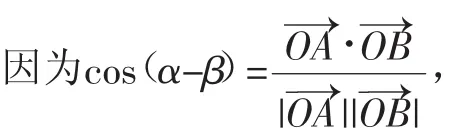
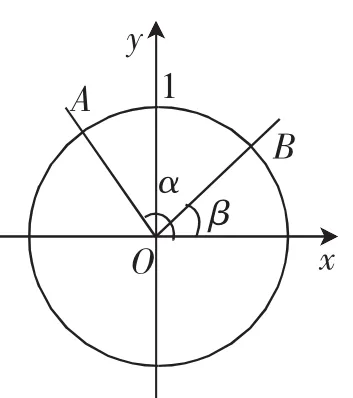
图1

所以cos（α-β）=cosβcosα+sinβsinα（0≤α-β≤π）.

师：生6，生5的解答过程跟你的是否一致？

生6：我漏写了（0≤α-β≤π）.

师：大家觉得这一条件是否一定要注明呢？

生5：我认为是必需的，毕竟两个向量的夹角是［0，π］.

师：生5的回答完全正确，但大家有没有想过这一公式是不是只能在（0≤α-β≤π）这一条件下成立呢？

学生在座位上窃窃私语起来：假如一定需要这一条件，这个公式实际应用的局限性好像很大啊.

①当α-β∈［0，π］时，则α-β=θ，cos（α-β）=cosθ=cosαcosβ+sinαsinβ；

②当α-β∉［0，π］时，则存在k，m∈Z，使得α-β=2kπ+θ或β-α=2mπ+θ.

不管何种情况，都有cos（α-β）=cosθ，即cos（α-β）=cosθ=cosαcosβ+sinαsinβ.

这里需要同学们尤其注意公式结构特点的观察，这能有助于我们同学记忆，同时，公式的逆向运用也是我们需要注意的.

变式：

①cos25°cos20°-cos65°cos70°=______.

②cos58°sin37°+sin122°sin53°=______.

师：大家还有其他方法能够推导出两角差的余弦公式吗？这个问题请大家参考教材中的探究模块并自主完成.

4.例题讲解

教材中的例题讲解略.

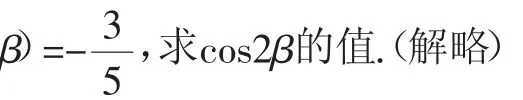
师：角的拆分是此题中我们需要注意的，比如：

（1）已知角2α，β的正余弦值，则2α+β的三角函数值应怎样求出？

（2）已知角α+β，α-β的正余弦值，则2β的三角函数值应怎样求出？

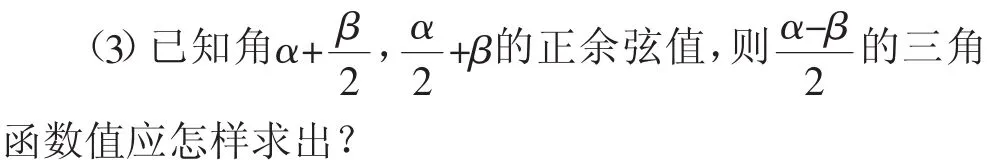
5.课后作业（略）

三、教学评价

高考对于高中整个阶段的教学来说只是一个阶段性的评价，考分虽然能够对学生的学习作出一定的客观反映，但它并不是唯一的衡量指标.以学生发展为本并倡导学生的整体与持续发展是发展性教学理论一直强调的，因此，教师应将学生的思想品德、文化知识、劳动技能、身体素质等多个方面内容均考虑进学生的学习评价中.国家对创新型人才的需求也是对当今教育教学所提出的要求.国际上已经将不会主动探求新知或不会实践应用知识的人归结为文盲，随着国际间的交流增多，知识更新加快，教育教学也必须顺应形势才能使学生能够不断增强应变能力以适应社会环境的变幻莫测.高中学生因为自身视野的局限往往未必能够考虑良多，但教师应该能够认清社会发展的形势，应将学生的认知因素、情感、意志等内容的评价置于学生的综合评价之中，一改过去依赖考分评价学生学习情况的片面性，使学生能够在知识学习、能力达成、情感表现等各个方面均得到客观的评价，使学生能够在不断的实践探索、创新思维中增进知识、情感、价值观等多方面的综合发展.

教师在本课的教学活动中不断引导学生进行探索、猜想、发现与推导，两角差的余弦公式在学生猜想、推导得出的过程中也令学生的运算能力、逻辑推理能力大大提升，学生体验探究乐趣的同时也大大锻炼了数学素质，学生在两角差余弦公式的运用中学会了简单的求值、化简证明并体会到了化归思想的运用，这有助于学生辩证看待问题的良好习惯的养成.

教师的教学艺术如果紧紧局限在传授知识的层面，那必然是狭隘的，更为艺术的是对学生的激励，学生在愉快和谐、自由思考的氛围中往往能够获得更多的思想火花与知识情感.因此，教师在情境创设、探究设计等各个环节都应体现学生的主体地位，使学生能够在浩瀚繁杂的知识中进行关系的探寻、数学思想的挖掘以及知识体系的构建，让学生在教师的启发与引导下学会思考并真正获得数学素质的全面发展.W