基于优化移动均值滤波的频谱降噪分析方法
王李鹏 梁 琪 邹先立 刘 嘉
基于优化移动均值滤波的频谱降噪分析方法
王李鹏 梁 琪 邹先立 刘 嘉
(中国酒泉卫星发射中心,兰州 732750)
电磁环境监测中,背景噪声的抑制和滤除是影响频谱分析的最关键因素之一。本文针对传统的移动均值滤波算法存在的不足作了部分改进,使传统的均值滤波算法得以优化。大量的实验证明,优化后的滤波算法能够更合理地降低噪声对信号的影响,减小信号失真,滤波效果好,灵敏度高。
电磁环境监测;背景噪声;抑制;滤除;移动均值滤波
随着现代网络、通信、电子技术的高速发展,越来越多的无线电信号环绕在人们周围。在民用、商用、航天等各个领域,对无线信号的电磁环境监测凸显出越来越重要的地位。不同时间、不同地点、不同角度监测得到的信号频谱图背景噪声不同,背景噪声影响数据的输入、采集、处理等各个环节以及输出的全过程[1]。因此,背景噪声的提取或抑制一直是频谱分析领域的基本问题,研究如何从嘈杂的噪声信号中提取分离出有用的信号电平具有十分重要的意义。
根据噪声幅值的不同,基本可以分为椒盐噪声和高斯噪声,在电磁环境监测中经常遇到的属于高斯噪声[2-5]。针对高斯噪声,移动均值滤波法是国际上最常用、最基本的滤波方法,算法简单、运算速度快,深受广大学者欢迎。为了达到更高的滤波准确度,提升滤波效果,本文将对现有的移动均值滤波算法进行研究,并改进优化。
1 传统的移动均值滤波算法
假设某一信号频谱分量(),=0, 1, 2, …,-1,包含个非平稳数据,设滤波窗大小为奇数,即取一组长度为的数组,计算平均值
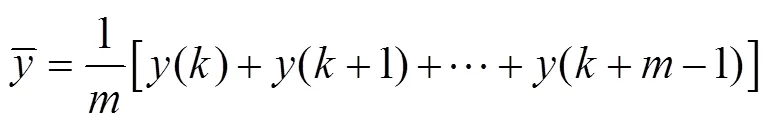
式中,0≤≤-。
特别地,在信号频谱边缘处,所取窗口大小无法使得该信号电平值处于窗口中心位置时,适当减小窗口宽度直至=1。Matlab中移动均值滤波器默认的窗口大小为3,即滤波后的信号电平值为[10-13]:
(1)=(1);
(2)= [(1)+(2) +(3)]/3;
(3)=[(2)+(3)+(4)]/3;
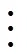
(-1)=[(-2)+(-1)+()]/3;
()=().
2 移动均值滤波的算法优化
不难发现,传统的均值滤波算法对单频点单数值的脉冲信号的削弱效果较为明显,此外,滤波窗口的大小具有不确定性。传统均值滤波算法的滤波窗口通常在整个算法过程中人为地取定值,实际上,在计算窗口内所有频谱信号电平的平均值时,各个信号电平分量模值的影响和贡献是不一样的。若窗口内的电平均值与窗口中心值差异较大,则表明该处存在噪声的可能性较大。
针对上述问题,本文推出了一种确定滤波窗口大小的方法,并在计算窗口内电平均值时引入了另一种求电平均值的方法,即加权平均值法[1]。
加权平均值法既可以求出窗口内信号电平的均值,又顾及了各个信号电平分量模值对窗口内信号电平均值的贡献和影响,加权平均值的定义为
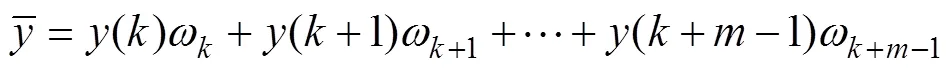
式中,为加权系数,即窗口内某一信号电平模值占整个窗口所有电平模值之和的百分比。
假设个相邻信号电平的方差小于1,则认为该段区间是近似平稳的,窗口大小确定为。反之,则适当减小的取值,直至该段区间近似平稳或的取值减小至1为止。个相邻信号电平的方差为

优化后的移动均值滤波算法流程如图1所示。
3 试验结果与分析
3.1 试验设置及方法
试验装置选用双脊喇叭天线、对数周期天线、低噪声信号放大器及频谱分析仪构成无线电信号监测系统,系统结构如图2所示。在通用频段内,喇叭天线主要接收频率在1GHz以上的信号,对数天线主要接收频率在1GHz以下的信号,通过改变天线的朝向使得各个方位的无线电信号通过频谱分析仪显示出来。

图1 优化的移动均值滤波算法流程图

图2 试验装置结构图
3.2 试验结果及分析
高斯噪声是一个具有零均值的平稳随机过程,但在实际的电磁环境监测中,由于监测环境、天线、线缆、接收机等硬件系统性能的不同,以及监测系统对无线电信号的放大、衰减、滤波、数字化等作用,使得信号频谱图的背景噪声具有不同的纹理特征。
为了进一步检验改进型移动均值滤波算法的优越性和准确性,通过对某一相对稳定开放的环境内无线电信号进行长时间大量的监测,分别用传统的均值滤波算法和优化后的均值滤波算法对监测得到的上百幅频谱图进行降噪分析并统计。结果表明:优化后的均值滤波算法,能够在合理的抑制不同频段不同时间的无线信号背景噪声的同时,更好地保留原始信号真值。本文以某一频段为例,对两种滤波算法的降噪效果具体分析比较。
图3所示为试验过程中频段为930~1000MHz的频谱图,取该频谱图的原始数据,对原始数据分别用两种均值滤波算法进行降噪处理。传统的均值滤波算法滤波窗口分别取=3和=15时,得到的结果分别如图4、图5所示,优化后的滤波结果如图6所示。
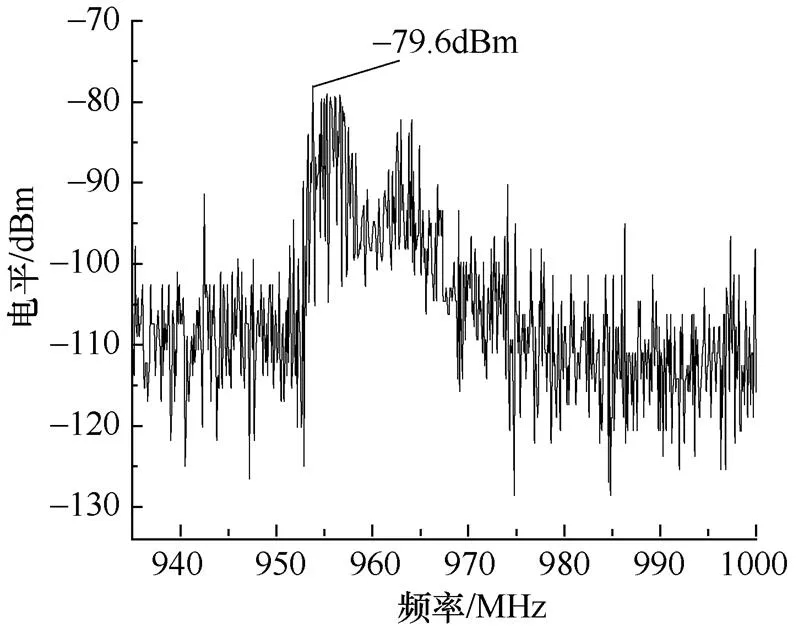
图3 试验频谱图样本

图4 传统均值滤波窗口为3的结果
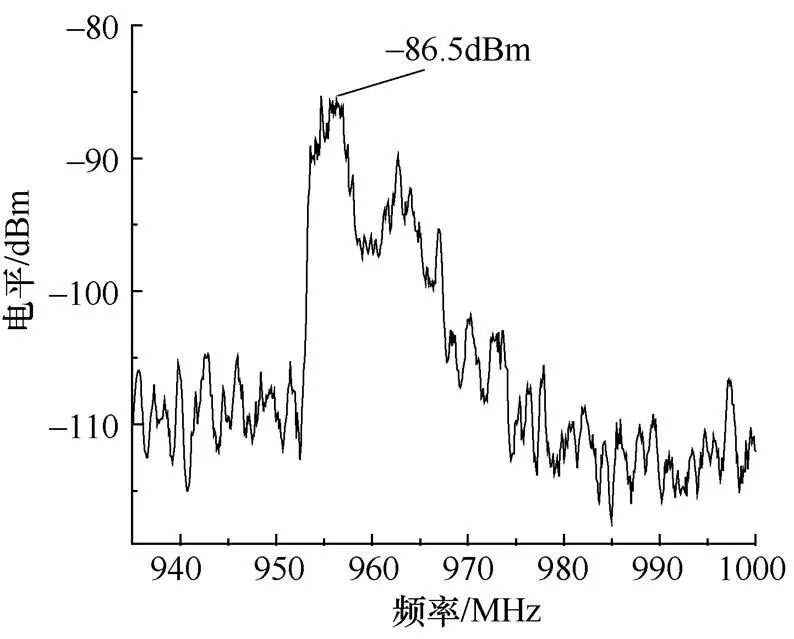
图5 传统均值滤波窗口为15的结果

图6 优化的均值滤波结果
对比图4至图6可知,两种滤波方法均能有效的抑制和滤除部分背景噪声,使得有用信号显现出来,但滤波效果有所不同。
对传统的均值滤波算法而言,当滤波窗口取值较小时,信号平滑度低但灵敏度高,信号峰值与原始数据吻合度较高;当滤波窗口取值较大时,信号平滑度高但灵敏度低,信号峰值与原始数据相比失真较大,难以达到动态平衡。
优化后的均值滤波算法在整个滤波过程中,滤波窗口的大小随着信号电平平稳度的变化实时改变。此外,算法中还考虑了各个信号电平模值分量的影响,噪声抑制效果好,滤波灵敏度高。与传统的均值滤波算法相比,不仅使得有用信号从噪声中清晰地分离出来,而且减小了信号失真,避免了信息元丢失。
4 结论
本文对传统的均值滤波算法进行了优化,通过改进窗口段数据平均值的求法并用限定方差的方法灵活限定滤波窗口的大小,以达到抑制噪声的目的。通过大量的实验表明,优化后的移动均值滤波算法与传统的均值滤波算法相比,能够更合理地降低噪声对信号的影响,减小信号失真,滤波效果好,灵敏度高,对以后的电磁环境监测和频谱信号分析具有非常重要的意义。
[1] 张书豪. 一种改进权重的非局部均值滤波算法[J]. 信息通信, 2017(5): 12-14.
[2] 蔡斌, 刘卫, 郑重, 等. 一种改进的非局部均值去噪算法[J]. 模式识别与人工智能, 2016, 29(1): 1-10.
[3] 郭贝贝, 易三莉, 贺建峰, 等. 改进的非局部均值滤波算法[J]. 计算机工程, 2016, 42(7): 227-231.
[4] 邵琪, 邬延辉, 薛培培. 一种自适应双阈值模糊中值滤波算法的研究[J]. 移动通信, 2015, 39(8): 75-79.
[5] 冯霞, 龚晓峰, 张利丹, 等. 基于纹理特征的背景噪声提取的应用研究[J]. 电子学报, 2009, 37(9): 2092- 2095.
[6] 罗欢. 基于均值滤波器的Fryze三相有功电流检测[J]. 电气技术, 2006, 7(11): 29-31.
[7] 许德志, 汪飞, 阮毅, 等. 并网接口滤波器拓扑结构推演与分析[J]. 电工技术学报, 2015, 30(4): 15-25.
[8] 林天祥, 张宁, 胡军. 基于优化权重的卡尔曼滤波与无偏灰色组合模型的短期负荷预测[J]. 电气技术, 2017, 18(9): 19-23.
[9] 陈亮, 毕天姝, 李劲松, 等. 基于容积卡尔曼滤波的发电机动态状态估计[J]. 中国电机工程学报, 2014, 31(16): 2706-2713.
[10] 朱士虎, 游春霞. 一种改进的均值滤波算法[J]. 计算机应用与软件, 2013, 30(12): 97-99, 116.
[11] 何石, 潘晓璐, 李一民. 一种均值滤波的优化算法[J]. 信息技术, 2012(3): 133-134, 137.
[12] 陈晓威, 董纪清. 有源EMI滤波器研究现状综述[J]. 电气技术, 2017, 18(2): 5-9, 40.
[13] 熊连松, 卓放, 刘小康. 增强型滑动平均滤波算法及其在畸变电网相位同步控制中的应用[J]. 电工技术学报, 2015, 30(21): 13-23.
Spectral denoising method based on modified average filtering algorithm
Wang Lipeng Liang Qi Zou Xianli Liu Jia
(Jiuquan Satellite Launch Center, Lanzhou 732750)
In electromagnetic environment monitoring,the suppression and filtering of Background noise is one of the most important factors affecting spectrum analysis. In this paper, the shortcomings of the traditional mobile average filtering algorithm are partly improved, so that it can be optimized. A large number of experiments prove that the optimized average filtering algorithm can reduce the effects of noise to the signal more reasonably, reduce the signal distortion, and have a better filtering effect and higher sensitivity.
electromagnetic environment monitoring; Background noise; suppression; filtering; mobile average filtering
2018-04-24
王李鹏(1991-),男,山西晋城人,硕士研究生,主要从事电磁兼容方面的研究工作。

