磁化强度的磁感应强度依赖函数在Halbach型永磁体阵列研究中的应用

徐小农 卢定伟 王智河 陈年林 王坤明



磁化强度的磁感应强度依赖函数在Halbach型永磁体阵列研究中的应用

徐小农1卢定伟1王智河1陈年林1王坤明2

（1. 南京大学物理学院固体微结构实验室，南京 210093；2. 南京腾驰电子有限公司，南京 211151）

在Halbach型永磁体阵列磁场和磁化强度分布研究中，涉及永磁材料内部磁化强度()、磁场强度()和磁感应强度()三者的相互关系函数()、()和()。本文介绍了这些函数的典型实验特征，说明为计算获得永磁体阵列磁体内部自洽的磁场和磁化强度矢量分布，必须使用()函数。强场永磁体阵列材料内部的磁场和磁化强度矢量分布无法直接被进行实验测量，不恰当地使用()和()函数易导致不符合实际情况的磁场和磁化强度分布状态预测。

Halbach型永磁体阵列；磁感应强度；磁化强度与磁场自洽分布

永磁体阵列是实现单侧增强磁场的有效手段[1]，在电气技术领域有极为广泛的应用[2-9]。在一定理想条件近似下，永磁体阵列在磁体内外磁场分布的解析解[7-15]，在一定近似条件下更接近实际永磁体阵列磁体内外磁场分布的数值解[16-18]，有助于理解永磁体阵列单侧磁场的产生和增强原理，以及永磁体阵列构成磁体材料内部在强自场作用下的局部退磁甚至磁化强度方向翻转的机制。至今材料内部的实际磁化强度分布无法由实验直接观测，近年来不断有针对各种用途永磁体阵列的研究新结果报道，然而涉及永磁体阵列材料内部一些基本的物理现象，如退磁等问题仍然存在一些不完全一致的分析。

在涉及实际永磁体阵列材料的磁化状态以及产生磁场空间分布的数值计算中，需要用到磁体阵列构成材料（超高矫顽力硬磁，超高磁能积硬磁）各向异性的磁滞回线。在推导磁体内外磁场分布的解析表达式过程中，也需要用到理想化的有关磁化强度（）、磁感应强度（）和磁场强度（）三者的相互关系。电磁学中磁感应强度矢量是代表磁场的基本物理量，而磁场强度矢量是为了描述磁场方便引入的辅助物理量，在电气工程技术领域描述磁性材料特征时，常用()磁滞回线来表征永磁材料磁化强度对外加磁场强度的响应。本文介绍永磁材料的不同方向的磁特征函数()，()和()是如何获得的；说明在永磁体阵列材料内部磁感应强度和磁化强度分布分析中，使用()函数存在的局限性以及永磁体阵列磁化状态和磁场分布若干基本物理问题存在争议的原因；强调要用()函数才能获得的材料内部自洽的磁感应强度和磁化强度分布，从而正确认识实际发生在永磁体阵列构成材料内部的、偏离材料初始磁化状态分布的复杂磁化现象。

1 永磁体材料的磁化特征函数

1.1 磁化强度的磁场强度依赖函数M(H)

硬磁材料具有明显的各向异性，图1给出了钕铁硼永磁材料样品磁化强度对于磁场强度的实验磁化曲线()。均匀磁化的椭球状样品内部的磁场强度应当修正为

=0（1）

式中，为椭球样品的形状退磁因子；0为外加磁场强度。如图1中的两线[0||(0||),0^(0^)]是通过0(00)测量，经过式（1）退磁修正后，等价于无退磁效应（=0）样品在平行与垂直磁化主轴两个方向上的磁滞回线。

图1 一种钕铁硼永磁材料样品在平行与垂直易磁化轴方向m0M||(m0H||), m0M^(m0H^), m0M||(B||), m0M^(B^)磁滞回线

式中，和都很大时（≥10，1），0≈1。这说明了有强退磁形状的样品，即使真实的磁化率达到102-4量级，在(0)图中起始磁化曲线的斜率0也成为了1。

1.2 磁化强度的磁感应依赖函数M(B)

获得()函数后，利用在三维空间成立的矢量表达式

=0(+) （3）

再分别作平行与垂直易磁化轴两个方向上磁化强度和磁感应强度的叠加，进而获得了0()函数如图1中的0||(||)和0^(^)回线。

考虑()图中磁化初始部分=，利用式（3）得到=0(1+)，0()图中磁化初始部分的斜 率为

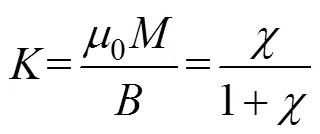
当很大时，=1，因此图1中()回线中几乎垂直向上的起始磁化线，变成()函数中约45°的倾角。

注意图1中易磁化轴方向||(||)的回退曲线与横轴相交位置处的斜率几乎为无穷大，也就是说在=-c磁化强度矢量发生翻转之处，磁化强度存在一定的不确定性，磁化强度并不是磁场强度的单值函数。易磁化轴方向()的回退曲线与横轴相交的位置直线斜率为1，因此磁化强度是磁感应强度的单值函数，在数值计算中使用()函数，就避免了使用()函数在-c处遇到的不确定性。

1.3 磁感应强度的磁化强度依赖函数B(H)

图2是由图1演变过来，在平行与垂直易磁化轴的两个方向上的硬磁材料样品的||(||)，^(^)回线。其中第一、二象限回退曲线在零场附近的线性较好的部分，在易磁化轴方向可以近似表达为

||=0(r||||+R) （5）

式中，r||和0R是拟合常数，分别等于零场附近||(0||)回退曲线被看成直线时的斜率和在轴上的截距。

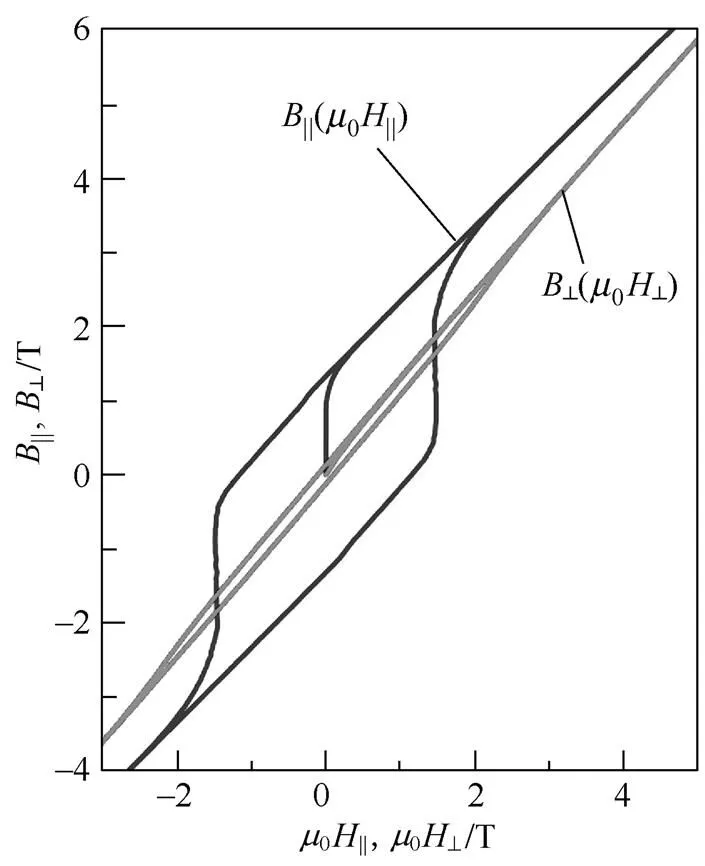
图2 一种钕铁硼永磁材料样品样品在平行与垂直易磁化轴方向B||(H||), B^(H^)回线

垂直于易磁化轴方向的^(^)可以近似表达为

^=0r^^（6）

Halbach最初提出类似于式（5）的()关系时[1]，是将r看成是拟合常数，后来有学者定义式（5）中的r为回退磁导率[8-11]。要注意这里的r不符合传统磁导率的物理定义，因为回退磁化曲线M(H)上各点的磁化强度M，不是由对应的磁场强度H激发并且维持的。回退()曲线上隐含的磁化强度，磁体制造工艺上是由脉冲强磁场饱和充磁获得，磁化强度M能保留依靠了永磁材料内部的磁通钉扎，与对应的磁场强度H关联度不是太大。

实际的硬磁材料拟合常数通常r||¹r^，在其他与易磁化轴不同交角方向上r也有不同的值。有学者因为由式（5）、式（6）代表的()关系在平行与垂直易磁化轴的两个不同方向上，回退曲线r||和r^值很接近，就认为材料是各向同性的[11-13]。实际上式（5）用于描述同一硬磁材料相对于磁化主轴不同方向的()关系，参数r即使在相对磁化主轴的不同外场方向很接近，参数R仍会变化很大。拟合参数r本来就不符合磁导率的严格物理定义，与材料真实的各向异性并无太大的关联，即使r||=r^，也完全不能代表各向同性。图2所示的钕铁硼永磁材料样品()回线，尽管r||与r^接近，对应图1中0(0)起始磁导率和剩余磁化强度的数值，沿着易化轴方向与沿着垂直易化轴方向之比，都超过了5倍，磁各向异性非常显著。

2 磁化强度的磁感应强度依赖函数M(B)在永磁体阵列磁场和磁化强度自洽计算的应用

在永磁体阵列情形，磁场强度是由磁体提供的自场。考虑如图3所示硬磁材料理想磁滞回线0(0)和0()，在＜-c之前的=-c，磁化强度从+R变化到-R，=-c称为磁极性转变的临界磁场强度，在临界磁场上材料的磁化强度值需用0()函数自洽计算获得。在图3所示的0(0)回线中，设置了参数R＞c，以展示单一磁块在自场作用下进入退磁临界态=-c的情形。

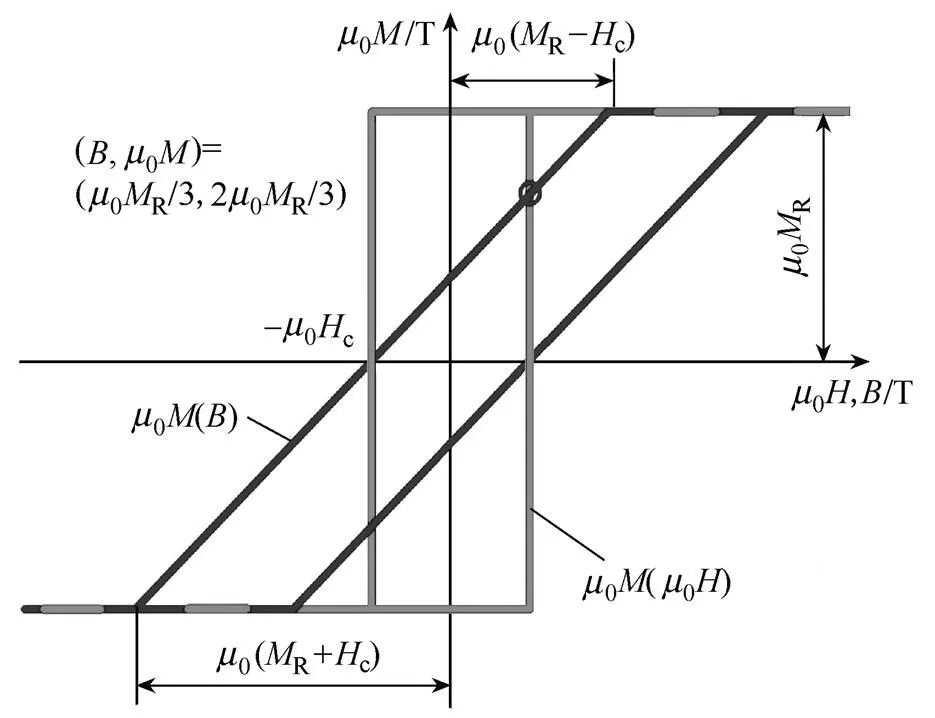
图3 永磁材料的理想m0M(m0H)和m0M(B)回线（为方便说明相关问题，此处设定参量MR＞Hc=MR/3）

下面以一个均匀磁化的旋转椭球（半轴长度分别为,和,=，磁化主轴平行轴）为例，介绍永磁椭球进入转变临界态后，如何获得自洽的磁化强度和磁感应强度一组数值的思路。这是理解如何获得永磁体阵列内部全自洽的磁化强度和磁感应强度矢量分布计算方法的基础。

图3所示的0(0)回线给出=0时，退磁效应可以被忽略的磁椭球的磁化强度=R。如果磁椭球有退磁效应，并且退磁场可以达到或者超过材料的磁矫顽力，即-c，粗略地结合0(0)回线判断，就有可能得出磁化强度极性会翻转的结论。然而，单一永磁椭球在自场作用下磁极性自动翻转，这是违背物理学常识的，实际情形在自场作用下磁化强度会退化但是不会翻转，在0()磁滞回线的回退分支上可以找出自洽的工作点（＞0，0＞0）。

现在假设剩余磁化强度为与矫顽力的关系为

R=c（7）

式中，为常数，＞1时R＞c。如椭球的退磁因子为，那么在外加磁场不存在（0=0）时球内的磁场强度全部来源于自场，磁化强度为R的椭球，在球内产生的均匀磁场强度可以由式（1）和式（7）得到为

==-R=-c（8）

如果＞1，那么＜-c，退磁必定会发生。

在图3所示0()回线给出磁极性转变过程的磁感应强度变化范围是-m0(R+c)＜＜0(R-c)；退磁发生的条件是=0(+R)=0(-R+R)＜0(R-c)，即R＞c。在0()回线上对应磁化强度从+R到-R转变的临界态上

0=0c+（9）

同时，

由上列两式求出一组自洽的(,0)值为

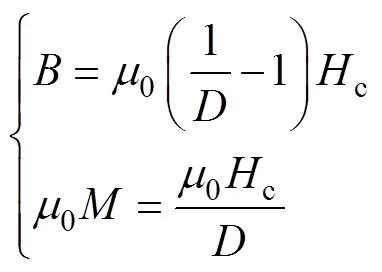
＞1情形在自场作用下，初始饱和磁化的椭球磁化强度值从R自发退化至=c/。利用式（7）可得c＜=R/＜R。假设相关参数如图3所示为=3,=1/2,3/2＞1，则式（11）给出退磁因子=1/2的永磁扁椭球（=＜＝在自场作用下，自洽的磁感应强度和磁化强度工作点位于图3第一象限0()中回线上的小圆圈处。此处(,0)=(0c, 20c)=(0R/3, 20R/3)，对应0(0)回线上的临界磁场强度值=/0-=-(1/3)R=-c。

上述具有图3磁滞回线特征的永磁椭球，在自身磁场作用下磁化强度退化的例子说明，非自洽物理模型下给出的磁场强度值＜-c，并不是一定能导致磁化强度翻转。磁化强度翻转发生在0()回线的=-m0c处。从图3可以看出，=-c表明磁化强度可能退化，＜-c则意味着磁化强度彻底翻转达到反向饱和。达到反向磁饱和，需要的磁感应强度值＜-m0(Rc)，也就是||＞0(Rc)，这是单个永磁椭球自身无法提供的反向磁场。

以上举例说明了对于一个永磁体体元，如何在已知0()函数的基础上获得自洽的磁化强度与磁感应强度。在永磁体阵列情形，要考虑到所有计算磁元之间的相互作用，磁元磁化强度对磁感应强度场响应存在的各向异性，磁化强度饱和，磁化强度转向等因素，利用||(||)和^(^)函数，在采取一定近似的条件下，在永磁体阵列磁体材料内部和外部获得全自洽的磁化强度和磁感应强度分布[16-18]。

2.1 乳腺叶状肿瘤良恶性病理表现 纳入研究107例患者的107个病灶其中良性乳腺叶状肿瘤45个，交界性乳腺叶状肿瘤33个，恶性乳腺叶状肿瘤29个。其中，良性病灶出现膨胀性形状，且间质细胞较为疏松的排列，具有明显的核分裂象(每10个高倍视野下0～4个核分裂象)，但并无出血坏死的病理表象；交界性乳腺叶状肿瘤呈现明显的浸润性生长，且间质细胞生长过度，具有明显的核分裂象(每10个高倍视野下5～9个核分裂象)，可见少量出血坏死现象；恶性乳腺叶状肿瘤间质细胞排列紧密，但胞质内明确可见空泡，且导管稀少，每10个高倍视野下10个核分裂象，可见大片出血和坏死。

3 结果和讨论

3.1 永磁体阵列材料内部磁感应强度，磁场强度和磁化强度三者的基本关系

一些有关永磁体阵列磁场分布的解析解的研究论文[10-11]，将在易磁化轴一维方向成立的式（5）推广到三维矢量空间的等式

=0(r+R) （12）

式中，R代表剩余磁化强度矢量的三维空间分布，而后由已知的R空间分布，通过求出矢量磁势或标量磁势，导出磁感应强度矢量分布或者磁化强度的矢量分布。我们认为将易磁化轴方向上磁场强度和磁感应强度两者关系的式（5），推广成为二维或三维矢量形式的式（12），其合理性存疑。式（5）代表在易磁化轴方向上，磁场强度与磁感应强度两个变量，在一定磁化强度变化范围内的依赖关系，R的地位只是一个拟合常数，在数值上等于剩余磁化强度R=(=0)。永磁体材料内部磁感应强度，磁场强度和磁化强度三者基本矢量关系只能是式（3）。

式（5）中隐含了一个对场敏感的磁化强度模型，由式（5）和式（3）消去磁感应强度得到磁化强度，磁场强度和剩余磁化强度三者矢量关系为

||=(r||-1)||+R（13）

对照图1可见，在易磁化轴方向式（13）在＞-c大致成立，在＜-c实验||(||)关系完全偏离式（8）表达的线性。文献[11]在式（12）的基础之上求解矢量磁势的方法，给出了理想Halbach圆柱型阵列材料内外磁场分布r≥1的解析解，并且否定了文献[10]给出的磁场解析解。利用复变函数直接积分的方法，导出的理想Halbach圆柱型阵列磁体内外磁感应强度分布解析解[15]，与文献[11]中的磁场解析表达式在（r=1）时完全一致，这也进一步证实了文献[11]作者的判断是正确的，文献[10]给出的磁场分布解析解有误。

文献[10-11]采用物理模型本身是不自洽或者是有矛盾的。在推导磁化强度对磁场敏感的情形下永磁体阵列磁场分布解析解的过程中，作者一方面引入常数r＞1表明磁化强度的幅值是对外加磁场敏感的，另一方面在推演过程中使用了||=R的关系，用式（12）中=0时的剩余磁化强度矢量分布R导出同式中磁场强度分布，并未进一步考虑式（13）所示磁化强度随外场的改变，也就是在实际推演过程中，最终又忽略了磁化强度对外加磁场敏感性。

文献[11]在r＞1情形，即磁化强度对磁场强度敏感的假设下，以式（12）为基本函数导出了的双极柱形永磁体阵列空腔内部磁场的解析表达式，始终代表一个与r值有关，大小和方向都恒定的均匀磁场。而实验测量或者依据实验磁化回线()自洽计算出的双极Halbach永磁体阵列空腔内的磁感应强度分布，是有一定变化规律的非均匀场[16]，所以在式（12）基础之上导出的空腔内磁感应强度的解析表达式，在定性上并不符合Halbach永磁体阵列磁场分布的实验变化趋势。磁化强度对磁场敏感的永磁材料（r＞1，或者|¹常数R）的永磁体阵列内外磁感应强度的分布解析表达式，至今依然是一个尚未解决的挑战性问题。

3.2 在永磁体阵列磁场的分析和计算中该使用M(H)函数还是M(B)函数？

文献[13]讨论了磁块局部区域的磁极性在永磁体阵列自身强自场作用下翻转的可能性。该文依据永磁材料的磁化曲线M(H)（如图1和图3所示），在反向磁场强度H小于矫顽力场c时（H＜-c）磁化强度转向，得出Halbach中空柱形永磁体阵列南北外侧两极处的局部材料磁极性，在材料磁参量值c＜R条件下会翻转的结论。这里需要指出，得出这个翻转结论所依据的数值结果，并不符合永磁体阵列磁体内部磁化强度矢量和磁场强度矢量的自洽分布。

＜-m0c（14）

分别用复变函数积分导出的理想中空圆柱型永磁体阵列磁体内外磁感应强度的解析分布表达式，用求解泊松方程方法导出理想中空球形永磁体阵列磁体内外磁感应强度的解析分布表达式，进而依据理想永磁体阵列磁感应强度在材料内部解析分布，建立起解析的退磁函数[14-15]。用实验()关系自洽数值计算获得的实际永磁体阵列材料内部的磁化状态分布[16-18]，都不支持文献[13]提出的Halbach中空双极永磁体阵列外侧南北两极处的磁块局部磁化强度方向、在材料磁参量值c＜R条件下会翻转的结论。

3.3 软铁在永磁体阵列产生的磁场中是容易被饱和磁化的吗？

图1中的0||(0||)是包含了被测量硬磁材料样品自身对磁场强度的贡献以后的磁化曲线0||(0||)。注意起始磁化曲线起始部分几乎是垂直向上的，在0||值达到约0.2T时就获得磁饱和，这说明无退磁效应的内置磁化主轴的块状硬磁，在顺着易磁化轴的方向很容易被饱和磁化；而软磁材料的起始磁化曲线往往比硬磁材料更接近垂直，通常起始磁化率＞102。然而，若认为依靠永磁体或者永磁体阵列产生的静磁场，大块的软磁轻易会被饱和磁化，则是不符合实际情况的。式（2）表明即使是极其容易被磁化的软磁材料，若有比较强的样品形状退磁效应（¹0），则在(0)图中的起始磁化曲线的倾角也会接近45°而不是90°。有强退磁效应的样品，只有在外磁场00基本达到饱和磁化强度值0R的时候，才能被饱和磁化[17-18]。

永磁体阵列任一体元的磁化强度，应该看作是当地磁感应强度的函数，需计及磁元自身的贡献。磁感应强度矢量和磁化强度矢量自洽数值计算的结果表明：在强场永磁体阵列内部磁化强度达到饱和的区域，适度地用软铁替代部分硬磁，圆柱体阵列空腔内部的总体磁通量和磁场均匀度都可能得到改善；但是替代部分硬磁材料的大块软磁，并非轻易达到饱和磁化状态。软铁难以饱和的原因可以从图1所示0()回线的特征以及式（4）看出，软磁材料的起始磁化线的斜率≤1，而软磁材料的饱和磁化强度，通常会远高于硬磁材料的饱和磁化强度。软磁材料替代硬磁材料后主要起到汇聚磁通量到空腔的作用，流经空腔磁隙内的磁通量会增加的同时，永磁体阵列整体磁路中的总磁通量反而会减少[18]。

4 结论

在强场永磁体阵列磁体材料内部，用非自洽方法获得的磁化强度和磁场分布的分析或计算结果，往往与实际情形相差甚远，也很可能导致物理预测情形上的误判。磁性材料磁化强度矢量对外加磁场强度矢量的响应与磁元的几何形状相关，磁化强度的磁场强度依赖函数()难以直接用于涉及强场永磁体阵列材料内部磁化强度和磁场相互作用的自洽分析。相对于磁场强度矢量，磁感应强度矢量为更加基本且能与材料单一磁化状态相关联的物理量。磁化强度的磁感应强度依赖函数()，适用于强场Halbach永磁体阵列关于磁场和磁化强度的自洽分析与计算，研究永磁体阵列产生磁场对材料内部原有磁化状态的改变，如在强自场作用下的局部退磁、磁饱和、磁化强度矢量翻转等复杂的磁化现象。

[1] K. Halbach. Design of permanent multipole mangnets with oriented rare earth cobalt material[J]. Nuclear Instruments and Methods, 1980, 169: 1-10.

[2] J. M. D. Coey. Permanent magnet applications[J]. Journal of Magnetism and Magnetic Materials, 2002, 248: 441-456.

[3] 罗阳. 全球NdFeB磁体产业的变化与发展[J]. 电气技术, 2008, 9(6): 5-11.

[4] 张一鸣, 乔德治, 高俊侠. Halbach阵列永磁体的研究现状与应用[J]. 分析仪器, 2010(2): 5-10.

[5] 宋玉晶, 张鸣, 朱煜, 等. 基于伪周期的Halbach永磁阵列三维磁场端部效应建模研究[J]. 电工技术学报, 2015, 30(12): 162-170.

[6] 罗辞勇, 李竹田, 沈启平. 异形永磁体圆柱型直线电机的优化设计[J]. 电工技术学报, 2017, 32(17): 127-134.

[7] 罗玲, 薛利昆, 吴先宇, 等. Halbach永磁阵列无刷直流电机转矩的解析计算和分析[J]. 电工技术学报, 2017, 32(16): 124-135.

[8] 宋玉晶, 张鸣, 朱煜. Halbach永磁阵列磁场解析求解及推力建模[J]. 电工技术学报, 2014, 29(11): 61-67.

[9] 寇宝泉, 曹海川, 李伟力, 等. 新型双层Halbach永磁阵列的解析分析[J]. 电工技术学报, 2015, 30(10): 68-76.

[10] Xia Z P, Zhu Z Q, Howe D. Analytical magnetic field analysis of Halbach magnetized permanent magnet machines[J]. IEEE Transactions on Magnetics, 2004, 40: 1864-1872.

[11] Bjørk R, Smith A, Bahl C R H. Analysis of the magnetic field, force, and torque for two-dimensional Halbach cylinders[J]. Journal of Magnetism and Magnetic Materials, 2010, 322: 133-141.

[12] Bjørk R, Smith A, Bahl C R H. The efficiency and the demagnetization field of a general Halbach cylinder[J]. Journal of Magnetism and Magnetic Materials, 2015, 384: 128-132.

[13] Insinga A R, Bahl C R H, Bjørk R, et al. Permanence of Halbach magnet arrays with finite coercivity[J]. Journal of Magnetism and Magnetic Materials, 2016, 407: 369-376.

[14] Xu Xiaonong, Lu Dingwei, Xu Xibin, et al. Analytic solution of magnetic induction distribution of ideal hollow spherical field sources[J]. Journal of Mag- netism and Magnetic Materials, 2017, 443: 397-403.

[15] Xu Xiaonong, Lu Dingwei, Xu Xibin, et al. Analytic solution of field distribution and demagnetization function of ideal hollow cylindrical field source[J]. AIP Advances, 2017, 7: 095203.

[16] Xu X N, Lu D W, Yuan G Q, et al. Self-modification of the remanence distribution of a hollow cylindrical permanent magnet array[J]. Journal of Applied Physics, 2006, 100: 043906.

[17] Xu X N, Lu D W, Xu X B, et al. Simulations of remanence and field distributions of permanent magnet array with rectangular cavity[J]. Journal of Applied Physics, 2008, 104: 043919.

[18] Xu Xiaonong, Lu Dingwei, Xu Xibin, et al. Optimizing the field distribution of a Halbach type permanent magnet cylinder using the soft iron and superhard magnet[J]. Journal of Magnetism and Magnetic Materials, 2018, 445: 77-83.

[19] 刘亚丕. 高性能永磁材料磁性测量若干问题探讨及测量技术进展[J]. 电气技术, 2006, 7(9): 9-16.

[20] 赵凯华, 陈熙谋. 电磁学[M]. 2版. 北京: 高等教育出版社, 1985.

Applications of the magnetic induction strength dependent magnetization function in the study of Halbach type permanent magnet array

Xu Xiaonong1Lu Dingwei1Wang Zhihe1Chen Nianlin1Wang Kunming2

(1. Physics College of Nanjing University, National Laboratory of Solid State Microstructures, Nanjing 210093;2. Nanjing Tengchi Electronics Corporation Limited, Nanjing 211151)

In the study of magnetic field and magnetization distribution generated by Halbach permanent magnet array, the relationship functions(),() and() among magnetization (), magnetic field strength () and magnetic induction () are involved. Here the experimental characteristics of these functions are introduced, and it is illustrated that() function should be used in the calculation for obtaining the self consistent magnetization and field distributions inside the permanent magnet array. At the material interior of permanent magnet array, the sophisticated vectorial distributions of field and magnetization may not be experimentally measured, inappropriate use of() and() functions possibly results in the untrue predication of magnetic field and magnetization distributions under the intense self field.

Halbach permanent magnet array; magnetic induction; self-consistent distribution of magnetic field and magnetization

2018-04-23

徐小农（1962-），男，博士，教授，研究方向为磁性材料应用等。

国家自然科学基金（50577030）