两类母线电压谐波责任划分模型的仿真比较
安海清 岳 娜 邢宇欣
两类母线电压谐波责任划分模型的仿真比较
安海清 岳 娜 邢宇欣
(国网冀北电力有限公司检修分公司,北京 102488)
母线电压谐波责任定量划分模型主要分为两类:①为划分单个公共连接点处某个受关注谐波源以及电网侧谐波责任的单点等值模型;②为划分多个谐波源在远端特定母线处产生的谐波污染责任的多点等值模型。首先,从理论上对两类谐波电压责任划分模型的特点及其适用场合进行详细的分析比较;其次,通过对IEEE 14节点标准测试系统进行仿真算例验证。仿真结果表明,单点等值模型适合划分系统背景谐波电压波动较小情况下的谐波污染责任。而当系统中所有主要谐波源情况已知时,多点等值模型可以避免单点等值模型因背景谐波电压剧烈波动带来的谐波阻抗估计误差偏大的缺点,进而更准确地划分每个谐波源在关注母线处产生的谐波电压责任。
电能质量;谐波电压责任;谐波阻抗;背景谐波电压;等值模型
目前,国内外针对电力系统谐波责任方面的研究,基本上都是围绕谐波发射水平[1]、谐波电流责任[2]以及谐波电压责任[3]这3个衡量指标进行,并且都是基于公共连接点处采样的谐波电流和谐波电压数据进行谐波责任划分[4]。这些衡量指标并没有严格的优劣之分,不同的情况和侧重点可以选择不同的指标。其中,谐波电压责任作为衡量谐波源污染程度最常用的方法,主要是因为电压质量是体现电网电能质量的主要方面[5],不管是用户还是供电方,更关注的都是合格的电压,因此,在工程实际中,通常用谐波电压参数量化谐波污染责任[6-7]。
根据系统中谐波源具体位置以及数量等情况,可以将谐波电压责任划分模型分为两大类:①在所有主要谐波源的位置、数量未知情况下,单个公共连接点处某个已知的受关注谐波源和系统侧其余未知谐波源之间的谐波电压责任划分[8],在这里称为单点等值模型。这类模型将未知的非关注谐波源等效为系统侧谐波源,其产生的谐波电压称为系统背景谐波电压,此类模型主要用来确定用户侧和系统侧哪一方对谐波电压污染占主导作用;②系统中主要谐波源已知情况下,多个已知的主要谐波源在某条或者某几条受关注的母线处产生的谐波电压责任划分[9-10],在这里称为多点等值模型。这类模型可以对所有受关注的主要谐波源在特定母线处的谐波责任进行准确区分。
不论是单点等值还是多点等值模型划分母线电压谐波责任,其核心都是估计系统等效谐波阻 抗[11-13]。但是两类模型在估计系统等效谐波阻抗时需要考虑的问题又各有不同。对于单点等值模型,由于只掌握单个公共连接点处某个已知的谐波源负荷情况,系统中其余主要谐波源情况未知,这导致系统背景谐波电压大小以及波动情况无从得知,因此在估计系统谐波阻抗时,需要考虑背景谐波的存在,这可能会影响系统谐波阻抗的估计结果的准确性。此外,系统背景谐波不易被估计准确,这又导致了在划分谐波电压责任时,误差进一步增大。为了解决背景谐波波动影响系统谐波阻抗估计准确度的问题,文献[14]提出了不同的方法进行数据筛选,利用筛选后的数据计算谐波阻抗,但是仍然不能避免线性回归模型本身的系统性误差。文献[15]的作者提出了邻域多点测量的方法,将波动的背景谐波电压划分为不变和可变的2部分,从而降低背景谐波电压的波动性对系统谐波阻抗估计结果的影响。工程上通常用波动量法估计系统谐波阻抗,但是它是基于用户侧谐波波动占主导的情况,虽然有方法对其进行了改进,如主导波动量法[16]、阻抗归一化方法[17],但是这些方法仍然是为了迎合波动量法,因此存在一定的局限性。
对于第2类多谐波源在远端特定母线处产生的谐波污染责任定量划分的多点等值模型,是建立在系统中所有主要谐波源已知的前提下,目前有多种谐波源识别与定位方法[18]。多点等值模型考虑到了系统中所有主要谐波源,相比仅区分系统和用户2侧的谐波责任单点等值模型,可以不用考虑背景谐波电压波动的情况,这很好地弥补了单点等值模型的不足。但是,该模型需要对多个谐波源负荷产生的谐波电流及其所在母线谐波电压进行采集,此时需要考虑到采集的谐波电流之间可能会存在较强的相关性以及数据异常等问题,导致传统最小二乘多元回归方法估计的系统谐波阻抗误差会明显增大。虽然目前有多种多元稳健回归方法解决了异常数据点带来的问题[10],但是仍然无法很好地解决数据存在较强线性相关性时系统谐波阻抗估计不准确的 问题。
本文对两类母线电压谐波责任划分模型做了详细分析并进行了比较,最后通过仿真实验进行对比分析,说明了两类方法各自的优缺点及适用情形。单点等值模型适合背景谐波电压波动不大的场合,而多点等值模型更适合划分系统主要谐波源数量有限且已知的情况。
1 两类母线电压谐波责任划分模型
1.1 单点等值模型
图1所示为单条母线X处接入谐波源负荷。关注母线X的一侧为系统侧,另一侧为用户侧,接入了2个谐波源负荷Load1和Load2。其中Load1表示受关注的谐波源负荷,要求计算Load1在母线X处产生的谐波电压责任。Load2模拟系统侧所有未知的非关注谐波源,其产生的谐波电压为系统背景谐波电压。
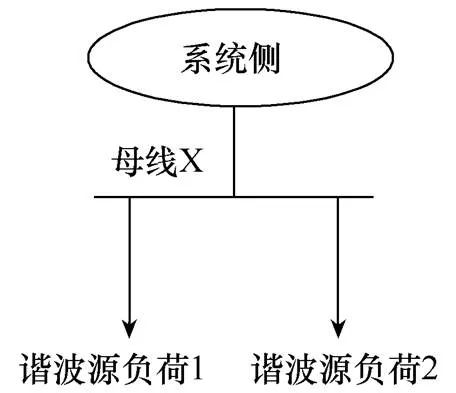
图1 单条母线X处接入谐波源负荷


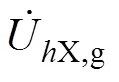
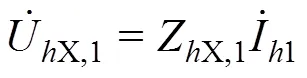
显然,根据式(1),、与3个相量可用如图2所示的向量关系表示。
关注谐波源负荷Load1在母线X处产生的次谐波电压责任为
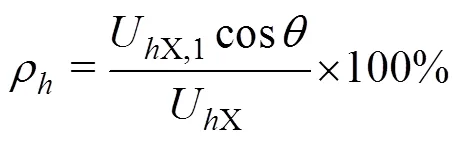
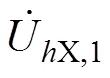
1.2 多点等值模型
图3所示为某配电网中含有多个谐波源负荷的示意图,用来分析第2类多点等值模型划分母线电压谐波责任问题。
进一步,乡愁的寄托需要载体:特色乡村建筑、传统节庆活动、乡村景观空间、居住空间、特色饮食等。纵观法国乡村旅游一个多世纪的发展,居住与饮食是让旅游者更能切身体验乡愁的物质载体,也是目的地经济的重要来源,因此,笔者认为“乡居”是发展的关键环节;在体验的同时,若能让旅游者引发思念与留恋,则会促进目的地的可持续发展,这有赖于更深层次的产品开发与整合,如参与制作、品鉴与销售等系列活动,产生“乡思”的情感依恋,从而形成促进乡村旅游发展的动力机制(如图4所示)。

图3 配电网中含有多个谐波源负荷的示意图

由于已经确定了系统中所有主要谐波源,所以此时系统背景谐波电压相对主要谐波源产生的谐波电压将是很小的量,可以忽略不计。
4个主要谐波源负荷在母线1处产生的谐波电压表达式:
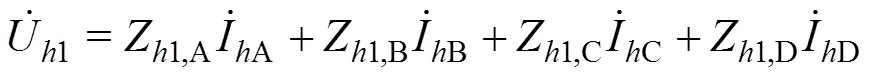
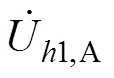
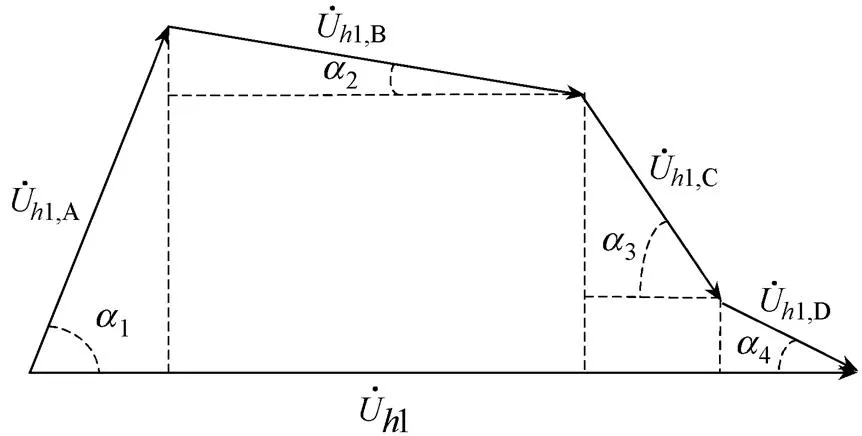
图4 5个相量的关系图
1、2、3和4分别表示各谐波源在母线1处产生的谐波电压分量与母线1处总谐波电压的相对相角。根据向量图,就可以计算出4个谐波源在关注母线1处产生的次谐波电压责任,其定义与单点等值模型中谐波责任定义相同。此外,多点等值模型划分谐波电压责任的关键,同样是准确估计各谐波源负荷与关注母线之间的次谐波阻抗。
2 算例比较验证
下面是对2类母线电压谐波责任划分模型的算例仿真,并进行比较分析。
本文以5次谐波为例进行分析,设置3个主要谐波源负荷,分别记作谐波源L1(11母线处)、谐波源L2(11母线处)与谐波源L3(9母线处)。关注母线为11母线,关注谐波源为L1。仿真时间为360min,1min 1个样本点,共采集360个样本点。
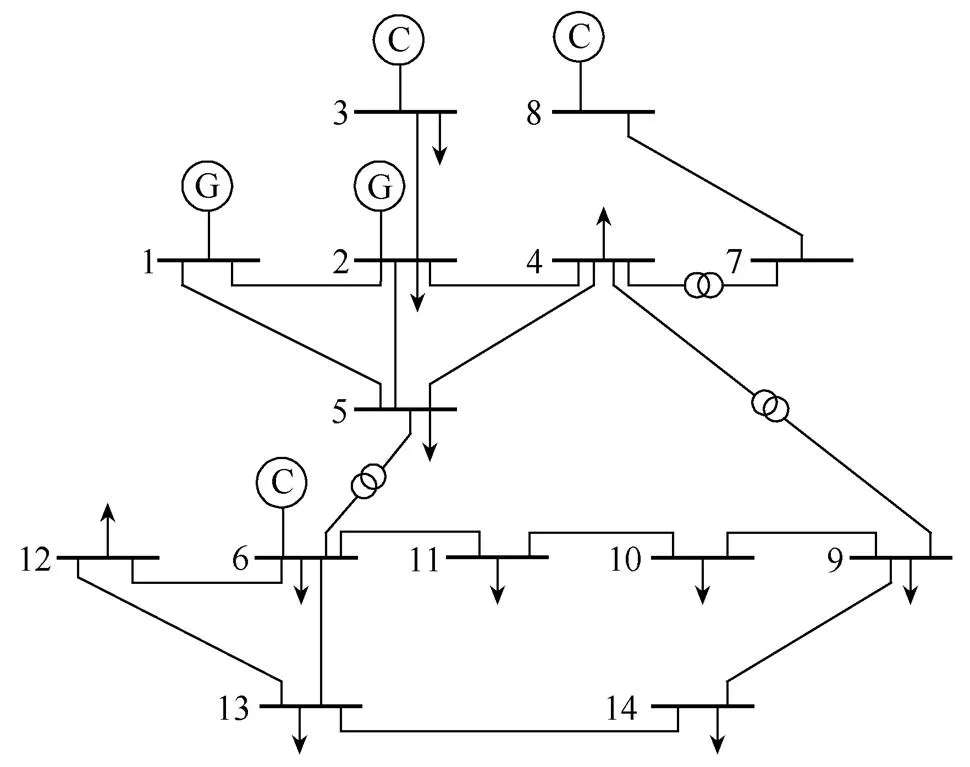
图5 IEEE 14节点测试系统
2.1 算例1
谐波源L1注入的5次谐波电流如图6所示,谐波源L2谐波电流幅值和相角分别为4.84A和66°,L3幅值和相角分别为9.84A和56°。谐波源L2和L3产生的谐波电压作为恒定的背景谐波电压。表1为多种单点等值模型计算的关注谐波源L1在关注母线11处的谐波电压责任计算值。
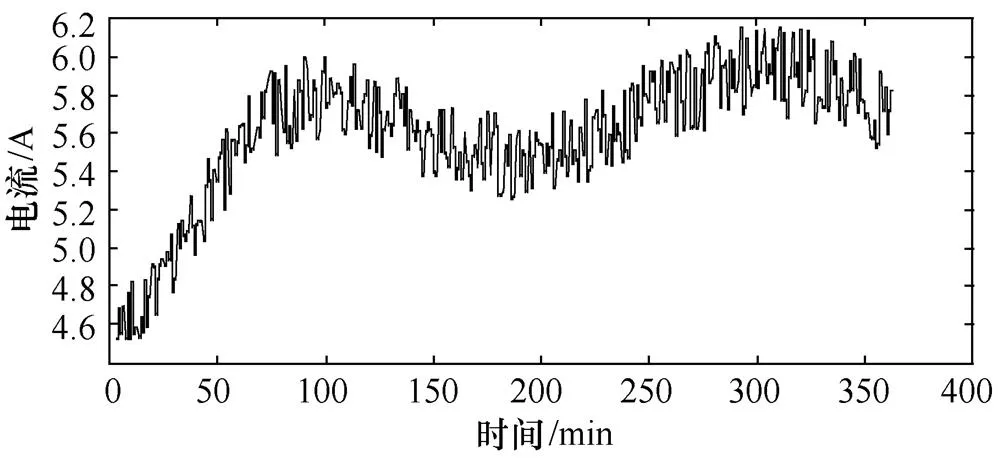
图6 谐波源L1注入的5次谐波电流
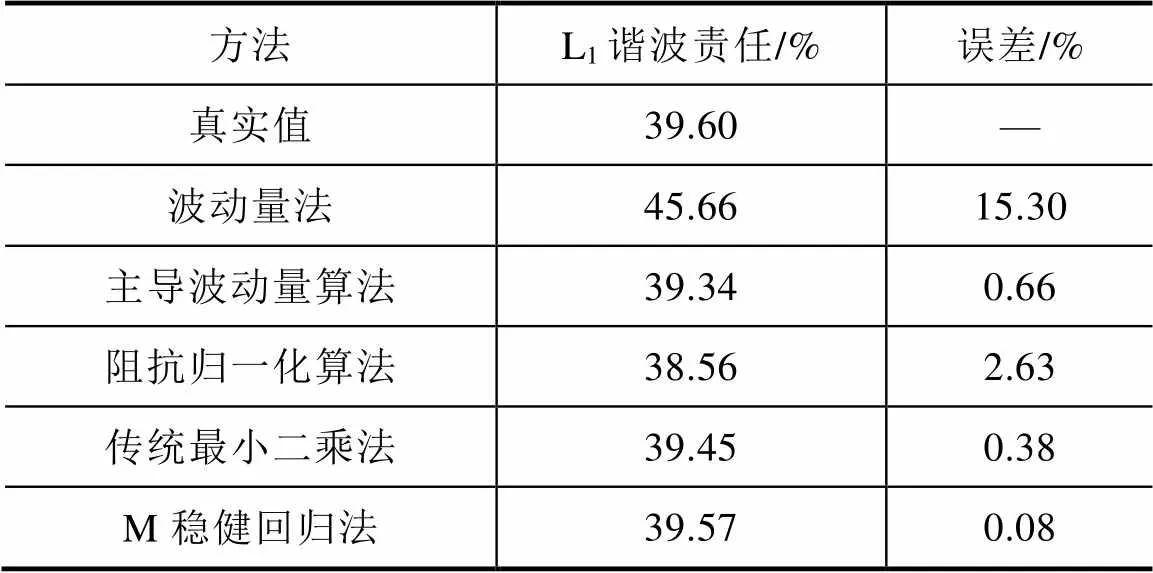
表1 谐波源L1的谐波责任计算值
由表1数据可知,当背景谐波恒定时,单点等值模型计算的L1谐波责任准确度都比较高,说明了单点等值模型比较适合计算系统主要谐波源情况未明,并且背景谐波电压波动不大情况下的单母线处谐波源产生的谐波责任,以此判断用户侧和系统侧哪一方对谐波污染起主导作用。
2.2 算例2
谐波源L1注入的5次谐波电流保持不变,谐波源L2和L3谐波电流分别如图7和图8所示。将L2和L3产生的谐波电压视为波动的背景谐波电压。表2为单点等值模型计算的谐波源L1在关注母线11处的谐波电压责任。表3为应用多点等值模型计算的3个谐波源各自的谐波责任。

图7 谐波源L2注入的5次谐波电流

图8 谐波源L3注入的5次谐波电流
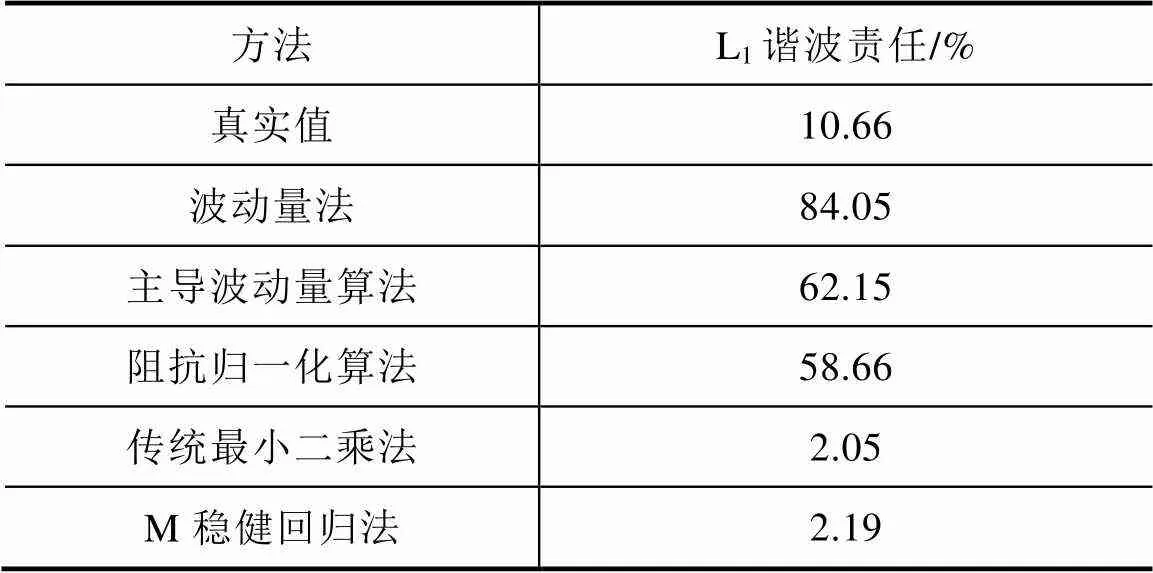
表2 谐波源L1的谐波责任计算值

表3 3个谐波源各自谐波责任计算值
观察表2和表3中数据可以发现,当背景谐波电压剧烈波动时,单点等值模型无法准确计算出谐波源L1的谐波责任,而此时多点等值模型不仅计算出L1的责任,其他两个谐波源在母线11处的谐波责任准确度也很高,这很好地弥补了单点等值模型在系统背景谐波波动较大时计算谐波责任出错的缺陷。因此,当准确知道系统中谐波源情况时,多点等值模型可以更好地划分母线电压谐波责任。
2.3 算例3
谐波源L1和L3注入的5次谐波电流保持不变,谐波源L2的谐波电流与L1注入的5次谐波电流相同如图6所示。当采集的谐波源负荷产生的谐波电流具有较强相关性时,利用多点等值模型计算各谐波源谐波电压责任。
此时,谐波源L1、L2和L3的真实责任分别为46.05%、46.05%和6.23%。利用传统最小二乘多元线性回归方法计算的3个谐波源谐波责任出错,而M稳健回归方法由于需要进行迭代计算,数据的严重相关性导致其迭代次数过多,也无法得出准确结果。由此可见,多点等值模型虽然在一定程度上弥补了单点等值模型的缺点,但是当谐波电流数据存在较强相关性时,同样无法得出准确的结果。这也是多点等值模型最大的不足。
3 结论
本文首先分析比较了两类母线电压谐波责任划分的模型。通过仿真算例的分析表明,单点等值模型适合划分系统背景谐波电压波动较小情况下的谐波污染责任。而当系统中所有主要谐波源情况已知时,多点等值模型可以避免单点等值模型因背景谐波电压波动剧烈带来的谐波阻抗估计误差偏大的缺点,从而更准确地划分每个谐波源在关注母线处产生的谐波电压责任。但是当谐波源电流数据之间存在较强相关性时,多点等值模型无法准确计算谐波责任。因此,在划分母线电压谐波责任时,要根据不同场合选择合适的模型,从而提高谐波责任划分的准确度。
[1] 李丽, 马宏忠, 姜宁, 等. 基于改进偏最小二乘法的系统谐波阻抗及谐波发射水平估算[J]. 电力系统保护与控制, 2011, 39(1): 92-95, 131.
[2] Xu W, Liu Y. A method for determining customer and utility harmonic contribution at the point of common coupling[J]. IEEE Transactions on Power Delivery, 2000, 15(2): 804-811.
[3] Pfajfar T, Blazic B, Papic I. Harmonic contributions evaluation with the harmonic current vector method[J]. IEEE Transactions on Power Delivery, 2008, 23(1): 425-433.
[4] 苗长新, 冯学俊, 马士亮, 等. 基于独立分量分析和互信息的多谐波源定位[J]. 电测与仪表, 2014, 51(11): 60-64.
[5] Chun L, Wilsun X. On defining harmonic contributions at the point of common coupling[J]. IEEE Transactions on Power Delivery, 2009, 24(1): 285-292.
[6] Mazin H E, Xu W, Huang Biao. Determining the harmonic impacts of multiple Harmonic-Producing loads[J]. IEEE Transactions on Power Delivery, 2011, 26(2): 1187-1195.
[7] 惠锦, 杨洪耕, 叶茂清. 多谐波源条件下的谐波污染责任划分研究[J]. 中国电机工程学报, 2011, 31(13): 48-54.
[8] 华回春, 贾秀芳, 张韶光. 谐波责任定量评估的邻域多点测量方法[J]. 电网技术, 2014, 38(2): 502-508.
[9] 贾秀芳, 张韶光, 华回春, 等. 部分线性核估计方法在谐波责任分摊问题中的应用[J]. 电力系统自动化, 2015, 39(3): 63-68.
[10] 孙媛媛, 尹志明. 基于M估计稳健回归的多谐波源责任区分[J]. 中国电机工程学报, 2012, 32(31): 166-173, 233.
[11] 张龙, 陈西平, 李洪杰, 等. 谐波阻抗和背景谐波电压估算方法的对比研究[J]. 电气技术, 2014(8): 1-6.
[12] 师洪涛, 卓放, 杨祯, 等. 基于改进正弦调制电流注入的三相交流电源系统谐波阻抗测量研究[J]. 电工技术学报, 2015, 30(8): 257-264.
[13] 邱思语, 杨洪耕. 改进的加权支持向量机回归的谐波发射水平估计方法[J]. 电工技术学报, 2016, 31(5): 85-90.
[14] Yang H, Pirotte P, Robert A. Harmonic emission levels of industrial loads statistical assessment[C]//CIGRE Proceedings. Paris: International Council on Large Electric Systems, 1996: 36-306.
[15] 华回春, 贾秀芳, 安海清. 背景谐波波动情况下的谐波责任定量计算[J]. 电测与仪表, 2014, 51(7): 1-8.
[16] 惠锦, 杨洪耕, 叶茂清. 基于阻抗归一化趋势判别的谐波发射水平估计[J]. 中国电机工程学报, 2011, 31(10): 73-80.
[17] 陆伟明, 聂一雄, 吕梦丽. 谐波阻抗测量及谐波源识别方法的探讨[J]. 电气技术, 2015, 16(5): 62-65, 69.
[18] 艾永乐, 郑建云. 基于谐波有功功率贡献量的主谐波源定位[J]. 电力系统保护与控制, 2015, 43(7): 16-22.
Simulation comparison between two models of the harmonic voltage contributions determination of the concerned bus
An Haiqing Yue Na Xing Yuxin
(State Grid Jibei Electric Power Company Limited Maintenance Branch Company, Beijing 102488)
The models of harmonic voltage contributions determination are divided into two categories. The first model is called a single-point equivalent model, which is to allocate the harmonic voltage contributions between the concerned harmonic sources at the single point of common connection and the grid side. The second model is called a multi-point equivalent model, which is to determine the harmonic contributions of the multiple harmonic sources at the distal end of a particular bus. The characteristics and their application of occasions of the two models are theoretically analyzed and compared in detail in this paper. Several case studies based on the IEEE 14-bus standard test system are conducted. The simulation results show that the single-point equivalent model is suitable for the harmonic voltage contributions determination when the background harmonic voltage fluctuation is constant or small. However, when all the main harmonic sources in the system are known, the multi-point equivalent model can avoid the shortcomings of the single-point equivalent model, i.e. the error of the harmonic impedance estimation is too large which is caused by the background harmonic voltage fluctuation, so that the harmonic voltage contributions of each harmonic source at concerned bus can be determined more accurately.
power quality; harmonic voltage contributions; harmonic impedance; background harmonic voltage; equivalent model
2018-04-25
安海清(1990-),男,江苏省无锡市人,硕士研究生,工程师,主要研究方向为电能质量分析与控制。

