基于MRAS与逆系统解耦的永磁同步电动机复合控制

张军兆 王新庆 李晓亮



基于MRAS与逆系统解耦的永磁同步电动机复合控制

张军兆 王新庆 李晓亮

（北京星航机电装备有限公司智能电气事业部，北京 100074）

本文通过对MRAS模型分析，提出了一种基于逆系统的MRAS模型。通过反馈构建出可调模型的逆系统，实现可调模型的线性化和解耦，可以单独控制和调节可调模型中旋转坐标d、q轴上的估计电流。本文还详细介绍了基于逆系统的MRAS永磁同步电动机控制系统的建立并进行了仿真。仿真结果表明，该控制系统能有效的抑制扰动具有良好的动态性能和鲁棒性，在转速估计方面也有良好的精度。

永磁同步电动机；逆系统；模型参考自适应系统；解耦

永磁同步电动机具有高转矩惯性比、功耗小和重量轻等优点，是现代工业中应用比较广泛的电气传动系统。其中，转子转速和位置一直控制系统中重要的参数。一般通过安装位置传感器来检测电动机的速度和位置，但位置传感器存在成本高、安装困难、易受环境影响等缺点。国内外学者提出了转子转速和位置检测的算法[1]。MRAS是其中比较成熟的转子转速和位置估计的算法之一，但MRAS模型中的参考模型和可调模型是建立在电动机的精确模型之上的，存在参数依赖性强、低速状态效果差、计算复杂、实现困难等问题。因此，要实现高性能的永磁同步电动机无速度传感器控制系统，先进的速度辨识方法是重要前提。

如果通过逆系统原理实现MRAS结构中可调模型的解耦，实现可调模型两个输出物理量单独调节，并可根据参考模型中相应的输出物理量调节，可调模型逼近参考模型的能力就会得到提高。

因此本文提出了将MRAS中的可调模型通过逆系统解耦，构成伪线性系统，可以单独的控制和调节可调模型中旋转坐标d、q轴的电流估计值，抑制可调模型中由于耦合带来的扰动和MRAS对参数变化的敏感的缺点，可以增强系统的动态性能、稳定性和抗扰动的性能。

1 PMSM数学模型分析

MRAS算法是建立在永磁同步电动机的数学模型之上的，通过坐标变换可以建立旋转坐标轴上的永磁同步电动机的数学模型，这样易实现MRAS模型的建立和控制。

1.1 PMSM在旋转坐标系下的模型[3]

在面装式永磁同步电动机中，定子有A、B、C三相对称且互差120°的绕组，取和电动机转子同步旋转的坐标系，其中以磁场基波励磁轴线（磁极轴线）为d轴，顺着转子旋转方向超前d轴90°为q轴，dq轴坐标系的空间坐标以d轴与A轴间的角度g来确定。忽略涡流和磁滞损耗，则永磁同步电动机在dq坐标系下的数学模型[4]如下。

电压方程为

磁链方程为

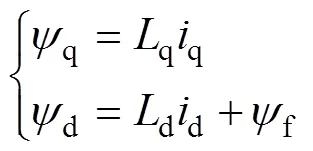
式中，为微分因子；d、q为d、q轴定子电压；d、q为d、q轴定子电流；d=q=为定子绕组自感；s为定子绕组电阻；d、q为d、q轴磁链；r为转子机械角速度；f为永磁体常数。

2 MRAS算法和逆系统分析

MRAS是20世纪50年代后期发展起来的，其是基于参考模型和可调模型来实现速度辨识，对电动机参数有很强的依赖性。

2.1 MRAS算法分析

MRAS的基本思想是构建一个含有待估计参数的可调模型和一个不含未知参数的参考模型[5]，然后通过调节可调模型逼近参考模型，两个模型具有相同物理意义的输出量。选取电动机模型为参考模型，输出量为旋转坐标系上的电流，通过变形式（1）可得参考模型：

令

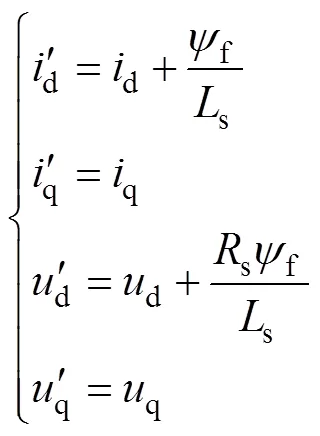
由式（3）、式（4）可得MRAS模型中的可调模型，即

将式（5）以估计值表示，可得

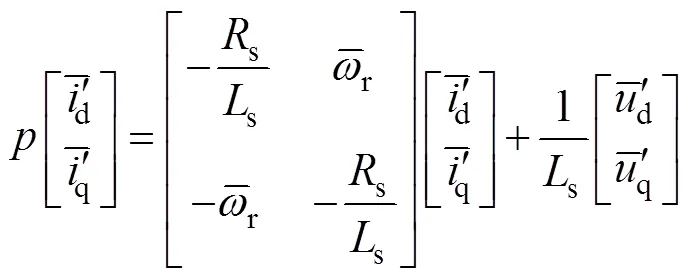
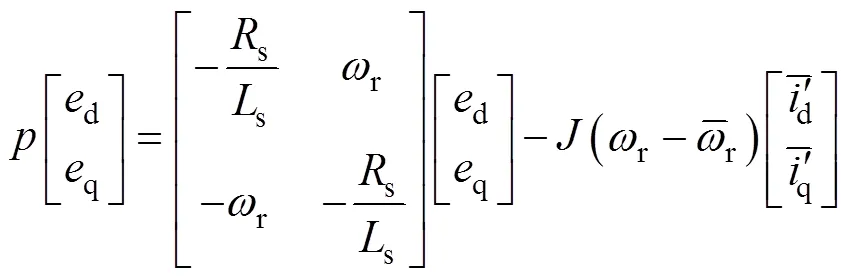
为使得系统稳定，根据波波夫超稳定理论[6]可得

式中，p、i为PI调节系数。

由式（5）至式（8）可以建立MRAS的自适应规律模型，如图1所示。

2.2 可调模型逆系统分析

一种基于反馈线性化和多变量解耦的方法——逆系统，可用于强耦合和非线性的系统中。一般对于一个系统，通常用原系统输入到输出函数的映射关系来描述，若采用从输出到输入的映射关系来表达，则构成原系统的逆系统。

图1 自适应律模型图

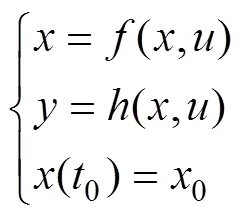
由上式及式（6）可知，MRAS的可调模型是一个三输入双输出的数学模型，输入为1、2、3，输出为1、2，可以确定可调模型的输入、输出量和状态量。

输入量为

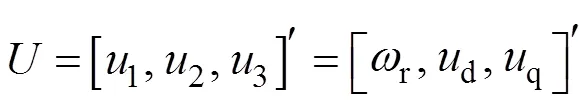
输出量为

状态量为

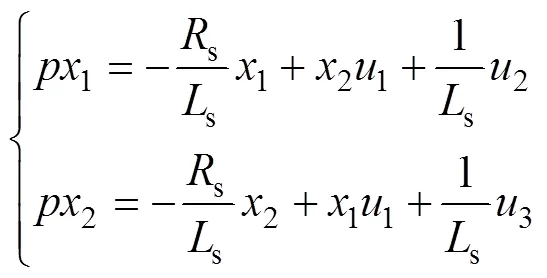
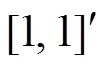
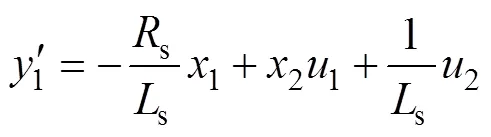
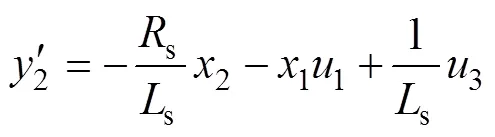
由式（14）、式（15）可得可调模型的逆系统：

将式（16）展开：

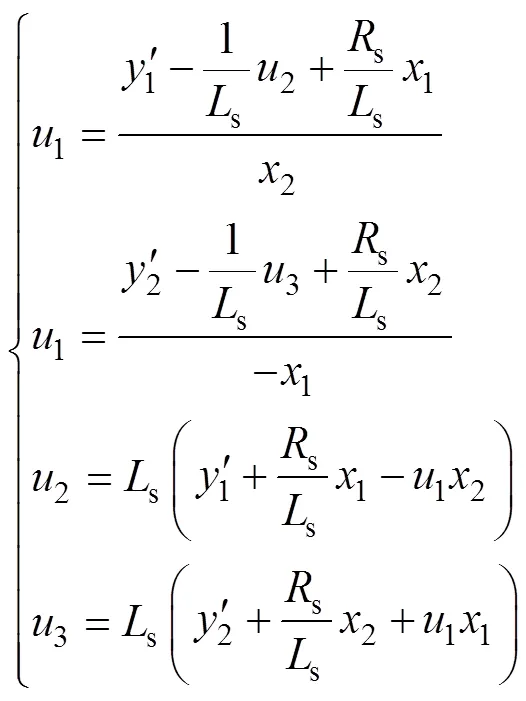
由式（16）可以看出，d、q逆系统中含有输入量，但是2、3可以通过采样定子电流的坐标变换可得，即相对于可调模型的逆系统而言是一个已知量，这样式（16）的输入量只有一个即1，式（17）含有两个关于输入量1的等式，其中式（17）中的第一个等式是通过式（14）求得，第二个等式是通过式（15）求得的，虽然两个等式中的1是同一个输入量，这里先看做成两个独立的量，且定义式（17）中第一个等式中的1为11，第二个等式中的1为12，这样相对于式（16），可调模型的逆系统是一个不含输入参数的双输入双输出的系统[8]，实现了系统的线性化和解耦，可以单独控制和调节。

3 PMSM矢量控制系统的构建

构建MRAS可调模型的逆系统，实现了可调模型的线性化和解耦[9]，可以提高系统抑制扰动的能力，更好地对速度进行跟踪，增强系统的动态性能和鲁棒性。

3.1 基于逆系统的MRAS模型的构建

根据可调模型的分析，结合MRAS的模型可以构建出基于逆系统的MRAS模型，如图2所示。

图2中的11和12经过PI后分别控制可调模型中相应等式中的r，这样就实现了可调模型的线性化和解耦。

3.2 永磁同步电动机矢量控制系统的构建

该模型中永磁同步电动机的矢量控制系统[10]包括了Clark模块、Park模块、MRAS模块、AD模块等功能模块，如图3所示。

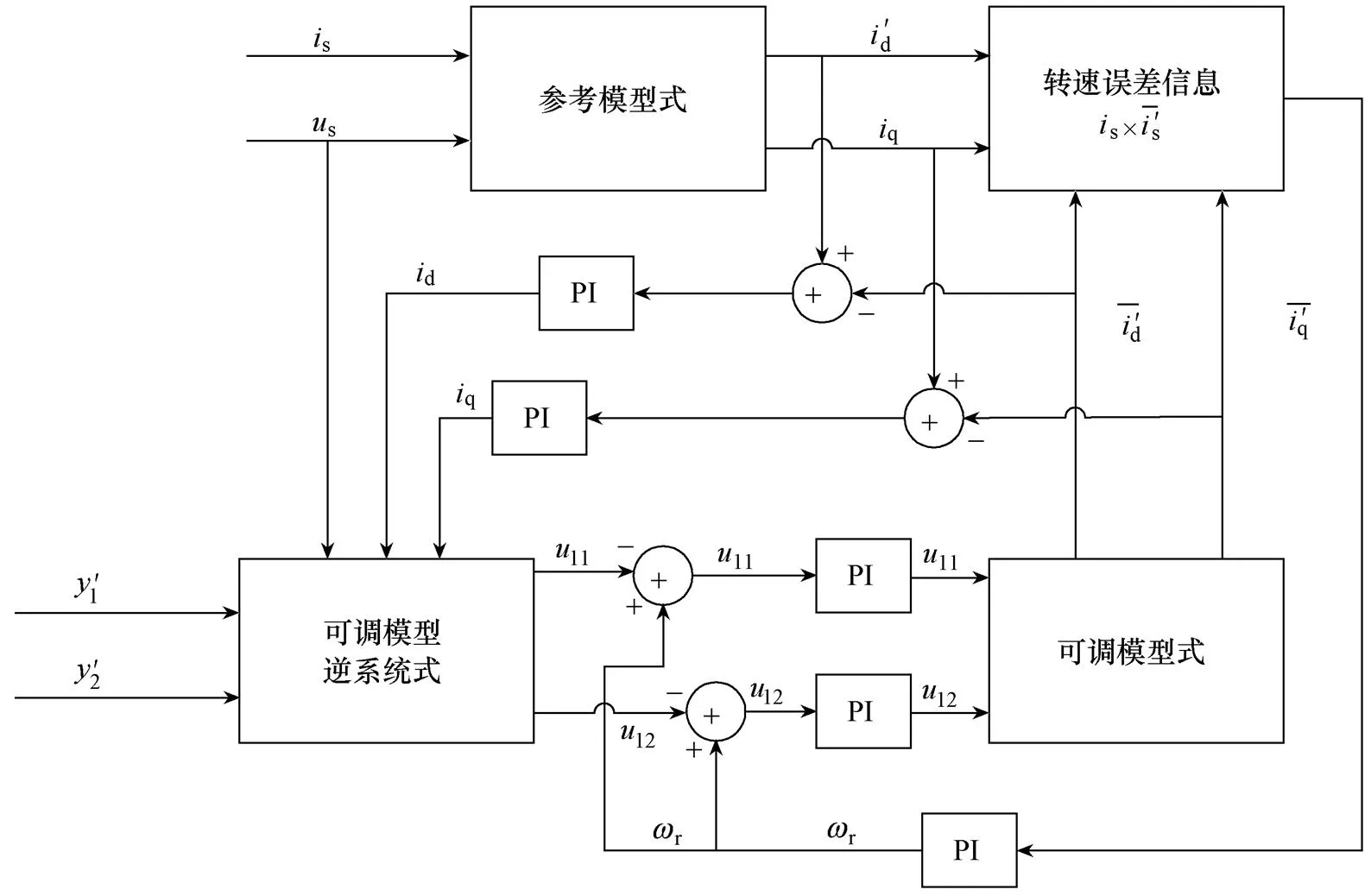
图2 基于逆系统的MRAS模型

图3 永磁同步电动机矢量控制系统

4 仿真结果分析

为了验证上述控制方案的可行性，按照图3所示的仿真模型进行了仿真实验[11]，仿真结果如图4所示。

仿真时电动机参数设置如下：=4W；d=q= 16×10-3H；=5；f=0.175Wb；=0.8×10-3kg·m2。

图4为加入逆系统的参考模块和可调模型的电流。在参考模型中没有加入逆系统解耦，可由图4得出参考模型电流d和q在加入扰动后，电流在很强的耦合下波动，波动范围和波形相似度较大，相比于参考模型，可调模型引入了逆系统解耦，虽然在可调模型电流d加入扰动后，可调模型电流q波动范围较小，且q电流的波形受d波形变化的影响较小。

图5和图6分别为基于逆系统解耦MRAS模型和MRAS模型的仿真转速曲线图。相比较两组图可得，没有加入逆系统解耦的MRAS模型系统的估计转速超调量很大，转速估计的跟随性差，在加入干扰后波动大且稳定时间较长。

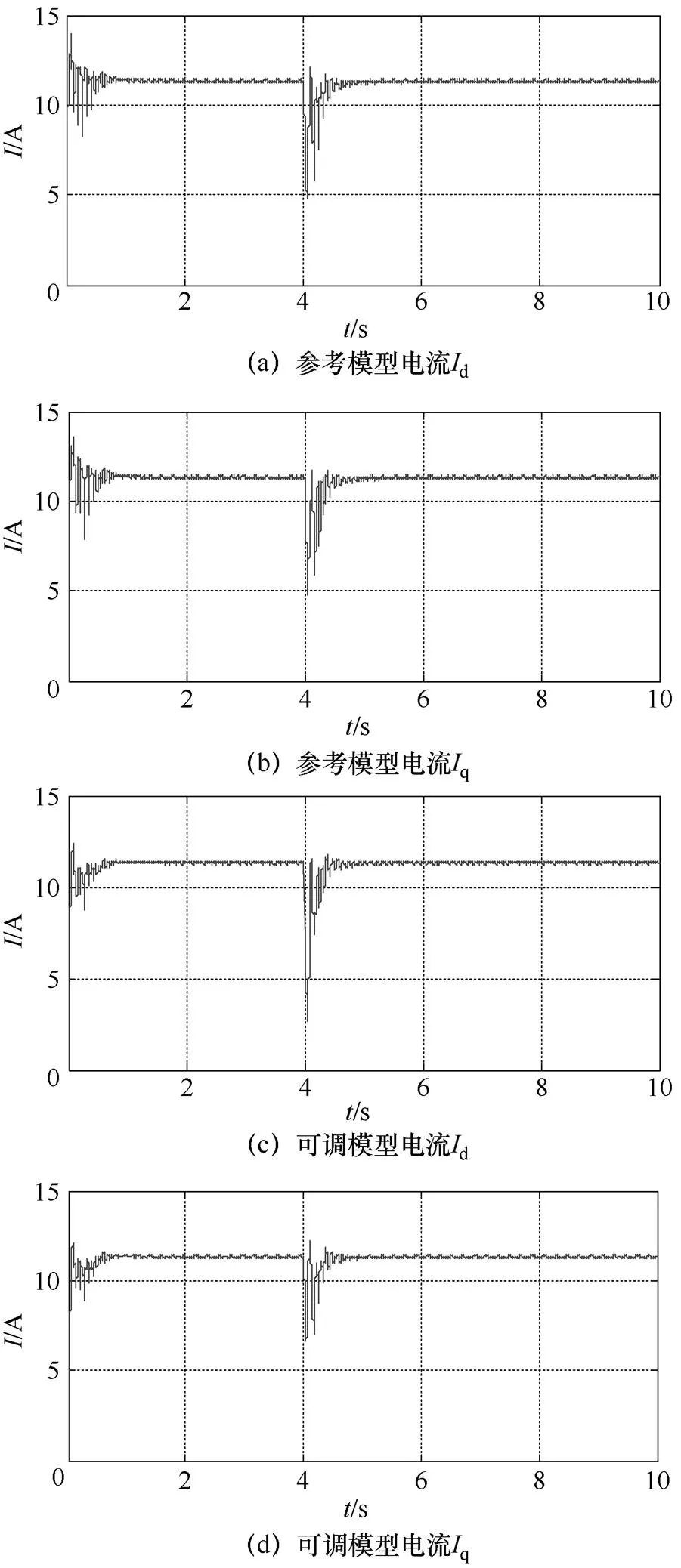
图4 加入逆系统的参考模型和可调模型电流

两种模型系统对比，响应时间大致相同，但加入逆系统模型响应更稳定。

在第4s至第4.3s期间，图5比图6中的曲线波动更小（注意两图纵轴量程差别），实际转速曲线跟随性好，估计精度也更高。从而保证了整个系统的鲁棒性优越于基于MRAS的永磁同步电动机矢量控制系统，也体现出基于逆系统的MRAS系统自我调剂能力和跟随能力以及估计精度优越于MRAS系统。

通过以上仿真分析比较可知，系统被引入逆系统解耦后，在一定程度上实现了解耦，抑制了扰动的干扰，有效地提高了系统的动态性能、鲁棒性和转速估计能力。

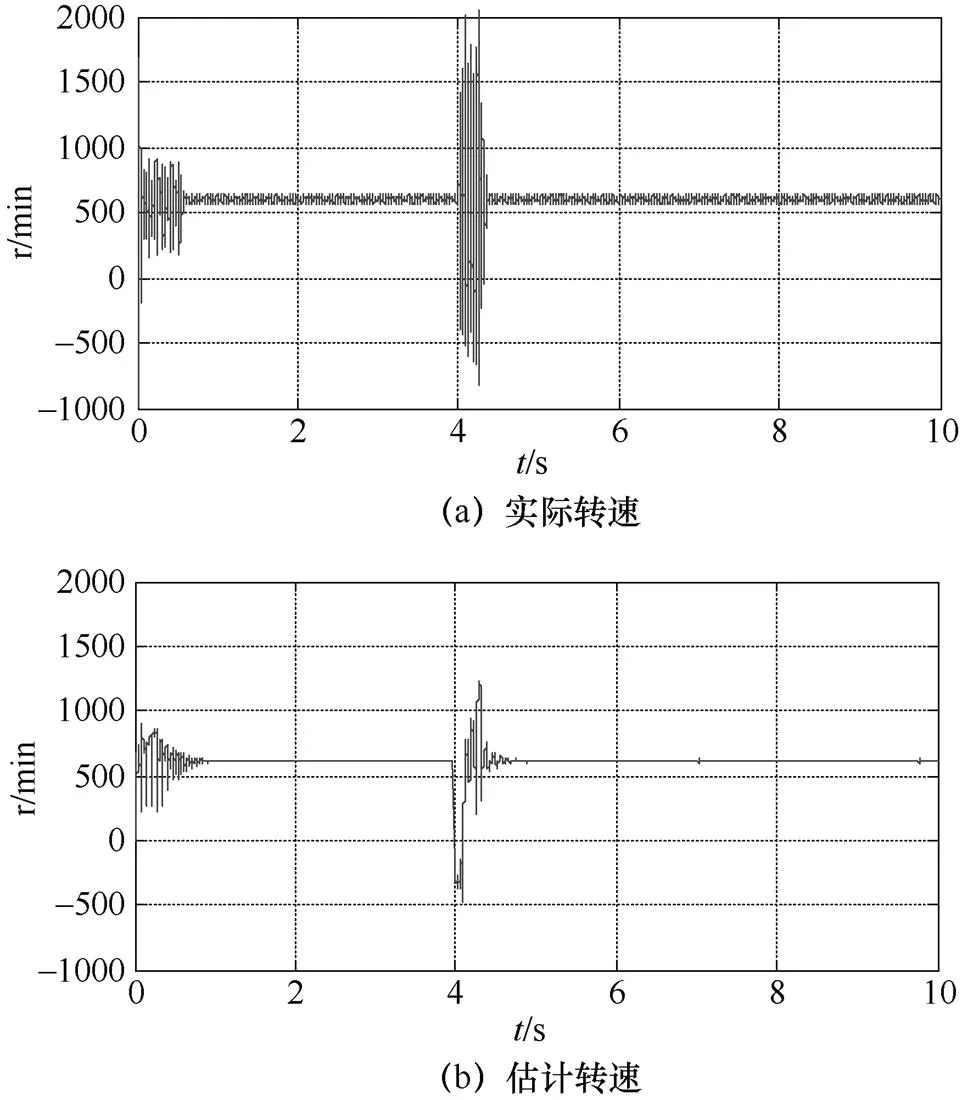
图5 加入逆系统的实际转速与估计转速

图6 MRAS模型的实际转速与估计转速

5 结论

基于逆系统MRAS的永磁同步电动机的矢量控制，本文详细介绍了基于逆系统MRAS模型的推导过程并进行了仿真，从仿真结果来看，本文介绍的基于逆系统MRAS模型的控制系统具有良好的转速估计性能和抑制扰动的能力，提高了整个系统的动态性能和鲁棒性。

[1] 王成元, 夏加宽. 电机现代控制技术[M]. 北京: 机械工业出版社, 2006.

[2] 刘毅, 谭国俊, 何凤有, 等. 基于NNs-MRAS无速度传感器双馈电机LQR控制[J]. 电工技术学报, 2014, 29(7): 140-146.

[3] 戴先中, 刘国海, 张兴华. 交流传动神经网络逆控制[M]. 北京: 机械工业出版社, 2007.

[4] 张润波, 林荣文, 高靖凯. 基于改进滑模观测器的PMSM无位置传感器的研究[J]. 电气技术, 2016, 17(1): 51-54, 61.

[5] 张兴华, 张翼. 永磁同步电机逆系统解耦控制[J]. 微电机期刊, 2007, 40(8): 9-12.

[6] 王君艳. 交流调速[M]. 北京: 高等教育出版社, 2006.

[7] 王正齐, 黄学良. 基于支持向量机逆系统轴承异步电动机非线性解耦控制[J]. 电工技术学报, 2015, 30(10): 164-170.

[8] 尹忠刚, 张迪, 蔡剑, 等. 基于三自由度内模控制的永磁同步电机矢量控制方法[J]. 电工技术学报, 2017, 32(21): 55-64.

[9] 邱佰平, 凌云. 基于MRAS的新型永磁同步电机的速度辨识方案[J]. 机电工程技术, 2009, 38(10): 32-35, 99.

[10] 王德贵. 永磁同步电机调速系统的模糊趋近律滑模控制[J]. 电气技术, 2015, 16(3): 10-14.

[11] 洪乃刚. 电力电子和电力拖动控制系统的MATLAB仿真[M]. 北京: 机械工业出版社, 2006.

Combined decoupling control of permanent magnet synchronous motor based on MRAS and inverse system

Zhang Junzhao Wang Xinqing Li Xiaoliang

(Beijing Xinghang Mechanical & Electrical Equipment Co., Ltd, Beijing 100074)

From the analysis of MRAS, it has presented a control method based on which is a combination of inverse system and MRAS. The variable model based on inverse system is realized by feedback which is making variable model linearization and decoupling as well as adjusting and controlling the variable model's current which was estimated by d-axis and q-axis. It also illustrated how to build a vector control system of PMSM based on the combination of inverse system and variable model. The emulation turned out that this vector control system could inhibit the disturbance effectively and have a good dynamic performance and robustness as well as the estimation of speed.

permanent magnet synchronous motor; inverse system; model reference adaptive system; decoupling

2018-05-11

张军兆（1985-），男，工学硕士，研发工程师，主要研究方向电力电子与电气传动以及电能质量治理。