基于非支配排序的改进粒子群算法的含分布式电源的配电网规划

何 頔 罗 进 唐世虎 程 实 李彩云



基于非支配排序的改进粒子群算法的含分布式电源的配电网规划

何 頔 罗 进 唐世虎 程 实 李彩云

（国网南充供电公司，四川 南充 637000）

随着分布式电源（DG）渗透率的不断提高,在进行配电网规划时不得不将DG考虑进配电网一起规划。本文在对比了基本粒子群算法（PSO）易陷入局部最优的缺陷之后，利用小生境技术寻找全局最优，再采用基于非支配排序的改进粒子群算法（NSPSO）对含DG的配电网进行了规划。本文建立以分布式电源投资和运行成本最少、有功网损最小、电压稳定裕度最大的目标规划模型，并且结合对IEEE 69节点配电网的仿真分析，对比算法结果，从经济性和稳定性两方面都证明了基于非支配排序的改进粒子群优化算法在含DG的配电网规划方面有一定的优势。

配电网规划；分布式电源；小生境技术；非支配排序；改进粒子群算法

“十二五”期间，国家电网的发展有很多的机遇，但同时也存在很多挑战。在节能减排、节约利用资源的潮流中，可再生能源分布式电源（DG）的发展成了不可阻挡的趋势。大体上来说，分布式电源（DG）是集成或单独使用的、靠近用户的小型模块化发电设备，多为容量在50MW以下的小型发电机组。其中分布式电源（DG）包括太阳能、风能、水能、小型燃汽轮机、燃料电池等。受地理和经济条件的限制，除风电以外，其他各种可再生能源还不容易做到集中的大规模利用。即便是对于技术最为成熟的风力发电，也只有少数风资源极为丰富的地区才能达到和常规发电相比的规模。由此可见，大量利用可再生能源发电的重要手段是采用分布式发电，不仅能实现能源利用的可持续发展，还能解决温室气体排放和环境污染的问题。因此，如何合理可靠的利用分布式电源成为众多学者研究的 对象。

由于DG的接入，传统的配电网规划方法不能满足需要。故国内外学者提出了许多优化方法。文献[1]采用矩阵编码、修复不可行解的改进遗传算法研究了分布式电源的安装位置和容量，使得经济效益和环境效益最优。文献[2-3]应用改进粒子群优化算法进行配电网分布式电源（DG）规划，并结合罚函数法将DG规划问题转化成无约束求极值问题，从而有效地提高了改进粒子群优化算法的全局收敛能力和计算精度。与传统相比，遗传算法具有收敛性好、鲁棒性高等优点，但容易陷入“早熟”；粒子群算法收敛速度快、算法简单，但易陷入局部最 优[4-6]。

针对以上的种种不足，本文提出了一种基于非支配排序[7]的改进粒子群算法（NSPSO），利用小生境技术寻找全局最优，并对IEEE 69节点配电系统进行了验证，其分布式电源的运行与投资成本和电压稳定裕度都比基本粒子群算法（PSO）有一定的提高。

1 分布式电源对配电网的影响

将分布式电源接入配电网后，在一定程度上改善了能源的紧张，因为它具有多样性和可再生性，更由于它是清洁能源，也提高了环境效益[8-10]。接入DG后，在稳态情况下（视负荷恒定不变），馈线上的传输功率减少以及DG输出的无功的支持，使得沿馈线的各负荷节点处的电压有所提高。电压的稳定性与接入的DG的位置及总容量的大小有关。如果DG仅作为备用电源，就可以提高系统供电的可靠性，但如果DG与电网并联运行，就有可能降低系统的可靠性。DG的出现会提高配电网的故障电流水平。综上所述，分布式电源接入配电网以后有利有弊，只有合理的确定分布式电源的位置与容量，才能充分发挥分布式电源的优势。

2 含分布式电源的配电网规划模型

2.1 总投资与运行成本目标函数

由于分布式电源的接入，增加了设备和投资运行成本，本文建立了以分布式电源总投资与运行成本最小的目标函数。数学模型可由下式表示：

式中，为分布式电源设备使用年限；为贴现率；1为单位分布式电源的投资成本；2为单位分布式电源的运行成本；g为分布式电源的总容量。

2.2 有功网损

分布式电源（DG）接入后，一般靠近用户侧，网损可能会降低。本文建立了有功网损最小的目标函数，其数学模型如下式：

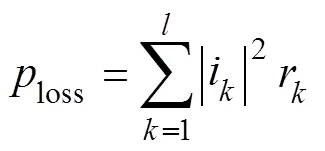
式中，loss系统有功网损；为支路数；i为支路电流；r为支路电阻。

2.3 电压稳定裕度目标函数

将分布式电源接入配电网以后，可能引起某些负荷节点电压不稳定，因此本文建立了电压稳定裕度函数来衡量电压的稳定性，也可以约束分布式电源接入电网的容量和位置，从而提高电网的可靠 性[11]。其数学模型公式如下：

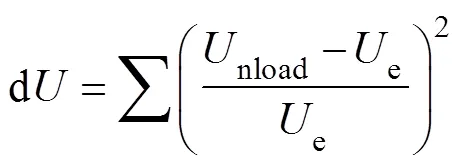
式中，nload为负荷不为零的节点的电压值；e为节点负荷期望电压值。

2.4 约束条件

1）容量约束

2）电压约束

3）电流约束

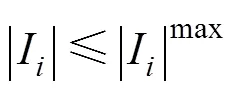
3 基于非支配排序的改进粒子群算法

粒子群优化算法（particle swarm optimization, PSO）是通过模拟鸟群觅食行为而发展起来的一种基于群体协作的随机搜索算法[12-14]。本文采用非支配排序选择适应度值高的进入下一代种群，提高收敛速度。小生境技术就是将每一代个体划分为若干类，每个类中选出若干适应度较大的个体作为一个类的优秀代表组成一个群，再在种群中以及不同的种群之间杂交、变异产生新一代个体群，提高全局寻优能力。粒子群算法中粒子的位置和速度更新公式如下：

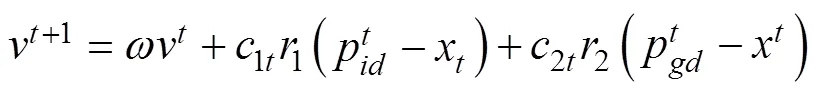
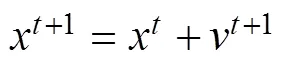
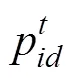
惯性权重的更新公式为

式中，为第代时的惯性权重；min=0.4为起始惯性权重；max=0.9为终止惯性权重；为迭代次数；为当前迭代次数。

本文算法流程如下：

1）输入配电网网络结构参数，确定电压、电流、功率等约束条件；初始化粒子群，设置种群数量、最大迭代次数、目标函数个数，粒子速度和位置的上下限；设置=0，随机生成初始解。

2）对第代种群使用前推回代法[16]进行潮流计算，求出各目标函数、d、loss的值。

3）对目标函数值进行排序，根据排序计算个体适应度的值，再用小生境技术寻找最好的全局最优解。

4）粒子速度和位置的更新，本文采用动态惯性权重更新公式。

5）对更新后的种群进行潮流计算，计算目标函数值。

6）让父代和子代种群混合。

7）采用非支配排序法对各目标函数进行排序，根据排序结果选择下一代种群。

9）输出最优解。

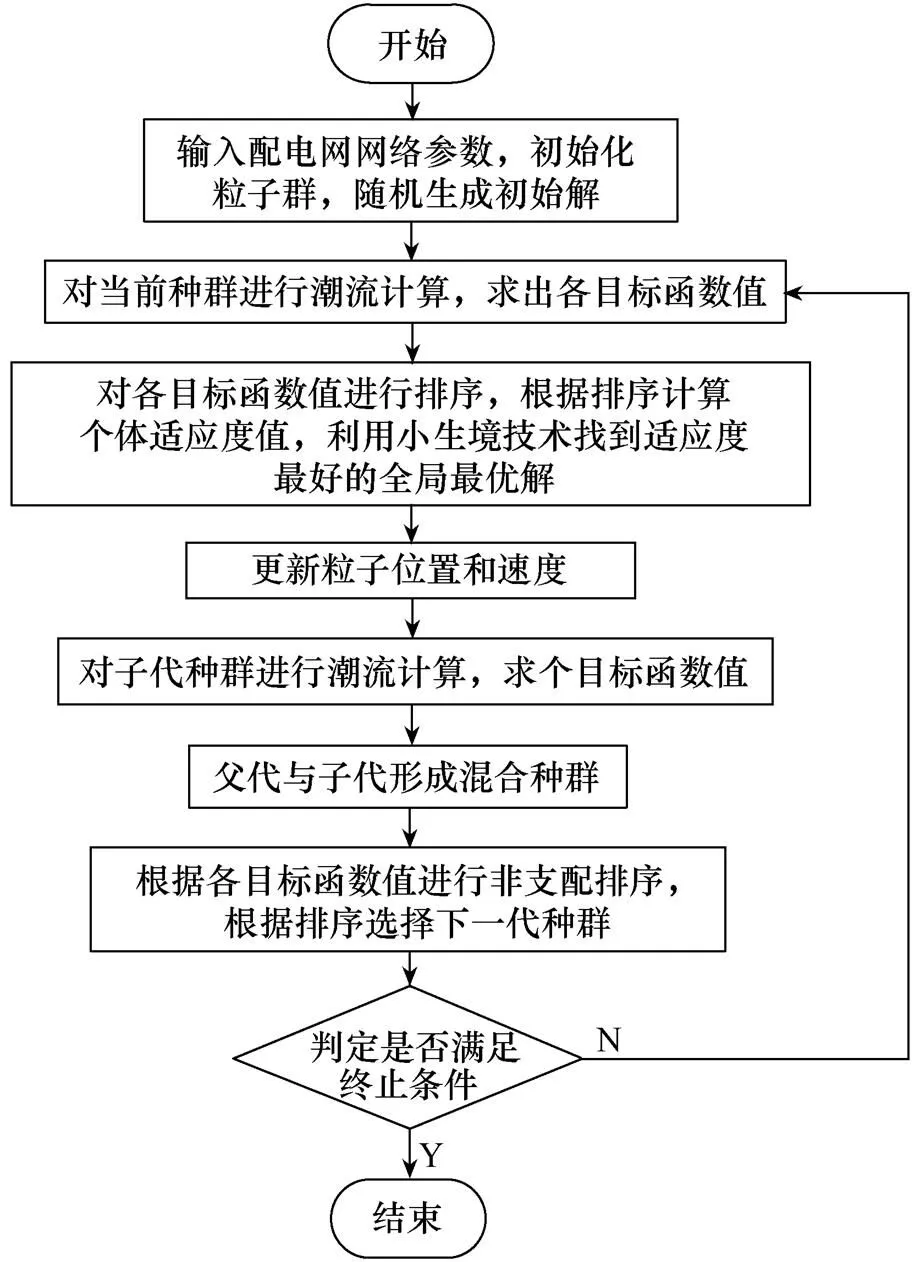
图1 迭代流程图

4 算例仿真及结果分析

本文采用IEEE 69节点配电网系统进行仿真测试。69节点配电系统结构如图2所示。该系统负荷总的有功功率和无功功率分别为3802.19kW和2694.60kvar。粒子群优化算法的参数设置：种群粒子数目=90，惯性系数min=0.4和max=0.9，1t= 2.5+(0.5-2.5)/和2t=0.5+(2.5-0.5)/为动态学习因子，最大迭代次数=200。

图2 69节点配电网测试系统接线图

为了验证非支配改进粒子群算法的可行性，本文与基本粒子群算法作了对比，结果证明改进的NSPSO在配电网规划中有一定的优势，对比结果见表1。两种算法的仿真的粒子最优图形分别如图3、图4所示。

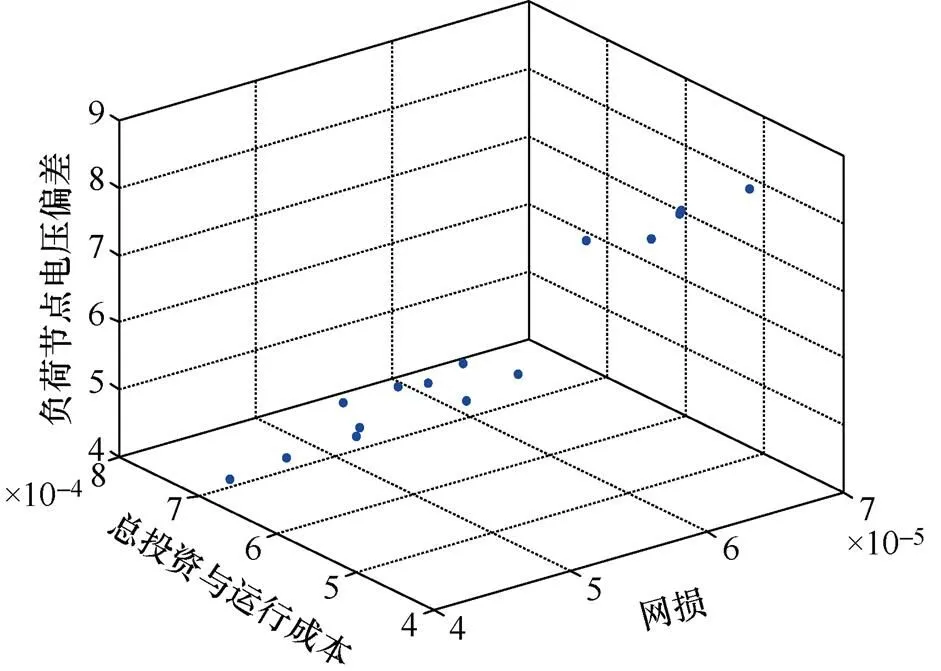
图3 基本PSO算法仿真图

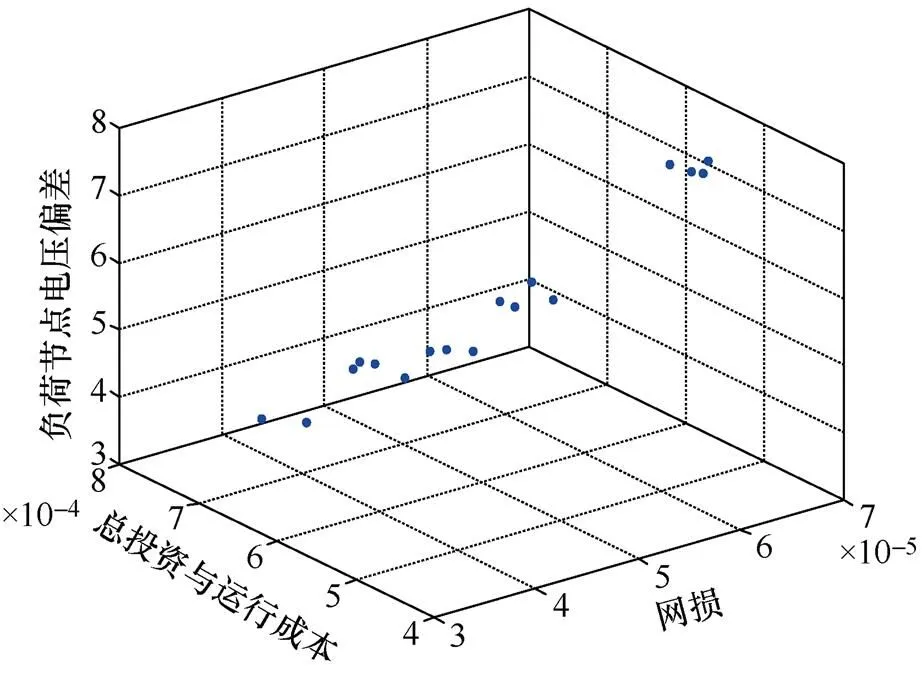
图4 改进的NSPSO算法仿真图

表1 69节点配电测试系统计算结果对比

从表1中可以看出改进的非支配粒子群算法，无论从DG的投资运行成本、网络的有功损耗还是电压稳定裕度诸方面，都在基本粒子群算法的基础上有一定的改善。这证明，改进的非支配粒子群算法在含DG的配电网规划中国是可行的。

5 结论

本文将改进的非支配粒子群算法用于IEEE 69节点配电系统，体现出该算法寻优能力。本文只考虑了DG投资成本、有功网损、电压稳定裕度，而没有考虑环境成本和购电成本等许多方面。因此，含分布式电源（DG）的配电网规划还有待进一步的研究。

[1] 麻秀范, 崔换君. 改进遗传算法在含分布式电源的配电网规划中的应用[J]. 电工技术学报, 2011, 26(3): 175-181.

[2] 徐卫星. 基于改进粒子群算法的分布式电源优化配置[J]. 电气技术, 2015, 16(12): 71-75.

[3] 汪兴旺, 邱晓燕. 基于改进粒子群算法的配电网分布式电源规划[J]. 电力系统保护与控制, 2009, 37(14): 16-20, 40.

[4] 张节潭, 程浩忠, 姚良忠, 等. 分布式风电源选址定容规划研究[J]. 中国电机工程学报, 2009, 29(16): 1-7.

[5] 叶在福, 单渊达. 多种群遗传算法在电网扩展规划中应用的改进[J]. 电力系统及其自动化学报, 1999, 11(S1): 55-61.

[6] 周巧俏, 汤云岩, 海晓涛. 基于改进自适应遗传算法的分布式电源的选址和定容[J]. 陕西电力, 2010, 38(6): 40-44.

[7] 冯士刚, 艾芊. 带精英策略的快速非支配排序遗传算法在多目标无功优化中的应用[J]. 电工技术学报, 2007, 22(12): 146-151.

[8] 王敏, 丁明. 含分布式电源的配电系统规划[J]. 电力系统及其自动化学报, 2004, 16(6): 5-8, 23.

[9] Wang C S, Nehrir M H. Analytical approaches for optimal placement of distributed Generation sources in power systems[J]. IEEE Transactions on Power Systems, 2004, 19(4): 2068-2076.

[10] 陈国恩, 张磊, 王跃强. 分布式电源智能调控系统研究与实践[J]. 电气技术, 2016, 17(3): 90-93.

[11] 康鲁豫, 朱顺, 刘刚. 考虑电压稳定和网损的分布式电源最优选址和定容[J]. 电气技术, 2015(2): 1-5, 22.

[12] 耿彦波. 基于粒子群算法的电力系统无功优化[D]. 北京: 华北电力大学, 2009.

[13] 徐玉琴, 李雪冬. 基于改进免疫克隆选择算法的含分布式电源配电网规划方法[J]. 电网技术, 2010, 34(8): 97-101.

[14] 王成山, 陈恺, 谢莹华, 等. 配电网扩展规划中分布式电源的选址和定容[J]. 电力系统自动化, 2006, 30(3): 38-43.

[15] 王照生. 基于惯性因子动态化的一种改进型粒子群算法[J]. 学园, 2013(15): 54-55.

[16] 张立梅, 唐巍. 计及分布式电源的配电网前推回代潮流计算[J]. 电工技术学报, 2010, 25(8): 123-130.

Distribution network planning with distributed power supply based on non dominated sorting of improved particle swarm algorithm

He Di Luo Jin Tang Shihu Cheng Shi Li Caiyun

(Nanchong Power Supply Company of SGCC, Nanchong, Sichuan 637000)

With the continuous improvement of distributed power supply (DG) permeability, in the distribution network planning are having to DG considered in distribution network planning together. In contrast the basic particle swarm optimization (PSO) after the defect of easily plunged into local optimum, by using niche technology to find the global optimal, and the improved particle swarm algorithm based on non dominated sorting (NSPSO) to contain the DG distribution network planning. This paper establish a distributed power investment and operation cost minimum, active minimum network loss and voltage stability margin the biggest goal programming model, and combined with the simulation analysis of the IEEE 69 node distribution network, contrast algorithm as a result, from two aspects of economy and the stability is proved that the improved particle swarm optimization algorithm based on non dominated sorting in the planning of the distribution network with DG has a certain advantage.

distribution network planning; distribution generation; niche technology; non- dominated-sorting; improved particle swarm algorithm

2018-05-30