塔式光热电站储热系统容量优化配置

毛维宙 陆华军 单宝奇



塔式光热电站储热系统容量优化配置

毛维宙1陆华军1单宝奇2

（1. 南京磐能电力科技股份有限公司，南京 210061；2. 河海大学能源与电气学院，南京 210098）

储热系统是塔式光热电站的重要组成部件，其容量大小一般用储热时间来描述。储热时间是储热系统所能储存的热量可以供汽轮发电机组在额定工况下运行的最大时间。目前已建的塔式光热电站的储热时间取值比较随意，未考虑其对电站经济效益的影响，本文提出了一种考虑综合经济效益对电站储热时间进行优化的方法，以在我国西部某地区建设50MW塔式光热电站为例，使用该地区的实际地理气象数据,建立了塔式光热电站的能量转换效率模型及经济性评价模型，以平准化度电成本最低为优化目标，分别得到了太阳倍数分别为1.8和2.4时电站的最优储热时间取值，分析了在一定太阳倍数下，储热系统容量对电站经济效益的影响，并分析了储热系统容量对电站年容量因子的影响。

塔式光热电站；储热系统；储热时间；平准化度电成本

目前，光热电站的形式主要包括槽式、塔式、线性菲涅尔式和碟式四种[1]。其中，塔式光热发电的聚光比较高，太阳能转化率高，发电效率提升空间更大，因此是最具有开发潜力的光热发电形式，也是大规模太阳能发电的最理想方式[2]。

目前国内外对于塔式光热电站储热系统的研究主要集中在储热系统结构设计、储热系统仿真等方面，而对储热系统容量优化的研究较少。文献[3]分析了目前储热系统的发展概况，比较了油盐和熔盐作为太阳能热电站的储热介质的经济性，得到了用来判断两者经济性优劣的比例曲线，并以50MW容量的太阳能热电站为例，建立了储热系统的经济性评价模型，通过模拟计算分析，对50MW电站的储热系统进行了优化设计，最终得出了储热系统的最佳结构。文献[4]介绍了储热系统设计方法的概况以及太阳能热电站储热系统设计时在不同层次上需要考虑的因素，讨论了储热系统设计以及应用到太阳能热电站中的各种储热系统的热能和效率分析。文献[5]开发了一种新的温跃层储热罐仿真模型，解决了以往文献中模型的不足，并将新的模型并入了一个100MW塔式太阳能热发电系统模型中，研究了温跃层储热罐长期运行期间的储热性能。

本文在建立塔式光热电站的能量转换效率模型及经济性评价模型的基础上，以平准化度电成本最低为优化目标，分别得到了太阳倍数分别为1.8和2.4时电站的最优储热时间取值。

1 塔式光热电站能量转换效率分析

1.1 塔式光热电站的组成及原理

通常，塔式光热电站主要由以下3个子系统组成：①聚光集热子系统，其作用是收集汇聚太阳能并将太阳能转化为传热介质的热能；②储热子系统，其作用是储存热能，供太阳能不足时发电使用；③热力发电子系统，其作用是将热能转化为电能，与常规发电相似。

塔式光热发电原理如下：利用大量独立跟踪太阳的定日镜，将太阳光线聚焦到一个固定在高塔顶端的吸热器上，加热其中的工质（熔融盐）产生高温介质，高温介质加热水产生过热蒸汽，带动汽轮机、发电机旋转发电[6]。塔式光热电站的实物图如图1所示。

图1 塔式光热电站实物图

下文通过分析各子系统的能量转换效率，建立塔式光热电站的能量转换效率模型。

1.2 定日镜场光学效率模型

1）定日镜效率组成

定日镜在工作时会受很多因素的影响，产生多种光学损失，使定日镜反射到吸热器的能量小于定日镜理论上能够接收的太阳能。定日镜场的这一特性可以用其光学效率来表达。定日镜场的总光学效率由单台定日镜光学效率综合得来，根据光学效率的影响因素，单台定日镜的光学效率包括余弦效率，大气透射效率，镜面反射效率，阴影和阻挡效率等。

若单台定日镜的面积为，则第台定日镜反射到吸热器入口处的能量P为式（1）。

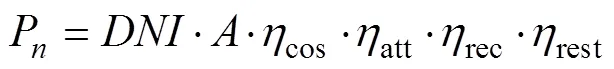
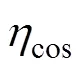
2）余弦效率计算

为使反射光线到达接收器，定日镜工作时，其表面不能总与太阳入射光保持垂直，而是呈现一个倾斜角。余弦损失就是因这种倾斜所导致的定日镜反射面面积相对于太阳光可见面积的减少而产生 的[7]。余弦效率可通过式（2）计算。

3）大气透射效率计算

定日镜场中任意一面定日镜的大气透射效率可通过式（3）[8]计算。

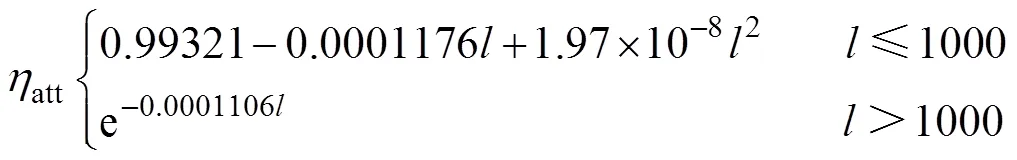
式中，为定日镜场中任意一面定日镜的镜面中心到吸热器中心的距离，m。

1.3 吸热器能量转换效率模型

1）吸热器的热损

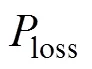
2）吸热器的反射热损

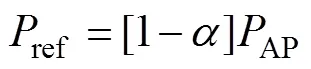
3）吸热器的辐射热损

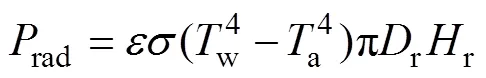
4）吸热器的对流热损

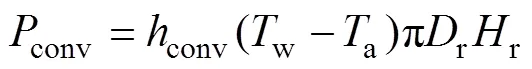
5）吸热器的热效率

由上可知，得到利用的有效热能，即

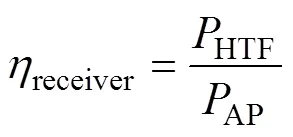
1.4 储热系统能量转换效率模型

1）充热效率

储热系统的充热效率定义为

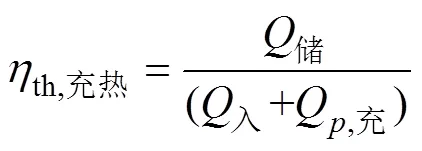
式（12）描述了从储存在高温熔盐罐中的热量相对于输入高温熔盐罐的热量和泵送能量的比。

2）放热效率

放热效率定义为

式（13）描述了从高温熔盐罐提取的热量相对于储存的能量和抽取所需的泵送能量的比。

3）整体效率

储热系统的整体热效率定义为

式（14）描述了用于单个充/放热循环的回收热量与输入热量和泵送能量的比。

1.5 热力发电系统能量转换效率模型

来自定日镜场或储热系统的能量进入热力发电系统转化为电能，这个过程的整体效率与负载水平呈非线性关系[11]。

文献[11]中的图3表示了热力发电系统效率与负载水平的函数关系，对其进行变换可得50MW塔式光热电站热力发电系统的整体效率与输入热量的函数关系，如图2所示。

图2 50MW塔式光热电站热力发电系统整体效率与输入热量关系图

2 塔式光热电站储热系统容量优化目标

2.1 太阳倍数和储热时间

太阳倍数和储热时间是影响塔式光热电站经济性评价的两个关键参数[12]。电站容量确定以后，太阳倍数和储热时间分别是镜场容量和储热系统容量的直接反映。因此，本文在对储热系统容量进行优化配置时，选择固定太阳倍数，调节储热时间，观察其对电站LCOE的影响，并以LCOE最低时的储热时间作为最优取值。

塔式光热电站储热系统的容量一般用储热时间来描述。储热时间是储热系统所能储存的最大热量可以供汽轮发电机组在额定工况下运行的时间。

2.2 平准化度电成本（LCOE）

LCOE是指当电站整个寿命周期内的总收益与总成本相等时的上网电价，也可理解为电站寿命周期内每发1kW·h电所需投资的成本。当电价高于此值时将产生更大的资本回报率，而低于此值时将会降低资本回报率甚至亏损。

LCOE是充分考虑了一座光热电站整个寿命周期内的投资，以及运行、维护、管理成本的一个综合性的参数，可根据式（15）计算[13]

塔式光热电站的成本计算数据[14-15]见表1。

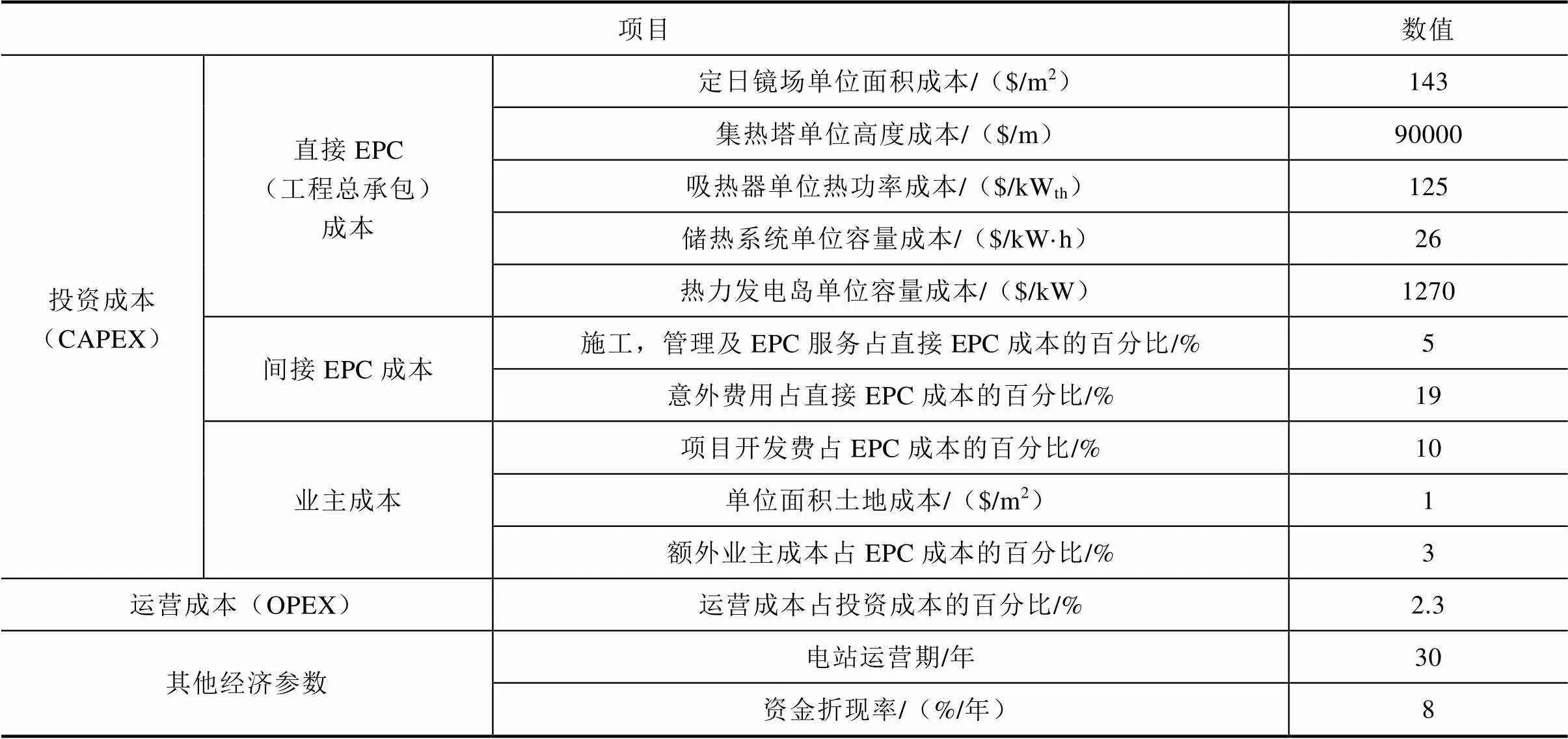
表1 塔式光热电站成本计算数据

本文年发电量计算采用基于逐时模拟的年发电量计算方法。该方法的要点是，根据一年内逐时的太阳辐照度数据，通过基于系统能量平衡的模拟来计算不同聚光场面积下的集热场输出与汽轮机额定输入之间的关系，以得到该汽轮机容量下的年最大发电量。

2.3 年容量因子

年容量因子是考虑光热电站年发电小时数的重要数据，也是电站年运行性能的反映。它是指电站实际年发电量与电站满负荷运行一年所发电量之比，可按照式（16）计算[16]。

3 模型验证

3.1 设计点参数选取

本文以在我国西部某地区建设50MW熔盐塔式光热电站为例建模，使用该地区的实际地理气象数据，并选择春分日正午12∶00的气象数据作为电站设计点参数，见表2。

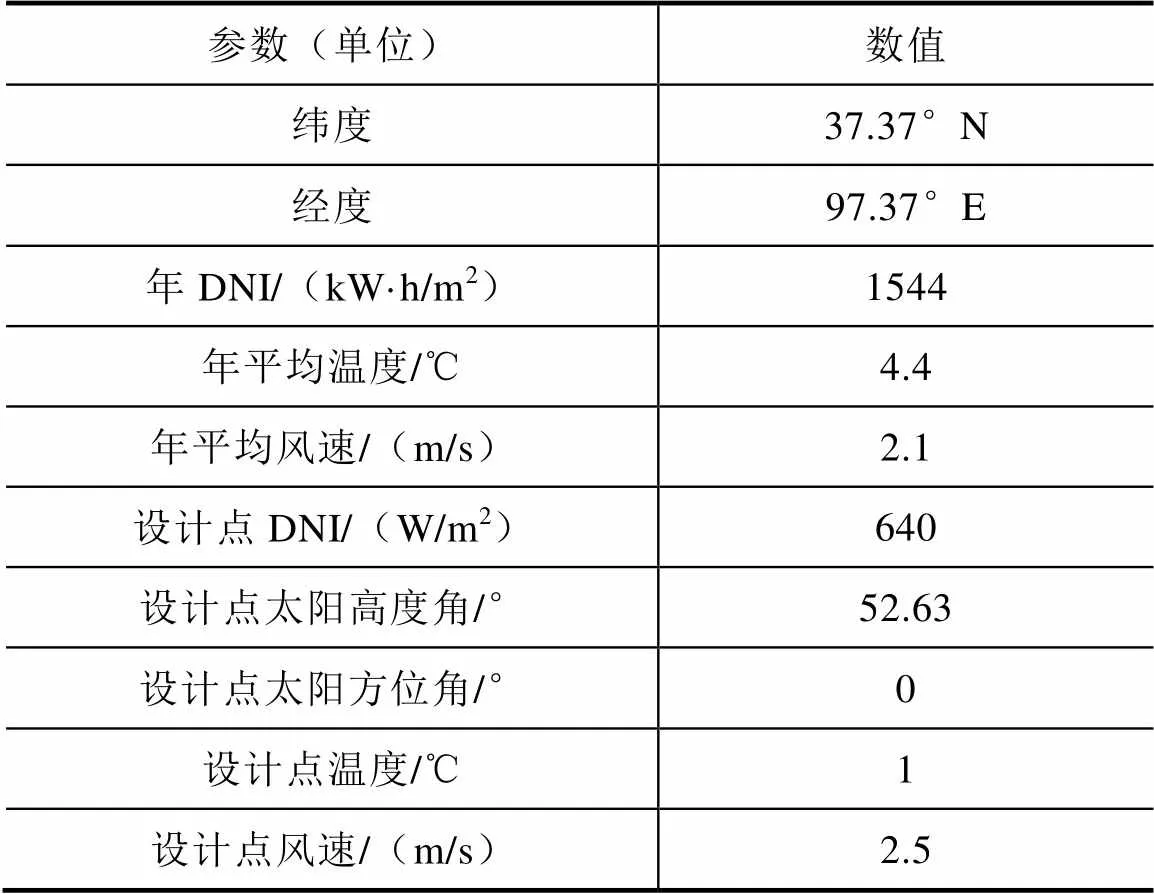
表2 我国西部某地区年地理气象数据及设计点参数表

3.2 储热系统容量优化配置

在以上设计点参数下，分别分析太阳倍数取1.8和2.4两种情况，储热时间分别取0～16h，间隔取2h，分析各个储热时间取值下电站LCOE的变化情况，得到电站综合经济效益随储热时间的变化规律，以最低LCOE为目标得到两种情况下储热时间的最佳取值。通过分析年容量因子的变化规律，得到储热时间对电站运行性能的影响。

1）LCOE分析

当太阳倍数分别被取1.8和2.4时，电站在各个储热时间取值下的LCOE分布分别如图3和图4所示。

由图3可以看出，当太阳倍数取1.8时，LCOE随储热时间先下降后上升，在储热时间取6h时，LCOE最低，为0.2113$/kW·h。这是由于，当储热时间小于6h时，定日镜场采集的太阳辐射能并未完全利用起来，定日镜场容量仍有一定裕量，此时如果增加储热时间，就能将定日镜场采集的多余太阳辐射能储存起来，供太阳辐射不足时发电使用，从而电站发电量能够随储热时间的增大而显著增加，因此LCOE会下降。当储热时间大于6h时，定日镜场采集的多余太阳辐射能已基本可以被储热系统全部吸收，此时即使继续增加储热时间，由于定日镜场能够采集的太阳能有限，电站的年发电量随储热时间的增加速率已十分缓慢，而电站投资仍然会随着储热时间的增加而大大增加，因此LCOE会随储热时间的增加而上升。

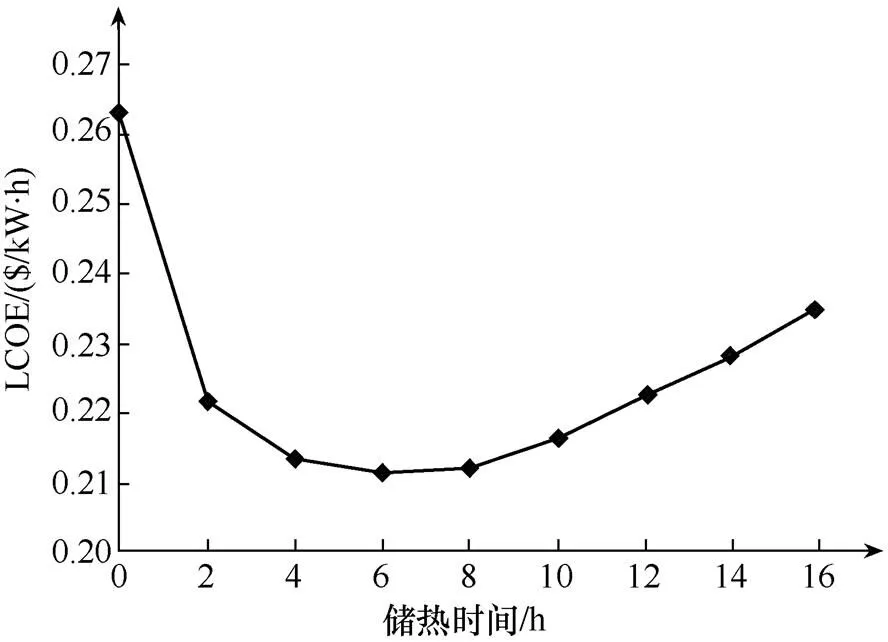
图3 太阳倍数为1.8时的LCOE分布图

图4 太阳倍数为2.4时的LCOE分布图

当太阳倍数取2.4时，LCOE随储热时间的变化规律与太阳倍数取1.8时类似，在储热时间取8h时，LCOE最低，为0.2049$/kW·h，如图4所示。

以上分析说明，太阳倍数为1.8时，储热时间取6h时电站的综合经济效益最优；太阳倍数为2.4时，储热时间取8h时电站的综合经济效益最优。

2）电站年容量因子分析

太阳倍数分别取1.8和2.4时，电站在各个储热时间取值下的年容量因子分布分别如图5和图6 所示。

由图5可以看出，随着储热时间从0～16h，电站的年容量因子从27.83%～39.74%。这是因为，储热时间越长，储热系统容量越大，储热系统能够储存的多余太阳辐射能越多，在太阳辐射不足时能够供给热力发电系统的热量越多，从而使发电时间增长，发电量增加，年容量因子增大。但是，由于太阳倍数已固定为1.8，定日镜场能够采集的太阳辐射能有限，当储热系统的容量已经足以将定日镜场采集的多余的太阳辐射能全部储存时，若继续增加储热时间，则增加的储热容量会被浪费，发电量不再增长，因此，年容量因子随储热时间的增长趋势不会一直持续，而是逐渐减缓，最终趋于一个最大值。

图5 太阳倍数为1.8时的年容量因子分布图

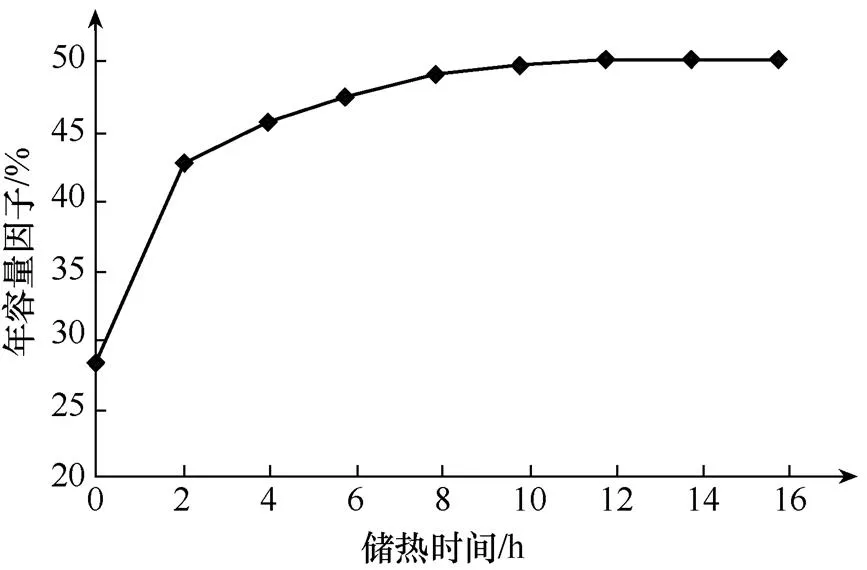
图6 太阳倍数为2.4时的年容量因子分布图

当太阳倍数取2.4时，年容量因子随储热时间的变化规律与太阳倍数取1.8时类似，如图6所示。

根据以上分析，年容量因子随储热时间的增加而增大。因此，增加储热时间有利于提高电站年发电量，提高电站的运行性能。但是，储热时间并不是可以无限制的增加，当储热系统足够将定日镜场采集的多余太阳辐射能储存时，继续增加储热时间反而会造成投资浪费。

4 结论

本文以在我国西部某地区建设50MW塔式光热电站为例，建立了电站的能量转换效率模型和经济性评价模型，研究了定太阳倍数下储热系统容量对电站运行性能及综合经济效益的影响，得到以下结论。

1）太阳倍数一定时，电站LCOE随太阳倍数的增大先下降后上升。

2）太阳倍数为1.8时，当储热时间取6h时电站的LCOE最低，经济效益最好。

3）太阳倍数为2.4时，当储热时间取8h时电站的LCOE最低，经济效益最好。

4）太阳倍数一定时，年容量因子随储热时间的增加而增大，但增长趋势会逐渐减缓，最终趋于一个最大值。

[1] 上海市建材科技情报研究所. 太阳能光热发电技术的发展[J]. 上海建材, 2017(1): 16-18.

[2] 彭玲玲. 走进太阳能发电新时代[J]. 中国科技奖励, 2011(10): 66-67.

[3] 张雅文. 太阳能电站双罐式熔盐蓄热系统的优化设计及研究[D]. 武汉: 华中科技大学, 2012.

[4] Kuravi S, Trahan J, Goswami D Y, et al. Thermal energy storage technologies and systems for con- centrating solar power plants[J]. Progress in Energy and Combustion Science, 2013, 39(4): 285-319.

[5] Flueckiger S M, Iverson B D, Garimella S V. System-level simulation of a solar power tower plant with thermocline thermal energy storage[J]. Applied Energy, 2014, 113(SI): 86-96.

[6] 黎韦偲, 马纪明. 塔式太阳能电站定日镜场的聚焦策略研究[J]. 可再生能源, 2016, 34(4): 475-480.

[7] 潘磊, 李丽娟, 丁婷婷. 塔式太阳能热发电镜场中余弦效率仿真研究[J]. 可再生能源, 2013, 31(2): 1-5.

[8] 贾亚晴. 塔式太阳能光热配套电站系统仿真研究[D].华北电力大学, 2015.

[9] Wu Shuangying, Xiao Lan, Cao Yiding, et al. Con- vection heat loss from cavity receiver in parabolic dish solar thermal power system: A review[J]. Solar Energy, 2010, 84(8): 1342-1355.

[10] Siebers D L, Kraabel J S. Estimating convective energy losses from solar central receivers[J]. Cavity Receivers, 1984.

[11] Usaola J. Operation of concentrating solar power plants with storage in spot electricity markets[J]. IET Renewable Power Generation, 2012, 6(1): 59-66.

[12] Jennie Jorgenson, Paul Denholm, Mark Mehos, et al. Estimating the performance and economic value of multiple concentrating solar power technologies in a production cost model[R]. Golden: National Rene- wable Energy Laboratory, 2013.

[13] Renewable energy technologies: cost analysis series[R]. International Renewable Energy Agency, 2012.

[14] Dieckmann S, Dersch J, Giuliano S, et al. LCOE reduction potential of parabolic trough and solar tower CSP technology until 2025[C]//Solarpaces Conference. AIP Publishing LLC, 2017.

[15] 李心, 赵晓辉, 李江烨, 等. 塔式太阳能热发电全寿命周期成本电价分析[J]. 电力系统自动化, 2015, 39(7): 84-88.

[16] Izquierdo S, Montañés C, Dopazo C, et al. Analysis of CSP plants for the definition of energy policies: The influence on electricity cost of solar multiples,capacity factors and energy storage[J]. Energy Policy, 2010, 38(10): 6215-6221.

Optimal allocation of thermal storage system capacity of solar power tower plant

Mao Weizhou1Lu Huajun1Shan Baoqi2

(1. Nanjing PANENG Technology Development Co., Ltd, Nanjing 210061;2. College of Energy and Electrica, Hohai University., Nanjing 210098)

Thermal storage system is an important component of solar power tower plant. Its capacity is generally described by thermal storage time. Thermal storage time is the maximum time that the thermal energy stored in the thermal storage system can be used for the operation of the steam turbine generator unit under rated condition. At present, the value of the thermal storage time of solar power tower plants that have been built is relatively arbitrary and its impact on the economic benefits of the power plant is not considered. This paper proposes a method for optimizing the thermal storage time of solar power tower plant considering the comprehensive economic benefits. We take the construction of 50MW solar power tower plant in a certain area of western China as an example. Using actual local geographic and meteorological data to establish the energy conversion efficiency model and economic evaluation model of solar power tower plant. The optimization objective is the minimum leveling cost of electricity. The optimal thermal storage time of the plant is obtained when the solar multiple is 1.8 and 2.4 respectively. And we analyzed the influence of the capacity of the thermal storage system on the economic benefit of the plant at certain solar multiple and the influence of thermal storage system capacity on annual capacity factor of power station.

solar power tower plant; thermal storage system; thermal storage time; leveling cost of electricity

2018-06-06

毛维宙（1990-），男，江苏省镇江市丹阳人，本科，助理工程师，主要从事继电保护及配电设备营销管理工作。