变异系数相似度在紧急群决策中的应用

北京信息科技大学 理学院，北京100192

一、引言

自然灾害事件，如地震和飓风等，常常会造成严重的后果，为了解决这种情况，管理部门需要采取应急计划和管理。也需要平时加强自然环境的治理，提高自然稳定性。随着经济、社会、自然条件的变化，管理决策的环境也变得日益复杂。

在决策过程中，需要考虑多方面的因素。王坚强等[1]提出了多属性群决策方法，基于算例分析验证所提多准则群决策方法的有效性与合理性。然而，相似性度量能够对两个事物之间相近程度进行综合评定。在实体人类学、数值分类学、生态学、信息检索、心理学、引文分析和自动分类等方面都使用了相似性度量[2]。其中，研究对象之间的相似性程度起到重要作用。在多准则群决策环境中，按各自的偏好对目标进行评价,从中寻求群满意目标或者排序。

Jaccard、Dice和余弦相似度经常被用来达到这个目的。Ye[3]用梯形模糊数的向量相似度，提出了一种多准则群决策方法，他延伸了Jaccard、Dice和余弦相似度。通过每一个方案和理想方案的权重相似度，可以得出所有方案的一个排序，然后找出最优方案。

本文以上述三种相似度为基础，提出一种新的变异系数相似度，并应用在紧急群决策中，研究结果表明，所提出的方法具有更好的相似性识别，适用于事件紧急群决策应用。

二、向量相似度

1、四种向量相似度的定义

定义1对于X=(x1,x2,…,xn)和Y=(y1,y2,…,yn)两个长度为n的向量（其中每一项都是正数），两个向量的Jaccard相似度定义如下[4]：

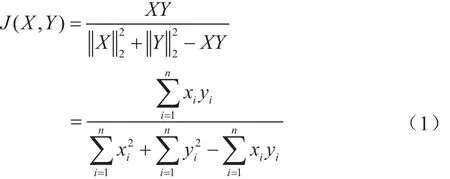
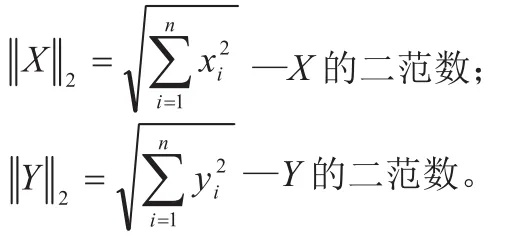
定义 2 对于X=(x1,x2,…,xn)和Y=(y1,y2,…,yn)两个长度为n的向量（其中每一项都是正数），两个相量的Dice相似度定义如下[5]：

定义 3对于X=(x1,x2, …,xn)和Y=(y1,y2,…,yn)两个长度为n的向量（其中每一项都是正数），两个相量的余弦相似度定义如下[6]：

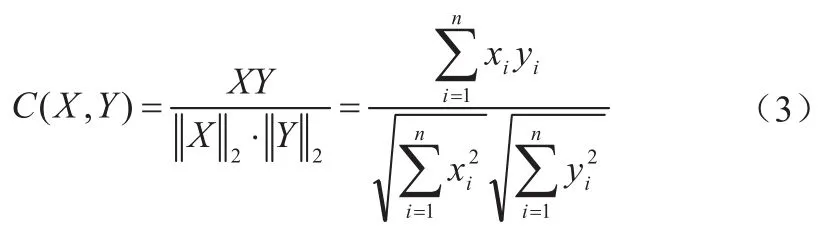
这三个公式是类似的，他们都在区间[0, 1]之间取值。但是上面三个定义都有一些缺点。对于所有的i(i=1,2,…,n)，xi=yi=0，Jaccard和Dice公式没有定义，对于所有的i(i=1,2,…,n)，xi=0或yi=0，余弦相似度公式没有定义。

根据这三个相似度的缺点，我们在定义4中定义了一种新的相似度——变异系数相似度。

定义 4 对于X=(x1,x2,…,xn)和Y=(y1,y2,…,yn)两个长度为n的向量（其中每一项都是正数），变异系数相似度定义如下[7]：

其中，α—变化的系数，且0≤α≤1。

在定理1中，我们需要证明向量X和向量Y之间的变异系数相似度满足下面一些特点。

定理1 令X=(x1,x2,…,xn)和Y=(y1,y2,…,yn)是两个长度为n的向量，变异系数相似度满足下面一些特点：

（P3）对于i=1, 2, …,n，如果X=Y，即xi=yi，则

（P1）证明：很明显V(X,Y)≥0，因此我们仅需要证明V(X,Y)≤1

又因为X和Y中每一项都是正数，所以XY≥0，且（θ为向量X与Y的夹角），有：

将（8）式代入（5）式得：

（P2）证明：由式（5）有：

（P3）证明：当X=Y，也即对于所有的i=1, 2,…,n，都有xi=yi成立，则由式（5）有：

由此，证明完毕。

2、不同相似度的比较

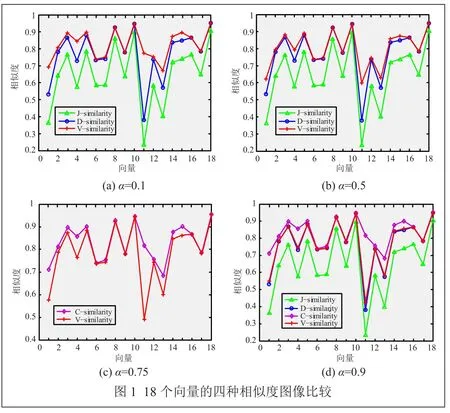
表1中列出了18个向量，并且偏序向量为a=[0.8542, 0.3460, 0.7000, 0.789, 0.1234, 0.6534]，令α=0.1，α=0.75，α=0.5和α=0.9，计算出这 18个向量和a的相似度[8]。

表1 群成员的偏序向量

图1对比了四种相似度图像。由图1(a)(b)(c)很容易看出，随着系数α变化，变异系数相似度（V-similarity）比 Jcaard相 似 度（J-similarity） 和Dice相似度（D-similarity）要好；由图1(c)(d)看出，余弦相似度（C-similarity）比其他三种相似度更好，但是在紧急群决策中它也存在一些问题，在下一部分将要介绍[9]。

三、紧急决策的应用

我们利用文献[10]中的例子，评估了湖南省部分县市的紧急管理能力。邀请了六个专家评估湘潭、娄底和郴州三个城市大雪灾的紧急管理能力，考虑了多个因素，汇总后得到六个一级指标：A1为投资总额、A2代表工程收益、A3是维护运行费、A4代表治理效果、A5是风险性、A6是对环境的影响。

提出的这种方法的决策过程可以概括如下：

步骤1：把文献[10]中4个方案的偏向量用下面这种方法进行标准化：

得到三个城市的偏向向量：湘潭（V1～V6）、娄底（V7～V12）和郴州（V13～V18），并在表 1 中列出；

步骤2：从六个专家可以看出，目标偏序向量是a=[0.8542, 0.346, 0.7, 0.789, 0.1234, 0.6534]。令α=0.75，由公式（4），得到18个向量Vi(i=1, 2,…,18)和目标偏序向量的相似度[11]；

步骤3：用18个向量和目标偏序向量的相似度，给出此方法的决策矩阵D=(dij)n×n和权重值：

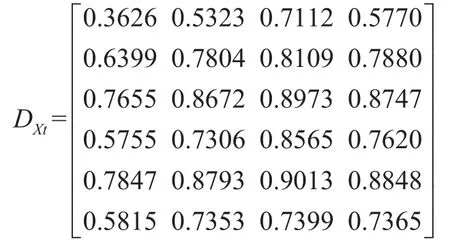
计算权重相似度，得到：

步骤4：用式（13）得到4种相似度的决策数值，列在表2中。为了作比较，系数为α=0.25时4种相似度列在表3中。

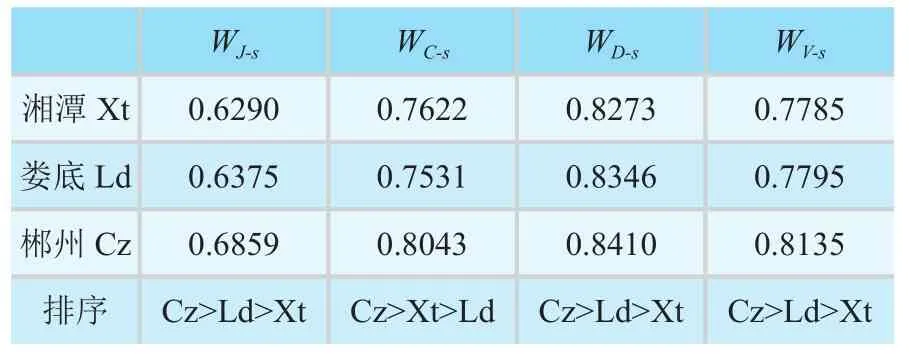
表2 当α=0.75时4种相似度的决策数值

表3 当α=0.25时，4个相似度的决策数值

从表2和表3中，可以看出来四个权重相似度WJ-s、WC-s、WE-s和WV-s的排列顺序，紧急管理能力最佳的地方是郴州[16]。

四、结束语

本文提出了一种变异系数相似度并且证明了它的一些特点，并将变异系数相似度和现存的相似度做了比较，显示了此方法具有更好的数值。这四个权重相似度被用来解决紧急群决策问题。最终，给出一个紧急能力评估的实际例子评估中国湖南三个城市的相似度能力。不同的相似度决策数值说明了可以得到三个城市的排序，并且紧急管理能力最佳的城市可以很容易得到，显示了本文提出的方法是合理和有效的。