非奇异M矩阵研究
张爱萍
(吕梁学院 汾阳师范分校数学与科学系,山西 汾阳 032200)
M矩阵是重要的特殊矩阵之一,它是瑞士数学家Ostrowski在1937年首次提出的术语[1],随后科学家和经济学家进一步发展了M矩阵的理论及应用[2].现在M矩阵在计算数学、经济学、生物科学、人工智能等很多领域都具有重要的应用[3].本文将重点研究非奇异M矩阵的一些重要特性.
1 M矩阵与非奇异M矩阵
定义1[4]设A∈Rn×n,并且可以表示为
A=sI-B,s>0,B≥0
(1)
若s≥ρ(B),则称A为M矩阵;s>ρ(B),则称A为非奇异M矩阵.

记
Zn×n={A=(aij)∈Rn×n|aij≤0(i,j=1,2,…,n,i≠j)}
(2)
2 有关非奇异M矩阵的主要结论
定理1[6]设A=(aij)∈Zn×n,为非奇异M矩阵,并且D∈Zn×n满足D≥A,则
①A-1与D-1存在,A-1≥D-1≥0;
②D的每一个实特征值为正数;
③det(D)≥det(A)>0.
证①由于A为非奇异M矩阵,因此有
A=sI-B,s>0,B≥0
(3)
对于任意实数ω≤0,考虑矩阵
C=A-ωI=(s-ω)I-B
(4)
由于s-ω>ρ(B),故C也为非奇异M矩阵.这说明非奇异M矩阵的每一个实特征值必为正数.由于D∈Zn×n,所以存在足够小的正数s,使得
P=I-εD≥0
(5)
由于D≥A,则得
Q=I-εA≥I-εD=P≥0
(6)
又由于ρ(Q)为Q的非负特征值,所以
det[(1-ρ(Q))I-εA]=det(Q-ρ(Q)I)=0
(7)
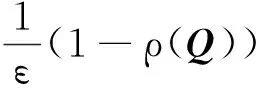
(I-Q)-1=(εA)-1=I+Q+Q2+…≥0
(8)
故有A-1≥0.由Q≥P≥0,可得
0≤Pk≤Qk,k=1,2,…
(9)
且有ρ(P)≤ρ(Q)<1,因此可得
(I-P)-1=(εD)-1=I+P+P2+…≤(εA)-1
(10)
从而得到A-1≥D-1≥0,即①得证.
②任取α≤0,则D-αI≥A,由①可得D-αI非奇异,因而D的所有实特征值为正数.从而②得证.
③通过以上分析,只需证明:如果A∈Zn×n的所有实特征值为正数,并且D∈Zn×n满足D≥A,则③成立.
实际上,对矩阵的阶数n应用归纳法.当n=1时,显然③是成立的.假设对k(1≤k (11) (A-1)m≥(D-1)m≥0 (12) 其中,(A-1)m表示A-1的(m,m)元素,即 (13) 因此,det(A)>0,det(D)>0,进一步利用归纳假设可得 det(D)≥det(A)det(D1)/det(A1)≥det(A)>0 (14) 定理2 设A=(aij)∈Zn×n,则下列8个命题是等价的 ①A为非奇异M矩阵; ②如果B∈Zn×n,并且B≥A,则B非奇异; ③A的任意主子矩阵的每一个实特征值为正数; ④A的所有主子式为正数; ⑤对于每个k(1≤k≤n),A的所有k阶主子式之和为正数; ⑥A的每一个实特征值为正数; ⑦存在A的一种分裂A=P-Q,使得P-1≥0,Q≥0,并且ρ(P-1Q)<1; ⑧A非奇异并且A-1≥0. 证由定理1很容易得到①⟹②. ②⟹③设Ak是A的任一k阶主子矩阵,K表示Ak在A中的行(列)序数集,λ是Ak的任一特征值.接下来使用反证法证明λ>0. 假设λ≤0.定义矩阵B=(bij)∈Zn×n,如下: (15) ③⟹④因为实方阵的复特征值成共轭对出现,所以实方阵所有的非实特征值的乘积为正数.由③可知,A的所有主子式为正数. ④⟹⑤显然成立. ⑤⟹⑥由于 det(A-λI)=(-λ)n+b1(-λ)n-1+…+bn (16) 其中,bk是A的所有k阶主子式之和.由⑤可知bk>0(k=1,2,…,n),故式(16)不可能有非正的实根,即A的每一个实特征值为正数. ⑥⟹①设A=sI-B,s>0并且B≥0,则s-ρ(B)为A的实特征值,⑥可知它为正数,即s>ρ(B).故A为非奇异M矩阵. ①⟹⑦取P=sI,Q=B,并且s,B满足 A=sI-B,s>ρ(B),B≥0 (17) ⑦⟹⑧由⑦可得A=P(I-C),其中C=P-1Q. 由于ρ(C)<1,有 A-1=(I-C)-1P-1=(I+C+C2+…)P-1 (18) 于是由C=P-1Q≥0,可得A-1≥0. ⑧⟹①记A-1=G=(gij),则由⑧可知G≥0.又由AG=I可得 (19) 因为aij≤0,gij≥0(i≠j),则有 (20) 由式(20)再结合gii≥0得 aii>0,gii>0,i=1,2,…,n (21) Ax=(s-ρ(B))x (22) 因为A是可逆的,所以s≠ρ(B).于是 (23) 由于A-1≥0,x≥0并且x≠0,所以s>ρ(B).因此A为非奇异M矩阵. 实际上,一般M矩阵与非奇异M矩阵在应用中几乎同等重要,下面再讨论一般M矩阵的一些特性. 定理3 设A=(aij)∈Zn×n,则下面几个命题彼此等价: ①A是M矩阵; ②对于每个ε>0,A+εI是非奇异M矩阵; ③A的任意主子矩阵的每一个实特征值非负; ④A的所有主子式非负; ⑤对于每个k(1≤k≤n),A的所有k阶主子式之和为非负实数; ⑥A的每个实特征值均非负. 证①⟹②由M矩阵的定义易证. ②⟹③设Ak为A的任一k阶主子矩阵,λ为Ak的任一实特征值.如果λ为负实数,由②可知B=A-λI也为非奇异M矩阵.再假设Bk是B的k阶主子矩阵,其行、列序号与Ak在A中的行、列序号相同.由定理2的④可得det(Bk)>0.因为λ为Ak的特征值,所以det(Bk)=det(Ak-λI)=0,但这与前述相矛盾.即③成立. ③⟹④由于A的主子式等于相应主子矩阵的所有特征值的乘积,而非实特征值之积为正数,实特征值之积为非负的,因此④成立. ④⟹⑤很明显成立. ⑤⟹⑥与定理2证明中⑤⟹⑥的证法相类似.因为 det(A-λI)=(-λ)n+b1(-λ)n-1+…+bn (24) 其中,bk为A的所有k阶主子式之和.由⑤可知bk≥0(k=1,2,…,n),那么式(24)不可能有负实根,即A的每个实特征值均是非负的. ⑥⟹①用与定理2中证明⑥⟹①相类似的方法即可证得.



3 有关一般M矩阵的主要结论

