基于D-PMSG的风火打捆直流外送系统送端功角暂态稳定性研究*

米合丽班·阿不都哈力里，王维庆，王海云

(新疆大学 电气工程学院 教育部可再生能源发电与并网控制工程技术研究中心, 乌鲁木齐 830047)

0 引 言

日益严重的环境污染问题不断地提醒我们发展可再生能源的重要性。风力发电是最具规模化开发条件的可再生能源利用技术之一[1]。截至2016年底，我国风电新增装机容量2 337万kW, 占全球新增装机容量的42.7% 。目前，我国东北、华北、西北等部分地区的风能资源和煤炭资源存在能源就地消纳不完的问题，两种能源均需要大规模集中接入、远距离输送至东部和中部负荷中心。随着直驱永磁风电机组并网容量的不断增大，研究直驱永磁风电机组与火电机组打捆直流外送系统送端功角暂态稳定性意义重大。

分析电力系统暂态稳定性的方法主要有时域仿真法和直接法[2-3]。风火打捆并网方式对系统稳定的影响主要体现在风功率的波动和不同发电机组的电源特性。文献[3-4]针对双馈风机推出其等效模型，分析了双馈风机的接入对系统功角暂态稳定性的影响。文献[5]定义了双馈电机的功角快变特性，并分析了此特性和双馈电机的机械转动惯量对“风火打捆”系统火电机组功角暂态稳定性的影响。文献[6]研究了风电机组类型和输出功率比例的不同对系统送端暂态稳定性的影响,并得出结论为双馈风力发电机与火电机组打捆系统暂态稳定性优于其它类型风力机。文献[7]分析了双馈风力发电机组的功率特性，研究了系统送端风火互替对于系统功角稳定性的影响。文献[8]将风电场电磁功率与机械功率等值为同步发电机的机械功率的增量，通过EEAC(扩展等面积法则)对其含风电场的电力系统进行了稳定判断，文献[9]在此基础上推导了系统功角加速度与风电比例之间的关系，针对系统余下群为无穷大系统和非无穷大系统两种情况进行讨论分析，总结出了风电比例影响临界群与余下群相对功角首摆稳定性的规律。文献[10]探讨了风电、火电和直流系统间的相互作用，分析了不同风电比例和不同直流控制方式下系统的功角暂态稳定特性。文献[11]在最基本的风火打捆交直流外送系统模型的基础上，仔细探究了系统送端直流线路发生故障时的暂态稳定性，分析了不同风火配比、不同容量的换流器、不同直流控制方式对暂态稳定性的影响。文献[12]建立了D-PMSG的完整模型和两种等效模型，并比较不同模型的接入和不同控制方式对系统暂态稳定性的影响。

综上所述，目前，风火打捆外送系统功角暂态稳定性的相关研究主要针对风火配比，风电、火电、直流系统间的相互作用等方面，且其模型为基于双馈型风电机组的风火打捆外送系统模型，但是对基于直驱永磁同步风力发电机的风火打捆外送系统的功角暂态稳定性研究很少。文章从这一点出发，以上述的研究思路为基础，研究了基于直驱永磁风力发电机的风火打捆直流外送系统的功角暂态稳定性。

1 风火打捆直流外送系统结构

1.1 风火打捆直流外送系统

风电并网后系统是否能够保持在稳定运行状态与风速相关，风功率的随机波动会使系统偏离稳定运行状态。尽管系统的安全稳定的运行能力可以通过适当的方法维持，可是还是不能够从根本上解决。采用风电与附近火电打捆经特高压直流外送的方式，不仅可以满足可再生能源和大规模传统能源外送的基本要求，而且可以保证特高压直流输电通道输送功率的平稳，有效提高直流系统的利用率[11]。

文中风火打捆系统与受端交流电网经HVDC系统相连，送端由火电厂和基于D-PMSG的风电场构成，系统结构如图1所示。

图1 风火打捆直流外送系统

1.2 风电机组模型

直驱永磁风力发电机模型由风速模型、风轮模型、发电机模型、逆变器、保护系统模型以及相应的各控制器模型组成。该系统中风力机与永磁同步发电机直接联在轴系上，中间无齿轮箱，而永磁同步发电机通过全功率变换器和升压变压器并到网上。全功率变换器使风电机组和电网二者频率得到匹配的同时还可以使二者隔离，可以起到抑制或减小扰动的作用。因为电机与电网完全解耦，所以不是电机而是逆变器产生并入电网的无功功率。直驱永磁风力发电机模型如图2所示。

图2 直驱永磁风力发电机模型

1.3 直流系统模型

特高压直流一次系统选用准稳态模型，T 型等值电路模型表示直流线路及平波电抗器，代数方程表示直流换相过程、将代数方程与微分方程合并消元，可以得到式(1)所示的UHVDC数学模型：

(1)

式中Idr、Idi、Vc为状态变量；Idr和Idi分别为整流侧和逆变侧直流电流；Vc为直流线路中点电压；Rd为直流电阻；Cdc为直流线路对地等值电容；Udr和Udi分别为整流侧和逆变侧直流电压；LdrΣ和LdiΣ分别为整流侧和逆变侧等效电感；Xr和Xi分别为整流侧和逆变侧的换流电抗；α和β分别为整流侧触发延迟角和逆变侧触发越前角。

2 D-PMSG功角特性

D-PMSG矢量图如图3所示。图中，E与Us分别为等效内电势与机端电压;δ为D-PMSG等效功角。如果输入的机械功率增加，也就是说功角增大，输出的电功率随着增大，当δ=90°时电功率达到最大值。结合此功角特性，D-PMSG的功率输出可写为：

(2)

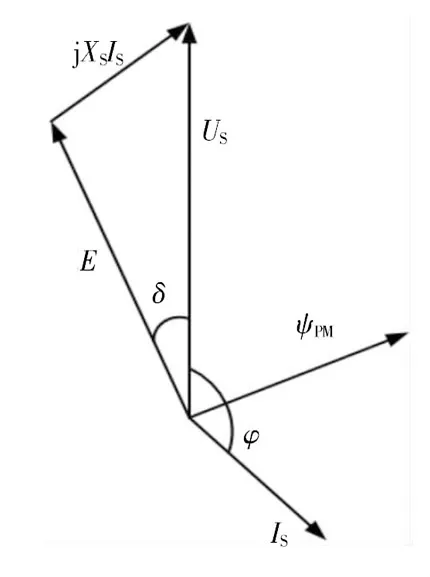
图3 D-PMSG矢量图

D-PMSG输出的有功功率与无功功率因中间的变频器环节被解耦，正常运行时功率因数为1，即无功功率为0。当电力系统发生故障时，D-PMSG机端电压会跌落，有功功率和无功功率也会偏离其正常范围。故障清除后，D-PMSG又快速恢复到恒功率因数运行方式。

3 D-PMSG的接入与HVDC输电方式对火电的影响

3.1 D-PMSG的接入对火电的影响

D-PMSG的接入使系统变为包含两种同步发电机的模式，一种是常规同步发电机，另一种是D-PMSG。但是D-PMSG因中间的全功率变频器与电网隔离，与常规同步发电机不是同步运行。因此风火打捆系统送端功角稳定性问题转变为分析D-PMSG接入后常规火电机组的功角稳定性问题。假设不考虑风电时系统失稳模式为双机模式，MS和MA分别为受扰严重群惯性时间常数和余下群惯性时间常数，δS和δA分别对应其功角。两机系统映射到单机无穷大系统后等值运动方程为：

δ=δS-δA

(3)

(4)

(5)

(6)

(7)

(8)

式中Pmi和Pmj分别为第i台和第j台同步发电机的机械功率；Pei和Pej为第i台和第j台同步发电机的电磁功率；Pm和Pe为单机无穷大系统等值机械功率和等值电磁功率；M与分别为等值惯性时间常数和等值功角加速度。考虑风电时，设定负荷与风速不变，风火打捆系统D-PMSG输入的功率由S机群减机械功率来平衡。

(9)

(10)

式中 功率符号下标1和0分别对应于风火打捆系统和纯火电系统。整理式(7)～ 式(10)可得风火打捆系统等值机械功率，即：

(11)

由上式可知，D-PMSG接入后风火打捆系统的机械功率相对纯火电系统的下降，使得稳定运行点也下降。受扰前后，风火打捆系统等值电磁功率与纯火电系统的一致。在受扰期间，D-PMSG输出较大的有功电流，但是因为全功率变频器的限流作用，其有功电流增大的幅度受限，使电磁功率曲线下降。比起等值机械功率，等值电磁功率的下降幅度较小，导致受扰期间风火打捆系统等值加速功率△P1小于纯火电系统等值加速功率△P0。由式(6)可知，受扰期间风火打捆系统等值功角变化得也小，即：

δτ1-δB1<δτ0-δB0

(12)

式中 下标B表示扰动前，根据式(12)，又有δB1<δB0，可推出风火打捆系统在扰动消除时具有较小的功角，即δτ1<δτ0。

图4 风火打捆系统与纯火电系统等值功角对比

图4中，直线阴影部分表示纯火电系统，斜线阴影部分表示风火打捆系统。可见，D-PMSG接入后风火打捆系统的加速面积减小，减速面积增大，通过扩展等面积准则可判断系统功角暂态稳定性变好。

3.2 HVDC输电方式对暂态稳定的影响

系统受扰时，直流输电线路输送功率几乎降为零，扰动消除后功率恢复比较快。按直流线路的特性来分析，它对系统起阻尼的效果，使得系统等值机械功率下降，相对纯交流输电方式减速面积增大，有利于系统的暂态稳定性。

4 仿真

在DIgSILENT/Power Factory仿真平台中搭建风火打捆经超高压直流外送系统仿真模型。送端风电场由单机容量为1.5 MW的120台D-PMSG组成，输出的总有功功率为180 MW。常规火电厂设计输出总有功功率为672 MW，由4台单机容量210 MVA的火电机组构成，其功率因数为0.8。

三相故障短路设置在风火打捆高压直流外送系统送端BUS1母线侧，即在3 s时发生，0.2 s后故障切除，30 s后停止仿真。系统火电厂功角曲线如图5所示。

图5 三相短路情况下火电厂功角波动

由图5(a)可知，风火打捆系统和纯火电系统送端遭受到三相短路扰动后，火电厂功角有明显的波动，其中风火打捆系统火电厂功角最高达到105.3°，最低降至 -16.7°；把风电场替换成等容量的火电厂后，系统变为纯火电系统，其功角最高达到107.9°，最低降至 -19°；故障清除后功角波动逐渐变小，最终恢复到原来的稳定状态，可以看出，风火打捆系统恢复稳定状态所耗的时间比纯火电系统耗的短。由图5(b)可知，当风火打捆系统经交流输电线路输送电能时，火电厂功角最高达到135°，最低降至 -24.8°；可以看出，虽然交流输电方式扰动清除后也能恢到原来的稳定状态，但是受扰时功角波动大于直流输电方式，且恢复稳定状态所耗的时间也比直流输电方式的长。

5 结束语

探讨了由直驱永磁风力发电机构成的风电场和附近火电厂打捆，经直流线路外送系统的送端功角暂态稳定性。通过理论与仿真分析系统送端侧发生三相短路故障可以得出：(1)当风火打捆系统中D-PMSG输入的功率由受扰严重群减机械功率来平衡的情况下，其功角暂态稳定性比纯火电系统的好；(2)风火打捆系统经直流线路输送电能时的功角暂态稳定性比经交流线路输送电能时的好。仿真结果与理论分析结果一致，可以说由D-PMSG构成的风电场与附近火电厂打捆，经直流线路外送的方案可以提高系统的功角暂态稳定性。