设置逆向可变车道的交叉口信号配时优化研究

刘 怡，常玉林,毛少东

(1.江苏大学 汽车与交通工程学院， 江苏 镇江 212013； 2.无锡市政设计研究院有限公司， 江苏 无锡 214072)

可变车道是指功能随交通流特性的变化而变化的车道，可将轻交通流方向的闲置空间资源分配给重交通流方向，从而达到缓解交通拥堵的目的[1]。国内外专家学者针对可变车道的设置进行了多方面深入研究，收获颇多[2-8]。近年来，学者们重点研究适应逆向可变车道的信号配时方案。刘伟等[9]提出以延误最小、通行能力最大为目标的双目标函数控制模型，得到逆向可变车道的信号配时方向；赵靖等[10]针对较大左转车流提出EXIT Lanes For Left-turn设计，其设计思想与逆向可变车道一致。魏家蓉等[11]以环境效益为目标，考虑油耗和排放费用，兼顾道路延误，得到可变车道的方案选择模型。魏依[12]从可变车道的设置条件和信号配时方法两方面研究了主干路可变车道的设置方法。姚荣涵等[13]提出具有可变导向车道的交叉口时空资源优化模型以及可变导向车道标志与信号灯组协调控制方法，并通过仿真验证了模型的有效性。逆向可变车道是可变车道理论的一种延续。逆向可变车道的概念：设置在信号交叉口出口道内侧，车道功能随交通信号周期性变化，既可以作为出口道行车道，又可以作为进口道左转车道。由于该车道在出口道设置为逆向车道，随信号相位而具有不同的功能定位，故将该车道定义为逆向可变车道。

2013年济南市交警技术部门为了缓解经十路交通拥堵，提出利用借道左转的逆向可变车道技术，设置逆向可变车道后左转车辆通行效率提升近50%[14]。逆向可变车道技术使交通组织技术向精细化发展又前进一大步。但采用逆向可变车道技术的城市屈指可数，究其原因是缺乏相应的实施技术标准，因此论文针对设置逆向可变车道的交叉口信号配时进行研究，得到相关配时技术参数和数学模型，为逆向可变车道技术在全国范围内的推广提供技术借鉴。

1 交通流特性研究

1.1 数据采集

选取经十路舜耕路交叉口进行数据采集，抽样调查，调查时段选取早高峰7∶00—9∶00和晚高峰17∶00—19∶00。以5 s为时间间隔，分别统计各时间间隔的交通量(折算为标准车)，进一步处理得到各时间间隔的消散流率，连续统计1 h，再对各周期同时间间隔的消散流率取平均值，即可得到绿灯期间各时间间隔的平均消散流率[15]。表1和表2是通过调查得到的经十路舜耕路交叉口车道参数和信号配时参数。

表1 经十路舜耕路交叉口车道参数

表2 经十路舜耕路交叉口信号配时参数

1.2 实际流率特性研究

饱和流率是绿灯开启后，排队车辆连续释放达到的最大流率。设置逆行可变车道的信号交叉口，左转车辆排队空间变为前端2个车道末尾一个车道，排队空间发生变化，饱和流率持续时间也会受影响，此时设置合理的绿信比将有效弥补空间变化的影响。下面首先通过实际调查数据的处理，分析设置可变车道的交叉口流率特性。

如图1所示，可变车道和左转专用车道的交通流率都在第2个5 s接近饱和流率，而且饱和流率阶段曲线趋势相似，根据驾驶员行为选择特性，可以较理性化认为可变车道和专左车道是1∶1释放车辆；东、西进口可变车道饱和流率分别持续15 s、25 s左右。如图2所示，4个进口道左转车流流率波动性最小的是西进口道，饱和流率持续时间最长，东进口可变车道最短，左转车流流率波动性最大；北进口道波动性介于东、西进口左转车流流率波动性之间。

图1 可变车道和左转专用车道的实际流率

图2 4个进口左转流率

如图3所示，设置逆向可变车道后，直行车道1(与左转车道相邻)与直行车道2(与直行车道1相邻)流率特性差别不大，基本是在第2个5 s接近饱和流率，数据表明逆向可变车道对直行车辆影响很小。

图3 直行车道实际流率

综合上述，得到以下对比分析结果：

1) 不论是左转还是直行车道，流率基本在第2个5 s接近饱和流率。逆向可变车道排队、释放过程轨迹与左转专用车道基本相同。

2) 可变车道长度对左转饱和流率的变化影响显著，可变长度越长，饱和流率持续时间越长。

2 信号配时参数优化

2.1 可变车道预信号配时

逆向可变车道采用“先左转再直行”相序。逆向可变车道的预信号配时2个重要的参数是延迟开启最小时间和提前关闭最小时间。延迟开启最小时间研究针对的是逆向可变车道待行区功能最大化，提前关闭最小时间研究针对的是逆向可变车道的左转车道功能最大化。

2.1.1 延迟开启最小时间

可变车道在相交方向直行相位时开启，理论上直行绿灯亮起，左转可变车道绿灯亮起，实际上开启时间不能太早，否则进入可变车道的车辆会与相交方向左转车辆冲突。

如图4所示，可变车道延迟开启时间即车辆B从P1点到冲突点P4的行驶时间，可分为3部分，分别是P1P2、P2P3和P3P4。P1P2为南北方向左转相位黄灯扫尾期间，记为Tp1p2；P2P3为车辆B沿弧线行驶，以稳定速度vl进入出口道，记为Tp2p3；P3P4为车辆B进入出口道可变车道后，加速行驶至交叉口限行速度，然后再以限行速度匀速驶离，记为Tp3p4。故车辆B从直行绿灯亮起到驶离冲突点P4的最大行驶时间，即可变车道的延迟开启最小时间td，min需满足：

(1)

图4 交叉口相位转换过程车辆极限行驶状态

2.1.2 提前关闭最小时间

逆向可变车道作为左转车道时，车辆要经过2次信号指示，预信号与路口的主信号协调配合要保证绿灯末尾到达车辆能连续通过预信号和主信号，关闭过早或过晚都会影响交叉口的通行能力。因此预信号要比主信号提前时间ta，min，即：

(2)

2.2 信号周期及绿信比

信号配时的关键是确定周期和绿信比。周期大小直接影响交叉口通行能力、车辆平均延误等，绿信比反映交叉口各相位绿灯时长的大小[16]。以设置逆向可变车道的流率时变规律为依据，对Webster最佳周期及绿信比算法进行改进。以典型四相位交叉口作为交通背景，对周期及绿信比参数进行分析。

(3)

理论上直行交通流率的变化主要经历3个阶段：绿灯启亮后，排队首车经过反应延迟后启动并加速驶离停车线，通过几辆车以后流率达到饱和流率状态并稳定持续一段时间，流率开始下降，直至降为到达流率并持续至绿灯结束，流率下降为0。直行相位绿灯期间各阶段流率消散模型如下：

(4)

式中：nsf为直行车辆数期望值(veh)；gsf为持续时间(s)；rs为直行红灯时长(s)；qs为直行车辆到达流率(veh/s)；Sij为直行相位各阶段消散流率(veh/h)，i=2,4，j=1,2,3；gij为直行相位各阶段消散流率持续时间(s)，i=2,4，j=1,2,3；gi为直行相位绿灯时间(s)，i=2,4；ri为直行相位红灯时间(s)，i=2,4。

ri计算方法如下：

ri=c-gi，i=1,2,3,4

(5)

各相位到达流率与消散流率比值如下：

，i=1,2,3,4

(6)

式中：yi为到达流率与消散流率比，i=1,2,3,4。

其次，行政执法行为不规范。行政机关囿于执法能力、执法水平之限，行政执法可谓“简单、粗暴、高效率”。而行政执法不仅要注重法律效果，更要注重社会效果，殊不知采取劝解、说理的柔性执法方式解决执法纠纷更能够取得良好的社会效果。为达到“高效率”的执法目标，显示执法的“果断、迅速”，部分执法机关草率调集武力维稳，须知滥权违法执法只会加剧事态恶化。

周期仍为Webster的最佳周期确定方法：

(7)

根据等饱和度分配原则，绿灯时间如下：

，i=1,2,3,4

(8)

交叉口设计配时之前首先要做交通调查，各阶段消散流率值可由交通调查获取，由式(3)～(8)可得到关于未知变量c、gi、vi(i=1,2,3,4)的9组方程，通过计算机智能算法，解方程组得到c、gi的具体值，即为相关信号配时参数。

3 实例分析

3.1 模型计算

以济南市经十路舜耕路交叉口为交通背景，根据实际调查数据，选取了晚高峰17∶30—18∶30的交通量数据，见表3。

根据表3所示，得到可变车道预信号配时参数以及交叉口主信号配时参数评价，见表4和表5。

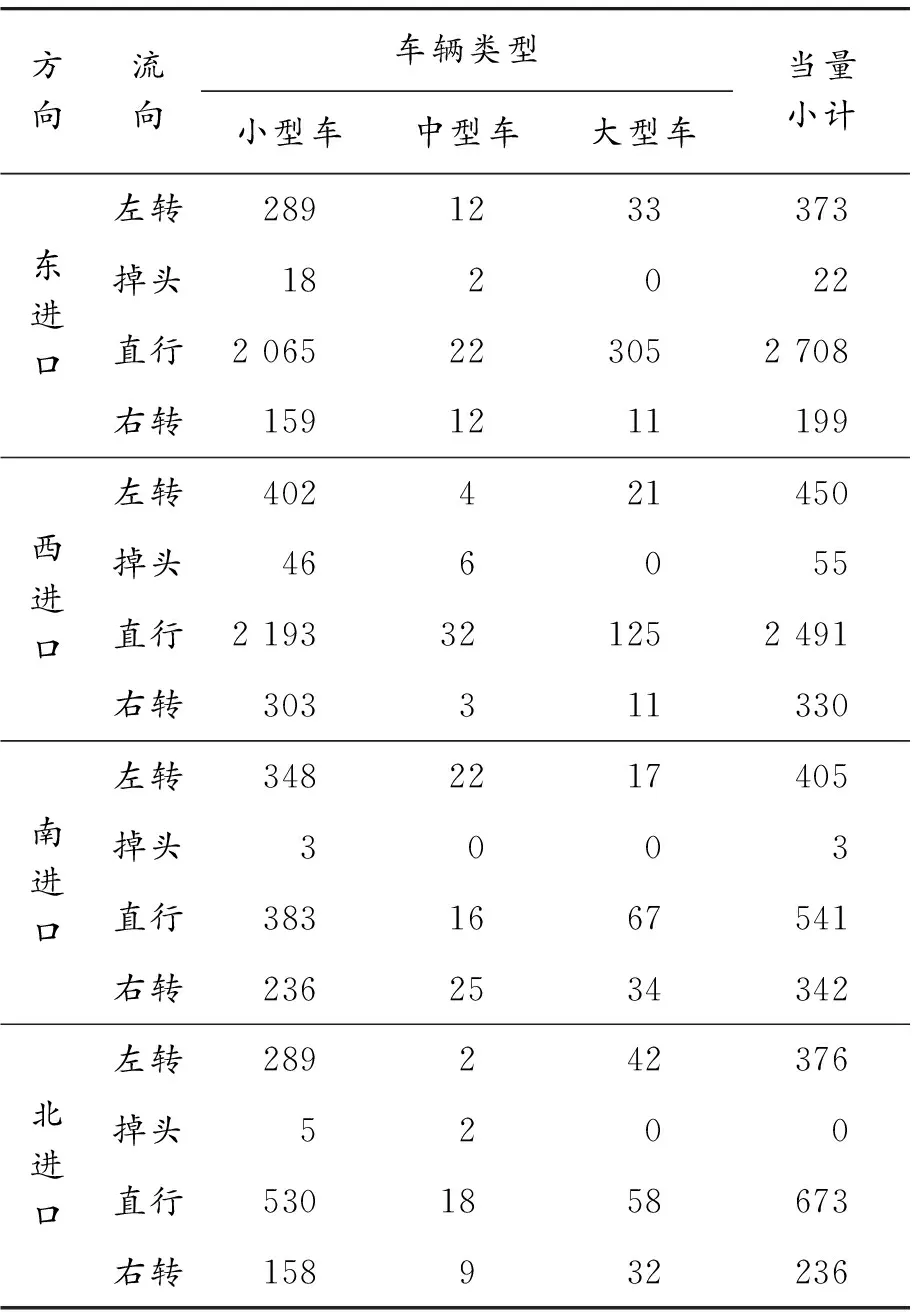
表3 晚高峰交通量数据 (veh·h-1)

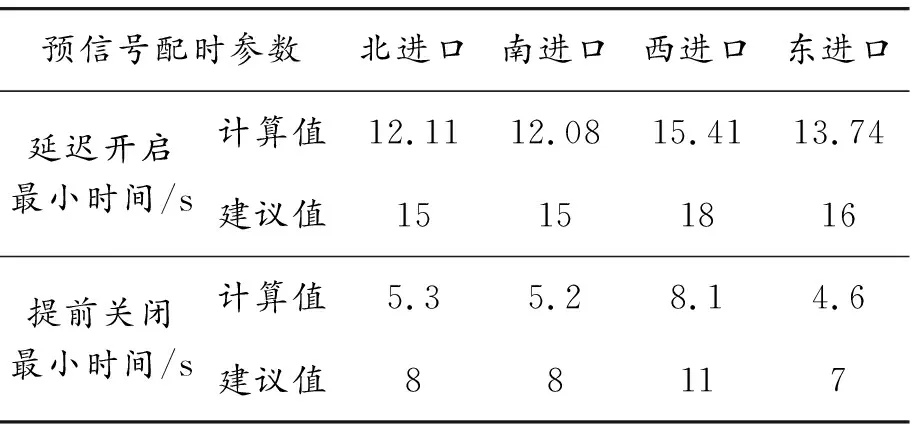
表4 可变车道预信号配时参数

表5 交叉口主信号配时参数评价

由表5得到，现状配时方案信号周期比改进的Webster配时方案得到的最佳周期大不少，通行能力仅提高了4.91%，但计算得到的平均延误时间却比改进的Webster配时方案大了21.9%，很明显改进的Webster配时方案的配时效果更佳。

3.2 仿真验证

为了验证改进的Webster配时方案的有效性，以经十路舜耕路交叉口作为交通背景，采用Vissim 4.3仿真软件进行模拟验证。

1) 仿真软件基本参数

车辆构成：全部由小汽车构成，仿真车辆也采用当量交通量。期望车速：50 km/h。车辆参数：车辆长4.11～4.76 m，平均停车间距3.5 m，平均车头间距约8 m。仿真时间：4 800 s。数据采集时间为1 200～4 800 s。

2) 仿真结果分析

将Vissim仿真结果与模型计算结果进行对比分析，对比数据见表6。

表6 Vissim仿真与模型计算对比数据

仿真结果显示：现状信号配时方案和改进的Webster配时方案的仿真结果与计算结果相对误差都在10%左右，可以表明仿真的有效性。仿真得到现状配时的通行能力仅比改进的Webster配时方案高4.3%，但平均延误时间却高了26.1%，与模型计算结果基本吻合。仿真结果与模型计算对比分析得到：改进的Webster配时模型可有效适应设置逆向可变车道的信号交叉口配时。

4 结束语

本文首先以实际交通调查数据为基础，研究设置逆向可变车道对饱和流率的影响，并通过定量分析左转车道与直行车道设置逆向可变车道的交通流变化，验证了可变车道长度对左转交通流率的显著影响。

通过建立分阶段消散流率模型，优化相位相序，建立可变车道预信号配时参数模型，在确定相位相序和可变车道预信号配时参数的基础上依据流率时变规律，对Webster最佳周期及绿信比算法进行修正。

以济南市经十路舜耕路交叉口为交通背景，利用Vissim软件仿真验证改进的Webster配时模型有效适应设置逆向可变车道的信号交叉口配时。

由于逆向可变车道设置研究需要大量的调查数据，但是实施逆向可变车道的城市非常少，所以调查数据有限，会对本文的研究结论产生一定影响。

本文对可变车道开口掉头车辆没有做研究，下一步将针对中央分隔带开口处进行交通数据采集，研究掉头车辆对通行能力、延误的影响。