下游停靠站影响的交叉口公交优先配时优化

诸葛雪玉

(河海大学土木与交通学院，江苏 南京 210098)

1 概述

陈群和晏克非考虑公交优先，并从我国城市交叉口的交通特征出发对城市交叉口信号配时作了研究[1]。路庆昌等从交叉口的总体效益出发，以乘客人均延误最小为目标，以饱和度、短周期、最小绿灯时间为约束条件，提出了公交优先周期优化模型[2]；Li等人针对乘客延误和延误离散程度，制定了信号协调控制方法，并对交叉口信号配时进行优化，并采用VISSIM仿真验证了模型的可行性[3]。吴志周等人在固定式信号配时方案下，以车均延误为优化目标，建立了停靠站最佳布置位置的选择模型，并对交叉口和停靠站的组合进行实例计算分析，得出信号协调控制方案下的停靠站最佳布置方案，降低了车辆延误，并且通过VISSIM仿真验证了模型计算结果[4]。

虽然在交叉口处对公交车辆实施信号优先，但是由于交叉口通行特征复杂，特别是很多停靠站也设置在交叉口进出口道上，这些停靠站(尤其是交叉口下游公交停靠站)将会限制交叉口公交通行效率。如果上一相位的公交车辆未能在下游停靠站利用本周期的红灯时间完成乘客上下客服务，绿灯启亮后，新的公交车辆到达停靠站后需要排队等待进行服务,严重时影响社会车辆进入交叉口。这在极大程度上降低了交叉口的通行效率，增加了公交停靠站的乘客候车时间。更重要的是，严重影响了公交车辆的服务水平与准点率。因此需要从停靠站的角度出发，重点分析下游站点对交叉口交通的影响，研究公交优先信号配时方法。

2 公交信号配时优化模型建立

在下游公交溢出影响研究基础上，假设只有一个进口道设置停靠站的交叉口进行公交信号配时优化。以交叉口的人总延误最小为优化目标，以避免相位过饱和和最小绿灯时间为约束条件，建立信号配时优化模型，调整公交优先相位的绿灯时间。

目标函数为：

(1)

式中：D——交叉口人总延误；

Pt——公交车平均载客量,per；

ds——站点公交乘客延误；

xij——相位i的j进口方向饱和度；

λi——i相位绿信比；

C——周期长度,s；

gmini——i相位对应的最小绿灯时间,s。

对社会车和公交车的平均延误采用韦伯斯特延误模型，则有：

(2)

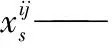
3 实例分析验证

3.1 交叉口交通条件

选取江东北路—清凉门大街交叉路口作为仿真对象。如图1所示为实验路段的交叉口布局以及相位设置情况。江东北路—清凉门交叉路口为四相位的十字交叉口，东、西、南、北四个进口道各自设有5条车道，分别为1条右转车道、2条直行车道以及2条右转车道。其中南北进口道最右侧的直行车道均为公交专用道。本实验选取的公交停靠站为南进口道对应的下游停靠站，此停靠站设有7条公交线路。

对交叉口工作日晚高峰(17:00 PM～18:00 PM)进行交通量调查，流量数据如表1所示。

表1 交叉口交通流特性表

通过统计得到不同线路公交车在站平均消耗时间及乘客占有率，如表2所示。

表2 不同线路公交车平均在站消耗时间及乘客占有率

图2为该交叉口原始信号配时方案，其中公交相位与南北进口道直行相位属同一相位。因为四个进口道的右转方向均设有右转专用道与右转专用相位，所以忽略右转方向。

3.2 信号配时优化

南北直行相位为本研究的优化相位，根据HCM2000推荐得到交叉口的饱和流率为1 700 pcu/h/l，公交专用道的通行能力为850 pcu/h/l。根据实验研究人员观测得到社会车辆的平均载客率

为1.8人/辆，公交车辆的平均载客率为26人/辆。假设最小绿灯时间为14 s，计算可得绿灯延长最大时间为13 s。

在约束条件的控制下，对控制目标函数进行试算，进行绿信比的调整。优化后交叉口信号配时如图3所示。

由延误公式计算得到信号优化前后交叉口的人总延误，如表3所示。

表3 优化前后人总延误对比表 s

从表3中数据分析得到，通过对公交信号优先控制，人总延误降低2.4%。由此说明本文提出的优化方法对公交信号优先控制有一定的效果，在一定程度上提高了乘客的出行效率。

3.3 仿真结果分析

借助调查数据进行VISSIM仿真，由车速和通行能力统计数据定义路段的交通属性，确定交通流输入情况。并结合信号相位统计情况，通过仿真数据的输出，得到信号控制优化前后的交叉口乘客总延误对比如表4所示。

表4 仿真结果对比表 s

由表4可知，优化后交叉口人总延误下降了3.4%，虽相比于模型计算的结果有一定偏差，但本文仿真结果确实验证了公交优先模型对交叉口的通行效率具有优化效果。

4 结语

本文通过研究下游停靠站和交叉口的相互作用，考虑下游停靠站排队公交车辆溢出影响，确定公交优先信号配时优化方法。以有公交专用道的单点交叉口为研究对象，分析下游停靠站对交叉口范围内交通流运行特征参数延误的影响，进而构建交叉口公交优先信号配时优化模型，使得交叉口人总延误得到优化，提高了公交车服务水平，在一定程度上减缓了交通流拥堵。