某亚音速破甲弹弹底结构破片安全性改进*
李春雷,张志彪,王雨时,严 晓,张玉峰,王秋和
(南京理工大学机械工程学院,南京 210094)
0 引言
单兵榴弹发射器所使用的小口径破甲弹由于发射初速低、射程近,在弹丸着靶起爆或在外弹道起始段意外发火爆炸时,弹底破片有回飞伤及射手的可能。若弹底破片过大,或者是整块回飞,会造成更严重后果。
为了提高毁伤特性,V.M.Gold等[1]建立了杀伤战斗部破片特性数学模型,并编制了相应的计算程序,实例验证表明该模型及其计算程序预测结果较为准确;隋树元等[2]利用数学模型优化设计了破片聚焦式战斗部的结构参数;毛亮等[3]基于遗传算法以某聚焦式破片杀伤战斗部为例,对破片杀伤威力和战斗部总质量两项指标进行了优化设计;王雨时[4]根据《引信安全性设计准则》关于延期解除保险的要求运用外弹道学、爆炸力学和威力设计理论,分析了不同形状、不同质量弹底破片在不同初速下的安全距离,即什么样的弹底破片对射手的威胁最小。
为了解决某小口径榴弹发射器破甲弹平底结构在试验中出现整块弹底破片回飞现象存在的安全性隐患问题,采用数值模拟方法对弹底结构进行改进设计,并结合发射强度的校核计算,给出满足强度要求且弹底破片较小、安全性较好的破甲弹结构参数,为小口径破甲弹结构改进设计提供参考。
1 仿真可信性说明
M406杀伤榴弹弹体结构(不含引信)如图1所示。其中图1(a)为原始结构。为了便于在ANSYS/LS-DYNA中建立模型和划分网格,并节约在AUTO DYN-3D中的计算时间,将图1(a)简化为图1(b)结构,即取消了传爆管,以部分主装药代替。
M406杀伤榴弹除引信外的各结构在数值模拟中对应的材料分别为:炸药装药为B炸药;下弹体圆柱形壳体为20号钢;下弹体球形壳体为10号钢;上弹体为2024铝合金。具体的材料模型和部分参数如表2所列。其中,上、下弹体均采用Johnson Cook强度模型和主应变失效,失效应变分别为0.5和0.6。

表1 破甲弹数值模拟各部分材料模型及部分参数[5,9]
采用显式动力学仿真软件AUTODYN-3D对破甲弹弹体爆炸破碎过程进行数值模拟,全弹包括炸药装药、上弹体和下弹体均采用Lagrange算法,划分成六面体占优网格,网格尺寸约为0.3 mm。铝合金破片的仿真结果与试验结果列入表2。
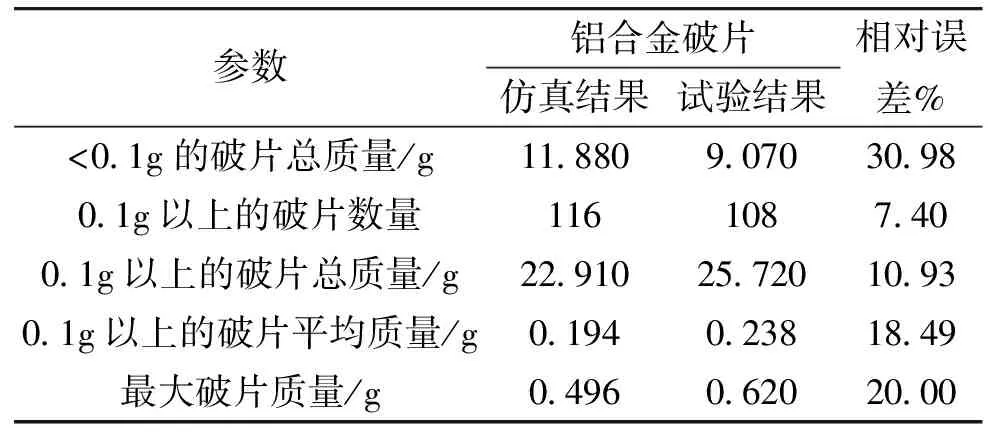
表2 铝合金破片的仿真结果与试验结果对比
表2仿真结果中破片的质量都是经过质量损失修正,仿真结果与实验结果的相对误差在可接受范围内,因此利用上述仿真方法对某破甲弹进行仿真,得到的结果是可信的。
2 数值模拟方法和初步结果
该破甲弹弹体结构(不含引信)如图2所示。其中图2(a)为原始结构。为了便于在ANSYS/LS-DYNA中建立模型和划分网格,并节约在AUTO DYN-3D中的计算时间,将图2(a)简化为图2(b)结构。图2(b)取消了传爆管(以部分主装药代替)。为便于建模,未考虑弹口螺纹结构。
2.1 数值模拟计算模型
采用上一章所述仿真方法对破甲弹弹体爆炸破碎过程进行数值模拟。
考虑到数值模拟的主要关注点在弹体底部的破碎情况,因而为了提高计算效率,全弹包括炸药装药、药型罩、上弹体和下弹体均采用Lagrange算法,并划分成六面体占优网格,网格尺寸约为0.5 mm。
2.2 数值模拟材料模型
破甲弹除引信外的各结构在数值模拟中对应的材料分别为:炸药装药为JH-2;药型罩为Cu-OFHC;下弹体为2024铝合金;上弹体为高强度钢。具体的材料模型和部分参数如表3所列。其中,药型罩和上、下弹体均采用Johnson Cook强度模型。上、下弹体均采用主应变失效,失效应变分别为0.6和0.5。

表3 破甲弹数值模拟各部分材料模型及部分参数[5,7-8]
2.3 数值模拟初步结果
数值模拟采用点起爆方式,起爆点设置如图2(b)所示。在计算机上对该破甲弹原始结构[图2(b)]的动态破碎过程进行计算。图3所示为数值模拟得到的原始弹体68 μs时的破碎图像,可看出弹底存在整块的大型破片(碟状)向后回飞,该破片重约9.947 g。该爆炸现象与试验能观察到的弹底破碎结果(破片大小)较为一致。
因此,采用上述软件、计算模型和材料模型能够较为准确的模拟该小口径破甲弹的爆炸破碎情况。
3 结构改进设计与数值模拟
为了防止弹底产生较大破片,拟改进弹底结构。现改进设计三种下弹体和相应的装药结构(上弹体与药型罩结构不变),并数值模拟其爆炸过程。
3.1 3 mm等壁厚球形弹底
图4所示为3 mm等壁厚球形弹底结构,弹底隔板形状由平面改为球面,厚度为3 mm。从理论上讲,球面对应的弧度越大,破碎性就越好,但装药工艺就越复杂。考虑两者之间的平衡,现将弧面对应的圆心角取为88°。弹底以上结构不变。
由AUTODYN-3D软件对其爆炸过程进行数值模拟后,得到如图5所示的3 mm等壁厚球形弹底破碎图像。弹底破碎为很多小破片,其中最大破片质量0.17 g。该弹底结构能避免产生大块弹底破片。
3.2 4.4 mm等壁厚球形弹底
数值模拟结果显示,弹底部分已较为均匀的破碎,最大破片质量0.63 g。
3.3 十字刻槽型弹底
图6为十字刻槽型弹底结构,由原弹底结构从外侧向内加刻十字槽而成。最小厚度4.4 mm(槽深1.1 mm),最大厚度5.5 mm,装药量不变。
如图7所示,数值模拟发现虽然加设了十字形刻槽,但仍会发生整块弹底破片回飞现象,最大破片质量7.30 g。因而十字刻槽型弹底结构方案无法满足减小弹底破片质量的目标。
4 各弹底结构发射强度校核
该小口径破甲弹由榴弹发射器发射,火药气体直接推动弹丸向前飞行,最大膛压为98 MPa。
根据弹底发射强度相关理论[6]计算可得原始结构5.5 mm厚铝合金制平底发射强度在98 MPa的最大膛压下满足要求。
由于弹底壁厚较薄,其壁厚比曲率半径小得多,故其应力可按薄壁容器公式计算。根据球形弹底发射强度相关理论[6]计算可知3 mm与4.4 mm等壁厚球形弹底发射强度在98 MPa的最大膛压下均能满足要求。由于理论计算将火药气体最大压力时间假设为无穷大,所以所得结论会偏于保守。
由于十字槽弹底结构复杂,借用简单结构的理论公式只是近似估算,故采用有限元数值模拟方法校核弹底强度。
弹底的等效载荷情况如图8所示。现估计弹底所受98 MPa的火药气体压力持续时间为1 ms。P为火药气体压力,Pi为装填物后坐压力。根据弹底发射强度相关理论[6]可计算出Pi的大小为33 MPa。
采用ANSYS Workbench 14.0对下弹体的应力情况进行数值模拟。约束下弹体上端面,如图9所示对下弹体加载压力,然后根据弹底强度校核相关理论[6]计算所得的惯性力(对下弹体加载一个与装填物压力方向相同,大小为481 210 m/s2的加速度)。将模型划分成四面体网格,网格尺寸为1 mm,其中下弹体材料为2024铝合金。
如图9所示,十字槽弹底所受最大应力处于十字槽中心部分,其值为574.88 MPa,该值大于2024铝合金的许用应力,因而该弹底结构发射强度在98 MPa的最大膛压下不满足要求。
5 结论
通过结构强度校核结果可知,原始设计的5.5 mm厚铝合金制平底结构发射强度在98 MPa的最大膛压下满足要求。但通过爆炸过程数值模拟结果可知该弹底结构弹底破片过大,无法满足减小弹底破片质量的要求。
十字刻槽型弹底结构强度校核结果为发射强度在98 MPa的最大膛压下不满足要求。同时,由爆炸过程数值模拟结果可知,最大弹底破片质量7.30 g,无法满足减小弹底破片质量的要求。
3 mm与4.4 mm等壁厚球形弹底的发射强度在98 MPa的最大膛压下满足要求,并且由爆炸过程数值模拟结果可知3 mm和4.4 mm等壁厚球形弹底产生的破片较小,质量分别为0.17 g和0.63 g。因此3 mm等壁厚球形弹底为比较合适的弹底结构,产生的破片较小,对发射人员的威胁较小。

