SVM与PSOHF参数优化装备机械传动齿轮故障诊断*

仝 蕊，康建设

（陆军工程大学石家庄校区，石家庄 050003）

0 引言

齿轮以其传动比准确、稳定可靠、寿命长等优点广泛应用于航空、船舶、运输机械、电力系统等各类设备中，但由于长期连续工作在高载荷、高转速环境下，极容易受到损害和出现故障。作为装备机械传动系统的核心，齿轮的损伤或失效会导致整个传动系统的故障，从而引起重大安全事故[1-2]。因此，齿轮的故障识别与诊断研究具有十分重要的学术和工程应用价值。

齿轮故障诊断常要求具备大量训练样本数据或先验知识，但在许多大型机械设备中，很难获取大量典型故障数据[3]。支持向量机（SVM）是一种新型学习机器，它较好地解决小样本、非线性等实际问题，并克服其他方法如人工神经网络等方法中收敛速度慢、训练时需要大量数据样本等不足[4]，极大提高了学习方法的泛化性能。SVM分类结果在很大程度上取决于模型参数。其中核函数的类型及相关参数对分类结果影响很大，所以SVM分类要考虑寻求一种快速且有效选择最优模型参数的方法[5]。

本文首先针对粒子群算法在迭代后期容易陷入局部最优的问题，选用蜜蜂觅食机制改进粒子群算法（PSOHF）[6]。然后提出了一种基于 PSOHF 的SVM参数优化方法，采用PSOHF对支持向量机模型参数进行优化，从而提高支持向量机的分类性能。最后，利用小波包分解提取故障特征向量，并进行了分类实验应用于实际齿轮故障诊断中，实验结果验证了所提方法的可行性和有效性。

1 SVM分类原理

SVM是建立在统计学习理论基础上的一种机器学习方法[7]。给定训练样本为（xi，yi），xi∈Rn，yi∈{-1，1}是类别标签，利用SVM构造一个目标函数，寻求最优分割超平面：

其中w表示超平面法向量，b表示偏移量。若线性不可分，需求解以下最优方程：

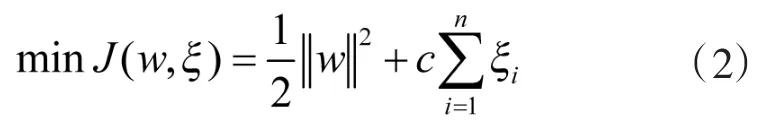
约束条件为

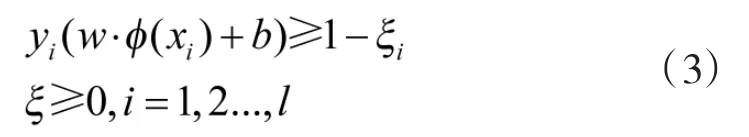
具体步骤为：通过目标函数将训练数据中的点映射到高维空间中，通过寻找最优的线性超平面，使训练样本在此高维空间中拥有最大分类间隔。式（4）是得到的超平面判定函数

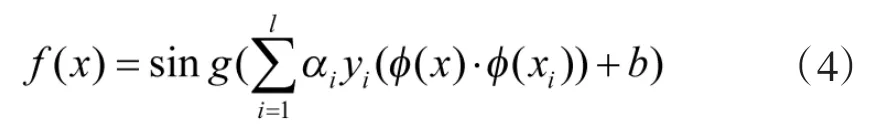
其中αi（i=1，2，…，s，s≤1）为Lagrange因子。通过寻找满足 Mercer条件的核函数 K（xi，x）进而替代式（4）中的点积（φ（x），φ（xi）），可以得到下述SVM的判决函数：

αi（i=1，2，…，s，s≤1）是少数训练样本对应的非零因子。

支持向量机的核心思想是引入核函数，不同的核函数会导致的推广性能有所不同，因此，如何根据具体问题选择恰当的核函数是应用领域遇到的一个重大难题。核函数参数如惩罚因子C和核参数g，对SVM的分类算法有着重要影响，因此，有必要选择合适的智能算法对这些参数进行优化调整。

2 蜜蜂觅食算法（PSOHF）原理

蜜蜂觅食算法作为一种新兴的群智能算法，模拟自然界中蜜蜂群体觅食方式，具有较强的全局搜索能力[8]。首先设定粒子群算法的空间维度为D，粒子数为n。将第i个粒子的当前位置记为Xi=（xi1，xi2，...，xiD），其历史最优位置为 Pi=（Pi1，Pi2，...，PiD），粒子的速度为 Vi=（vi1，vi2，...viD），则粒子的位置更新采用如下公式：

式中，c1和c2是加速因子，一般为非负常数；r1和r2为均匀分布在[0，1]之间的随机数；ω为惯性权重系数。

蜜蜂觅食算法的生物学基础是蜜蜂在采蜜觅食过程中的智能表现[9]：1）侦察蜂在蜂巢附近搜索蜜源；2）找到蜜源后记录相关信息，并将侦察蜂换为雇佣蜂；3）根据信息选择蜜源。采用模拟蜜蜂这种搜寻方式并将其融入粒子群算法，提高算法的性能。

蜜蜂觅食优化粒子群算法（PSOHF）基本原理：首先粒子群初始化，群内每个粒子先以PSO的更新公式进行搜索，当粒子i的个体最优位置在连续的k次迭代中没有明显改善时，执行邻域搜索算子提高算法在搜索范围内的开发能力，以便跳出局部最优。设执行邻域算子条件为fpit-fpit-k=0，fpit表示pit的适应度值，pit=[pi1t，pi2t，，piDt]表示粒子 i的第 t次迭代时的最优个体位置。邻域算子的执行方式上，设置O邻域算子（Origin Neighbor Search）和R邻域算子（Rrigin Neighbor Search）。在局部最优位置的一定邻域范围内进行随机初始化，进一步搜索最优值。

PSOHF算法步骤如下：

1）非对称地初始化粒子群的速度和位置。

2）计算粒子的适应度，将每个粒子置于其历史最优位置，进而得到初始的全局最优位置。

3）利用式（6）、式（7）更新粒子的速度和位置。

4）对更新后的粒子的适应度，进行计算并与其历史最优值相比较，以更新个体最优位置。

5）判断是否执行邻域算子，是则进入步骤6），否则转入步骤10）。

6）选择最优的个体位置。

7）执行邻域算子。

8）在最优个体邻域内寻优。

9）选择总体最优位置。

10）迭代次数加1。

11）判断是否达到最大迭代次数，是则转入步骤 3），否则进入步骤 12）。

12）结束，输出结果。

3 基于PSOHF算法的SVM参数优化

3.1 参数优化过程

支持向量机性能的优化，其实质是利用计算机寻踪算法对支持向量机的分类参数进行优化选择。通过人工确定参数，采用交叉验证的方式也能进行一定程度上的寻优，但是这样的方式不仅费时费力且不能保证参数最优。利用智能算法对支持向量机参数寻踪，具有良好的全局和局部搜索能力，可以合理优化分类器参数，获取最优参数。利用蜜蜂觅食机制改进的粒子群算法优化SVM模型参数[10]，主要是优化惩罚参数c和核参数g。其基本流程图如图1所示：

图1 优化SVM参数流程图

增加了基于蜜蜂觅食特征改进粒子群算法的执行邻域算子操作，步骤如下：

步骤1 设置SVM初始参数，包含最大迭代次数、微粒初始速度vi0、微粒最大允许速度vdmax、随机生成初始微粒xi0、群体规模等。微粒向量的元素分别对应的是惩罚参数c和核参数g。

步骤2 计算每个微粒适应值。以预测样本的实际值与预报值误差最小为目标函数，如下：

步骤5 基于蜜蜂觅食特征的微粒移动操作。判断是否满足执行邻域搜索算子条件，即粒子i的个体最优位置在连续的k次迭代中没有明显改善时，执行邻域搜索算子提高算法在搜索范围内的开发能力，以便跳出局部最优。若是，则认为陷入了局部最优，执行PSOHF算法步骤6）；若否，则执行PSOHF算法步骤10），从而跳出局部最优。

步骤6 判断迭代次数是否已经达到最大迭代次数，是则计算结束；否则返回步骤2。

3.2 数据验证

为了验证PSOHF优化SVM的效果，选用UCI数据库中Wine数据库进行核函数优劣测试。其中包含有3种不同类型的葡萄酒化学成分分析数据，共含178个样本，每个样品含13个特征分量。对各类样本进行分组，前50%作为训练样本，后50%作为测试样本。对同一训练集和测试集选用普通交叉验证法、PSO算法、PSOHF算法对比分析结果。设置PSO算法和PSOHF算法参数：加速度因子c1=1.5，c2=1.7，最大进化数100，种群最大数20。交叉验证时，惩罚参数c的取值范围为[-4，4]，核参数g的取值范围为[-4，4]。支持向量机核函数选用径向基核函数，多分类策略为一对一算法，结果如表1所示：

表1 支持向量机性能优化对比结果

算法优化支持向量机参数的过程中，最重要的部分是算法适应值的选取，适应值选择训练集当前参数配置下的随机剖分后交互验证获得的平均准确率，平均准确率最高时，得到寻优过程的最佳适应值，对应输出最优参数。

图2 PSO优化SVM适应度曲线图

图3 PSOHF优化SVM适应度曲线图

由表1可知，采用普通交叉验证法对SVM进行寻优得到的最佳参数为2.297 4和4，准确率为90%，运行时间为6.5s。PSO与PSOHF采用同样的参数设置，分别对训练样本进行训练，适应度函数演化曲线如图2、图3所示。PSO训练样本准确率在第59代时达到最优值并保持稳定，相对于PSOHF算法，收敛速度慢，精度也略低，此时惩罚因子c=4.826 8，核函数参数g=3.012 8。同时对比参数搜索轨迹，PSO中搜索始终在[-1 1；-1 1]的坐标范围内，而PSOHF算法中蜜蜂个体的觅食范围则要远大于此。由此PSO对小坐标区域搜索精度高，不利于搜索到全局最优解；PSOHF算法则通过平衡搜索精度的方式在一定程度上扩大了群体搜索范围，有利于取得更优的效果。用PSOHF对SVM进行参数寻踪的试验表明，最佳参数为5.204 8和3.097 1，运行时间明显缩短，因此，PSOHF算法更适合于SVM的性能优化。

4 齿轮裂纹故障诊断实验

4.1 采集实验数据

为验证本文所提方法的有效性与实用性，将该方法应用于齿轮裂纹故障诊断实验中。通过实验室机械振动及故障模拟平台进行实验。实验负载为10 Nm，转速为 800 rpm，采样频率为 20 000 Hz，采样时间为6 s，利用数据采集板及Labview软件将采集到的振动信号存入电脑。传感器位置表示为CH1、CH2、CH3、CH4。实验台布置及传感器位置如图4所示。

图4 变速箱预植故障实验台及传感器位置

将齿轮齿根裂纹故障加工在输出轴（低速轴）大齿轮齿根上，进行齿轮齿根裂纹预植故障实验。图5所示为齿根裂纹加工位置及宽度示意图。齿根裂纹采用线切割以α角度进行加工，深度分别为1 mm、2 mm和5 mm。本文分别选用（正常、裂纹深度1 mm、2 mm和5 mm）4种退化状态分别进行实验，并采集各状态下4个通道6 s的振动数据。

图5 齿根裂纹位置

该变速箱低速轴齿轮（故障齿轮）齿数为Z1=81，中间轴大齿轮齿数Z2=64，中间轴小齿轮齿数Z3=19，高速轴齿轮齿数为Z4=35。输入轴（轴3）转速V3为800 rpm，轴3输入转频为：f3=800/60=13.33 Hz。设输出轴（轴 2）转频为：f2，传动比 i=Z4/Z2=f2/f1，则f2=7.29 Hz。一级啮合频率：fm1=f1×Z4=f2×Z2=466.6 Hz。轴2转速V2=f2×60=437 rpm；轴1转频为f1，传动比i=Z3/Z1=f1/f2，则可得故障齿轮转频f1=1.71 Hz；二级啮合频率：fm2=f2×Z3=f1×Z1=138.5 Hz。图6给出一组各状态下的齿轮振动信号时域图。

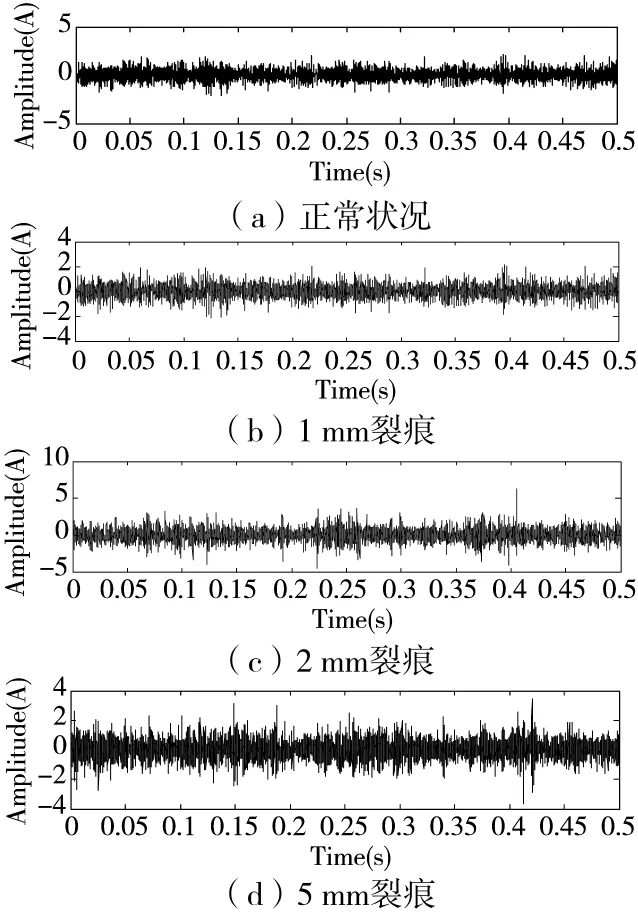
图6 齿轮振动信号时域图

4.2 小波包能量特征提取

根据实验数据可知，故障齿轮的特征频率f1=1.71 Hz极小易淹没在强噪声背景下。如果选择故障特征频率的振幅作为特征向量，进行特征的自动提取较为困难。因此，本文利用小波包变换将振动信号分解，采用基于小波包能量的特征提取算法，对齿轮故障信号进行分析与特征提取[11]。

小波包分解将原始信号分解为近似信号（低频信号）和细节信号（高频信号）。在接下来的每一层分解中，将低频信号和高频信号进一步分解为更高层的近似信号和细节信号。小波包是从原始信号分级向下分解，其中每个节点都有对应的小波包系数，而这个系数决定了频率的大小。其分解的过程如图7所示。

图7 小波包分解图

当齿轮表面产生裂纹时，运转中产生的冲击会激起整个系统的高频固有振动，从而导致不同频带的能量分布发生变换，可利用小波包分解实现振动信号频带的自动划分，从而进行能量特征提取。以各频带信号的相对小波能量值[12-14]作为齿轮故障信号的特征向量，其计算过程如下：

首先，利用小波包变换对原始信号f（t）进行J=3层分解，选择db8小波基函数，可得到A-H的8段不同的低高频带相邻组合的信号，如图7所示。其次，获取小波包分解的第3层各节点的重构信号。记EJ为第J层各节点重构信号的能量，即第i个节点的范数平方（平方和），AJ为低频近似分量系数，DJ为高频系数，总的能量表达式为：

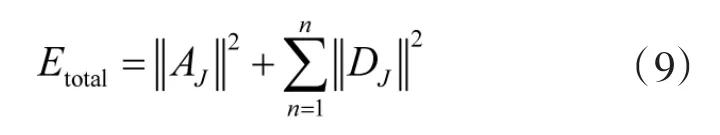
简化公式，将 AJ表示为 DJ+1，式（9）表示为

最后，将各频带信号的能量值表征为相对小波能量ρj，其表达式为：

由式（11）求得各段频带信号的能量值即相对小波能量ρj作为提取的信号特征[13]，用于SVM的训练分类。因篇幅有限，列举部分齿轮正常、裂痕1 mm、裂痕2 mm和裂痕5 mm这4种状态下，每段齿轮振动信号在A-H频段上的相对小波能量值，如表2所示。

表2 4种状态下相对小波能量

4.3 实验结果与分析

本节对算法进行验证。选取4种状态下的齿轮振动信号样本共80组作为训练参数集，设置正常为1，1 mm裂纹为2，2 mm裂纹为3，5 mm裂纹为4。经过多次试验后，确定粒子群寻踪参数为：加速度因子c1=2.0，c2=1.5，最大进化数200，种群最大数20，适应度选用训练集随机剖分后交互验证的准确率平均值。利用本文提出的PSOHF算法对SVM的参数进行优化选择和分类处理。适应度选用训练集随机剖分后交互验证的准确率平均值。支持向量机核函数选用径向基函数，多分类策略选用一对一算法，利用训练集进行支持向量机参数寻优后适应度曲线如图8所示：

图8 故障分类模型优化适应度曲线

从图8的寻优结果得出，当训练集采用4类故障数据共同组成时，PSO寻优最佳适应度为98%，相对应的最优分类参数为5.177 1和3.125 1，将最优参数和训练集输入支持向量机，获得相应的4故障分类模型。为了验证齿轮变速箱多分类模型的准确性，取4种状态下的特征数据各20组组成4个测试数据集，分别用多故障分类模型进行分类测试，测试结果如表3、图9所示：

表3 故障分类模型测试结果

图9 优化参数后测试样本分类诊断结果

4种状态测试数据的分类结果表明，用PSOHF-SVM建立的齿轮分类模型可以较准确地识别正常状态和几种裂痕状态的数据，在2 mm裂痕时出现了一定的误差，考虑实验数据本身存在一定的随机误差，无法像仿真数据般贴合分类器，且分类准确率都达到了95%以上，错误识别很少。因此，PSOHF-SVM模型适用于齿轮故障状态分类诊断。

5 结论

针对基本粒子群算法优化算法在迭代后期容易陷入局部最优的问题，利用蜜蜂觅食特性对粒子群算法进行了改进。蜜蜂觅食改进粒子群算法在一定程度上克服了早熟收敛的问题，具备更好的全局寻优能力。在此基础上，针对支持向量机的模型参数选择对其分类性能影响巨大的问题，提出了一种基于PSOHF的SVM参数优化方法，并将该方法应用于装备机械传动齿轮故障诊断。与SVM和粒子群算法优化SVM的分类结果相比，蜜蜂觅食改进粒子群算法优化SVM具有更高的分类正确率，具有较好的工程应用价值。