支腿-轮胎载荷分配比对混合支撑发射过程的影响*

王玲丽，马大为，张震东，朱忠领，王泽林

（南京理工大学机械工程学院，南京 210094）

0 引言

导弹无依托随机发射是一种新型作战模式，在作战过程中，导弹发射将不需要依托预设阵地，随机选取发射场地，即时进行战斗[1]，这种导弹无依托发射方式相较于传统发射方式在很大程度上节省了发射准备时间，提高了作战效率。

现有的导弹发射装置的支撑方式包括刚性支撑，混合支撑，柔性支撑。刚性支撑是指导弹起竖与发射过程中载荷完全通过千斤顶传递到地面；混合支撑是支腿与轮胎同时承受载荷；而弹性支撑指载荷仅通过轮胎传递到地面。郑夏[2]研究了发射箱箱口回弹的变化规律，提出将箱口回弹情况纳入出箱安全性分析因素的方法。闫攀运[3]建立了车载系统快速仿真模型，研究了发射管底座-支腿载荷分配比和附加因子对发射稳定性的影响。高星斗[4]研究两种不同发射角下车载导弹倾斜发射对导弹发射箱体振动的影响。陈大雄[5]验证了车载导弹发射时柔性支撑的可行性。

目前，尚未有人针对混合支撑支腿、轮胎载荷分配比对导弹发射稳定性有何影响做出研究。本文基于显式动力学方法，运用有限元分析软件ABAQUS对导弹系统发射过程进行建模仿真运算，针对某型导弹在混合支撑这种支撑方式下，研究不同支腿、轮胎载荷分配比对导弹发射过程中稳定性的影响。

1 显式非线性动力学

1.1 动力学问题基本方程

非线性动力学求解的基本方程形式如下[6]：

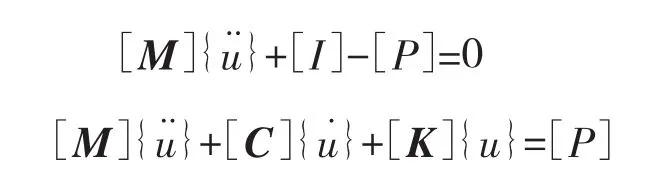
其中：[M]为质量矩阵；[C]为阻尼矩阵；[K]为刚度矩阵；为粘性效应项，考虑阻尼、粘塑、粘弹等效应；[P]为外部激励作用；为节点加速度向量；为节点速度向量；为节点位移向量。

1.2 显式时间积分

1）节点计算

①动力学平衡方程

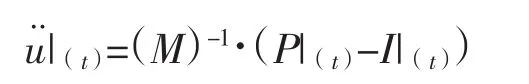
②对时间显式积分

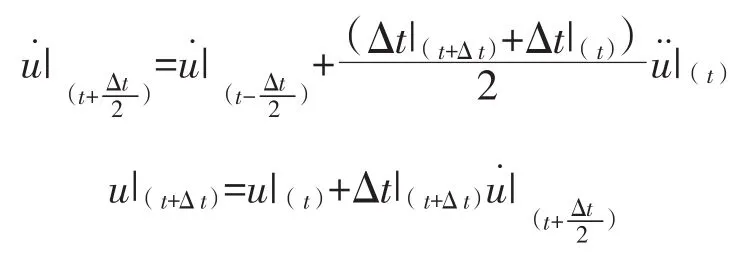
2）单元计算

②根据本构关系计算应力σ：

3）设置时间t为 t+△t，返回到步骤1）

显式方法最显著的特点是没有整体切线刚度矩阵，而且由于是显式地前推模型的状态，所以不需要迭代和收敛准则。

1.3 显式方法的条件稳定性

稳定性限制以系统中最高频率（ωmax）来定义。无阻尼的稳定性限制由下式定义：

有阻尼的稳定性限制由下式定义：

式中，ξ为最高频率模态的临界阻尼。

2 导弹发射系统仿真模型

2.1 系统简化

车载导弹武器系统主要包括发射车、起竖装置、发射装置、导弹等组成部分。导弹在发射过程中力学环境非常复杂，本文在计算时只考虑发射装置对发射过程的影响。图1为某双联装导弹发射系统简化示意图。

图1 车载导弹系统混合支撑简化模型

如图1所示，整个车载导弹系统简化为车头、车架、发射箱、导弹、支腿、轮胎、起竖油缸、适配器等部件；该模型中将弹体简化为刚体，车头简化为质量点，耦合于车架上，其余部件均设置为可变形体，为了简化建模，将系统中的起竖液压油缸、支腿、轮胎、悬架等用弹簧阻尼代替，车桥、车轮轴等用梁单元简化，由于混合支撑方式中，支腿的变形量远小于轮胎的变形量，所以设定支腿处的连接单元属性为刚性连接。

整个发射系统可以看作关于面对称的结构[7-9]，规定与发射车前进方向为Y轴正向，Z轴的正方向沿着重力垂直向上，X轴根据右手定则确定。

2.2 轮胎、支腿载荷分配

混合支撑采用的支腿与轮胎共同支撑，整个导弹发射系统（不含地面）质量约为2.35×104kg，以支腿、轮胎各承受一半的载荷为例，即发射系统8个轮胎共承受1.175×105N，由于整个发射系统质心不是处于模型的几何中心。经过测量，整个导弹系统的质心所在位置如图2所示。其中，F1、F2、F3、F4分别表示沿Y轴方向从左往右四组车轮中每组车轮所承受的载荷。

图2 轮胎承受一半重量时轮胎受力图

将其简化为平面力，根据平面力系平衡方程

为了简化计算，将导弹发射车前两组轮胎所受载荷等效为大小相同的载荷，即F1=F2，同理，后两组轮胎所受载荷F3=F4，由此计算出

2.3 载荷分配工况

设支腿所承受的总载荷为Q1，发射系统总重为Q2，定义支腿承载占总重的比例为R，其中，

R值选取3个代表性的数值进行分别进行计算，选定R值为1/4，1/2，3/4分别进行计算，由于导弹发射系统动力学分析计算动态响应之前需要进行静平衡分析得到系统的平衡位置，将计算出的初始受力状态导入导弹发射系统的动态模型。

3 仿真结果与分析

计算结果显示导弹完全出筒时间约为0.822 s。本文主要从发射车稳定性以及导弹出筒品质这两方面考虑支腿、轮胎载荷分比配对导弹发射过程的影响。

3.1 支腿、轮胎载荷分配对发射车稳定性影响

以导弹前进方向的视角为正方向，发射系统分为左右两侧，选取左侧轮胎动态响应进行分析。图3、图4分别为导弹左前轮与左后轮在导弹发射过程中轮胎载荷随时间变化曲线。

由图3、图4可看出，R值越小，轮胎在法向上的位移越大，R值不同，但前后轮胎在法向上的位移量随时间的变化规律基本一致。左后轮R值为1/4与R值为3/4时，其同一时刻位移量相差约为6.54 mm，而左前轮R值为1/4与R值为3/4时，其同一时刻位移量相差约为3.62 mm。同时，对比图3、图4可发现，由于后轮所承受的载荷比前轮大，发射车后轮位移量随R值变化的影响比前轮大。

图3 左后轮位移曲线

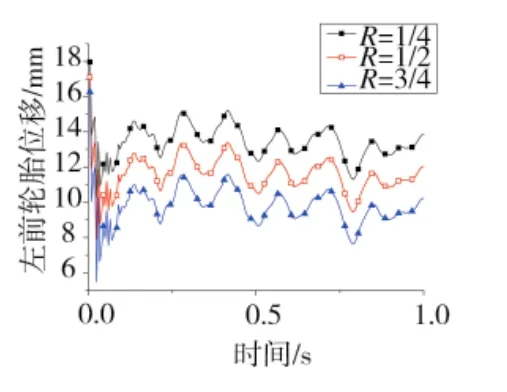
图4 左前轮位移曲线

图5为左前轮与左后轮在3种工况下轮胎所受载荷随时间变化曲线，从图中可以看出，R值分别为1/4，1/2，3/4时，左前轮与左后同一时刻所受法向轮载荷相差约为5.3 kN，3.6 kN，1.9 kN。轮胎所分配载荷越大，前后轮法向载荷差值越大，后轮相较于前轮负担更重，这与载荷分配比的大小与轮胎在法向位移上的影响是一致的。

图5 轮胎载荷随时间变化曲线

图6 驾驶室垂向位移曲线

图7 驾驶室垂向速度曲线

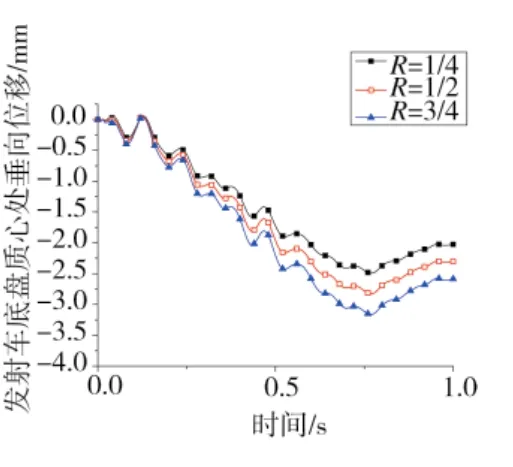
图8 发射车底盘垂向位移曲线

图9 发射车底盘垂向速度曲线

图10 发射筒筒口横向位移曲线

图6、图7为导弹系统中驾驶室的垂向位移曲线与垂向速度曲线，图8、图9为发射车底盘质心处的垂向位移曲线与垂向速度曲线。通过驾驶室以及发射车底盘处的位移与速度随R值的变化的对比图可发现，R值为3/4时，驾驶室与底盘质心在垂向上的波动最大。

3.2 支腿、轮胎载荷分配比对导弹出筒的影响

图10、图11分别为发射筒筒口横向位移、纵向位移随时间变化曲线，导弹发射初始时，筒口横向位移与垂向位移均时间增大，0.3s处，垂向与纵向位移均达到最大，之后位移呈减小趋势。表1为不同支腿、轮胎载荷分配比下发射筒横向、垂向位移在0.3 s的位移量。由表1可知，R为1/2相较于R为1/4的横向位移峰值增大了25.13%，垂向位移峰值增大了11.17%，R为3/4相较于R为1/4横向位移峰值增大了50.13%，垂向位移峰值增大了33.47%。

表1 发射筒位移峰值

图11 发射筒筒口垂向位移曲线

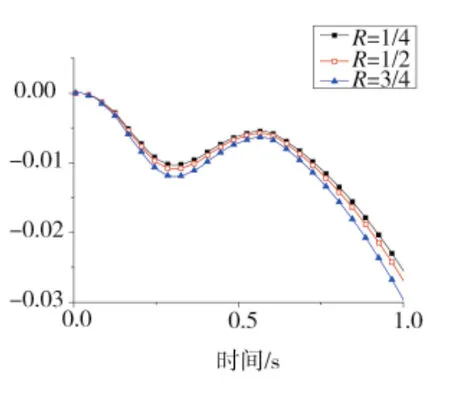
图12 导弹质心俯仰角度曲线

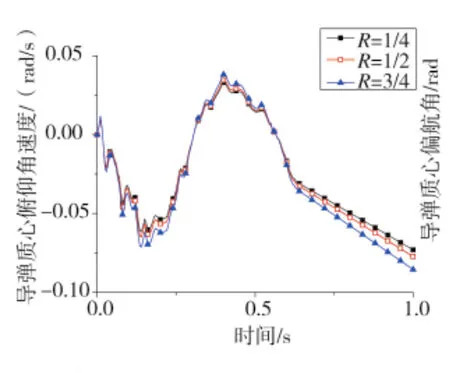
图13 导弹质心俯仰角速度曲线

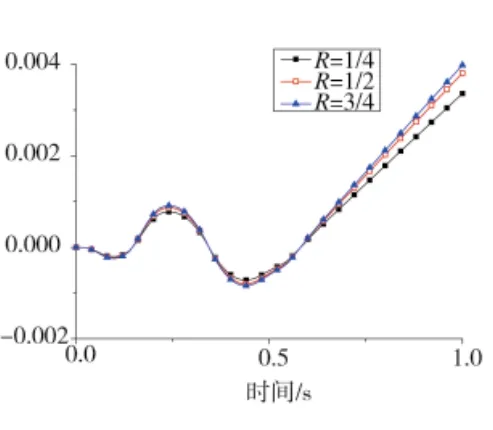
图14 导弹质心偏航角度曲线

图15 导弹质心偏航角速度曲线

图12、图13分别为导弹质心处的俯仰角度与俯仰角速度曲线，图14、图15分别为导弹质心处偏航角度与偏航角速度曲线。从这4幅图可看出导弹质心处的俯仰角度与俯仰角速度以及偏航角度与偏航角速度在一定程度上均随着R值的增大而增大。3种工况中，R为1/4时导弹俯仰角度与俯仰角速度以及偏航角度与偏航角速度均最小。

4 结论

本文通过在通用有限元软件中建立的多体动力学模型，针对3种不同的支腿、轮胎载荷分配比进行分析，可以得出如下结论：

1）支腿、轮胎载荷分配比不同，在导弹发射过程中对轮胎在法向上的位移量有一定的影响，混合支撑时，轮胎所承受的载荷越大，轮胎在法向上的位移越大。

2）支腿、轮胎载荷分配比不同，在发射过程中对发射车的稳定性以及导弹出筒姿态也有一定的影响，综合考虑驾驶室与发射车底盘质心处的纵向位移与速度，可以得出，对比这3种工况，R为1/4时，发射车在纵向上的跳动最小，在此种工况下发射车较为稳定。同时发射筒筒口的横向位移与垂向位移较小，导弹的俯仰角速度与偏航角速度较小，导弹出筒姿态较好。

3）通过计算并分析3种工况下的导弹发射过程的动态响应，对比其导弹发射过程扰动的大小，为导弹发射装置混合支撑时载荷分配的选择提供了参考。