基于分阶式力引导的自动装配定位方法

武维维，邵晓东，刘焕玲

(西安电子科技大学 电子装备结构设计教育部重点实验室，陕西 西安 710071)

0 引言

虚拟装配技术是现代先进制造技术领域的重要研究课题。利用虚拟装配技术仿真产品装配过程有利于在产品的早期设计阶段发现后续生产中的装配工艺问题，为产品设计的改进提供参考。据统计，产品的装配费用占生产成本30%～50%以上[1]，应用虚拟装配技术提高产品装配效率和质量对于降低生产成本、增强企业的市场竞争力具有重要意义。

在现实的装配作业中，装配者通过视觉感知零件的位置和姿态信息，通过触觉感知零件的物理属性信息(重量、转动惯量、重心等)及零件间的物理约束信息(接触力、摩擦力等)，并根据这些信息施加适当的装配力和装配力矩，对零件进行准确引导与定位。然而，在虚拟装配环境中，受制于虚拟现实技术的发展，大部分虚拟装配系统既难以构建全面真实的空间深度感，以使装配者感知到零件的精确位姿信息[2]，也难以提供准确实时的触觉反馈，以使装配者感受到零件间的相互作用信息[3]。同时，由于虚拟交互设备精度不高，导致装配力和装配力矩输入不准确[4]，零件装配定位困难且装配过程缺乏真实感。因此如何从人的装配意图出发计算实时的装配力与装配力矩，对零件进行准确引导定位，是目前虚拟装配领域重要的技术问题。

近年来，国内外学者对虚拟装配引导定位技术进行了大量研究。Tching等[5]分析了触觉交互设备装配引导误差大，后期装配定位困难的问题，提出动态运动学约束辅助装配引导的方法，提高了装配定位的效率和精确度；Dewar等[6]通过碰撞捕捉或近似捕捉的方法识别虚拟环境中的几何约束，并根据该约束直接将装配件调整到目标位姿，以实现装配定位；Yang等[7]研究了装配约束的统一表示方法，以及约束和自由度的相互映射方法，提出基于广义坐标系的装配引导算法；Liu等[9]开发了一套用于约束捕获、定位求解和受约束运动的约束行为管理器，提高了装配约束识别效率，降低了利用虚拟引导设备进行装配定位的难度；彭高亮等[10]将模糊评判算法应用于装配零部件间几何约束的自动识别，提高了装配特征匹配的效率和准确度；张丹等[11]利用包围盒作为代理特征，代替实际约束元素进行装配约束识别，并通过位姿变化元素分解方法简化了装配件在约束下的定位求解；刘振宇等[12]提出一种基于装配语义的装配引导方法，将识别出的装配语义映射为装配约束，通过零部件间自由度的求解实现约束导航与准确定位。

然而，上述方法均无法真实模拟产品实际装配过程。这些方法大多通过几何约束限制装配件的自由度来使其沿预定轨迹运动，一旦装配件满足预定义约束匹配条件，就将其直接定位至目标装配位姿。但真实的装配环境并不存在这些几何约束，也不可能根据匹配的装配特征直接跳变到目标位姿。在实际装配过程中，零件的装配定位是通过装配者施加的装配力和装配力矩，以及零件间的相互接触碰撞的共同作用完成的。此外，装配操作的实施主体是人，装配过程人机条件(如装配区域的可视性、装配操作的舒适程度、装配者的疲劳程度等)的优劣对产品可装配性具有至关重要的影响,只有将人机因素融入进产品装配过程，才能实现可靠的装配过程仿真，进而评估产品的真实装配性能。

装配件的引导定位实质是通过施加装配力和装配力矩驱动装配件进行移动和转动，以消除装配件的装配特征(简称装配特征)与目标件的装配特征(简称目标特征)的位置和姿态误差。为了在不依赖虚拟交互设备的条件下模拟人的装配操作，并使仿真出的虚拟装配过程符合现实装配过程的特点，本文提出一种基于分阶式力引导的自动装配定位方法。首先根据已积累的装配经验以及装配过程各阶段施加的装配力和装配力矩的不同特点，将装配过程分为装配空间漫游阶段、找孔阶段、半入孔阶段、入孔阶段。然后从人对物体位姿的实际认知出发，提出一种面向装配过程仿真的物体位姿描述方法及控制策略。利用蒙特卡洛方法模拟人机因素对装配力和装配力矩的影响，以便将人机因素融入产品装配仿真过程中来分析人机条件的优劣对产品可装配性的影响。在此基础上，根据装配者在装配过程各阶段的装配意图，分别构建各阶段的装配力与装配力矩的计算模型，以体现实际装配操作中所具有的智能性。最后在虚拟环境下建立装配件的动力学运动方程组，利用动力学仿真完成产品的精确装配定位。

1 装配仿真过程各阶段描述

首先，根据装配任务要求交互输入装配件初始位姿参数，由装配空间漫游阶段开始进行自动装配仿真。根据装配件与目标件当前的位姿偏差估计值计算装配力与装配力矩，驱动装配件向目标位置靠近，并对装配件姿态进行初步调整。由于装配者对装配件与目标件的位姿偏差信息的判断存在一定误差，手工装配操作也存在一些固有的模糊性和随机性，很多情况下装配者并不能准确直接地将装配件放置到孔口处，在装配件与目标件发生接触后，有时会进入一个找孔阶段。装配件以适当的接触力贴紧目标件表面，并克服摩擦力向目标位置滑动，同时施加装配力矩，使装配件在移动过程保持姿态平衡。在接近目标位置时，装配件失稳，进入半入孔阶段。以线性弹簧力学模型模拟装配力，以扭转弹簧力学模型模拟装配力矩，对装配件进行扭转和轻微移动，经过若干次位姿调整试探，在位姿误差达到允许范围内时，装配件底面会完全进入孔口所在平面之下，装配件进入入孔阶段。最后在重力的作用下向目标位置移动，完成装配件的精确定位。装配仿真过程各阶段如图1所示。

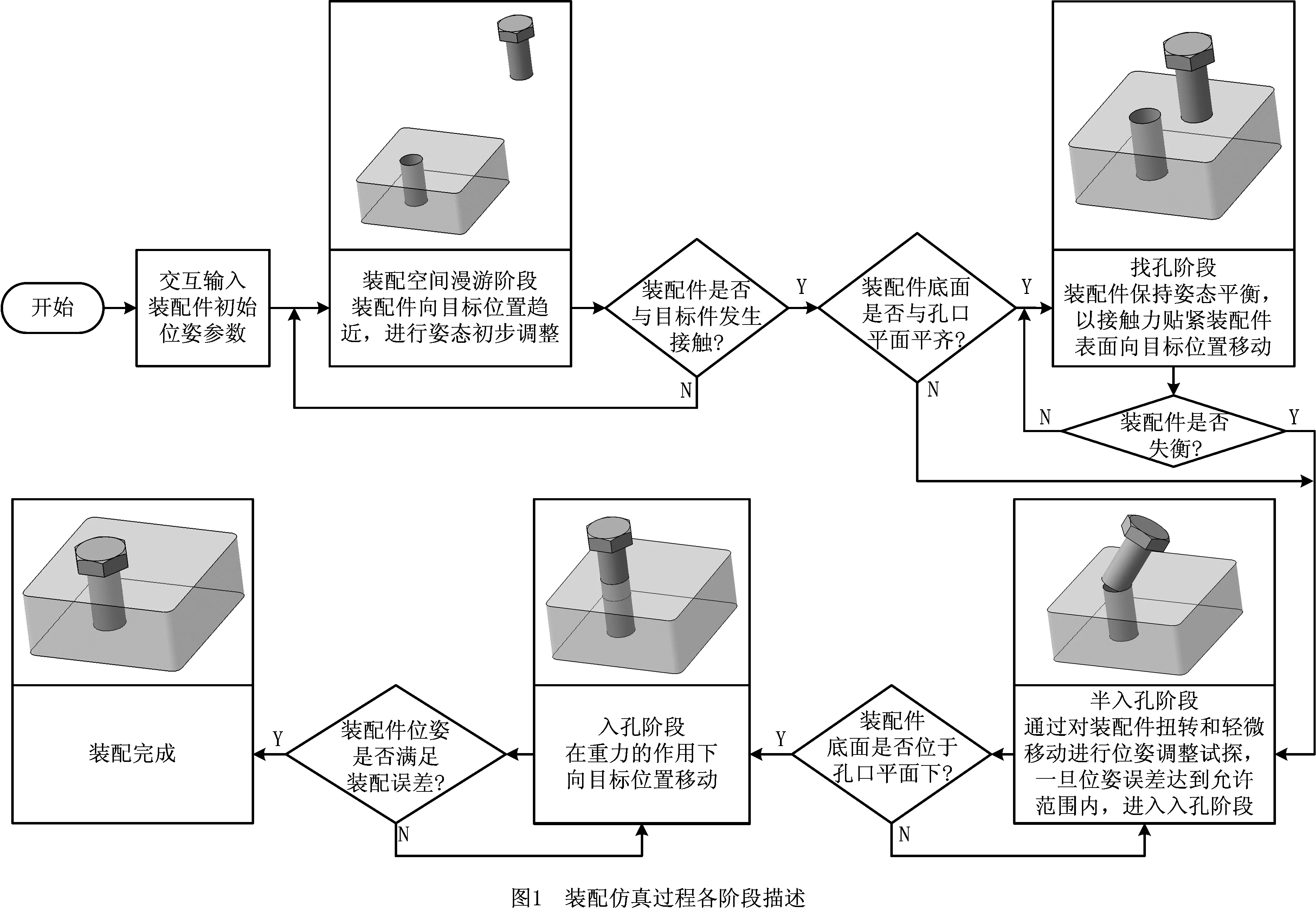
2 面向装配过程仿真的物体位姿描述方法及控制策略

为表达虚拟装配环境下物体的位置和姿态，需要在物体上固连一个坐标系，并给出该坐标系相对于参考坐标系的描述参数，物体位置由坐标原点表示，而对于物体姿态，传统的刚体运动学和动力学大多基于各坐标轴参数对物体的姿态进行描述，例如姿态旋转矩阵方法通过各坐标轴与参考坐标轴夹角的余弦值组成的3×3矩阵参数对物体姿态进行描述;姿态欧拉角方法通过将参考坐标系按照一定顺序绕相应的坐标轴以相应的欧拉角参数进行3次旋转得到当前姿态的方法对物体姿态进行描述。这些姿态描述方法用在刚体姿态表达方面虽然很灵活方便，但却需要复杂的几何运算和数学推导。实际上，装配者头脑中并不存在这些复杂的姿态参数，也不会根据这些参数去认知装配件的姿态。同时，一个坐标系中各个坐标轴方位之间是强耦合关系，调整一个坐标轴方位必然会牵连其他坐标轴发生转动，因此装配者不会依据这些基于坐标轴的姿态参数对装配件进行姿态调整。

实际上，装配者对物体姿态的认知是简洁直观的，更多的是基于坐标平面方位而不是坐标轴方位去认知物体姿态。这里以装配件的装配特征为例，对本文的姿态描述方法进行说明。如图2所示，O′X′Y′Z′为固连在装配特征上的随动坐标系，OXYZ为参考坐标系，为方便装配仿真，通常会将其固连在目标特征上。X′O′Y′平面过装配件质心，且与装配特征的底面平行，定义X′O′Y′平面为装配特征基准平面，X′O′Z′纵面为装配特征基准纵面，XOY平面为目标特征基准平面，XOZ纵面为目标特征基准纵面，通过基准平面方位和基准纵面方位可以完整定义一个物体的姿态。在实际装配作业中，装配者并不会一次同时处理过多姿态信息，为简化装配操作，装配者一般按照先基准平面后基准纵面的次序对物体姿态进行认知和调整。首先，由X′O′Y′平面与XOY平面的夹角误差β和交线LX′O′Y′确定X′O′Y′的方位，并以β为参数，垂直于LX′O′Y′旋转装配件来完成X′O′Y′平面的调整定位。然后，通过X′O′Z′纵面与XOZ纵面的夹角误差γ确定X′O′Z′的方位，并以γ为参数，垂直于O′Z′扭动装配件来完成纵面X′O′Z′的调整定位。

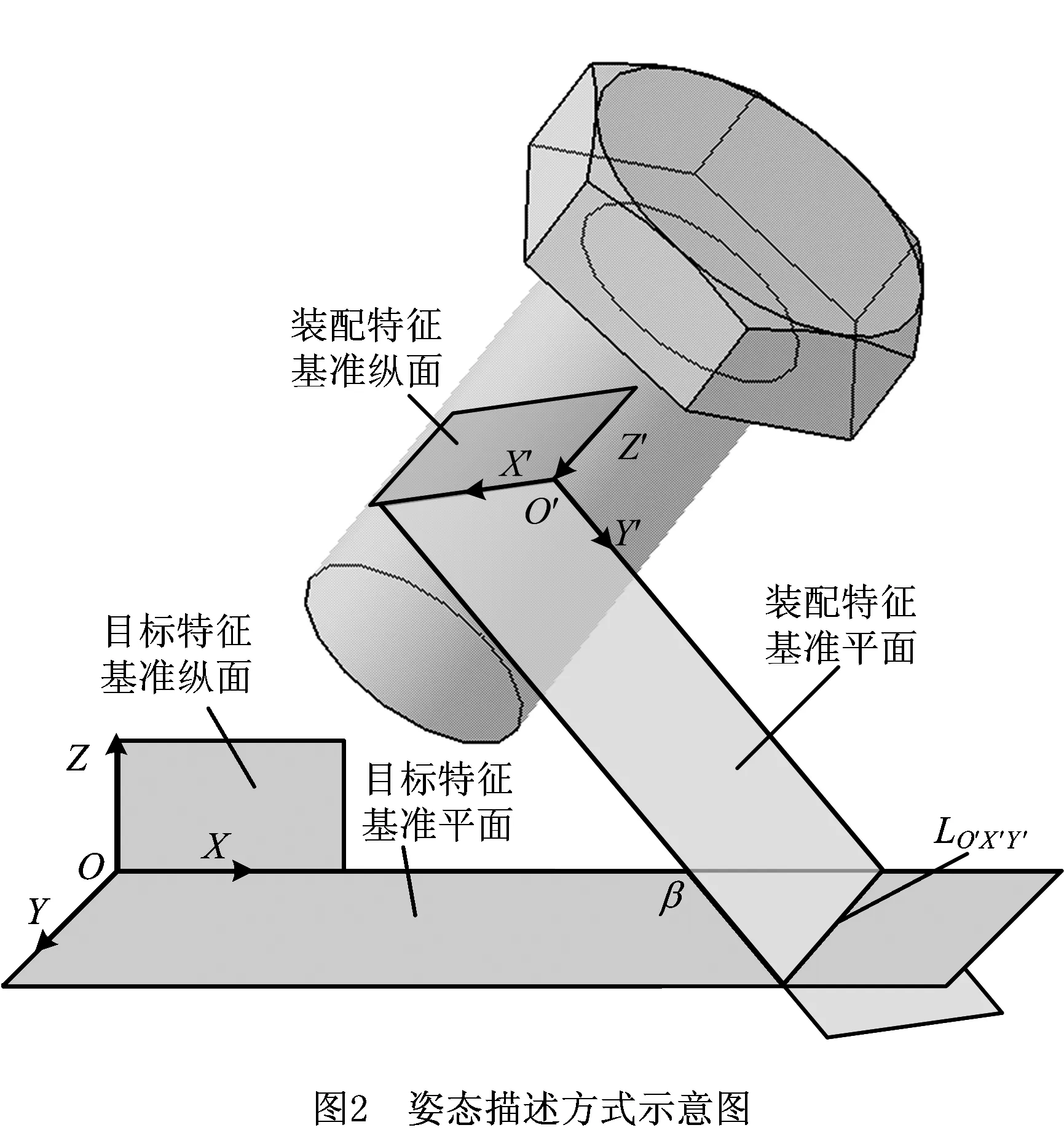
3 人机因素对装配引导定位的影响

为实现对装配件的引导和定位，装配者会根据目标特征的位置和姿态施加装配力和装配力矩来驱动装配件进行移动和姿态调整。但是由于目标特征的可视性条件(受目标特征在视域中的相对位置、视线角度等因素影响)不同，装配者对目标特征位姿信息的判断带有一定的误差。同时，人手施加的装配力和装配力矩并不绝对准确，其本身带有一些固有的模糊性和随机性，并且随着装配者舒适度的变差和疲劳度的增加(受装配者身体姿态、装配作业能量消耗等因素影响)，装配力和装配力矩的误差有加大的趋势。由于这些人机因素对装配件引导定位的影响，在实际装配过程中，装配力、装配力矩驱动的实际目标位姿与目标特征的真实位姿存在一定误差。本文将该实际目标位姿称为目标估计位姿，利用蒙特卡洛方法对其进行计算，如图3所示。

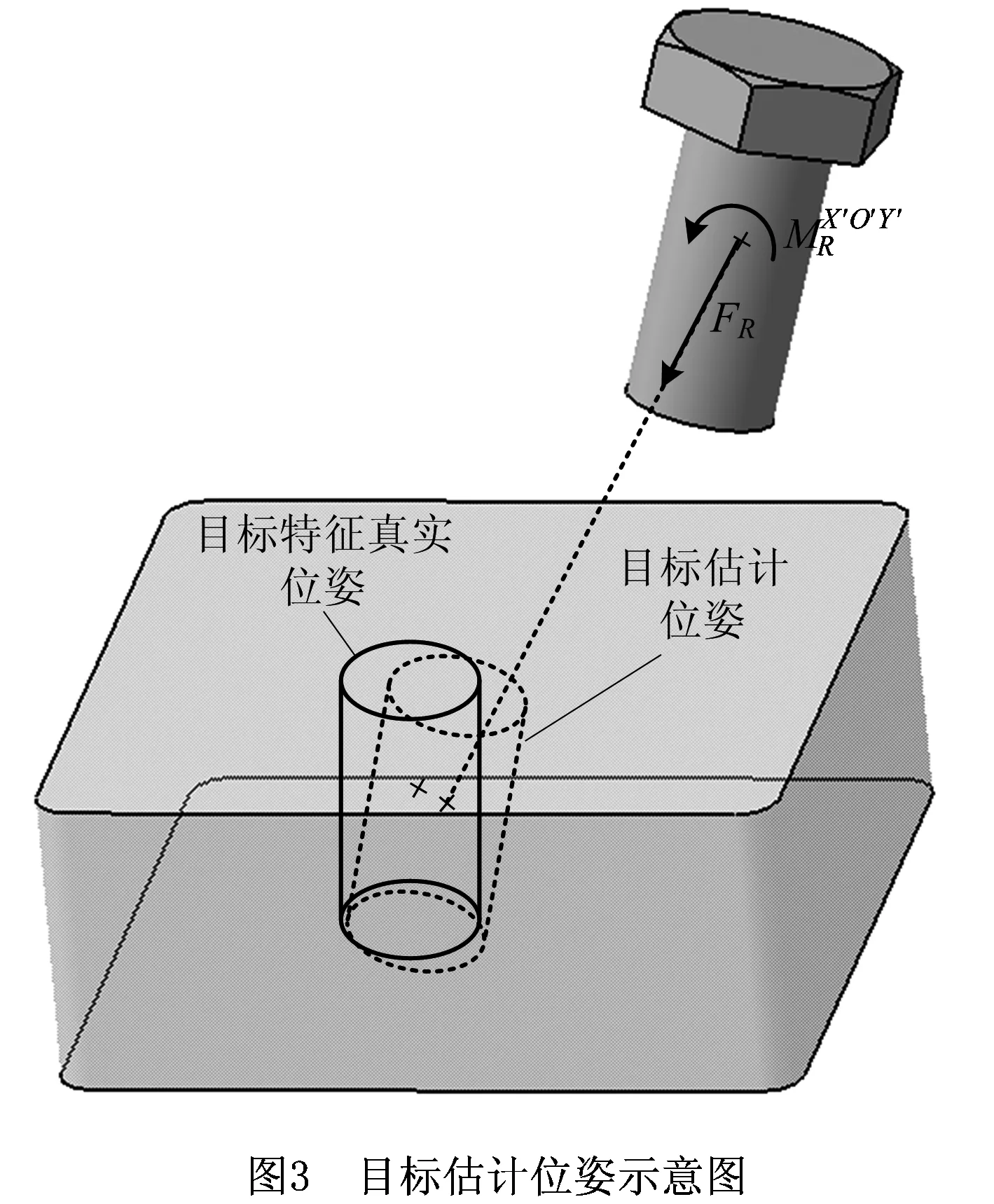
3.1 目标估计位置计算

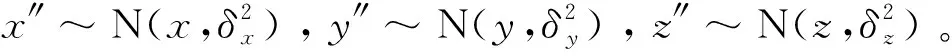
(1)

式中：Ex为位置采样点沿X轴的单边误差，ψ为人机系数，由可视性、舒适度、疲劳度等因素决定。计算人机系数时的关键是确定各影响因素的权重。参考木桶短板理论(木桶壁上最短的板决定了木桶的盛水量)，评估值越低的人机因素对人机系数总体评估值的影响作用越大，其在计算人机系数时所占的权重也越大。人机系数

(2)

式中：VI为可视性评估值，CO为舒适度评估值，TI为疲劳度评估值，取值范围均为[0，1]，取值方法参考笔者的前期研究[15]，也可由人机工程专家对装配任务进行评估后输入。

3.2 目标估计姿态计算

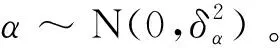
(3)

式中：Eα为目标特征基准平面估计姿态采样点单边误差，β为目标特征基准平面和装配特征基准平面夹角。目标特征基准纵面估计姿态的计算与此类似，不再赘述。

4 装配力与装配力矩计算模型的建立

4.1 装配空间漫游阶段

装配空间漫游阶段是指装配件从初始位姿运动到和目标件发生碰撞的过程，如图3所示。该过程实际上是装配件作为一个自由刚体，在装配力和装配力矩作用下进行位姿调整的过程。前期装配的主要任务是将装配件向目标件趋近，并对装配特征姿态进行初步调整。本文将装配件移动的过程近似为一个匀加速—匀速—匀减速的过程，如图4所示。图中：3个阶段的时间比例为2∶5∶3，移动速度vR可依据车间装配速度要求自主设定，路程SR指从装配件当前位置O′到目标估计位置O″的距离。

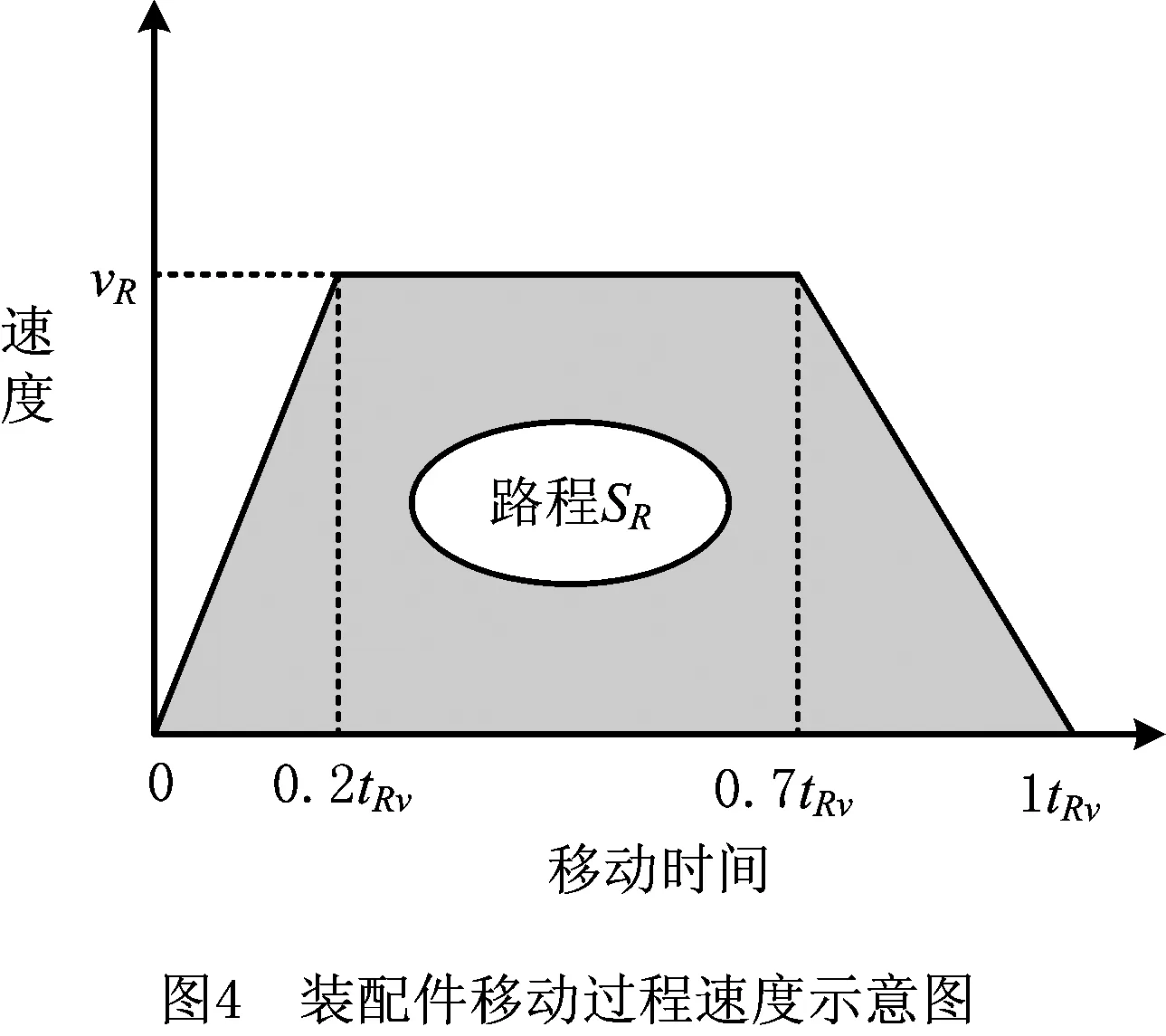
由运动学公式得

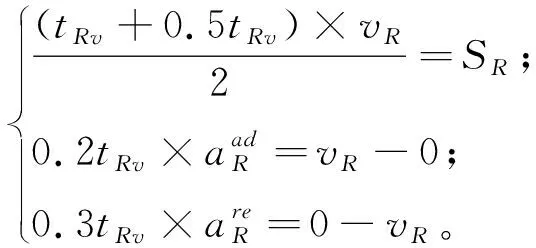
(4)

由牛顿第二定律得

FR+G=m·a。

(5)

联立式(4)和式 (5)求解FR，并将其在水平面和竖直方向投影得到：

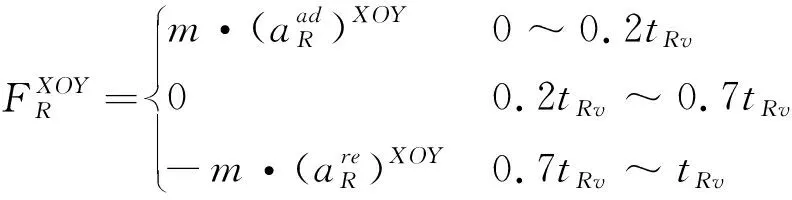
(6)

(7)

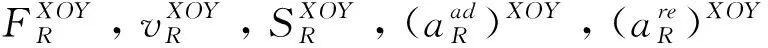
根据装配操作的一般习惯，装配者先完成装配特征基准平面的姿态调整，再进行装配特征基准纵面的姿态调整。以装配特征基准平面的姿态调整为例，为模拟人在现实中的装配操作，姿态调整目标选择为目标估计姿态基准平面，同样将该姿态调整过程近似为一个匀加速—匀速—匀减速的过程，类比式(6)的推导过程，得到：

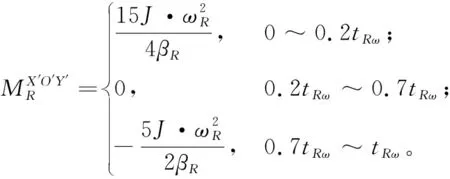
(8)

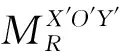
4.2 找孔阶段

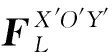
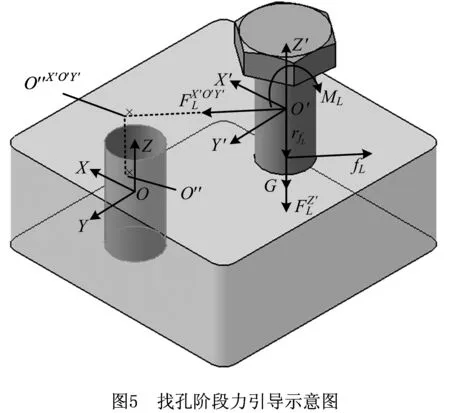
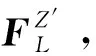
(9)

式中：G表示重力，A表示装配件和目标件接触面积，pmax表示装配件和目标件相对滑动时最大接触压强，可依据装配车间对零部件表面质量要求进行自主设定。

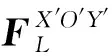
由运动学公式得

(10)

由牛顿第二定律得

(11)

联立式(10)和式(11)解得：

(12)

在装配件与目标件相对滑动的过程中，为使装配件的姿态保持稳定，需要施加装配力矩ML，根据空间力矩平衡条件，可得

ML+MfL=0,

(13)

解得

ML=-rfL×fL。

(14)

4.3 半入孔阶段

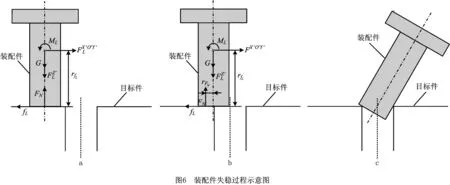
4.3.1 装配件失稳过程分析

在找孔阶段，装配件保持姿态平衡，克服摩擦力向目标位置滑动，如图6a所示。当装配件接近目标位置时，装配件和目标件的接触面积减小，接触力的作用点也会随之发生偏移，如图6b所示。而接触力作用点的偏移会产生附加的接触力矩，打破力平衡状态，即

FN·rFN+fL·rfL>ML，

(15)

从而造成装配件失稳，进入半入孔阶段，如图6c所示。

4.3.2 装配件的扭动

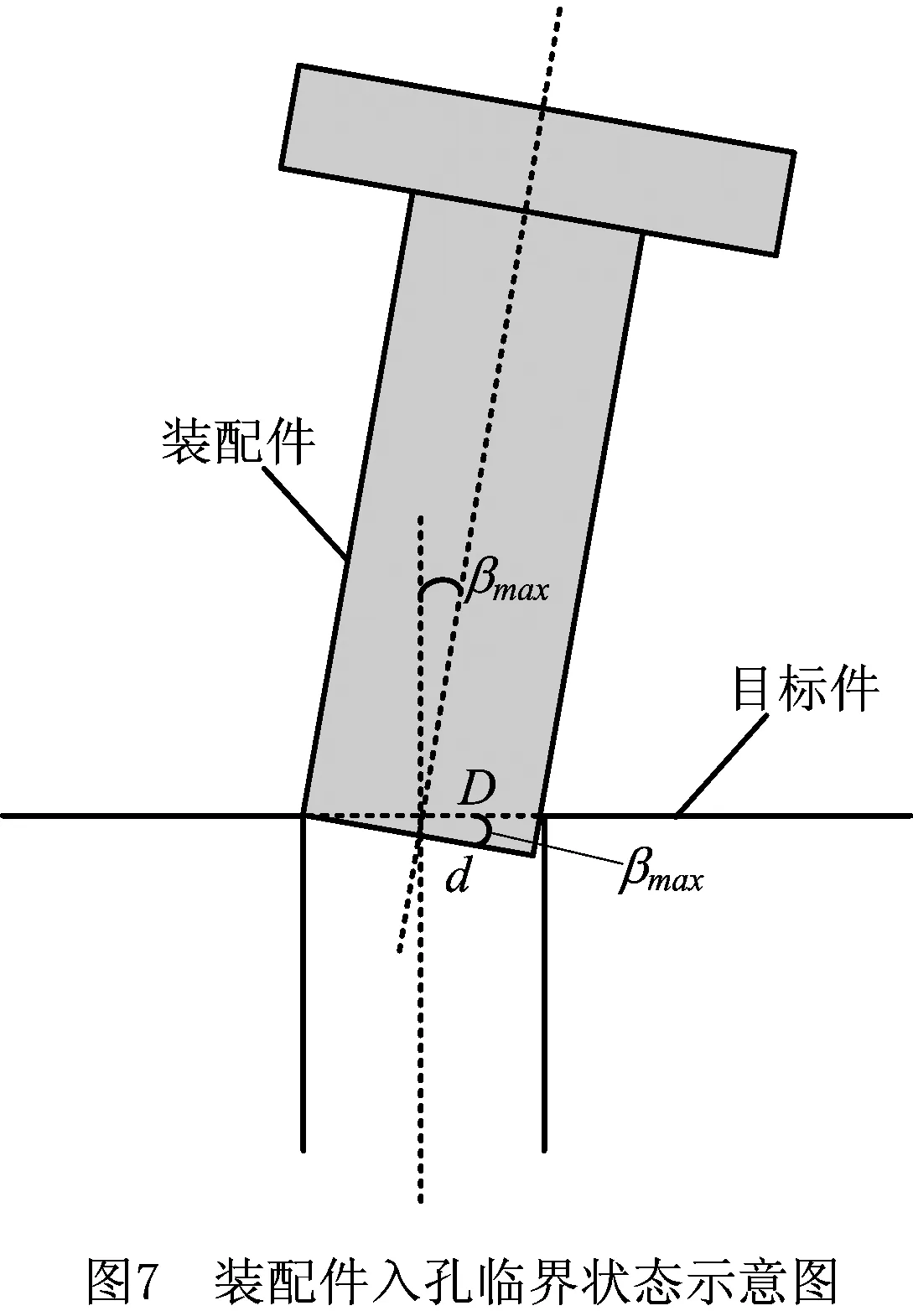
装配件要顺利过渡到全入孔状态，装配特征和目标特征的位姿误差需在一定范围内，为满足该条件，装配者将以扭动和轻微移动装配件的方式进行位姿调整试探。分析临界状态的几何关系，如图7所示，装配特征基准平面与目标特征基准平面最大误差角(亦是最大入插偏角)

(16)

式中：d为轴直径，D为孔直径。

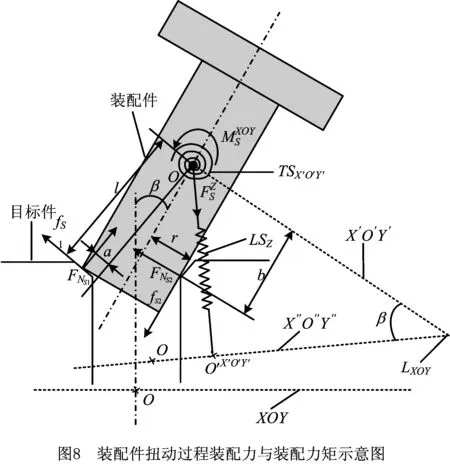
扭动装配件的目的是消减装配特征基准平面X′O′Y′和目标特征基准平面XOY的姿态误差，本文通过线性弹簧力学模型和扭转弹簧力学模型模拟该过程施加的装配力和装配力矩，如图8所示。角β为装配特征基准平面X′O′Y′和目标特征基准平面XOY的误差角(即入插偏角误差)，角β′为装配特征基准平面X′O′Y′和目标估计姿态基准平面X″O″Y″的误差角。

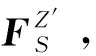
(17)

式中：O′O′X″O″Y″指装配件当前位置点O′与目标估计姿态基准平面X″O″Y″的距离，O′X″O″Y″为点O′在平面X″O″Y″的投影点。LSZ″的初始长度设置为0。

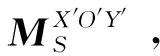
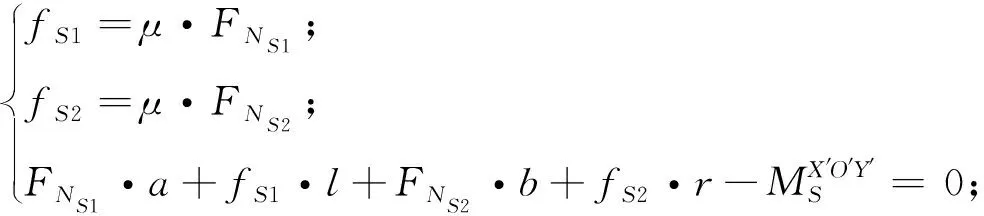
(18)

式中：FNS1,fS1分别为左侧接触点的接触力和摩擦力，FNS2，fS2分别为右侧接触点的接触力和摩擦力。

由此解得

(19)

通常取临界力矩的1.2倍确定扭转弹簧刚度KTSX′O′Y′，即

(20)

扭转弹簧的初始转角位置取目标估计姿态基准平面X″O″Y″处。

4.3.3 装配件的微移

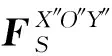
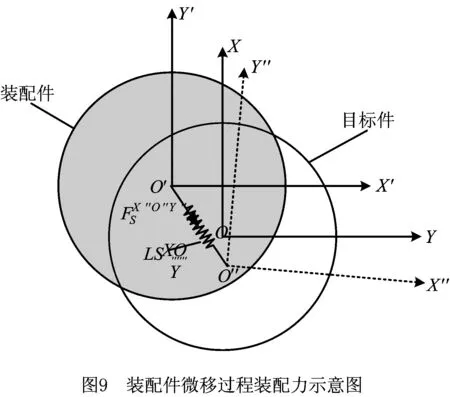
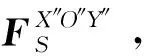
(21)

式中：(O′O″)X″O″Y″指矢量O′O″在X″O″Y″面投影的长度。LSX″O″Y″的初始长度设置为0。

4.3.4 装配件的微转

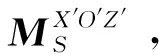
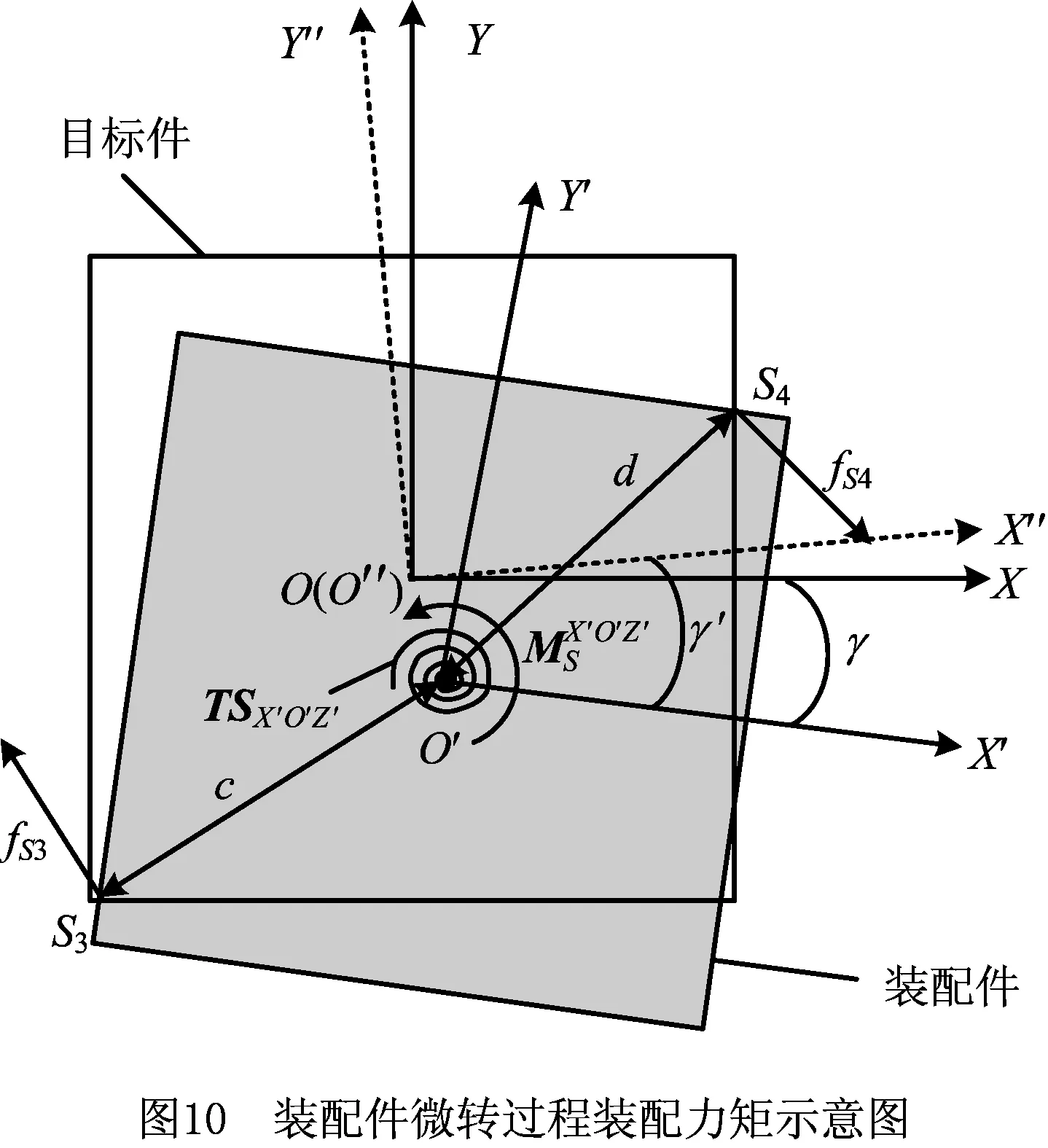
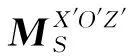
(22)

式中：FNS3为接触点S3处的接触力,FNS4为接触点S4处的接触力,γ′为装配特征基准纵面X′O′Z′和目标估计姿态基准纵面X″O″Z″的角度误差。扭转弹簧的初始转角位置设置在X″O″Z″处。

5 接触力的计算

接触力是由物体间相互碰撞接触而产生的相互作用力，与物体材质、相对速度和碰撞角度等因素有关。碰撞检测是虚拟环境下接触力计算的技术难点之一，本文结合层次包围盒法和文献[16]提出的基于精确几何模型的碰撞检测方法，对虚拟装配环境下的零部件进行碰撞检测。首先进行零部件包围盒层的碰撞检测，对发生干涉的包围盒所对应的零部件进行面片层碰撞检测，以获取发生碰撞的多边形；然后将检测结果映射到零件几何上，再根据发生碰撞位置处的零件几何公差属性信息计算碰撞阈值;最后依据碰撞阈值对零件间的碰撞情况进行精确判定，计算零件间的穿透深度和相对速度。基于上述碰撞检测结果，参考文献[17]所提的方法对接触力进行计算，接触力主要由零件间相互挤压而产生的弹性力和零件间相对速度而产生的阻尼力两部分组成。为了防止接触过程中发生阻尼力不连续的现象，定义阶梯函数，其形式为step(x,x0,y0,x1,y1)，计算方式为

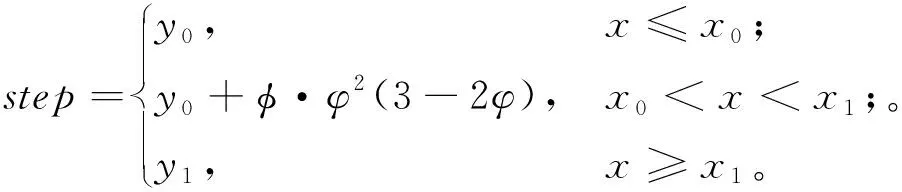
(23)

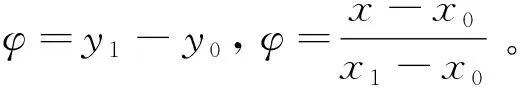
接触力

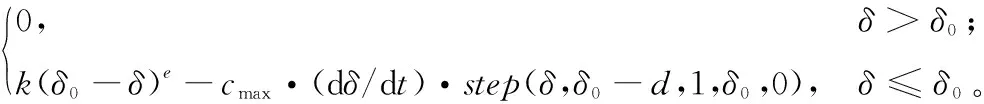
(24)

式中：δ0为发生碰撞物体的初始距离，δ为物体碰撞过程中的实际距离，d为最大嵌入深度，k为刚度系数，e为碰撞指数，cmax为最大阻尼系数，dδ/dt为物体间的相对运动速度。

6 装配仿真流程

6.1 动力学和运动学方程的建立

在每一仿真时刻，由程序自动建立装配件的牛顿—欧拉方程：

mai=FAi+∑Fi；

(25)

(26)

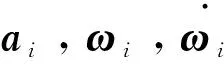
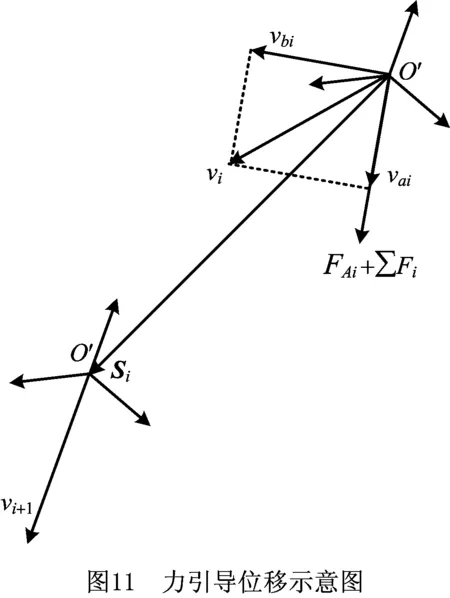
求解式(25)得出ai，代入式(27)所示的运动学公式，得出i～i+1时刻之间的位移矢量Si(如图11)：

(27)

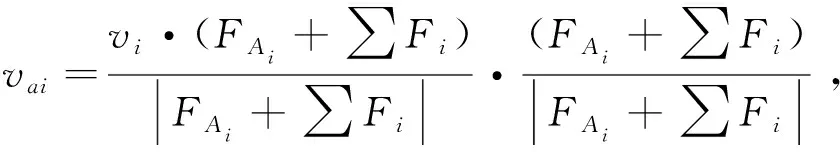
(28)

采用四阶龙格—库塔方法对式(26)进行求解，得出装配件的角速度、角加速度、绕X′，Y′，Z′轴的欧拉角θXi，θYi，θZi，进而得到姿态变换矩阵

(29)

式中：cXi是cosθXi的简写，sXi是sinθXi的简写，其他符号与此类似，不再赘述。由此可得，i时刻的位姿变换矩阵Ti=RiDi。

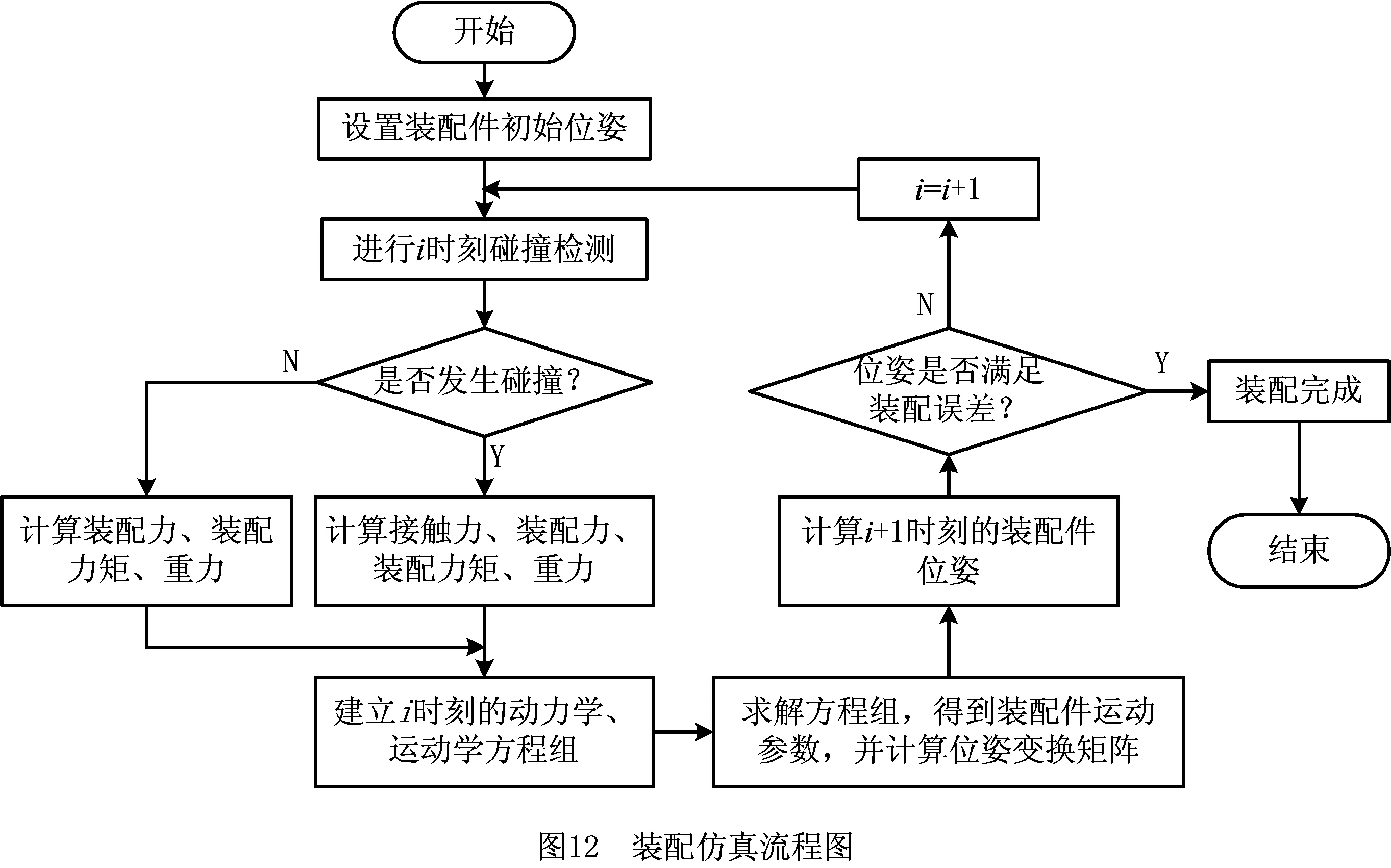
6.2 仿真流程

装配仿真的基本流程如图12所示。首先，由用户根据装配任务要求设置装配件的初始位姿，开始装配过程仿真，实时计算装配件在i时刻的装配力、装配力矩、重力、接触力，并由程序自动建立装配件的动力学、运动学方程组;然后，利用求解方程组所得的运动参数计算位姿变换矩阵Ti，进而获得装配件在i+1时刻的位姿Pi+1;最后判断Pi+1是否满足装配误差要求，如果满足则装配仿真完成，否则i=i+1，循环执行以上仿真操作。

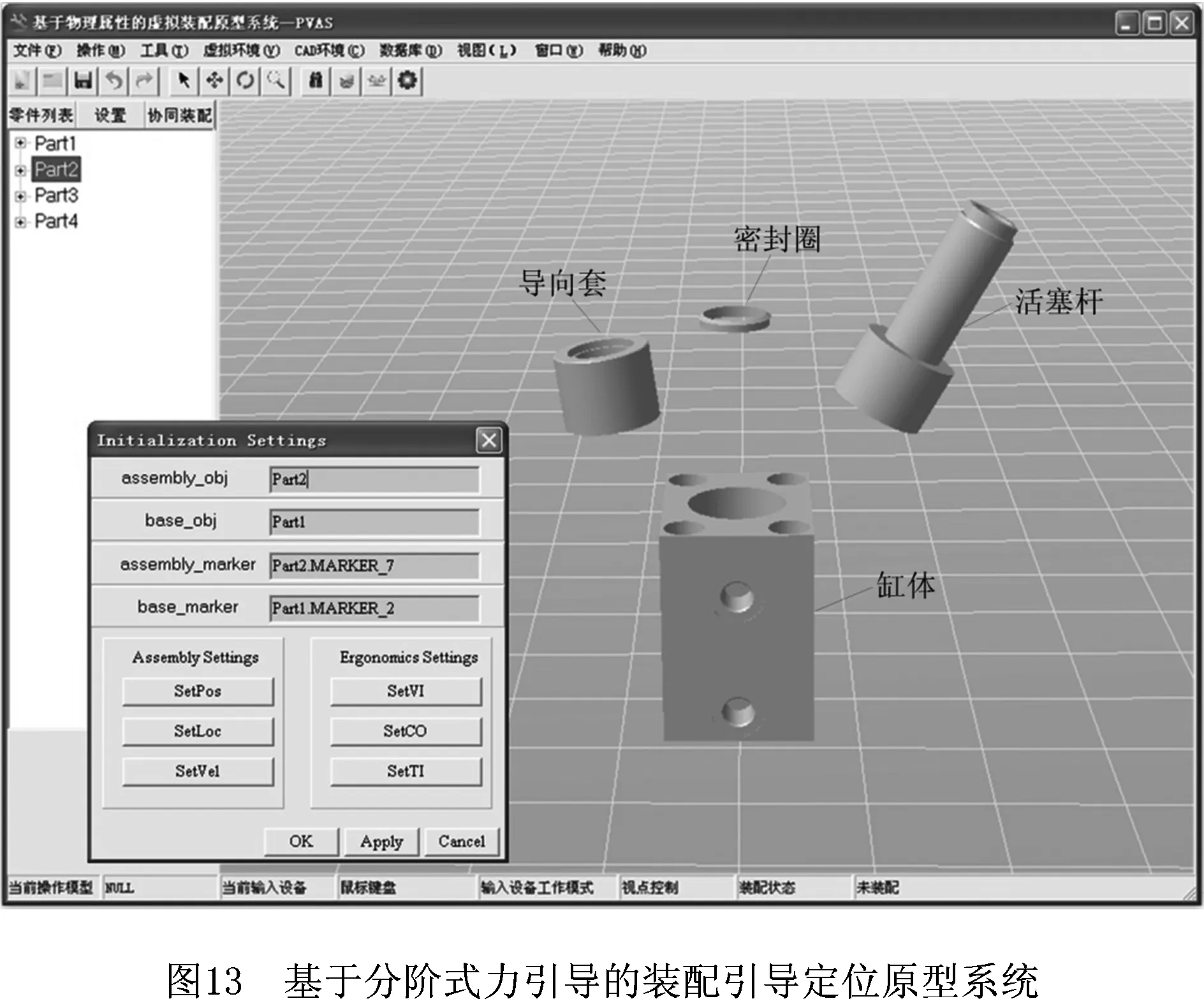
7 实例

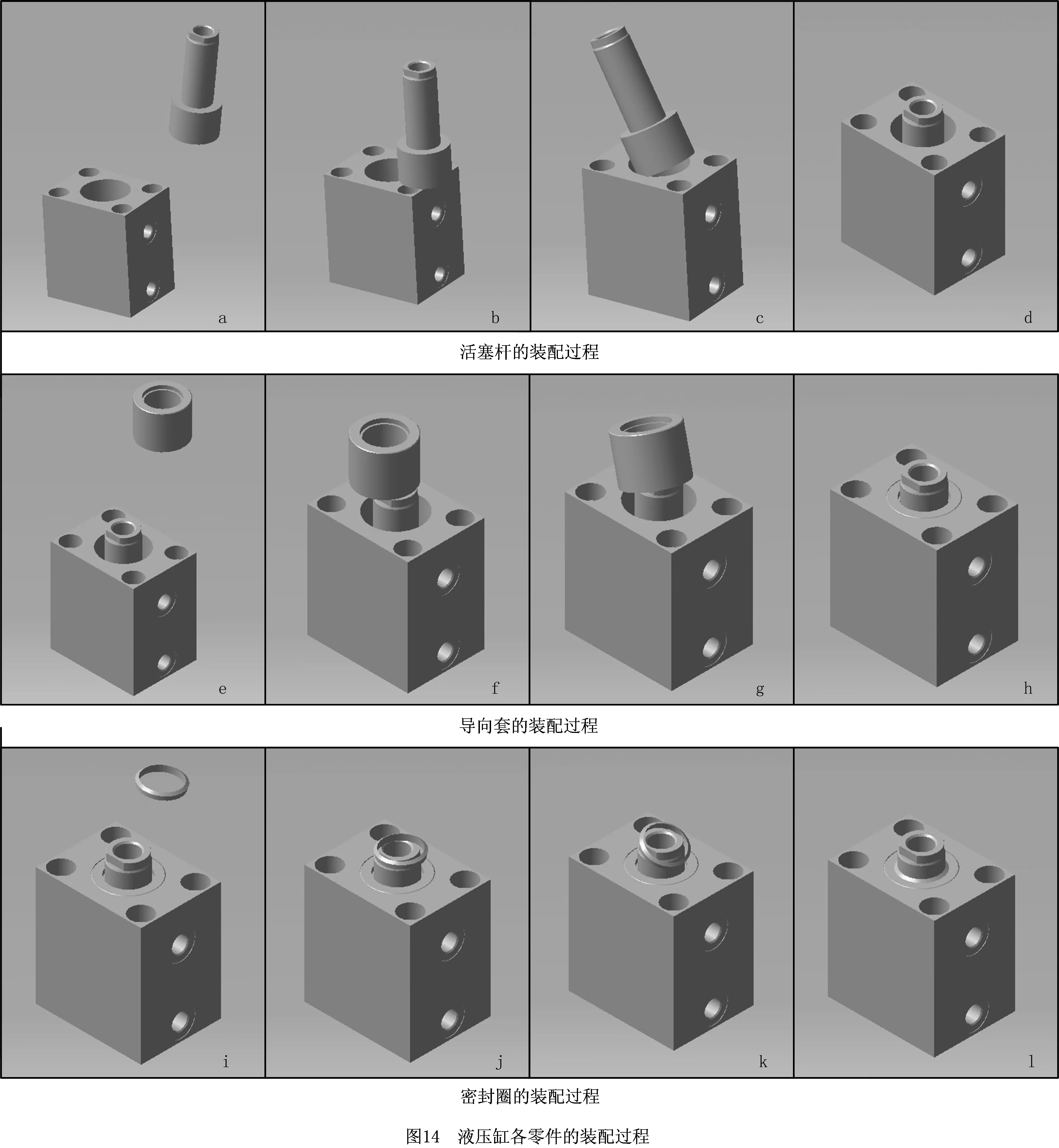
本文提出的基于分阶式力引导的装配定位方法在自主开发的虚拟装配原型系统中得到了应用，系统界面如图13所示。下面以某型液压缸的虚拟装配实例验证该方法的实用性，液压缸的主要零件如图13所示，各零件的装配过程如图14所示。以活塞杆为例说明具体装配过程，在每一仿真时刻按照上文所述方法计算装配力和装配力矩，由系统自动建立关于装配件重力、接触力、装配力及装配力矩的动力学方程组。通过对动力学方程求解得到下一时刻的位置、姿态、速度、角速度，求解位姿变换矩阵，对装配件进行位姿变换。从装配空间漫游阶段开始，活塞杆由初始位置向缸体移动，并在装配力矩的作用下进行姿态的初步调整(如图14a)；在与缸体发生碰撞后进入找孔阶段，活塞杆贴紧缸体表面克服摩擦力向缸筒运动(如图14b)；活塞杆失稳后进入半入孔阶段，在扭转弹簧力学模型和线性弹簧力学模型的作用下进行姿态的调整试探(如图14c)；在活塞杆与缸筒的姿态误差小于临界误差时，进入入孔阶段，在重力的作用下沿缸筒向目标位置运动，完成装配定位(如图14d)。

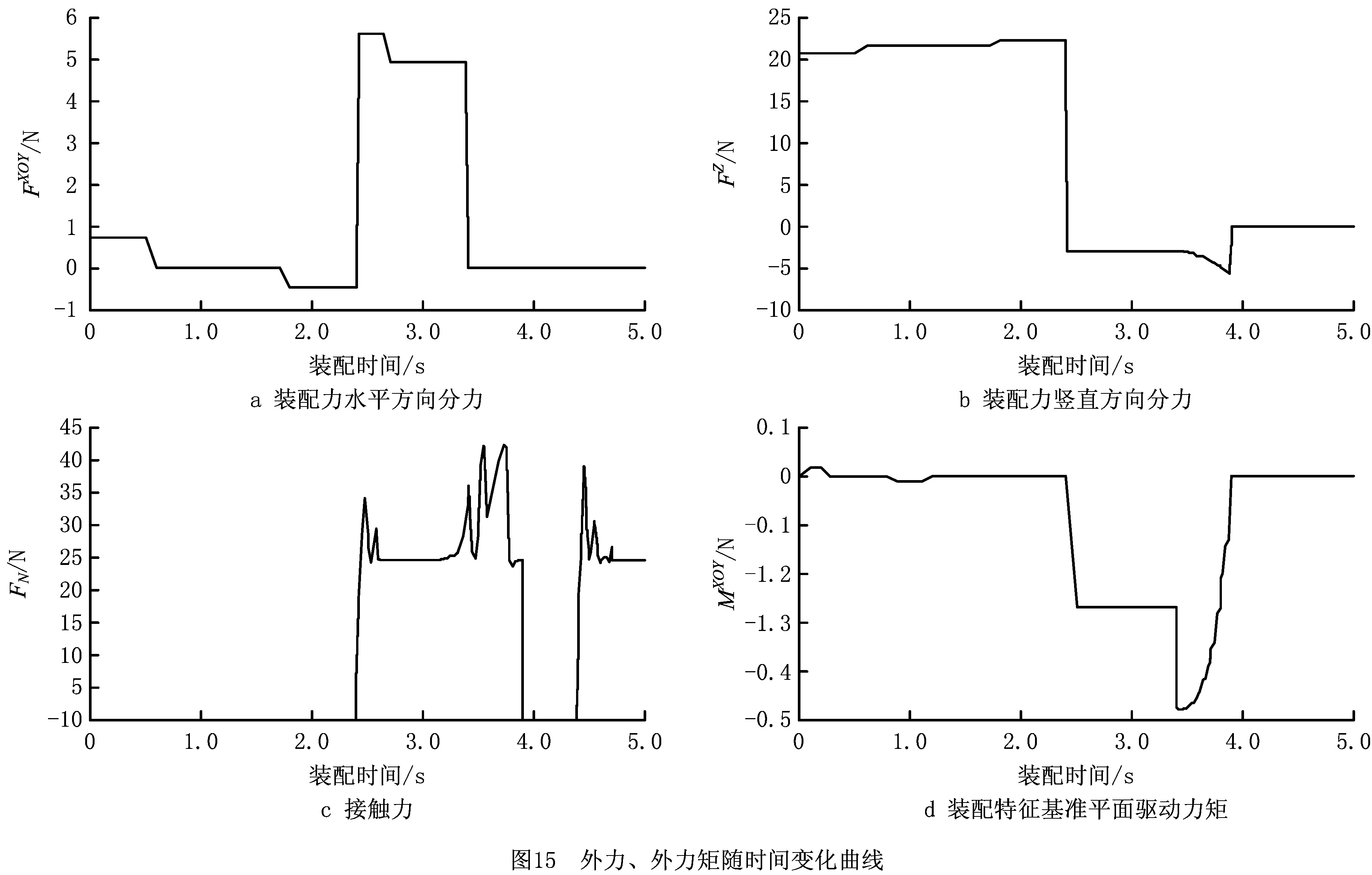
在活塞杆装配定位过程中，装配力水平方向分力FXOY、装配力竖直方向分力FZ、接触力FN及装配特征基准平面的驱动力矩MX′O′Y′起主导作用，其大小随时间的变化曲线如图15所示。

从图15可知：

(1)在装配过程的前2.4 s，接触力为0，活塞杆处于装配空间漫游阶段。此时，竖直方向的装配力远大于水平方向的装配力，说明活塞杆的重力是装配者能量损耗的主要原因。系统以较小的装配力矩对活塞杆的姿态进行初步调整。

(2)在2.4 s～2.6 s时，接触力出现波动变化，说明活塞杆与缸体接触碰撞。此后进入找孔阶段，活塞杆在装配力的引导下向目标位置滑动，系统通过施加装配力矩保持活塞杆运动过程姿态的稳定。

(3)在3.2 s～3.9 s时，活塞杆失稳，装配过程进入半入孔阶段。此时接触力波动变化较为剧烈，说明此时活塞杆姿态的调整主要靠装配力矩和零件间频繁相互接触碰撞的共同作用完成。装配力矩的曲线总体平缓，没有突变，显示系统对装配件姿态调整是自然、平稳的，符合客观规律。同时为避免活塞杆弹出，系统对其施加了竖直方向的装配力。

(4)在装配末期，装配力、装配力矩均为0，而接触力波动较大，说明接触力对零件最终的准确定位起主导作用。

8 讨论

8.1 人机因素对产品可装配性的影响

在Xeon CPU 3.60 GHz的PC机上，选取图13中的活塞杆作为装配对象进行装配测试。由于该装配作业任务的体能消耗较少，文中TI=0.95，对VI和CO分别取多组值，每组值进行30次实验，每次实验装配件均从同一初始位置和同一初始姿态开始运动，记录每次装配时间并计算平均装配时间，绘制曲线如图16所示。

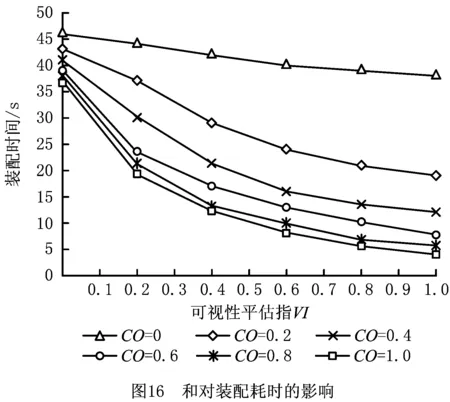
由图16可知：①当CO一定时，装配时间随着VI的增大而减少，这是因为装配区域的可视性越好，装配者对目标特征的位姿信息判断误差越小，装配定位越迅速准确；②当VI一定时，装配时间随着CO的增大而减少，这是因为装配者的操作姿态越舒适，施加装配力、装配力矩误差越小，装配耗时也越少；③当VI在0～0.2时，装配者对装配区域的观察极为模糊，装配定位的随机性极大，装配耗时很多；④当CO在0～0.2时，装配者的操作姿态非常勉强、不舒适，对装配件的控制带有很大的抖动误差，难以将装配件准确放置到位，装配效率极低；⑤在机电产品设计和装配环境布局设计中应重视可视性、可达性、舒适度等人机条件的改善，避免出现某一人机因素条件极端恶劣的情况，以保证装配作业安全、高效地进行。

8.2 结构因素对产品可装配性的影响

以活塞杆装配为例，对零件间的配合间隙和孔口倒角半径分别取多组值，每组值进行30次装配测试。为减少人机因素的影响，选取较为良好的人机因素条件VI=CO=0.85，计算平均装配时间，绘制曲线如图17所示。

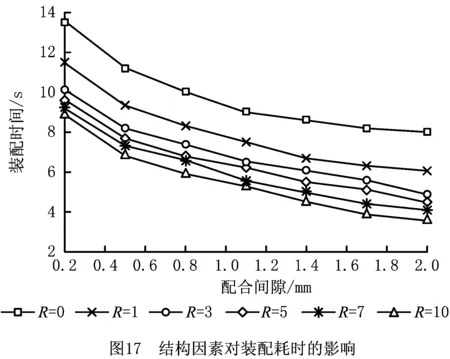
由图17可知：①当倒角半径一定时，装配时间随配合间隙的增大而减少，结合第4.3节的临界状态分析可知，配合间隙的增大使完成装配定位所允许的最大姿态误差增大，装配定位更加容易。②当配合间隙一定时，装配时间随倒角半径的增大而减少，这是因为倒角处的接触力有助于引导装配件向全入孔阶段过渡，使装配件的位姿调整更加准确，而较大的倒角半径可以使装配件尽早地接受这种接触力的引导，从而提高装配效率。

9 现实实验对比分析

以图13中的液压缸为装配对象分别进行虚拟装配实验和现实装配实验，通过对不同装配作业条件下装配效率进行分析对比验证本文所提方法对于实际装配的仿真程度。设置虚拟装配环境中各装配件的初始位姿与现实装配实验一样，虚拟装配所使用模型的几何参数和物理参数与现实装配对象保持一致。

实验过程如下：设置场景1～场景4中装配者距装配目标的距离分别为300 mm，400 mm，550 mm，700 mm，以使场景1～场景4的人机条件逐渐变差，装配作业难度逐渐增加。选择20名装配者，每位装配者进行15次装配实验，并记录装配时间。先对20位装配者的平均装配时间取平均值，以衡量各个装配场景条件下的实际装配效率，再对每位装配者的首次装配实验的装配时间取平均值。在每次现实装配实验中，装配者穿着数据衣，数据衣上布置有位移传感器，用以捕获装配者身体相关部位的位姿参数(如图18)，以便利用笔者前期研究的装配作业中人机因素量化评估方法[15]，对不同作业条件下的人机因素进行计算。将计算结果通过图13所示的对话框输入仿真系统中，系统将根据人机因素评估值实时计算装配力和装配力矩，利用动力学仿真对装配件进行引导和定位。通过以上操作完成各次现实装配实验所对应的人机条件下的虚拟装配仿真，参考现实装配实验中的数据处理方法对装配仿真时间取平均值，统计结果如图19所示。

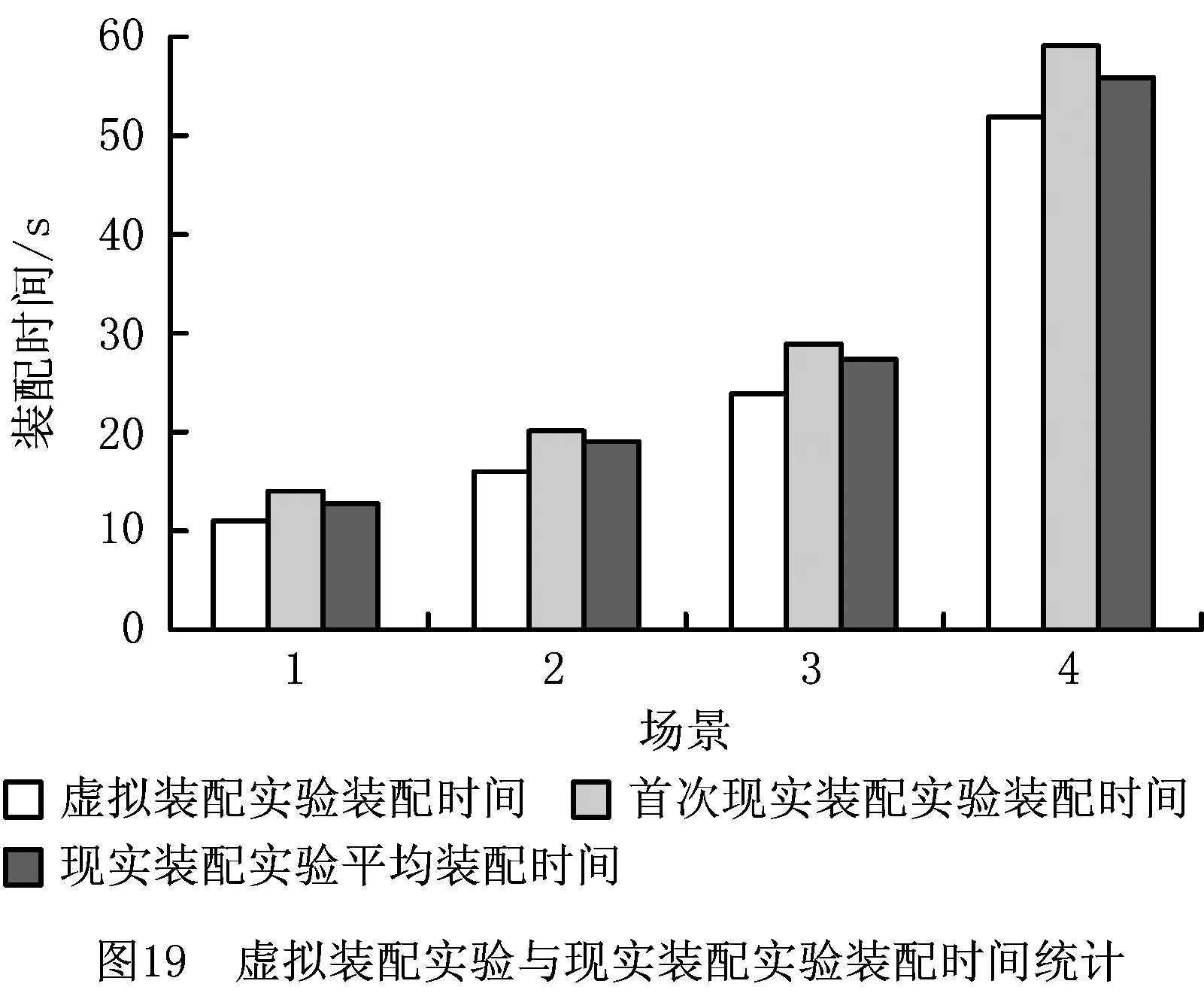
由图19可知：①对于不同的装配作业条件，虚拟装配时间和现实装配时间的变化规律大体一致，都是随着装配作业人机条件的变差而逐渐增加；②总体上，虚拟装配时间稍短于现实装配时间，主要是因为虚拟装配考虑的人机因素有限，没有考虑到其他更加细微复杂的因素(如装配者熟练程度、装配者力量等因素)；③在现实装配实验中，装配实验的平均装配时间少于首次装配实验的装配时间，这是因为随着装配次数的增加，装配者会逐渐熟悉装配操作，装配定位更加准确迅速，从而减少了装配时间。

10 结束语

为了避免由于交互设备精度不高而导致输入的装配力和装配力矩与真实装配意图不相符的问题，本文提出一种基于分阶式力引导的自动装配定位方法。传统桌面交互式装配由于没有考虑到装配过程中的人机因素和真实装配操作的特点，仿真出的虚拟装配过程与真实装配过程差距较大。本文分析了装配过程各阶段不同的施力特点，采取符合各阶段装配意图的施力策略对装配件进行引导定位；提出一种符合人对物体位姿实际认知特点的、简洁直观的物体位姿描述方法及控制策略；通过模拟人机因素对装配力和装配力矩的影响，将人机因素融入产品装配仿真过程中，以反映人机条件的优劣对产品可装配性的影响，提高装配过程仿真的真实感与可靠性。在本文工作的基础上，下一步的研究重点是将更多的人机因素融入产品的装配仿真过程中，如目标位置可达性和装配操作熟练度，并量化分析产品的可装配性。