基于混合优化算法的飞机总装脉动生产线平衡问题
潘志豪,郭 宇,查珊珊,章诗晨,王 彬
(1.南京航空航天大学 机电学院,江苏 南京 210016;2.北京卫星制造厂,北京 100190)
0 引言
随着我国航空产业的加速发展,军民各型飞机的生产订单快速增长,产品需求日趋多样化。在这一背景下,为解决传统的飞机总装固定站位生产模式中存在的装配效率低、生产现场混乱、质量难保证[1]等不足,各生产厂商将装配效率更高、产品质量更稳定的移动生产模式应用于飞机总装生产线。现有飞机总装的移动生产模式主要分为连续移动式和脉动式,其中脉动生产模式相对于连续移动生产模式具有生产柔性更高、产线运行更平稳、任务划分更合理等优势,能够更好地应对多变的生产需求和复杂的飞机构型。目前脉动生产模式已经在阿帕奇、F-35和波音787等飞机的总装中成功应用,极大地提高了飞机总装的生产能力和经济效益[2]。脉动生产模式在飞机总装中的成功应用离不开合理的生产线平衡方案,因此有必要结合飞机总装以及脉动生产模式的特点开展飞机总装脉动生产线平衡问题(Aircraft Pulse Assembly Line Balancing Problem, APALBP)的研究工作。
由于移动生产模式应用于现代飞机总装的时间较短,APALBP的相关研究文献数量较少,亟需进一步深入研究。其中Ríos等[3]以作业负载平滑为优化目标,通过仿真优化获取飞机总装线平衡优化结果;徐剑等[4]借助面向对象分层赋时Petri网建立飞机总装生产线模型,并基于该模型运用启发式方法对第二类装配线平衡问题进行优化求解;张超等[5]通过粒子群算法对第二类飞机总装移动生产线平衡问题进行优化求解,并借助仿真软件进行结果分析。相关研究主要基于简单装配线平衡问题(Simple Assembly Line Balancing Problem, SALBP)和一般装配线平衡问题(General Assembly Line Balancing Problem, GALBP)模型对飞机总装线进行平衡优化,而未针对性地构建APALBP模型,所得平衡优化结果难以有效反映飞机总装的实际生产情况。为提高研究的应用价值,本文针对飞机总装脉动生产线多工种协同装配以及多区域并行作业等特点建立多目标多约束的APALBP数学模型,从而确保基于该模型的飞机总装脉动生产线平衡优化结果的有效性。
为获取生产能力和经济效益综合提升的平衡优化结果,将装配线平滑指数最小和人员总数最少作为飞机总装脉动生产线平衡优化的目标,同时根据生产线升级改造的实际需求和四类装配线平衡问题的特点[6],选择E类飞机总装脉动生产线平衡问题(APALBP-E)为具体研究对象。其中因为装配线平衡问题属于NP-hard问题,同时E类装配线平衡问题(Assembly Line Balancing Problem Type E, ALBP- E)中装配节拍和站位数量均不确定,使得目标函数具有多极值特点,进一步提高了优化求解的难度,所以传统的精确求解算法难以在有限时间内获取高质量的优化结果,需采用近似求解算法进行优化求解。近年针对ALBP-E优化方法的研究有:Masitah等[7]通过离散粒子群算法优化求解多目标E类单边装配线平衡问题;Wei等[8]改进了E类单边装配线平衡问题数学模型,并通过启发式算法优化获取优化结果;Zacharia等[9]运用改进遗传算法优化求解模糊作业时间E类单边装配线平衡问题。上述优化求解方法主要是将ALBP-E分解为多个第二类装配线平衡问题并依次进行求解,导致算法的求解的效率低下且效果不佳。为提高ALBP-E求解效率和结果质量,本文设计一种混合优化算法对APALBP-E进行优化求解,在求解过程中主要通过动态搜索算法提高算法的求解效率和结果质量,并通过改进种群个体距离和莱维飞行距离计算方法来提高第二类非支配排序遗传算法(Non-dominated Sorting Genetic Algorithm-Ⅱ, NSGA-Ⅱ)和布谷鸟搜索(Cuckoo Search, CS)算法的寻优能力。
本文对飞机总装脉动生产线的特点和平衡优化需求进行分析,并根据分析结果建立多目标多约束的APALBP-E模型,同时针对模型特点设计一种混合优化算法进行优化求解。最后通过标准案例测试以及应用案例分析,证明本文算法性能优异且能够有效求解APALBP。
1 飞机总装脉动生产线平衡问题描述
飞机总装脉动生产线的特点有:①在整线装配中产品按节拍脉动式向前移动,在作业站位中产品采取类似固定站位装配的作业方式,如图1所示;②飞机由多系统组成且体型较大,各作业任务在站位中特定区域进行,根据本文的应用案例作业区域划分为10个区域,如图1站位5所示;③飞机装配自动化程度较低,并涉及多个技术领域,各作业任务需由相应工种人员进行。
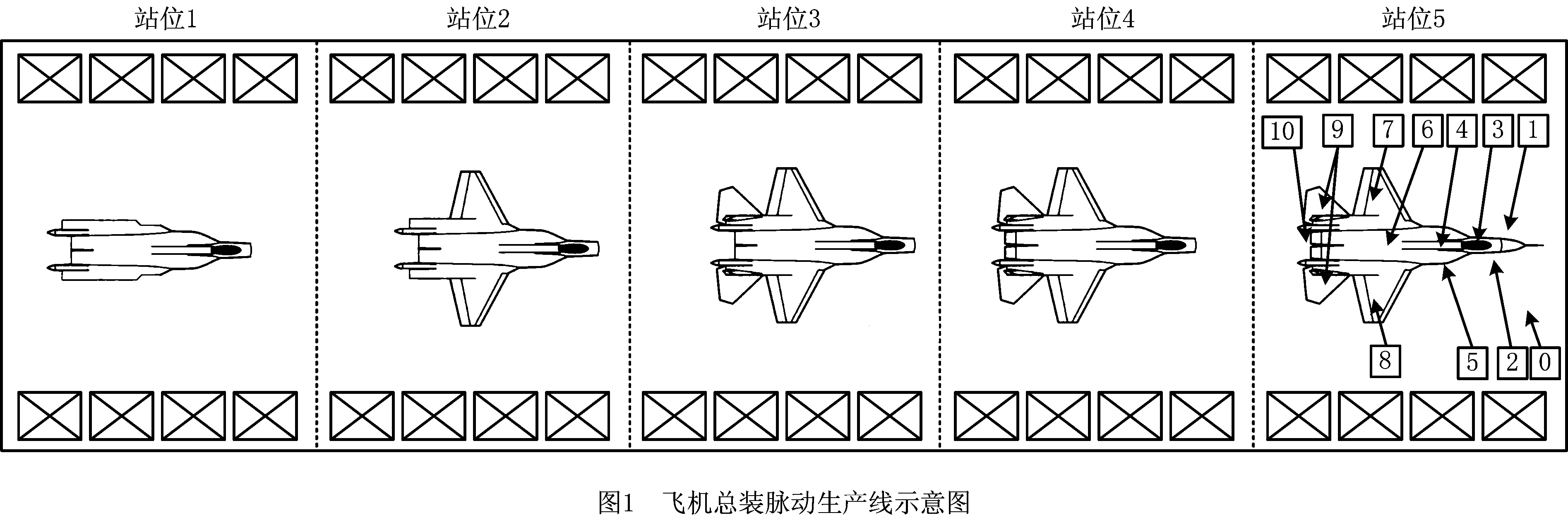
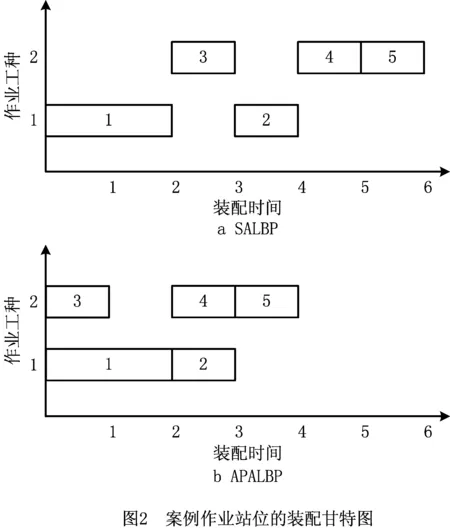
根据以上特点对APALBP提出以下假设:①作业任务装配时间确定;②所有任务都必须被分配到作业站位中;③人员被划分为多个工种,各工种仅能参与相应的作业任务;④同工种的人员装配作业熟练度一致;⑤各作业站位间不进行人员流动;⑥在作业站位内将装配空间划分为多个作业区域;⑦在作业站位中满足装配先后顺序约束和作业区域互不干涉的约束条件下,允许不同工种参与的装配任务并行作业,以5作业任务2工种的某作业站位为例,其中一个可行装配序列根据SALBP的假设获得的装配甘特图,如图2a所示,而根据APALBP的假设将作业站位的装配空间划分为两个作业区域,其中作业任务1,4的作业区域为1区域,作业任务2,3,5的作业区域为2区域,按照假设⑦可以得到作业站位的装配甘特图,如图2b所示,作业任务1和3、2和4并行装配。
2 飞机总装脉动生产线平衡问题模型构建
为进一步挖掘飞机总装脉动生产线的生产能力,提高生产线的装配效率和人员利用率,建立APALBP模型,并考虑人员工种约束和作业区域约束。
2.1 变量定义
n为装配作业任务数量;
m为装配线站位数量;
mmin为允许站位数量的下限;
mmax为允许站位数量的上限;
o为装配线工种数量;
a为装配作业区域数量;
i为装配作业任务序号,i=1,2,3,…,n;
j为装配线站位序号,j=1,2,3,…,m;
k为装配线工种序号,k=1,2,3,…,o;
l为装配作业区域序号,l=1,2,3,…,a;
si为作业任务的开始时间;
ci为作业任务的完成时间;
ti为作业任务i的装配时间;
pi为作业任务i的参与人员数量;
CT为装配线装配节拍;
PK(i)为作业任务i同工种的前一作业任务;
PL(i)为作业任务i同作业区域的前一作业任务;
G为装配作业任务优先关系集合;
2.2 目标函数
本文模型为最小规划模型,为获取装配效率和人员利用率最优的装配线方案,选取平滑指数和作业人员总数作为APALBP的目标函数。
(1)平滑指数
平滑指数(SI)反映各作业站位空闲时间的离散程度,用以评价生产线的装配效率,
(1)
式中Tj为作业站位j的总装配时间。
(2)作业人员总数
作业人员总数(SN)反映装配线的人员配置情况,用以评价生产线的人员利用率,
(2)
式中Pjk为作业站位j中工种为k类的作业人员总数。
2.3 约束条件
根据飞机总装脉动生产线的特点以及平衡问题的假设建立相应的约束条件,约束条件的数学表达如下:
cPK(i)≤si,i=2,3,…,n;
(3)
cPL(i)≤si,i=2,3,…,n;
(4)
ci=max(cPL(i),cPK(i))+ti;
(5)
Tj=max(ci·xij),i=1,2,…,n;
(6)
Tj≤CT,j=1,2,…,m;
(7)
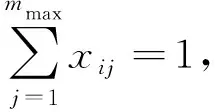
(8)
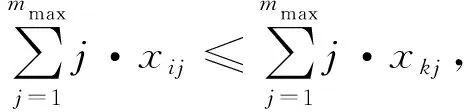
(9)
(10)
Pjk=max(pi·xij·yik),i=1,2,…,n。
(11)
其中:式(3)表示作业任务必须在同工种的前一任务完成以后才能开始装配;式(4)表示作业任务必须在同作业区域前一任务完成以后才能开始装配;式(5)表示作业任务装配完成时间为最早开始时间加装配时间;式(6)表示作业站位的所有作业任务完成时间为作业任务完成时间的最大值;式(7)表示作业站位的所有作业任务完成时间不能大于装配节拍;式(8)表示每个作业任务只能被安排在一个作业站位;式(9)表示各作业任务互相之间的装配先后顺序关系;式(10)表示在装配线中各作业区域一定会有作业任务进行装配;式(11)表示同站位中各工种的人数取该工种在该站位中单作业任务参与人数的最大值。
3 多目标多约束优化模型的求解算法及其性能测试
3.1 多目标多约束优化模型的求解算法设计
针对所建APALBP-E模型,设计一种混合优化算法进行求解。该算法混合改进的NSGA、NS算法以及动态搜索算法,其中改进的NSGA优化生产线装配序列,NS算法寻找装配线的最优站位数量,动态搜索算法则在多重解码过程中寻找各装配序列对应的最优站位数量和装配节拍,图3所示为混合优化算法的运行流程图。
3.1.1 编码和解码
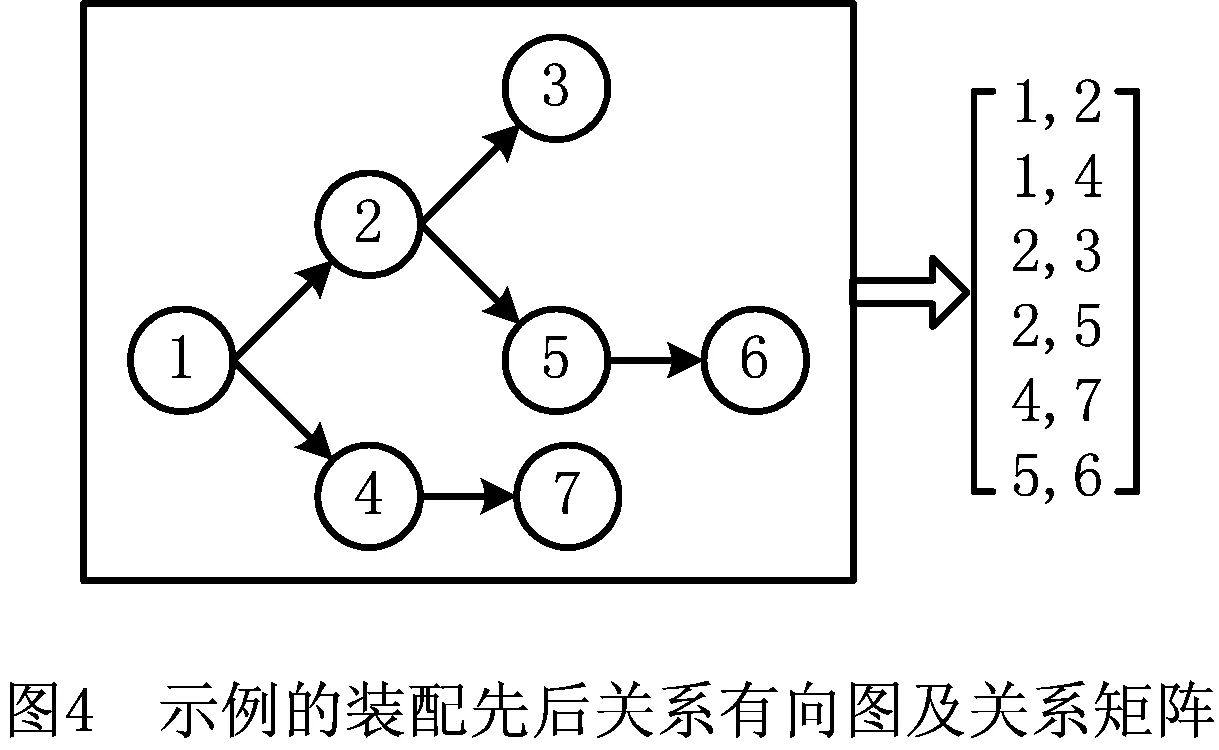
在个体的编码上采用面向装配序列的编码方式[10],该编码方式保证优化算法能够完全搜索APALBP的装配序列空间,但种群中会出现不满足约束条件的个体编码。以标准测试案例Mertens为示例,按照面向装配序列的编码方式可以得到示例编码{1,3,2,4,6,7,5},但由图4左图中的案例装配先后关系有向图可知,当前编码不满足装配先后顺序约束,需根据图4右图中的装配先后关系矩阵对编码从左向右依次进行约束检查和次序调整,示例编码经调整后得到编码{1,2,3,4,7,5,6},满足装配先后顺序约束。
因为所建模型为APALBP-E模型,在ALBP-E中装配节拍和站位数量均未知且二者相互影响,需要同时搜索二者的求解空间,其中站位数量的求解空间明显小于装配节拍的求解空间,所以图3中的装配序列解码采用确定站位数量的第二类SALBP(SALBP-Ⅱ)解码方法,其流程如下:
步骤1获取站位数量种群中与当前装配序列个体对应的站位数量m。
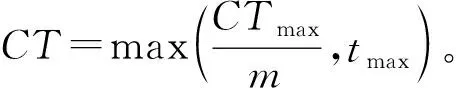
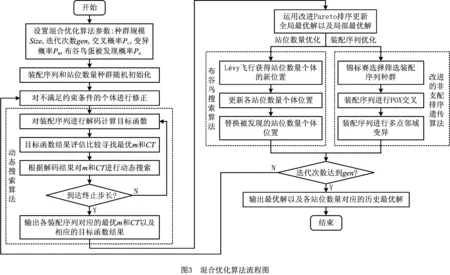
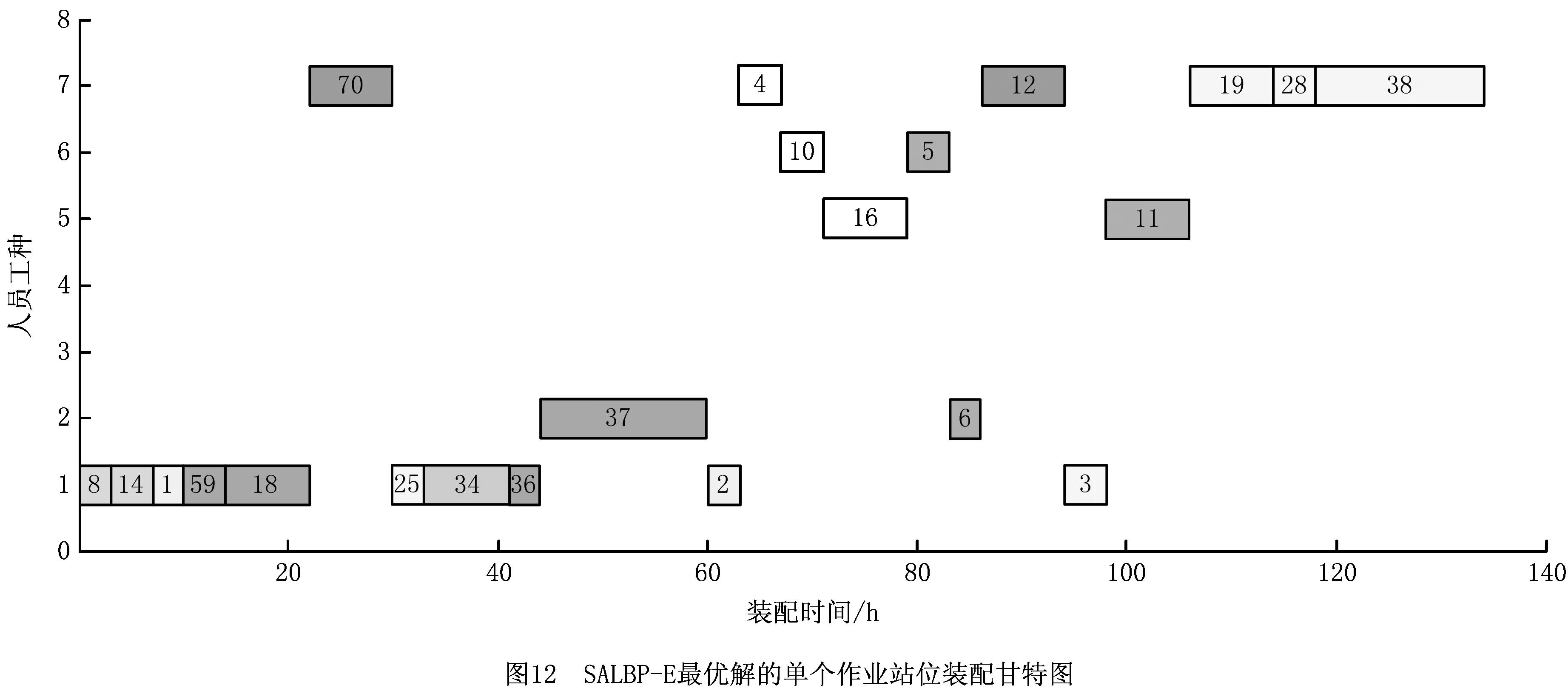
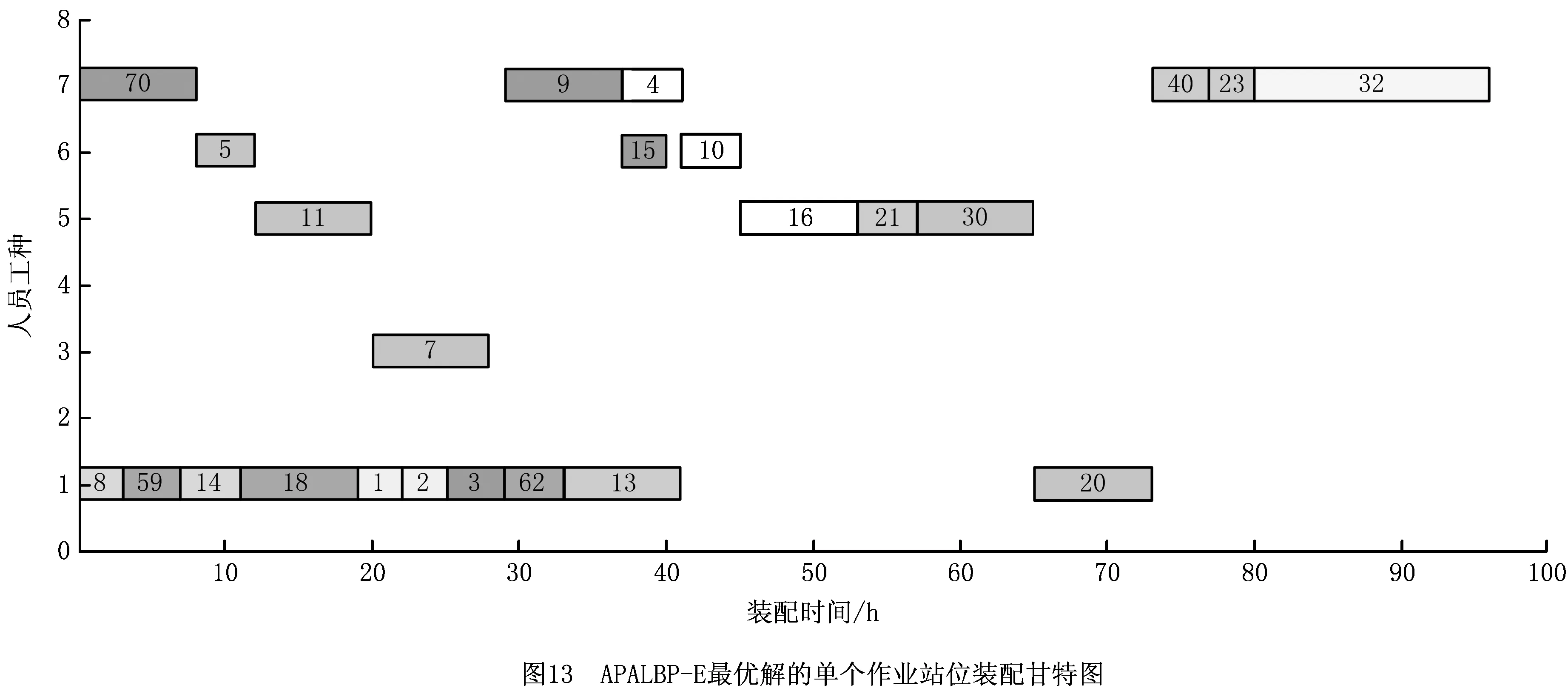
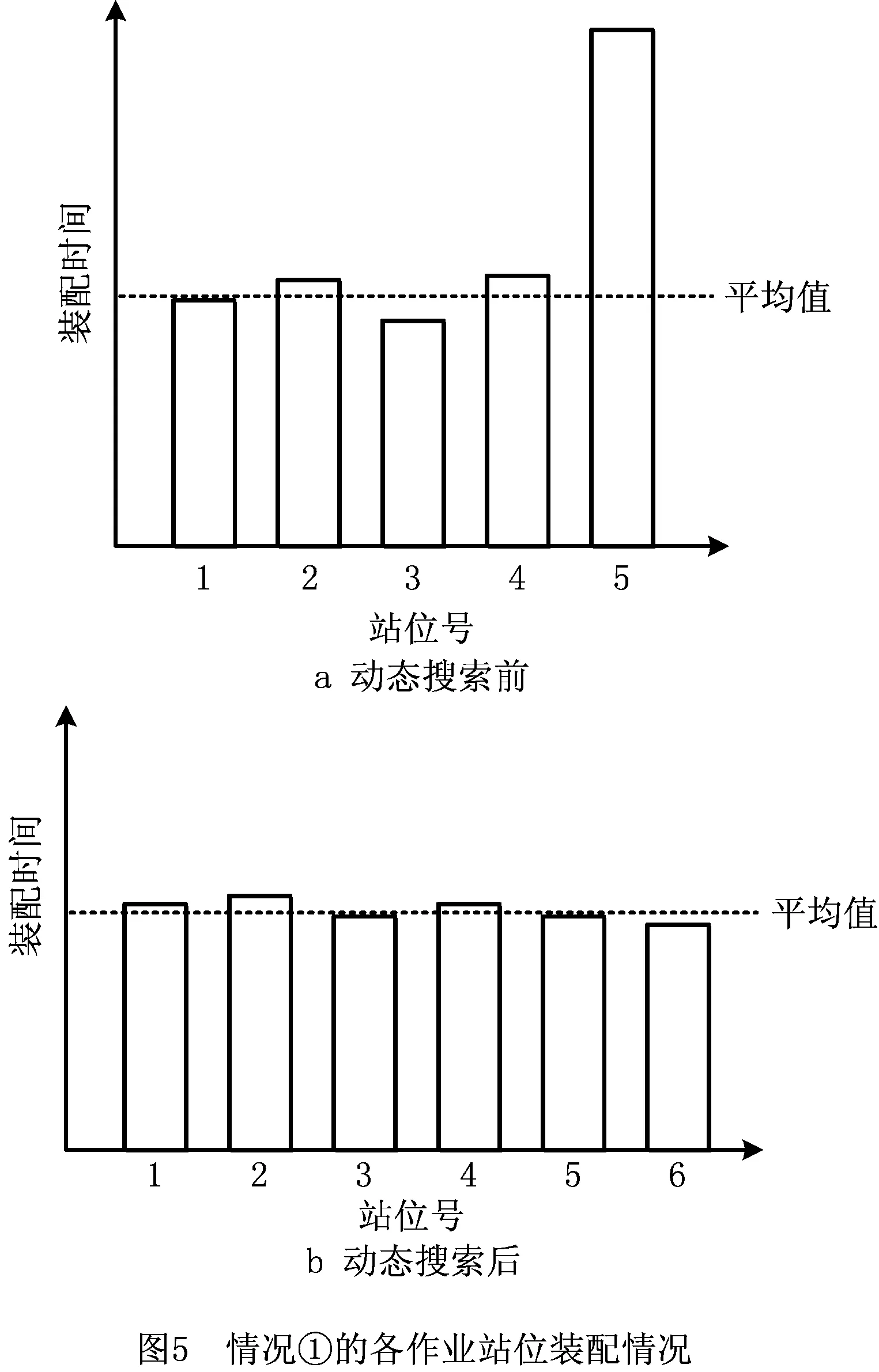
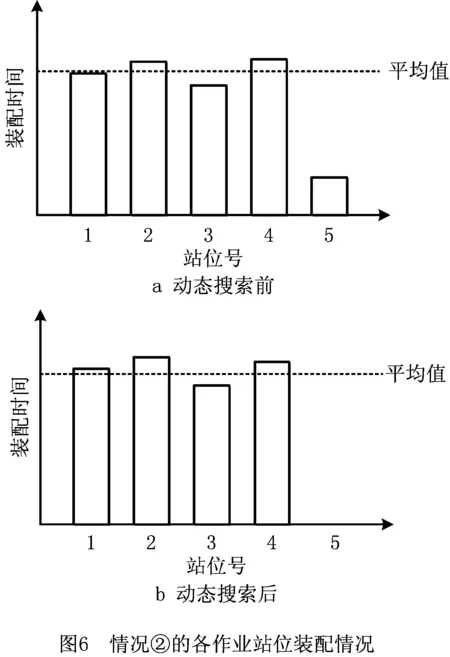
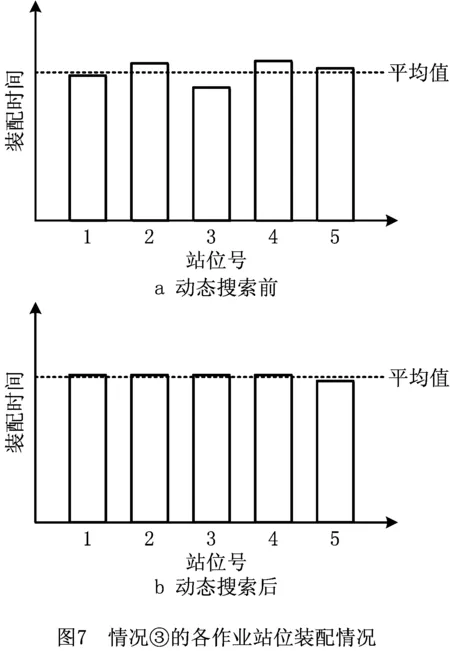
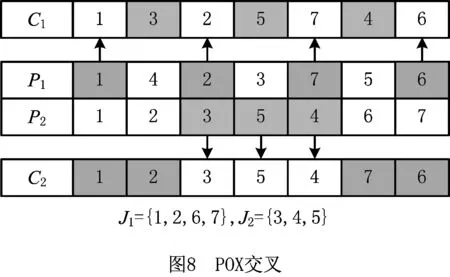
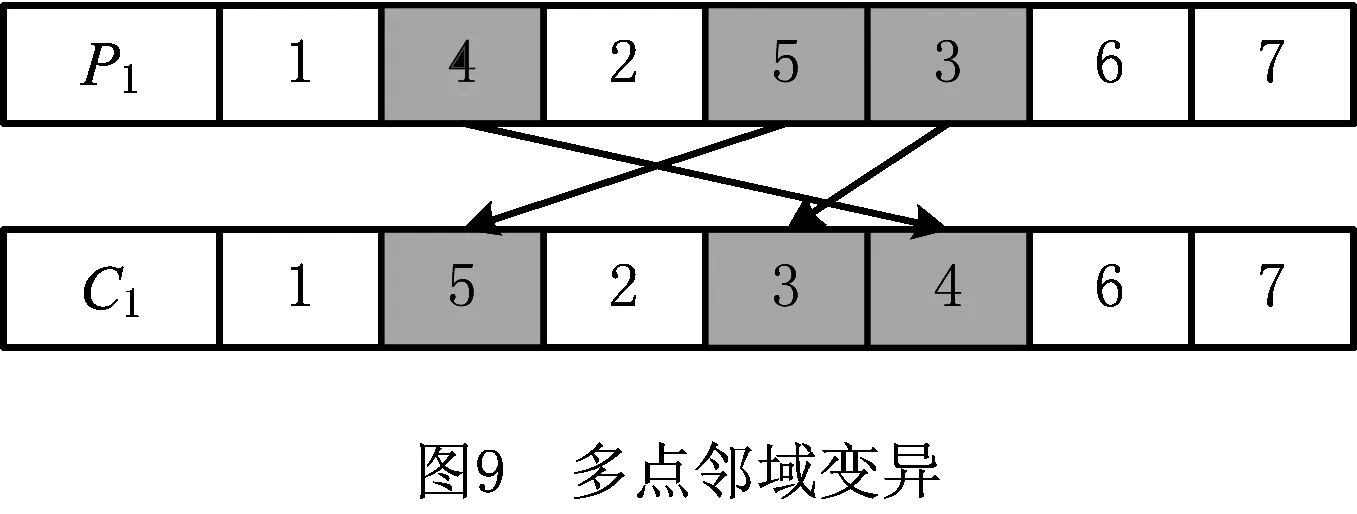
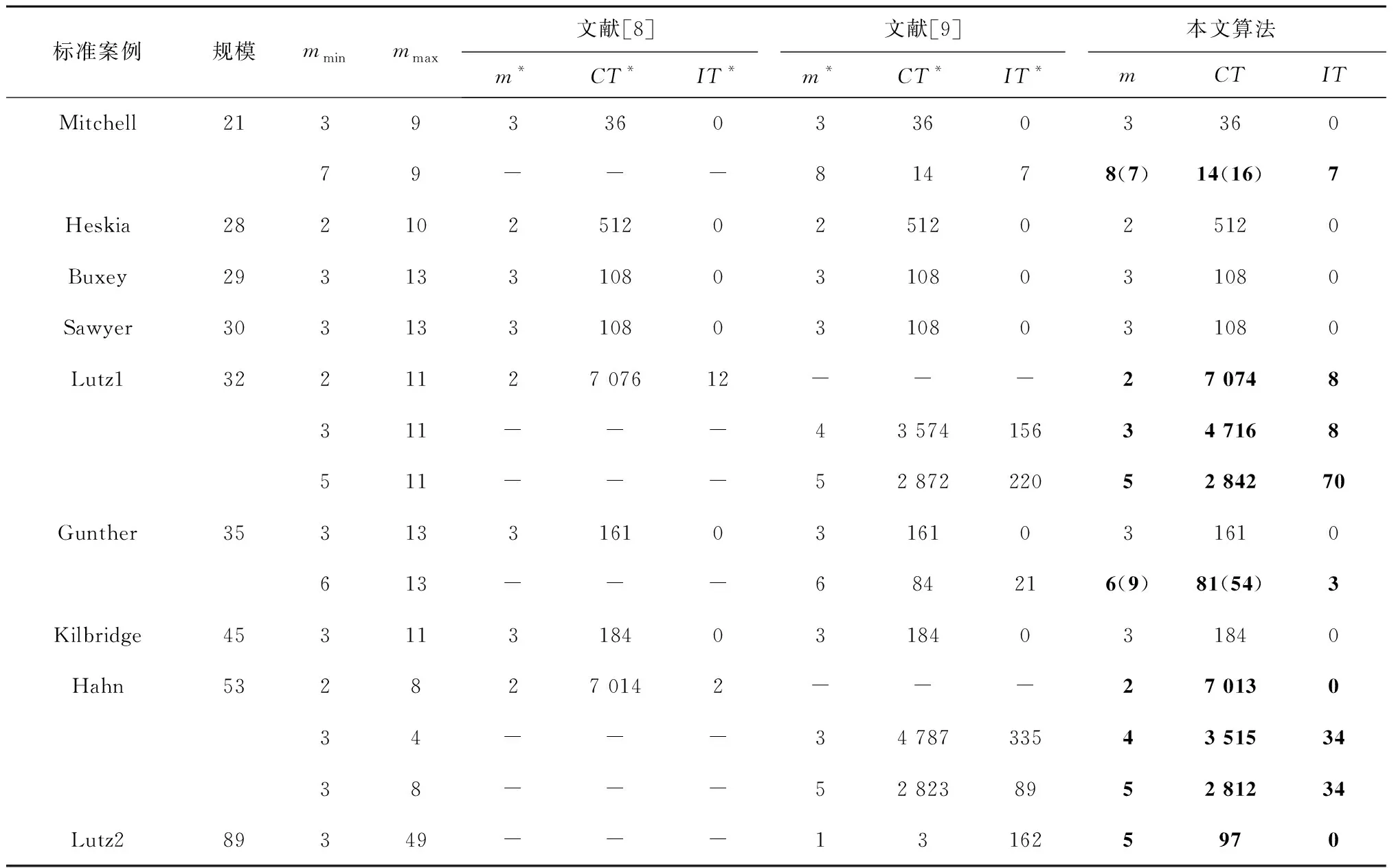
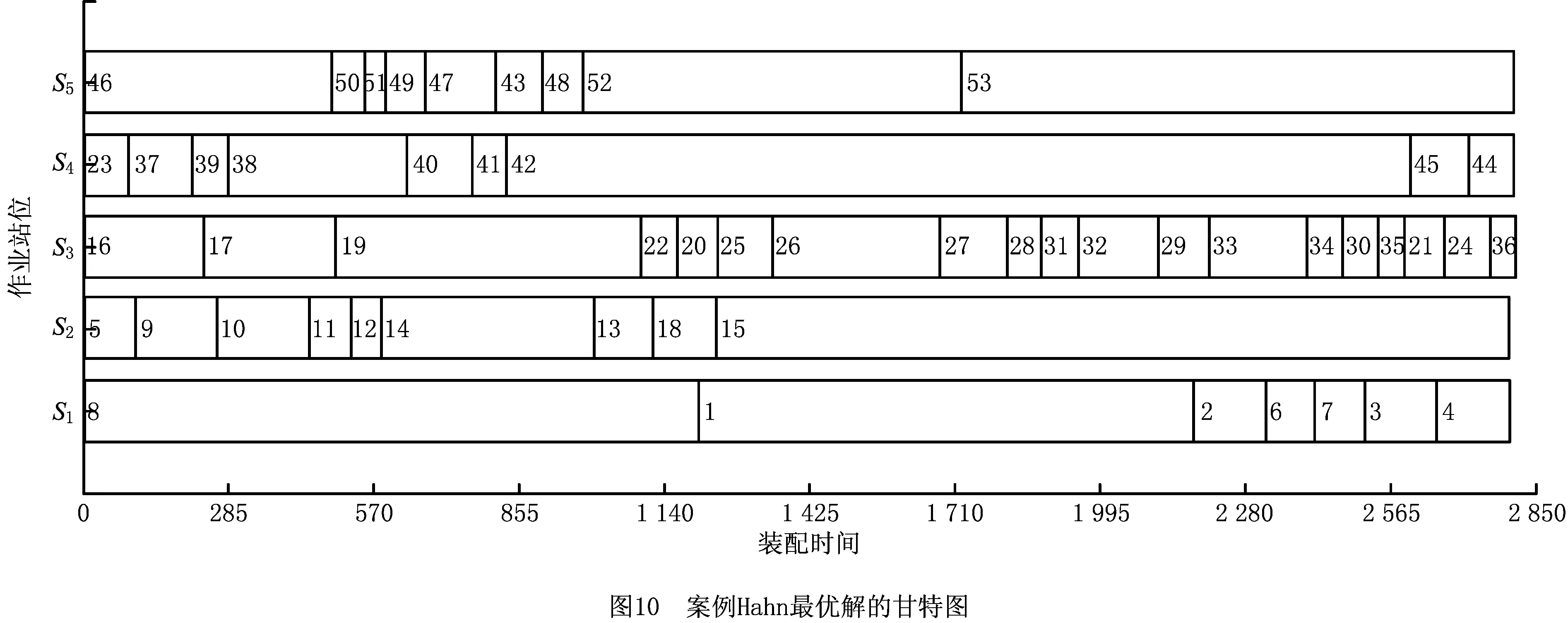
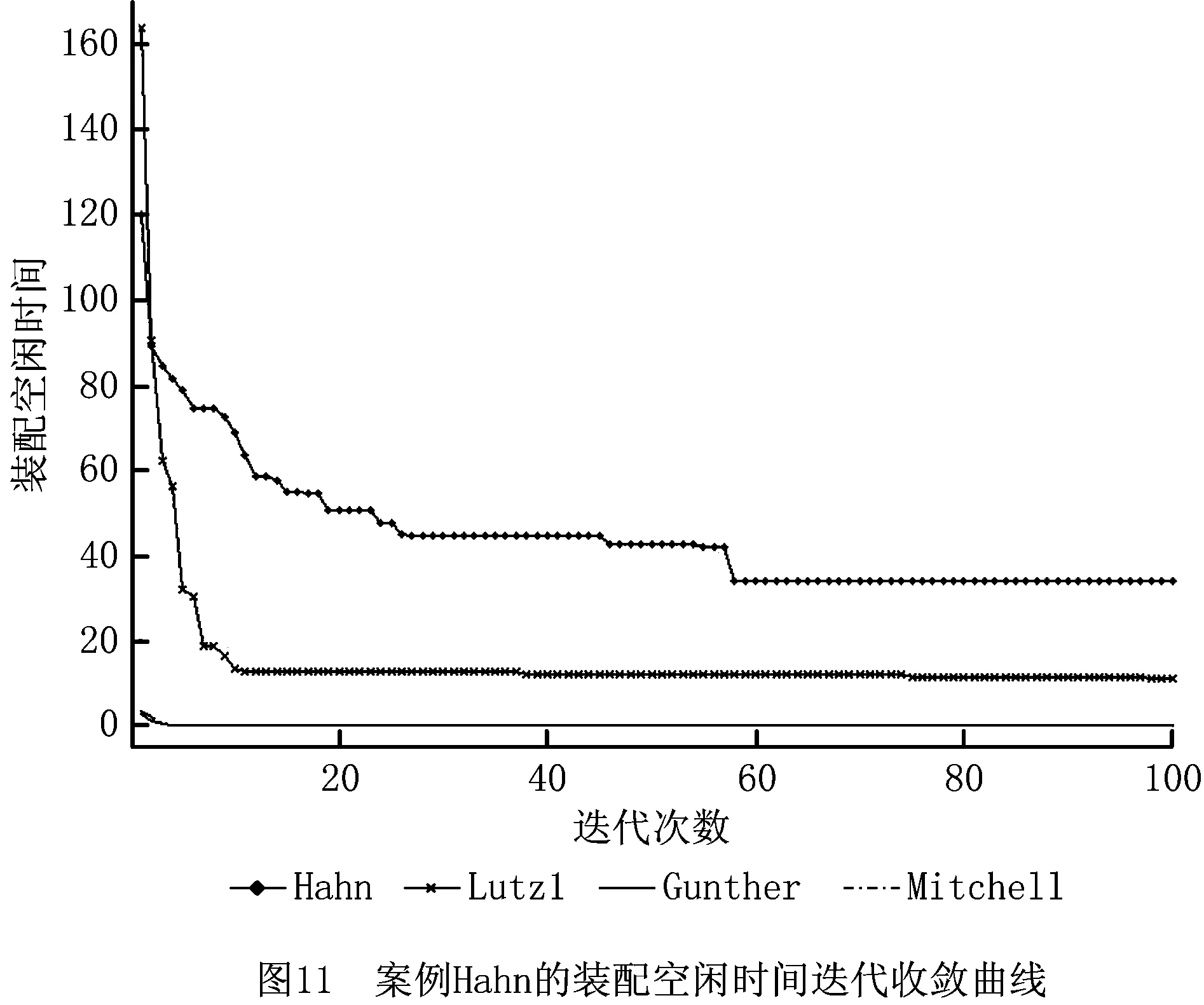
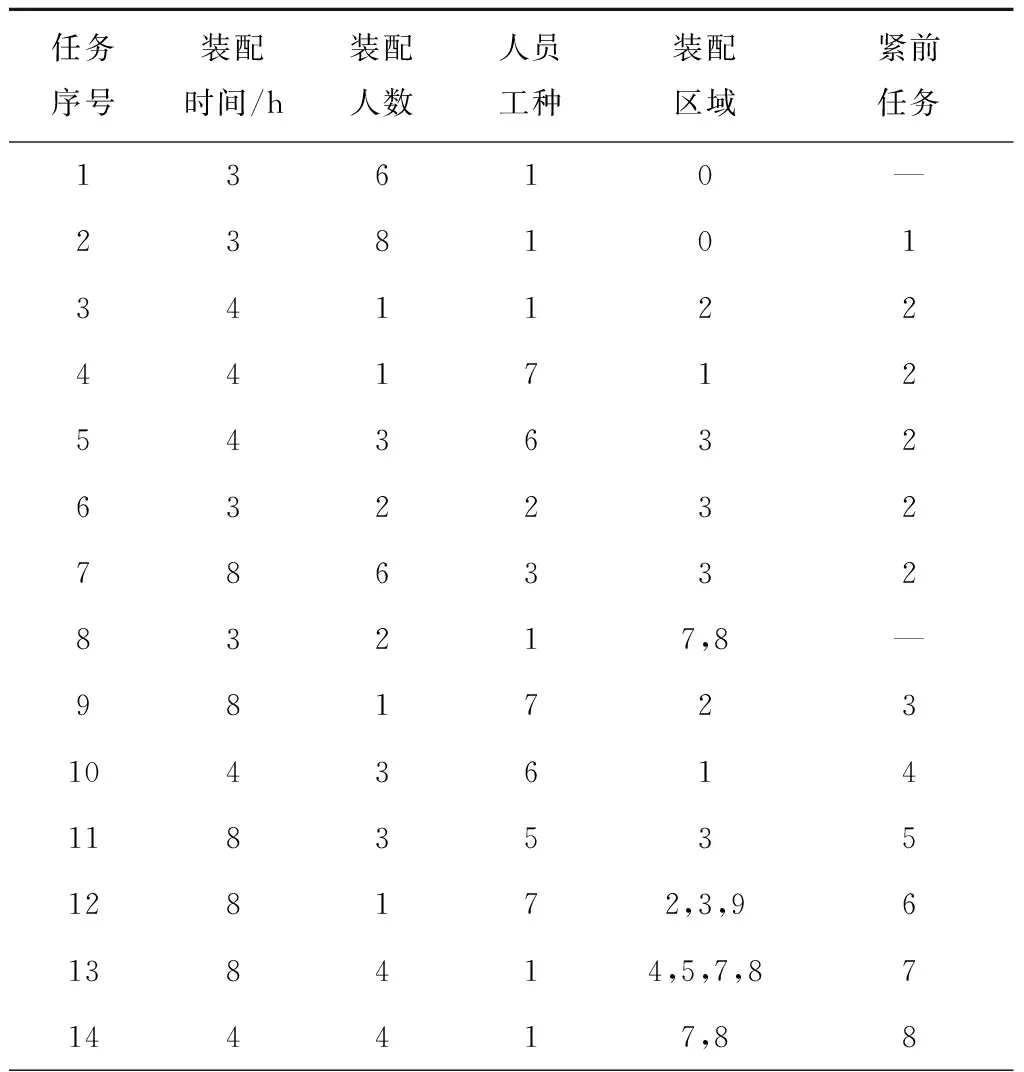
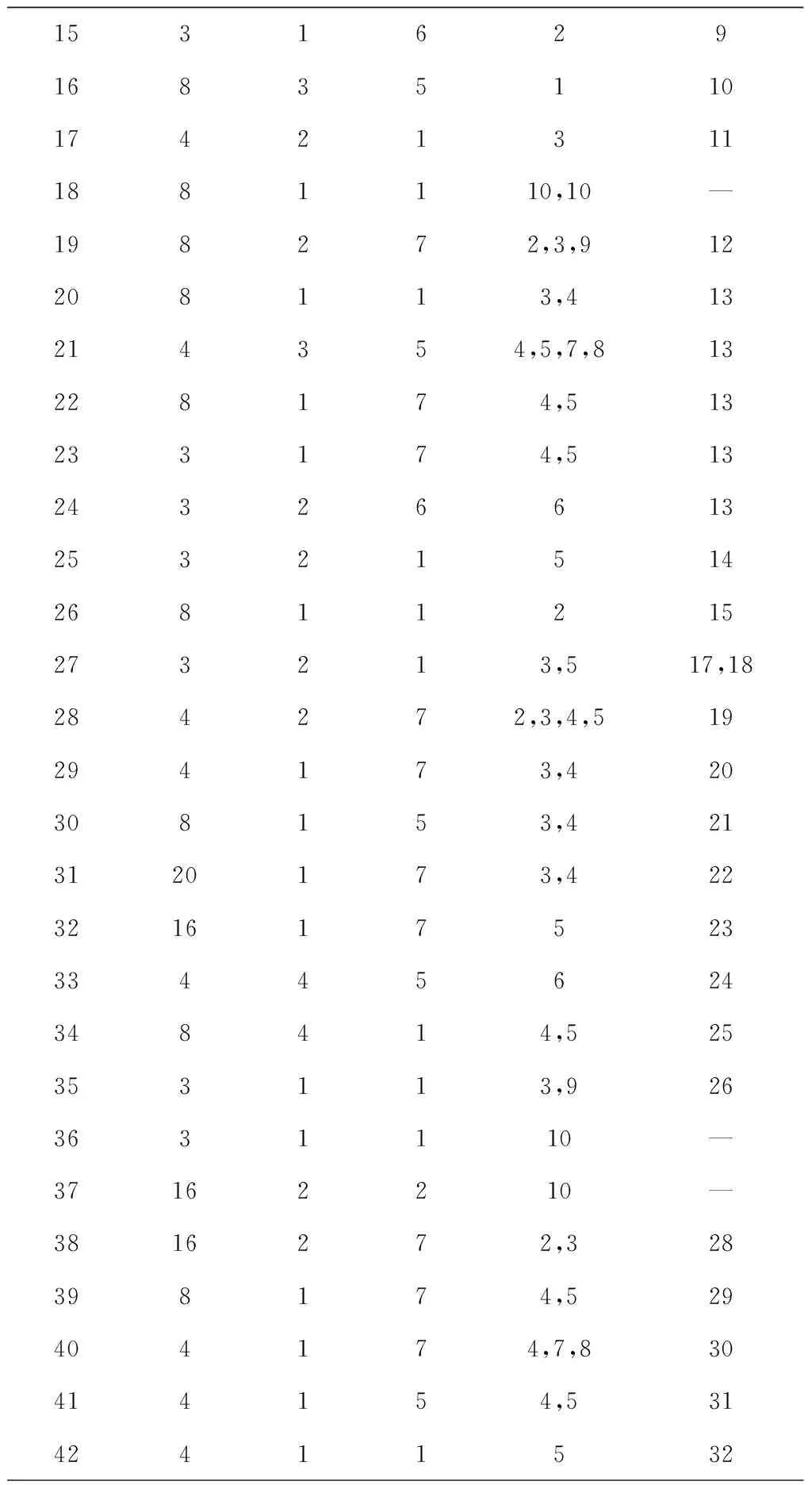
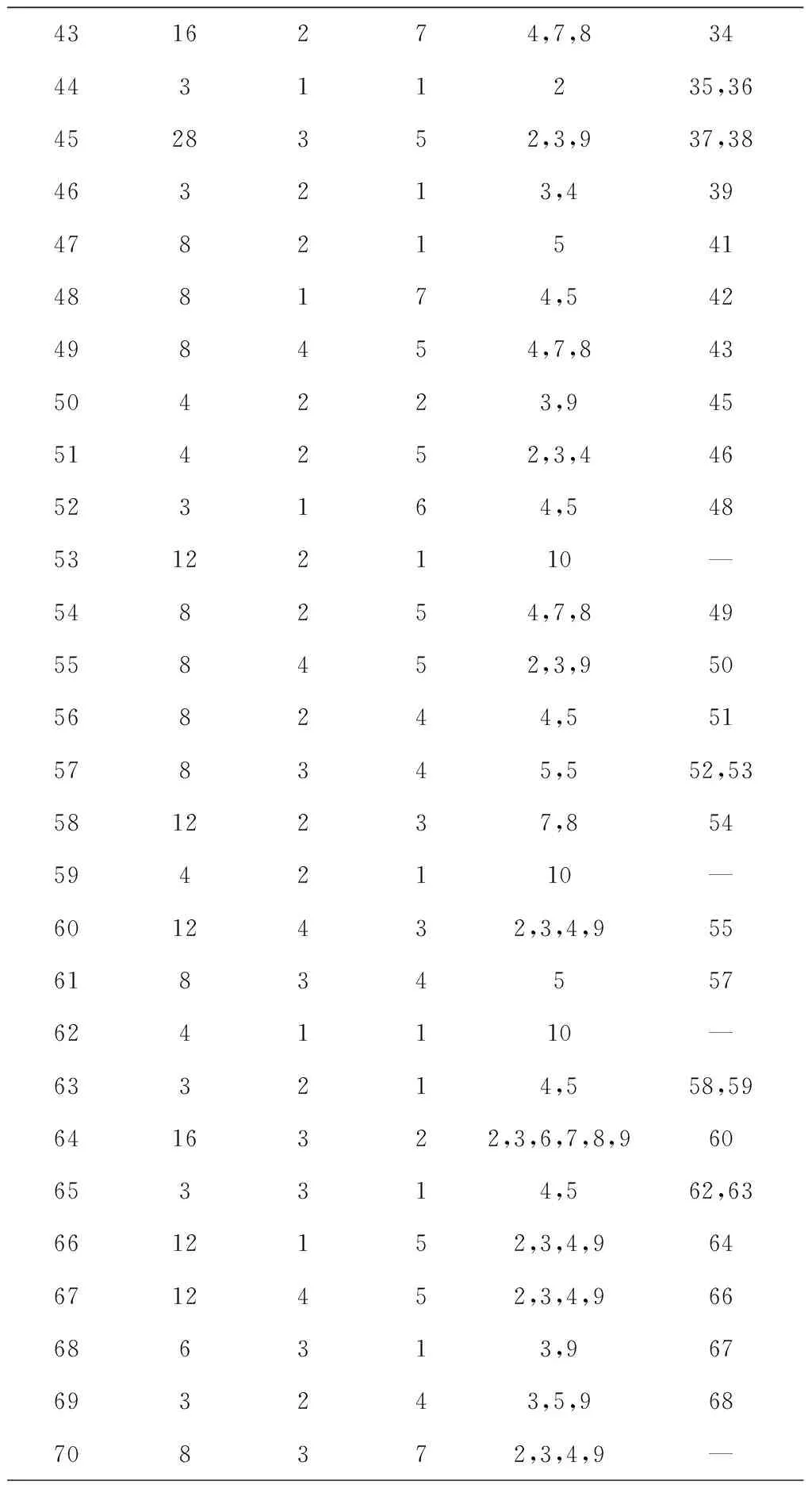
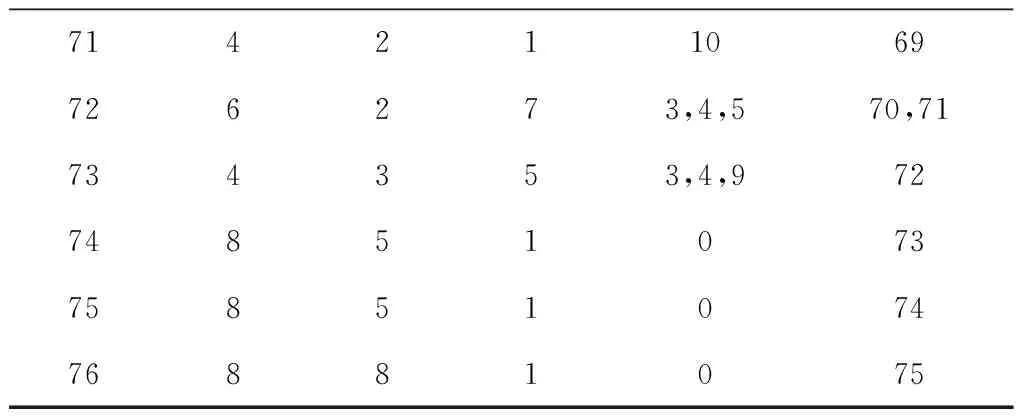
步骤3从左向右将个体编码中未被分配的前s个作业任务分配到工作站位中,并以第s作业任务为工作站位中的最后一个作业任务,使第s个作业任务满足cs≤CT 步骤4如果作业任务还有未分配的,且未分配到最后作业站位,则转步骤3,否则进行下一步操作。 步骤5当作业任务分配到最后作业站位时,将个体编码中所有未被分配的作业任务都分配到最后作业站位。 步骤6计算各作业站位的装配时间和目标函数,取当前站位装配时间的最大值作为装配节拍CT。 3.1.2 动态搜索算法 为提高解码质量和混合算法的求解效率,设计并运用动态搜索算法在多重解码过程中搜索各装配序列相应的最优站位数量和装配节拍,如图3所示。该算法根据前一次解码结果动态调整站位数量,减少对应低质量解的站位数量的解码次数,提高解码质量和求解效率,算法具体步骤如下: 步骤1对个体解码所得到的各站位装配时间和装配节拍CT进行分析,以5站位的装配线为例,可获得以下3种情况:①最后一个作业站位的装配时间远大于其余站位的装配时间平均值,如图5a所示,对二者的比值取整,其值大于1,转步骤2;②最后一个作业站位的装配时间远小于其余站位的装配时间平均值,如图6a所示,对二者的比值取整,其值小于1,转步骤3;③最后一个作业站位的装配时间接近其余站位的装配时间平均值,如图7a所示,对二者的比值取整,其值等于1,转步骤4。 步骤4如果mmin≤m≤mmax,则CT=CT+r3·tmin,其中r3为(-1,1)范围内的随机数,tmin为各作业任务装配时间最小值,对CT取整后得到的装配情况,如果结果如图7b所示,转步骤6,否则转步骤5。 步骤6根据CT和m进行解码,获取新的解并与之前解码结果进行支配关系比较,若新解支配当前的最优解或达到终止步长,则跳出结束输出本次搜索所得的非支配解及对应的CT和m,否则转步骤1。 3.1.3 布谷鸟搜索算法 CS算法由Yang等[11]于2009年提出,与其他群智能优化算法相比具有收敛速度快、算法精度高、寻优效果好等特点,本文根据站位数量寻优的特点对CS算法进行改进,在莱维飞行的随机步长计算中增加当前最优站位数量的影响因式,从而提高CS算法搜索最优站位数量的效率和质量。 (12) (13) (14) 式中:β是一个[1,2]之间的参数,此处取β=1.5;u和v服从正态分布,即 (15) (16) 在局部搜索的过程中,采用随机步长数组S更新布谷鸟蛋被发现的鸟巢,其表达为 (17) 式中r6为(0,1)的随机数。此外Pa表示布谷鸟蛋被发现的概率,这里Pa=0.25,每个鸟巢是否被发现采用数组K表示, (18) 其中随机数Ra∈[0,1]。若Ra>Pa,则鸟巢主人发现布谷鸟蛋,Ki置一;否则鸟巢主人未发现布谷鸟蛋,Ki置零,第t+1代站位数量位置 (19) 3.1.4 第二类非支配排序遗传算法 NSGA-Ⅱ由Deb[14]等于2002年对NSGA进行改进所得,其最大的改进就是采用对结果进行相似度计算遴选个体参与后续操作,从而避免种群早熟。而APALBP问题的各代结果集中度高,因此改由相同解集合中随机选取来进行个体筛选。改进后的NSGA-Ⅱ如图3所示对装配序列进行优化,具体过程如下: 步骤1由于个体的解相似度高且有大量个体对应结果相同,采取从相同结果的个体中随机选出代表个体,而不是如传统NSGA-Ⅱ采用个体之间距离衡量相似度来进行个体遴选。 步骤2对遴选后的种群进行锦标赛选择操作,个体的优劣评价采取Pareto排序,选择每次随机规模中的非支配解,组成随后参与遗传操作的新种群。 步骤3交叉操作,采用优先交叉操作(Prece dence Operation Crossover, POX)[15],交叉父代染色体中作业任务的装配顺序。操作过程如图8所示,以案例Mertens的两个装配序列染色体P1和P2的POX交叉为例,将所有作业任务随机划分为作业任务集合J1和J2,将P1中集合J1和P2中集合J2的作业任务分别复制到子代C1和C2,再将集合J1和J2的作业任务分别按P2和P1的装配顺序补充到子代C2和C1中,完成POX交叉操作。 步骤4变异操作,采用多点邻域变异。在染色体中随机选取个别作业任务,并从该作业任务集合的排序邻域中随机选取一个替代当前排序,如图9所示,从染色体P1中随机选取3个作业任务,其排序为{4,5,3},从该排序邻域中随机获取新的排序{5,3,4},并按照新的排序更新染色体获取子代C1,完成多点邻域变异操作。 O(2N)+O(N)+gen[O(m0l0N)+O(m0 (N+Ng)2)+O(m0N)+O(N)+O(PaN)+ =O(gen(m0(N+Ng)2+(m0l0+m0+ (20) 本文优化算法程序采用MATLAB 2012a编写,在Windows7 64位操作系统环境下运行,运行计算机配置为内存8 G、处理器Intel(R)Core(TM)i7-3770。优化算法参数设置如下:装配序列和站位数量种群个数Size=100,最大迭代次数gen=100,交叉概率Pc=0.8,变异概率Pm=0.8,动态搜索算法的终止步长L=mmax-mmin+1。 为测试本文算法性能,采用由文献[16]提供的SALBP-E测试案例,测试案例数据可从http://alb.mansci.de/获得,选取文献[8-9]的优化结果进行算法性能分析,对各测试案例连续运行10次,从中选取最优结果,为便于优化结果进行比较,采用相同的目标函数 (21) 式中IT为装配线空闲时间,运行结果如表1所示,其中Scale为测试案例的装配作业任务规模。各测试案例优化求解的平均运行时间均不超过20 s,由表1中优化结果对比可知本文算法在多数测试案例上的表现优于文献[8-9],且在个别案例中优化结果较历史结果减少近数倍。以测试案例Hahn为例,在站位数量范围[3,8]的条件下,本文算法所得最优解减小到仅有文献[9]历史最优解的38%,装配线空闲时间大幅减少,图10所示为案例Hahn最优解的甘特图,同时本文算法求解个别案例可获取多组优化解,证明本文算法能够有效克服目标函数的多峰特性,较文献[8-9]的算法有显著提升。 表1 测试案例优化求解结果 为检验算法的收敛性能,选取表1中的4个测试案例在各自站位数量搜索范围最大的条件下优化求解连续运行10次的所得解,对每代最优解的目标函数取平均值,获得装配空闲时间收敛曲线,如图11所示,由图可知本文算法能够在给定的有限迭代次数中获取最优解,有效避免陷入局部最优解。 为验证所建模型和求解算法的有效性,选取某飞机脉动总装生产线进行应用分析。该实例的装配任务总共有76个,作业人员根据装配工艺类别被划分为7个工种,各站位根据装配任务的作业区域被划分为11个作业区域,如图1中作业站位5所示,装配任务的数据信息和先后次序关系如表2所示。 表2 某飞机脉动总装生产线装配信息 任务序号装配时间/h装配人数人员工种装配区域紧前任务13610—23810134112244171254363263223278633283217,8—98172310436141183535128172,3,96138414,5,7,87144417,88 续表2 续表2 续表2 在与算法性能测试相同的计算机环境下,运用所提出的混合优化算法分别对案例的SALBP-E和APALBP-E模型进行平衡优化,并根据不同的装配线实施条件设置多组站位数量范围,分别对不同的站位数量范围连续运行10次,平衡优化所得结果如表3所示,其中averT为连续优化求解10次的运行时间平均值。 由表3可知,在不同的站位数量范围条件下,APALBP-E模型平衡优化所得的装配线方案在装配效率上均较SALBP-E模型平衡优化所得方案有大幅提高,并且二者优化解的人员规模相当。以站位数量范围[4,7]为例,APALBP-E模型平衡优化所得方案在装配节拍和平滑指数上均优于SALBP-E模型,在作业人员数量也较SALBP-E模型有所减少,实现了在合理的人员配置条件下提高装配效率的目标。从各最优装配线方案中选取第一作业站位作为分析对象的装配甘特图如图12和图13所示,对比发现在APALBP-E模型中在满足多约束的条件下,优化结果充分体现了飞机总装脉动生产线多工种协同装配、多区域并行作业的特点,整线装配周期大幅减小,接近实际生产情况,证明基于该模型的平衡优化结果能够有效反映飞机总装脉动生产线的实际生产。 表3 案例平衡优化的结果 本文针对飞机总装脉动生产线多工种协同装配、多区域并行作业的特点,在对SALBP-E的假设条件和约束条件进行补充细化的基础上建立多目标多约束的APALBP-E模型,并运用一种混合优化算法求解模型获取最优装配线方案,经算法性能测试和生产案例应用分析得出以下结论: (1)通过应用案例分析证明,由APALBP-E模型平衡优化所得的最优装配线方案较SALBP-E模型的优化方案在人员规模基本不变情况下的装配效率显著提升,且有效反映飞机总装脉动生产线的实际生产情况。 (2)所提出的混合优化算法在标准案例的测试中优于近年文献中的优化算法,并在个别案例中提供多组优化方案,证明该算法性能优异并能够有效解决APALBP-E的多极值问题。 综上所述,本文所建APALBP-E模型及混合优化算法可以有效解决APALBP。在后续研究中,可考虑在该模型的基础上进一步完善APALBP模型,并改进优化算法提高APALBP的结果质量和求解效率。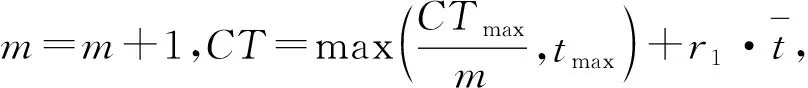
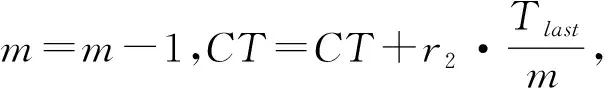
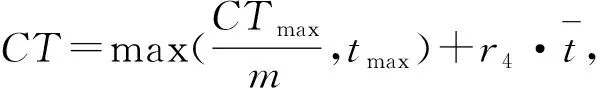
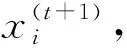
3.2 算法复杂度分析
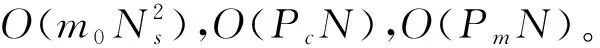
3.3 算法性能测试
4 应用实例

5 结束语