再制造拆卸服务生产线及其平衡优化

夏绪辉，周 萌，王 蕾,2+，曹建华

(1.武汉科技大学 冶金装备及控制教育部重点实验室，湖北 武汉 430081； 2.武汉科技大学 服务科学与工程研究中心，湖北 武汉 430081)

0 引言

再制造是逆向供应链的重要环节，是实现退役产品资源循环再利用和制造业节能环保的重要途径。随着世界经济从产品经济向服务经济转型，服务与传统制造、再制造逐渐融合，产生了服务型制造[1]和再制造服务[2]。再制造服务是一种综合性服务模式，包括面向客户的个性化需求服务和面向再制造加工企业的生产性服务。再制造拆卸服务(Disassembly Services for Remanufacturing, RM-DS)是再制造生产性服务中合理处理、回收退役产品零部件的前提，也是提高退役产品循环利用效益和再制造生产服务效率的关键环节，受到了国内外学者的高度关注，相关学者从再制造拆卸模型[3]、拆卸技术与工具[4]、拆卸过程规划与拆卸线平衡、拆卸系统及配置[5]等多个方面展开了研究。其中，单个退役产品的拆卸技术问题已较为成熟，但无法满足再制造批量生产的需求。RM-DS不仅要满足单产品个性化拆卸服务需求，更应能满足面向再制造生产的大批量产品拆卸需求。然而，由于再制造拆卸对象在回收数量方面的不确定性，以及在失效形式、失效程度、剩余寿命等方面的差异性，极大增加了再制造拆卸批量作业的难度，合理设计拆卸服务方案、规划拆卸服务作业流程，并提升拆卸服务生产线平衡水平，是解决问题的关键。自拆卸线平衡问题(Disassembly Line Balancing Problem, DLBP)被提出以来，相关学者针对该问题开展了系列研究，例如Gupta等[6]以最小工位数作为优化目标，提出一种基于蚁群优化算法的拆卸线平衡方法；Mcgovern等[7-8]以最小化工位数和特定的零部件为目标，提出一种基于贪婪算法的拆卸线平衡优化方法；丁力平等[9]针对DLBP，提出以负载均衡和最小化拆卸成本为目标的改进型Pareto解集的蚁群优化算法；朱兴涛等[10]在考虑有限拆卸危害和特定零部件的基础上，提出一种基于混合搜索机制的蚁群算法；Altekin等[11-12]提出以技术和经济可行性为目标的再制造产品拆卸线平衡优化方法；李明等[13]提出以负载均衡和最小拆卸序列为目标，基于改进型人工蜂群算法拆卸线平衡优化方法。上述研究大多是对遗传、蚁群、蜂群等智能算法进行改进来求解经典的拆卸线平衡多目标优化问题，较少涉及再制造拆卸及其服务的内涵、模式等问题，而且在计算方面，蚁群、蜂群等智能算法参数选择及计算过程较为繁杂。本文根据再制造服务的理念，提出再制造拆卸服务的概念以及生产线服务模式，并构建以拆卸生产线最大化负载率均衡和优先拆卸高价值的零部件为目标的再制造拆卸服务生产线平衡优化模型，在无复杂参数设置的新型智能算法——教与学优化(Teaching-Learning-Based Optimization, TLBO)算法[14-16]的基础上，提出一种基于改进型TLBO(Improved TLBO, ITLBO)的再制造服务拆卸线平衡优化算法，借助经典实验对比验证算法的有效性，通过工程实例验证模型和算法的实用性，为再制造拆卸服务的研究提供了思路与方法。

1 再制造拆卸服务生产线

1.1 再制造拆卸服务

再制造服务是以再制造服务集成商(平台)为核心，以再制造企业群为主体，以再制造服务化为基础的一种将整合资源分散服务和提升再制造价值的个性化集成服务方式[2]。再制造服务主要包括两方面：①直接面向客户需求的再制造价值增值服务活动，如再制造性评估服务、再制造设计服务、再制造工程整体解决方案服务等；②面向再制造企业的生产性专业服务，如再制造回收服务、再制造拆卸服务、再制造加工服务等。

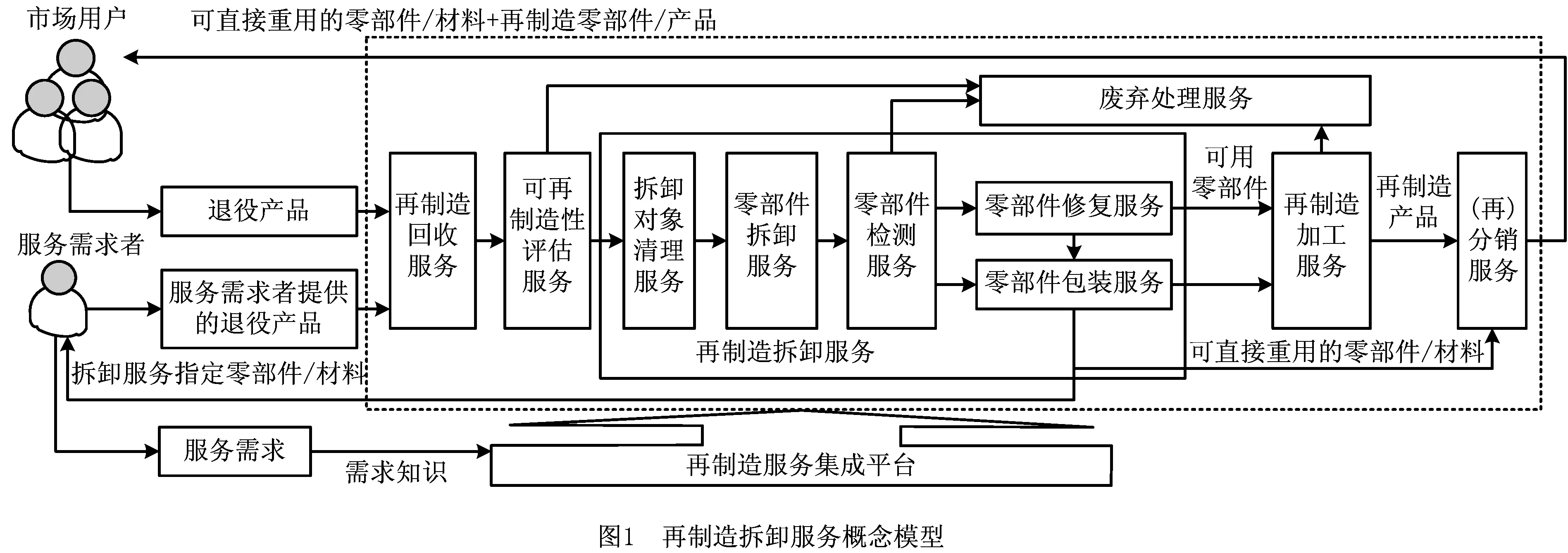
RM-DS作为再制造服务的重要组成部分，是废旧产品再制造资源最大化利用的重要前提，是实现产品多生命周期的必要环节。作为面向再制造生产服务的新型服务体，RM-DS可理解为：以再制造服务集成商/集成平台为核心，由拆卸服务企业或者制造/再制造企业中的拆卸部门构成的拆卸服务企业群面向客户或再制造生产企业的专业服务，其以拆卸专业化和服务化为基础，根据服务需求及服务对象特点，提供专业的拆卸服务方案、系统的拆卸加工，以及从服务对象中获取的指定材料或零部件，其概念模型如图1所示。

RM-DS的主要功能包括：①以提升废旧产品价值为目的的面向客户需求的个性化拆卸服务，包括向客户提供复杂设备拆卸方案、为客户拆卸其提供的指定废旧产品并返回有价值的零部件,以及按客户需求面向市场回收废旧产品并向客户返回指定零部件；②以满足再制造生产需求为目的的面向再制造企业群的批量拆卸服务，即根据再制造服务集成平台给定的服务任务，分类拆卸从市场回收的大量废旧产品，并向不同的再制造加工企业批量提供不同的废旧零部件。

1.2 拆卸服务生产线

目前,国内废旧产品拆卸主要是作坊式人工拆解，这种方式数量多、规模小，拆卸技术落后，再生利用率低。根据再制造拆卸服务的功能要求，为了提高拆卸服务效率、推动拆卸服务专业化和产业化，构建具有高柔性的再制造拆卸服务生产线是实现面向再制造企业群的批量拆卸服务的前提和重要保障。拆卸服务生产线是根据逆装配法解除产品零部件间的约束联接，并将其逐个分离，由一定的设备、工具和手段构成的流水线。考虑到拆卸的经济性，具有可重复利用价值的部件在部件级即进入再制造或维修，获得单一材料的各拆卸部分可在材料级进入循环利用。拆卸服务生产线上的拆卸过程由一系列拆卸任务构成，每个拆卸任务均有对应的拆卸时间，其中部分拆卸任务之间存在拆卸顺序上的先后约束。根据再制造拆卸服务企业(部门)的规模、功能定位和服务需求，采用不同的拆卸生产线方案。

(1)单产品拆卸服务生产线 主要包括单台单产品个性化拆卸和多台单产品批量拆卸。前者主要针对客户个性拆卸需求展开，拆卸场地等可能不固定，通常无需生产线；后者主要针对批量拆卸，其拆卸服务生产线主要包括单产品直线型拆卸生产线和单产品U型拆卸生产线两种。

1)单产品直线型拆卸生产线 直线型拆卸生产线适用范围广、布局简单。例如某再制造产品共有n个拆卸操作，可根据节拍划定其工位。根据零件拆卸任务优先约束关系确定的布局如图2所示。

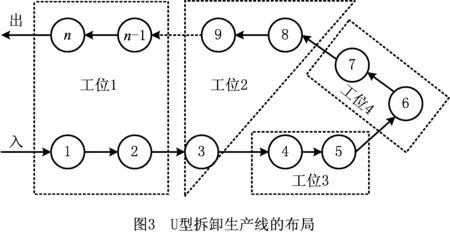
2)单产品U型拆卸生产线 相对于直线型拆卸生产线，U型拆卸生产线布局紧凑、物流成本低、拆卸线效率高。其布局是在零件优先约束关系的条件下，考虑入口和出口的位置同一性、操作人员的右手作业惯性等[13，17]，以U型逆时针流动布局的拆卸生产线如图3所示。构建U型拆卸生产线时需考虑产品特性，对于同一种产品，U型拆卸生产线的工位数目远少于直线型。

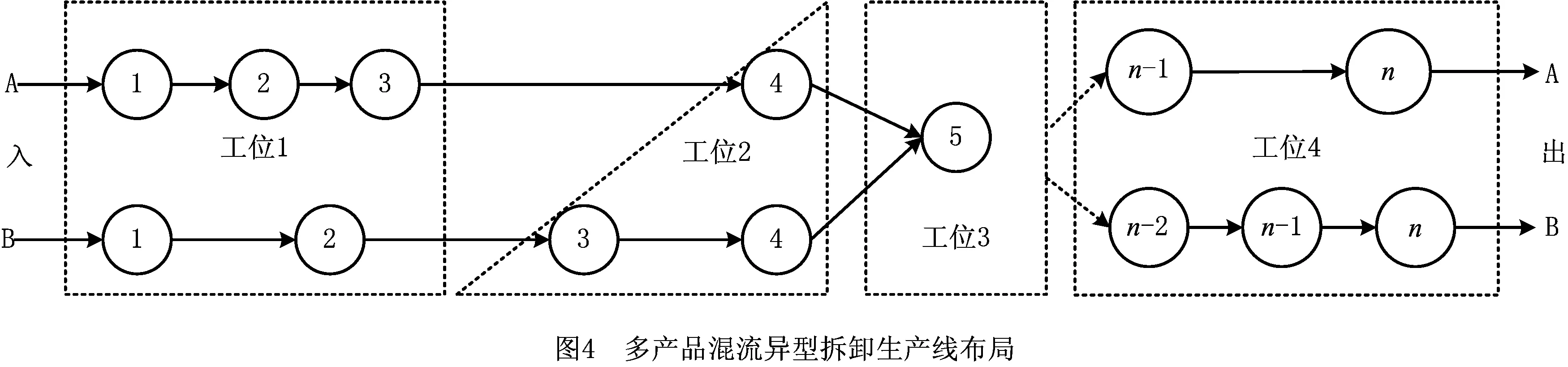
(2)多产品混流拆卸服务生产线 根据拆卸优先约束关系和生产线节拍划定工位，各工位可以完成不同产品的不同拆卸操作。批量再制造拆卸服务应尽可能考虑具有较大结构相似度的多产品，构成混流拆卸生产线。图4所示为A，B两种同类不同型号的混流拆卸生产线布局。相对于单产品拆卸服务生产线，多产品混流拆卸服务生产线可优化资源配置，降低企业生产成本。

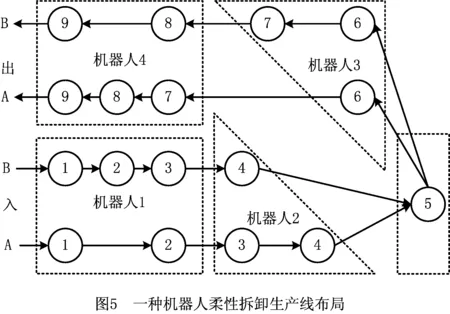
(3)基于机器人的柔性拆卸服务生产线 在拆卸服务生产线上，工业机器人能代替人做一些单调、频繁和重复的长时间作业，因此可借鉴柔性制造系统(Flexible Manufacturing System, FMS)的思想，构建基于机器人的拆卸服务生产线。该生产线不仅能对单台复杂设备进行拆卸，而且能对单品种以及多品种产品进行批量拆卸。该拆卸生产线以U型和混流异型为主，各工位可设一台或多台工业机器人。图5所示为A,B两种不同类型产品的机器人拆卸生产线布局。

虽然以上3种拆卸服务生产线的布局形式不同，但是无论哪种生产线均会涉及平衡问题。同时，因退役产品失效形式、失效程度的差异性，例如产品在使用过程中因杂质、污垢，或因漆层变质、润滑及燃油系统残留污垢、金属表面产生的腐蚀物等，导致退役产品的质量和特性具有不确定性，从而增加了退役产品拆卸难度，加大了拆卸服务生产线计划、调度难度和运行成本。为了提高再制造拆卸服务生产线的整体效率，在合理地设计拆卸服务方案、规划拆卸服务作业流程的基础上，提升拆卸服务生产线平衡水平，是解决问题的关键。规模化RM-DS的研究及应用还处于起步阶段，单产品拆卸服务模式中的单产品直线型拆卸生产线是当前典型的拆卸服务模式，其平衡问题具有较好的代表性，故本文针对RM-DS中单产品直线型拆卸服务生产线的平衡问题开展进一步的优化研究。

2 再制造拆卸服务生产线平衡优化模型

2.1 数学描述

单品种直线型拆卸服务生产线平衡问题的目标为：在规定计划期内，根据拆卸对象的拆卸工艺方案确定拆卸任务优先关系约束，据此确定拆卸工位的分配任务、操作节拍等，使得拆卸生产线最大化负载均衡率。此外，为了提高再制造的价值，需要优先拆卸废旧产品中高价值零部件。

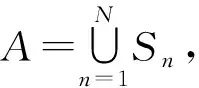
2.2 模型假设

在进行RM-DS生产线平衡问题的建模过程中，为了避免模型过于复杂，进行如下假设：

(1)再制造产品是完全拆卸的。

(2)再制造产品拆卸任务的拆卸时间是唯一确定的，非随机性变化。

(3)拆卸任务是不可分的最小自然单位，一个拆卸任务仅能在一个工位上完成，且每个拆卸任务之间相互独立。

(4)拆卸生产线的节拍大于拆卸任务时间中的最大者。

(5)再制造产品零件除了拆卸的优先约束关系以外，没有其他的约束限制。

2.3 模型构建

RM-DS生产线平衡优化主要考虑以下两个目标：

(1)均衡各工位负载 为保证再制造服务拆卸生产线高效运行，尽量降低再制造产品在线阻塞，为了能在兼顾最小工位数的同时又确保生产线的负载均衡[10]，需要使各工位的操作人员具有相对均衡的作业负荷，该目标表示为

(1)

(2)优先拆卸高价值零件 RM-DS生产线中，越早拆卸有价值、高价值或者高需求的零件，越快给企业带来经济效益，为保证拆卸服务生产线的零件效益最大，优先拆卸高需求的零部件，目标表示为

(2)

根据以上分析建立再制造拆卸服务生产线平衡模型如下：

minZ=(Z1,Z2)。

(3)

s.t.

j=2,3,…,M,j>1;

(4)

其中：CT为RM-DS生产线的节拍;n为工位序号;F为均衡指数;N为工位数量;M为拆卸任务的总数目;m为第m个拆卸任务;tm为第m个拆卸任务的拆卸时间;xmn是一个0-1的变量，表示若第m个任务分配到第n个工位，则xmn=1，否则xmn=0;Sn为分配到工位n的拆卸任务;Qn为Sn中拆卸任务的数目。式(4)中约束1保证任意一个拆卸任务m的不可分割性，只能被分配到一个工位中，约束2表示拆卸任务集中的所有拆卸任务都要被分配，约束3表示工位n中的拆卸任务数目，约束4保证每个工位的拆卸任务作业时间不能超过拆卸生产线的节拍，约束5保证拆卸任务之间的优先约束关系不能违反，约束6表示工位数目N的取值范围。

3 改进教与学优化算法

3.1 改进型TLBO算法

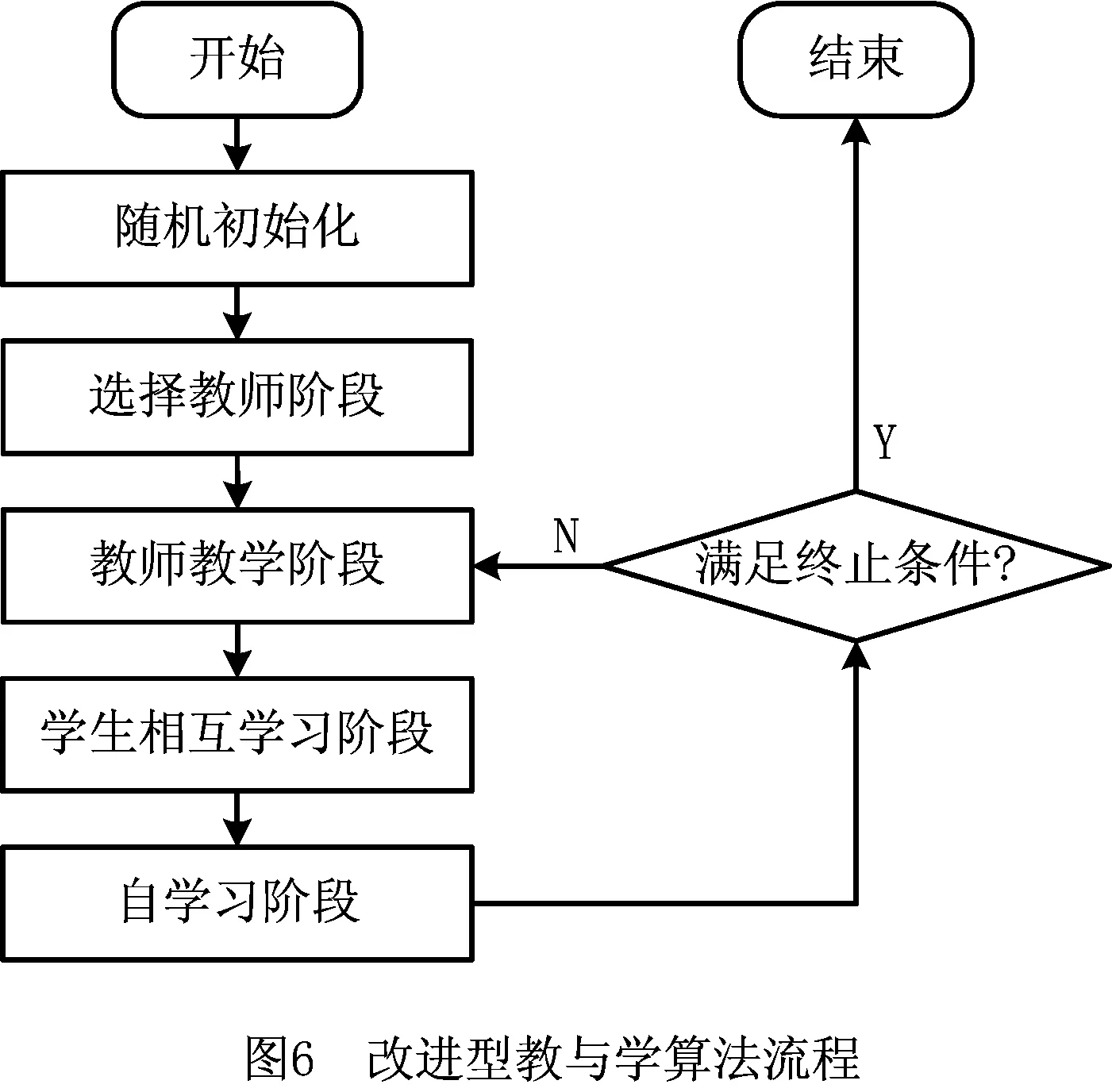
TLBO算法是Rao等[18]提出的一种新的进化算法。传统的TLBO算法模拟了老师传授及学生获取知识的过程，提出个体向更优个体学习，从而提高自身水平和能力的进化思想。该算法主要分为“教学”和“学习”两个阶段，相对于其他智能算法，具有参数少、计算效率高、收敛速度快、求解精度高的特点。但是，在学生的实际学习行为中，“学生”在向更优个体学习的同时，其本身也具备优化发展的潜质，若“学生”因学习他人而丧失自身优势，则将降低其自身价值，即“学生”应在吸收他人之长补自身之短的同时，发扬自身优势。基于该思想，本文在传统TLBO的“教学”和“学习”阶段之后，增加“选择教师”阶段，根据学生水平进行分组教学，然后进入“自学习”阶段，拟通过个体互学习和自学习达到充分优化学习的目的。改进型TLBO算法流程如图6所示。其中，考虑“学生”在对多类知识进行学习时易出现“偏科”，在“自学习”阶段重点根据“学生”特点，对其成绩较弱的知识进行加强性学习。

算法具体步骤如下：

步骤1随机键初始化。TLBO算法通常用于求解连续优化问题，考虑拆卸线平衡本质为离散优化问题，在求解前采用随机键方法[19]进行初始化，通过优先级的编码方式使每个操作分配相应的优先权值，优先权值大的先分配。本文以文献[20]中10个任务的实例解释初始化过程，对应10个任务的每个位置上产生一个随机数，以随机数的大小决定任务的拆卸顺序，随机键初始化如表1所示。设定随机数大的任务优先拆卸，则对应随机数大的操作应该排在操作序列的前面。例如，操作3对应的随机数0.94最大，其排在操作排序的第1位；操作9对应的随机数为0.91，它排在操作排序的第9位。

表1 随机键初始化

步骤2选择教师阶段。为了克服单个老师的教学缺陷，允许教师的个数超过1个。将学生按水平高低分组，按各组水平层次配备不同水平教师教学，当某低级别学生小组达到教师水平时，给该组重新分配更好的教师进行教学。具体的教学方式如下：

f(xteacher1)≥f(xi)≥f(xteacher2);

(5)

f(xteacher2)≥f(xi)≥f(xteacher3)。

(6)

式中Xteacher1表示种群中适应值最好的个体，将Xteacher1作为首席教师，以首席教师为基础，选取其他教师，根据适应值给各个教师分配小组。式(5)中，将teacher1分配xi组。

步骤3教学阶段。该阶段每位学生基于Xteacher与其平均值Xmean间的差异性展开学习。该阶段中有学习步长ri和学习因子TFi2个重要参数。其中ri为0～1之间的随机数，TFi随机取值1或2。具体的教学方式为

Xnew=Xi+ri×(Xteacher-TFi×Xmean)。

(7)

式中：Xi和Xnew分别表示学生学习前和学习后的值，Xteacher表示老师的值，Xmean是所有学生的平均值。

步骤4互学习阶段。在相互学习期间，每一位学生Xi都会随机从班级中抽取一个学习目标Xj(j≠i)，通过比较自身与Xj的差距不断调整自身，改进的方法同差分算法中的差分变异算子相似，差异在于教与学算法的学习步长对不同学生赋予不同的学习因子。学生相互学习的过程如下：

当f(Xj)>f(Xi)时，有

Xnew=Xi+ri×(Xj-Xi);

(8)

当f(Xi)>f(Xj)时，有

Xnew=Xi+ri×(Xi-Xj)。

(9)

式中f(Xi),f(Xj)分别表示学生Xi,Xj的目标函数值。在学习期间，学生间的相互交流可使其取长补短。每位学生的学习发生在小范围学员间，不会太早聚集于全局最优解方向，因此可以保持学生的多样性特征，确保算法的全局探索能力。

步骤5自学习阶段。在TLBO算法中，教学阶段实现了全局搜索，互学习阶段实现了局部搜索。由于拆卸线平衡问题约束较多，为了增强局部搜索能力，在学习阶段后增加自学习阶段，使得在跳出互学习阶段的局部最优后，能进一步优化全局最优解。

由于每个学员可能同时学习多门课程(多个决策变量)，在进行自学习时只是对部分科目进行调整学习，保持优势学科，增强劣势科目。自学习阶段伪代码如图7所示。

3.2 算法验证

为了验证改进型教与学优化算法在解决RM-DS生产线平衡问题上的有效性，本文对2个经典实例进行求解验证。实例1为文献[21]中10个拆卸任务的实际案例，实例2为文献[9]中的52个拆卸任务的实际案例。算法编程语言采用Microsoft Visual C++语言进行编程，并在配置为2.50 GHz Intel(R)Core(TM)4 GB内存的个人计算机上运行。利用层次分析法、加权、归一化等数学方法处理后构建复合目标函数

i=1,2,3,…。

(10)

式中：Z1i和Z2i分别是第i个解时两个目标函数的值;Z1max和Z2max分别是Z1和Z2的最大值，Z1min和Z2min分别是Z1和Z2的最小值;w1和w2为权重系数，一般取w1+w2=1，w1和w2的取值根据目标函数对拆卸服务生产线负载平衡和对零部件的需求指数确定。每个案例运行10次，记录平均值。算法的终止条件为运行时间达到nt×nt×10 ms。

实例1和实例2的优先约束关系分别如图8和图9所示，圆圈中的数字表示产品零件拆卸任务编号，括号里的数字表示每个拆卸任务对应的拆卸时间，箭头表示拆卸任务的优先关系。

将本文提出的改进型TLBO算法与遗传算法(Genetic Algorithm, GA)的结果进行对比，表2所示为实例的对比结果。

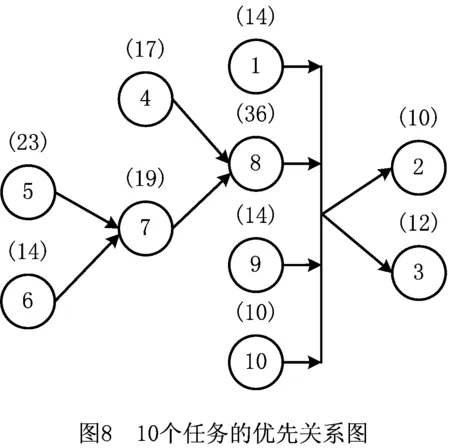
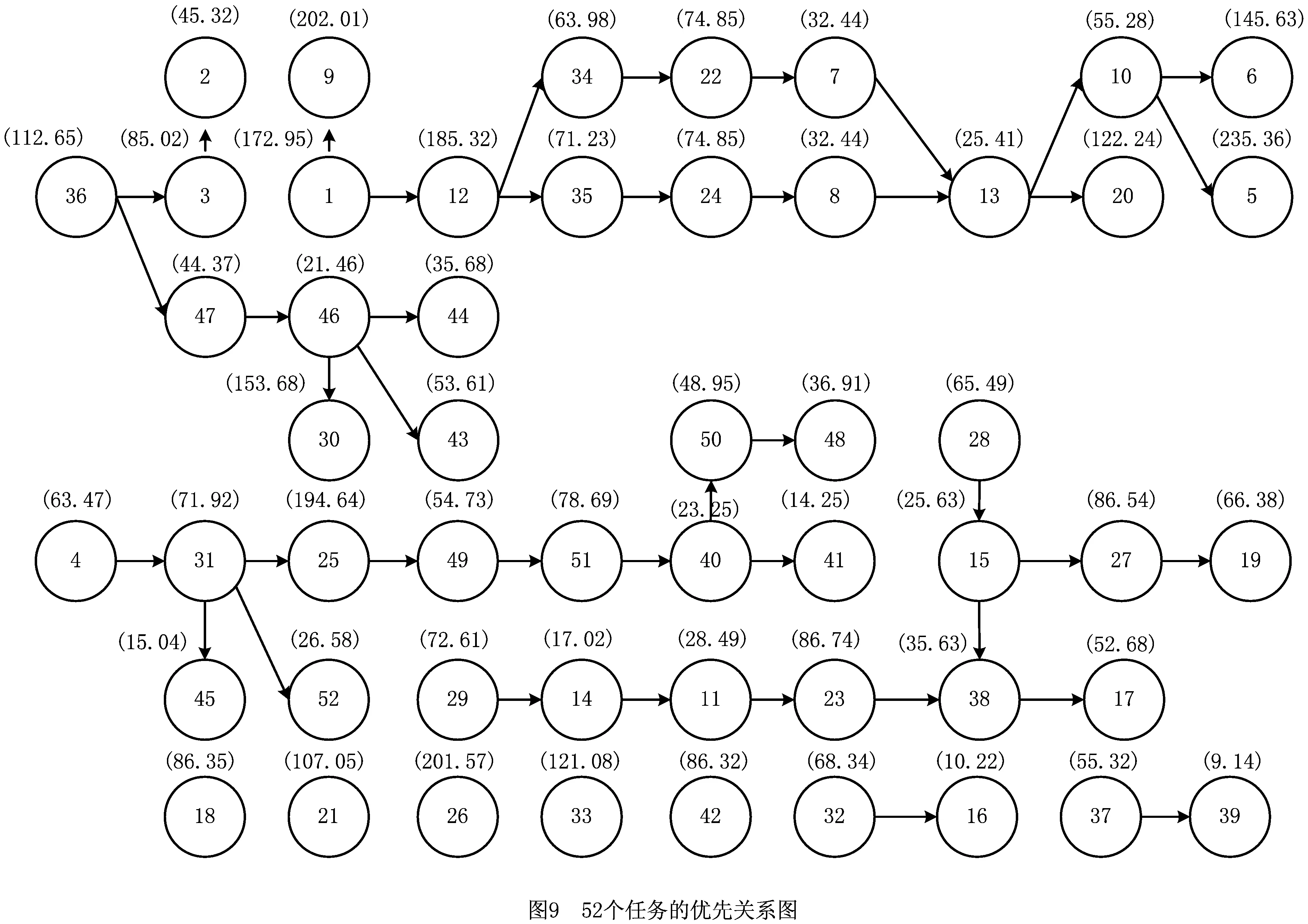
表2 算法求解结果对比

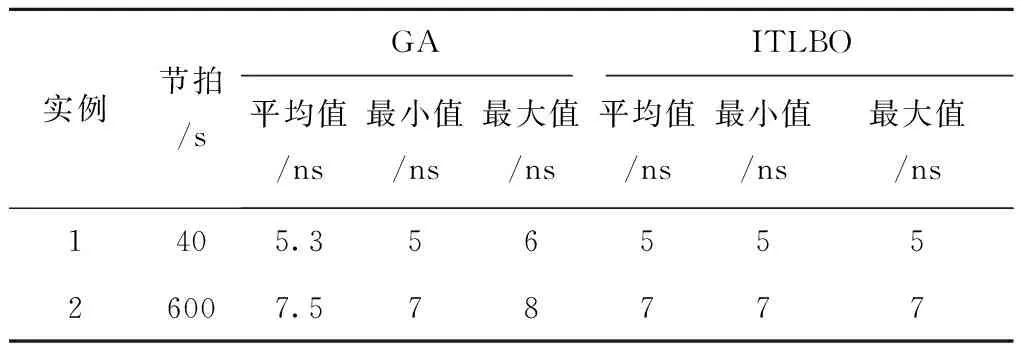
实例节拍/sGAITLBO平均值/ns最小值/ns最大值/ns平均值/ns最小值/ns最大值/ns1405.35655526007.578777

由表2可知，对于实例1和实例2，改进型TLBO算法所得到的解均优于GA，有效说明了所提改进型TLBO算法的优越性。GA和改进型TLBO算法求解实例1和实例2得到的最优拆卸方案分别如表3和表4所示。

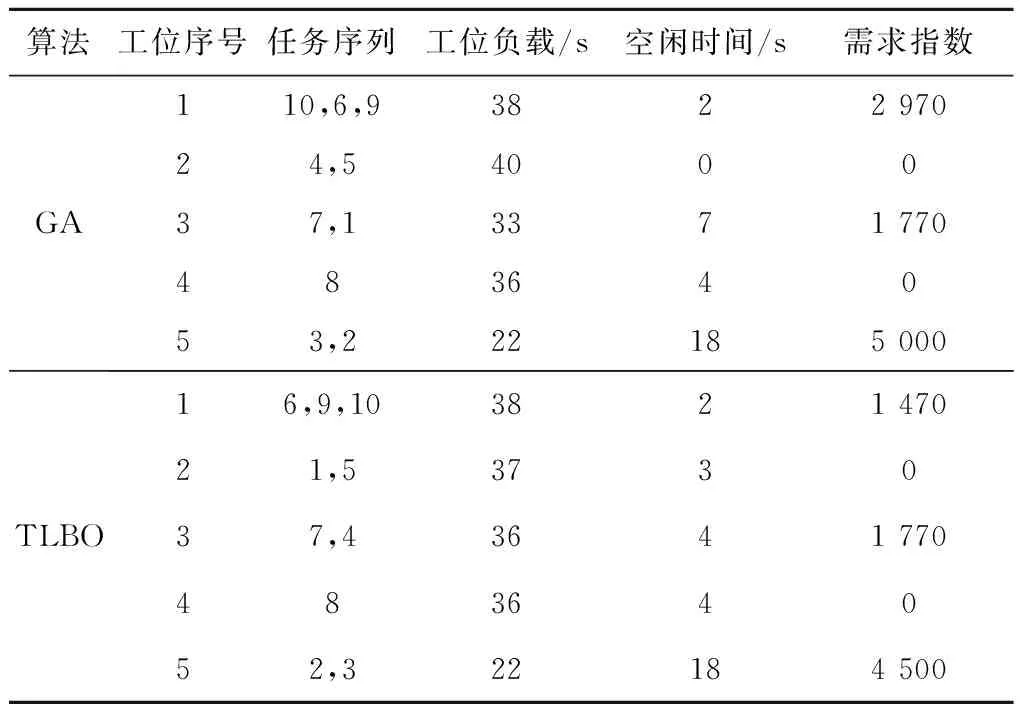
表3 10个任务实例GA和TLBO求解的最优拆卸方案

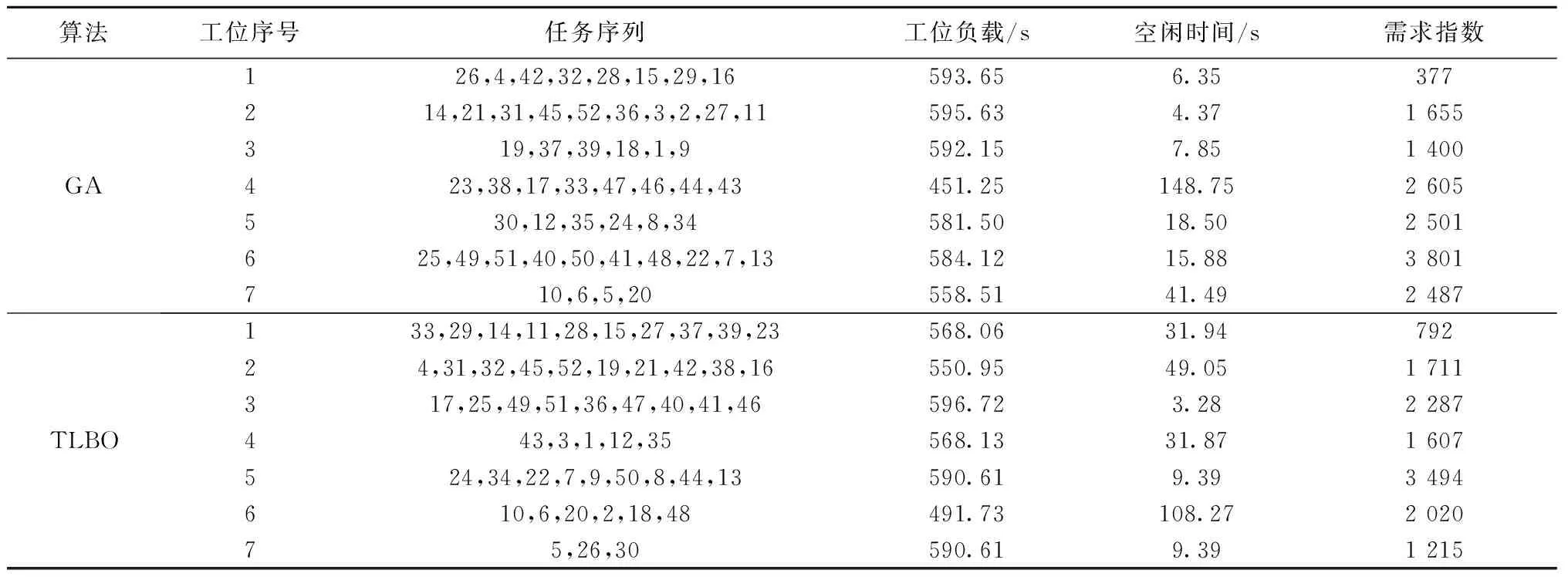
表4 52个任务实例GA和TLBO求解的最优拆卸方案

由表3可知，对于实例1，采用GA得到的工位数为5个，工位负载最大值为40 s，最小值为22 s，之间相差18 s，相对于给定节拍时间40 s，时差比例为45%，零部件需求指数之和为9 350；而采用改进型TLBO算法得到的工位数为5个，工位负载最大值为38 s，最小值为22 s，之间相差仅16 s，相对于给定节拍时间40 s，时差比例仅为40%，零部件需求指数之和仅为7 740。由表4可知，对于实例2采用GA得到的工位数为7个，工位负载最大值为595.63 s，最小值为451.25 s，之间相差144.38 s，相对于给定节拍时间600 s，时差比例为24.06%，零部件需求指数之和为14 826；而改进型TLBO算法得到的工位数为7个，工位负载最大值为596.72 s，最小值为491.73 s，之间相差仅104.99 s，相对于给定节拍时间600 s，时差比例仅为17.50%，需求指数之和仅为13 126。由上述结果对比分析可知，所提出的改进型TLBO算法在解决DLBP上明显优于GA，且求解效率比较高。

4 案例分析

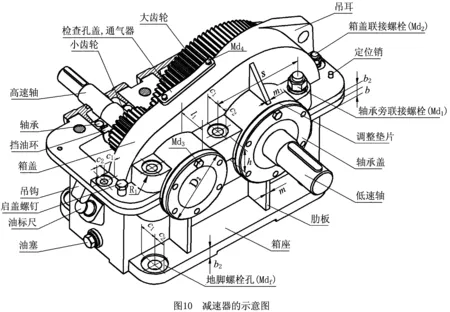
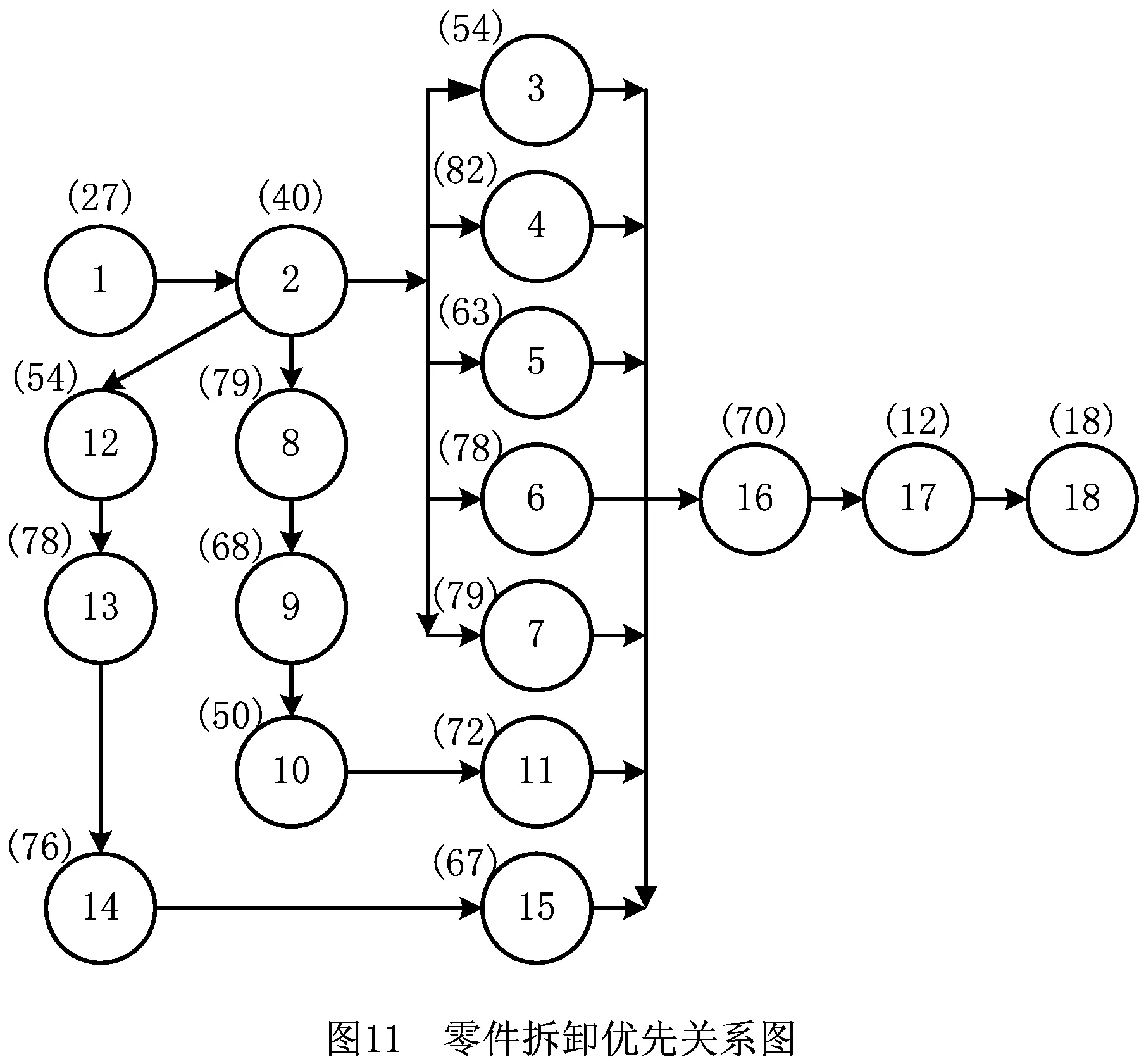
某再制造企业需要一批轴、齿轮轴及齿轮等废旧零件，该企业从回收商处购得一批废旧减速器(如图10)，并选择了专业拆卸服务企业对其提供拆卸服务。对减速器进行检测、评估后，该企业综合考虑减速器零件之间的拆卸约束条件和拆卸工艺要求，拟采用直线型拆卸生产线进行拆卸，并制定了拆卸方案。图11所示为减速器零件拆卸任务优先关系图，给定节拍为CT=240 s，现场拆卸任务强度中等，减速器各零件拆卸任务所需时间均通过秒表采用测时法获得，各零件需求指标dm=(0,4,6,5,3,8,11,3,4,6,14,4,8,6,14,12,16,22)。

算法采用Microsoft Visual C++语言进行编程，并在配置为2.50 GHz Intel(R)Core(TM)4 GB内存的个人计算机上运行。每个案例运行10次，记录平均值。算法的终止条件为运行时间达到nt×nt×10 ms。

表5 算法求解结果对比

由表5可知，ITLBO算法所求得的解优于遗传算法。

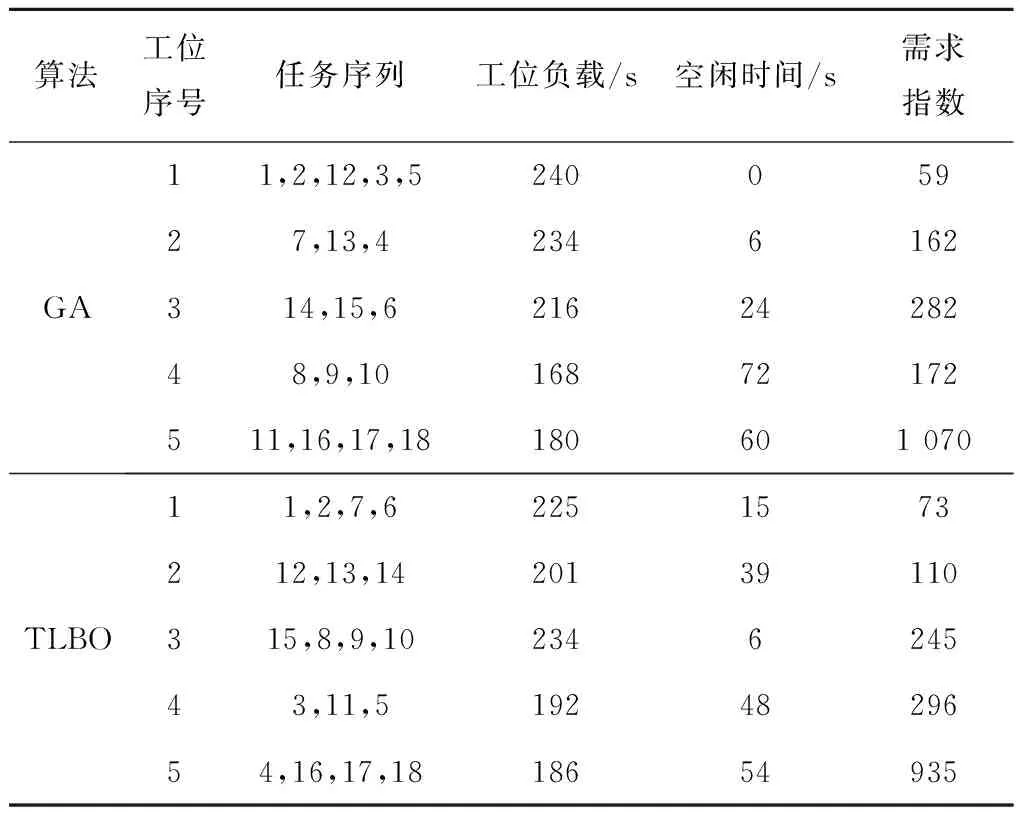
表6 减速器实例GA和TLBO求解的最优拆卸方案

由表6可知，实例中采用GA得到的工位数为5个，工位负载最大值为240 s，最小值为168 s，之间相差72 s，相对于给定节拍时间240 s，时差比例为30%，零部件需求指数之和为1 745；而采用改进型TLBO算法得到的工位数为5个，工位负载最大值为234 s，最小值为186 s，之间仅相差48 s，相对于给定节拍时间240 s，时差比例仅为20%，部件需求指数之和仅为1 659。由上述结果分析可知，所提出的改进型TLBO算法在求解RM-DS生产线平衡问题上具有优越性。

6 结束语

根据再制造服务的理念，提出了RM-DS的概念，在分析拆卸服务模式及各服务模式下拆卸服务生产线的特点和布局方式的基础上，为了提升RM-DS的资源利用率和拆卸服务生产线的整体效率，针对典型单产品批量拆卸服务模式中的直线型DLBP，建立了单产品直线型拆卸服务生产线平衡优化模型,并针对该模型特点提出一种无复杂参数设置的改进型TLBO算法。在基于随机键法初始化后，通过选择教师、教师教学、互学习局部优化和自学习增强型局部优化4个阶段的优化求解，得到更好的全局最优解。采用ITLBO算法和GA分别对两个经典案例(文献[21]中10个任务的拆卸实例和文献[9]中的52个任务的高速电子套结机拆卸)进行了拆卸生产线平衡优化分析，求解结果证明，改进型TLBO得到的最优拆卸序列的工位负载平衡率高于传统GA，验证了改进型TLBO算法在求解拆卸服务生产线平衡问题中的可行性和有效性。以减速器拆卸为工程实例，给出了所提模型与算法的具体应用。

本文研究为面向批量再制造的拆卸服务生产组织和优化研究提供了一种思路，后期将继续研究不确定拆卸时间及混流拆卸等拆卸线平衡问题。