带奇点的各向异性Moser-Trudinger不等式
胡 彬, 陈火弟
(东华理工大学 理学院,江西 南昌 330013)

(1)

各向异性的Moser-Trudinger不等式也是Moser-Trudinger不等式的一种推广形式。设F(x)是正的凸的一次齐次函数且F∈C2(n
1 预备知识
设F(x)∈C2(n)
Fξi(u)),当F(x)≠|x|时,上述算子是非线性的。把这些非线性算子称为Finsler-laplacian算子(也称为各向异性的Laplacian算子)。这类算子已取得了不少研究成果(Alvino et al.,1997;Ferone et al.,2009)。
考虑映照φ∶Sn-1→n,φ(ξ)=Fξ(ξ),其中Fξ=(Fξ1,Fξ2,…,Fξn)。则象集φ(Sn-1)是n上光滑的凸超平面,称之为F的Wulff形。设集合K∶={x∈n∶F(x)≤1},定义支撑函数F0(x)∶(x,ξ)。显然F0(x)也是C2(n

(2)

下面给出函数关于F0的凸对称定义。凸对称是Schwarz对称,参考(Talenti,1976)。考虑Ω⊂Rn上的可测函数μ的一维递减重排μ*=sup{S≥0∶|{x∈Ω∶|μ(x)|>s}|>t,t∈。
函数μ关于F0的凸对称定义为μ#(x)=μ*(κnF0(x)n),x∈Ω*。这里κnF0(x)n是同位于半径为F0(x)的Wulff球的Lebesgue测度,Ω*是中心在原点的wulff球且与Ω有相同的测度。由Alvino等(1997,2009)可知:
引理1 关于凸对称化函数u*,有以下结论:

(3)
2 主要结论的证明
本文把各向异性的Moser-Trudinger不等式,推广到带一个奇点的各向异性Moser-Trudinger不等式。得出以下结论:


(4)
同时

(5)
为方便证明记|Ω|=|WR(0)|(|·|为Lebesgue测度)。不等式(4)只是运用Hölder不等式的简单结果。实际上,对满足βt





设u#(r)是u关于F0(x)的凸对称重排(r=F0(x)),根据余面积公式,可得


(6)
再利用Hardy-Littlewood不等式和余面积公式,可得

(7)


(8)
并且
(9)
综合式子(6),(7),(8)和(9)得到

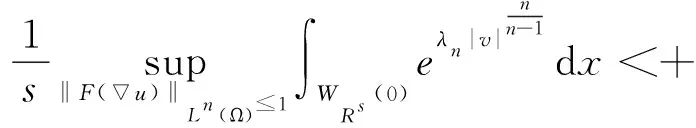
(10)

(11)
计算得到

并且


3 结论
本文利用余面积公式与凸对称重排法把各向异性的Moser-Trudinger不等式推广到带一个奇点的各向异性的Moser-Trudinger不等式,并最终证明了此不等式。

