基于自适应遗传算法的战场资源动态调度模型及算法
孙 鹏, 武君胜, 廖梦琛, 张杰勇
(1. 西北工业大学计算机学院,陕西 西安 710072; 2. 西北工业大学软件与微电子学院,陕西 西安 710072; 3. 空军工程大学信息与导航学院,陕西 西安 710077; 4. 中国人民解放军95445部队,云南 大理 672100)
0 引 言
战场平台资源调度问题研究在一系列约束条件下如何将军事组织拥有的平台资源合理的分配给作战任务,以实现作战目标的最优化[1-3]。如何灵活有序的调度作战资源是现代战争取得胜利的关键要素,也是实现作战任务规划的重要内容。
关于战场平台资源调度问题的优化模型和求解方法,Levchuk等人建立了以最小化使命完成时间为目标的问题模型,提出了多维动态列表规划(multidimensional dynamic list scheduling, MDLS)求解算法[4];文献[5-6]在此基础上分别考虑了完成时间约束和时间窗口约束,提出了循环MDLS和扩展MDLS求解算法;文献[7]以任务执行效率为目标函数建立了问题模型,通过量子遗传算法对问题进行求解,文献[8]建立了以最小化全部任务的完成时间和最大化平台资源利用率为目标的数学模型,结合蚁群算法解决平台资源的调度问题;文献[9]考虑了作战过程中战场环境中执行时间不确定、平台资源能力损耗不确定等因素,建立了以最大化使命成功概率为目标的机会约束规划模型,并提出了分散搜索算法求解该问题;文献[10]针对资源不确定性提出了资源缓冲区预测调度算法,为组织提供多个资源缓冲区分配方案;文献[11]进一步从多个方面考虑不确定因素,建立了以任务执行效率为目标函数的数学模型,求解不确定环境下的资源动态调度问题。
随着作战环境日趋复杂多变[12-13],战场平台资源调度问题的研究方向正逐渐从战前的预先调度向战时的实时调整转变[14-16],战场平台资源的动态调度成为了当前研究的重点。为此,本文研究了不确定环境下的战场资源动态调度问题,以最小作战完成时间为目标建立战场平台资源动态调度数学模型,并针对该问题模型的特点,基于自适应遗传算法进行求解。
1 平台资源调度问题的相关概念
1.1 作战任务
作战任务是指由作战使命分解得到需要执行的一系列子任务。记包含N个任务的任务集为T={T1,T2,…,TN},每个任务均具备以下属性:①任务持续时间LTi;②任务的地理坐标位置TPi=(xi,yi);③任务资源需求向量Ri={Ri1,Ri2,…,RiL},其中Ril表示成功处理任务Ti所需要的第l种类型资源的数量,L表示处理该任务所需要的不同类型资源的数量。
任务集合T中,任务之间通常存在一定的时序关系,即一个任务必须满足以下两个条件才能被处理:①该任务的所有前序任务已经全部完成;②处理该任务的所有平台资源已经到达该任务所处的位置。
1.2 平台资源
平台资源是指军事组织所拥有的具备处理作战任务的能力的基本单元。记包含J个平台的平台集为P={P1,P2,…,PJ},每个平台具备以下属性:①平台的初始地理坐标位置PPi=(xj,yj);②平台在不同任务之间转移时的移动速度vpj;③平台资源能力向量rj={rj1,rj2,…,rjL},其中rjl表示平台Pj提供的第l种类型资源的数量。若rjl=0,则说明该平台不提供第l种类型的资源。当平台Pk执行完任务Tm后被分配执行任务Tn,则平台从坐标(xmi,ymi)转移到坐标(xni,yni)所花费的时间((xni—xmi)2+(yni—ymi)2)1/2/vpj,当平台Pk到达所要执行的任务Tn的位置后,如果该任务只由一个平台Pk执行,则任务Tn在平台Pk到达后立刻开始执行;否则,Pk将等待其他平台达到后才能执行任务Tn。
1.3 平台资源调度方案
平台资源调度方案体现了军事组织所拥有的平台资源与作战任务之间的匹配关系,反应了作战任务被执行的情况。资源调度方案可用矩阵t′表示,其中t′表示任务Ti与平台Pj的处理关系,若Pj执行任务Ti,则t′=1,否则t′=0。本文选用作战使命的完成时间TFT为衡量资源调度方案优劣的测度值,对于任意任务Ti,任务的开始时间为BTi,任务的持续时间为LTi,则任务的结束时间ETi=BTi+LTi,因此,作战使命的完成时间与最后一个任务的完成时间有关,表示为
TFT=max(ET1,ET2,…,ETN)
2 平台资源动态调度模型
2.1 使命环境中不确定性的表示
受到战场的复杂环境的影响,使命在执行过程中可能会因为诸多不确定因素而使平台资源的属性、作战任务的属性发生变化。不确定性引起的变化可能导致初始的资源调度方案不能按照原计划执行,或是执行效果与预期效果存在较大的偏差,因此需要对作战方案进行调整,使其满足当前的作战需求。作战过程中,本文设计只考虑以下两方面的不确定性事件:
(1)突发任务。突发任务是指在使命执行过程中某一时刻临时增加的不属于初始任务集中的任务。这一任务的出现,要求使命执行过程中必须临时分配新的平台资源来执行该任务。
(2)平台失效。平台失效指随着作战进程的继续,平台资源出现故障或受到敌方打击而无法继续提供任务需求的各项资源能力的情况。
当以上两方面不确定事件发生后初始的资源调度方案可能已不再满足当前作战实际情况的需求,因此需要对资源调度方案进行调整。调整过程也要满足两方面的需求:①尽量降低资源调度方案的调整幅度,以维持原有调度方案的稳定性;②未受到影响的作战任务维持原始的资源调度方案不变,以降低军事组织的结构调整代价。
2.2 约束条件分析及模型建立
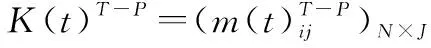
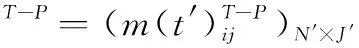
(1)

为了使组织调度方案的代价尽可能小,调整过程必须满足以下约束条件:
(1) 受不确定事件影响的任务集合记为T(t′),此时新增加的任务集合为Tnew=T(t′)-T(t)。为了尽量降低组织结构调整代价,对新增加的作战任务能分配到的平台资源数量进行限制,表示为
≤M
(2)

(2) 未受到影响的任务集合表示为Tnomal=T(t′)-Tnew-Tdestroy,其中Tdestroy表示因平台摧毁而受影响无法正常执行的任务。未受影响的任务对应的平台资源调度方案按照原始分配方案继续执行,表示为
,Tk∈Tnomal
(3)
(3) 任务的资源满足度指作战平台实际提供的资源能力与任务预计需求的资源能力之间的比值,表示为
(4)
平台资源在处理作战任务时,平台提供的各项资源能力与任务各项资源需求的比值,体现了任务的完成质量,表示为
(5)
式中,γ(i)表示处理任务i所需要的不同类型的资源;‖γ(i)‖表示任务Ti所需要的资源类型总数。
任务集中的每一个任务都必须达到一定的任务完成质量要求,即
Qk≥δ,Tk∈T(t′)
(6)
综合上述约束条件,以最小使命完成时间为优化目标,建立的平台资源动态调度模型可以描述为
min TFT
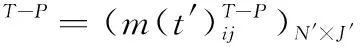
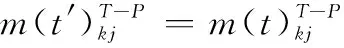

Qk≥δ,Tk∈T(t′)
(7)
3 模型求解算法
由式(7)可知,平台资源的动态调度是一个组合优化问题,考虑到智能搜索算法能够较好地求解该类问题,因此,本文选择基于自适应遗传算法进行模型求解。
自适应遗传算法是基于遗传学原理的随机并行搜索算法,该算法能在不需要任何初始化信息的条件下实现对最优解的全局搜索,可以有效解决带约束条件的二元规划问题,与传统遗传算法不同,自适应遗传算法根据每代个体的适应度值适应的调整交叉、变异概率,一方面保证了种群的多样性,另一方面保护了种群中的优良个体不受到破坏。打破传统遗传算法容易陷入局部最优的僵局,使算法的全局搜索能力更强。
3.1 染色体的编码方法
当突发事件发生后,将受到影响或新增的任务放入待优化任务集合δ中。此时待优化任务集中存在δ个任务等待分配平台资源,其中,每个任务Ti(i=1,2,…,δ)对应的编号为i。若集合δ中有多个任务,则集合中任务的优先权按照任务的开始时间BTi进行排序,开始时间越早优先级越高。对于每一个平台Pj(j=1,2,…,J)而言,它的状态s(j)有两种,若该平台被分配执行当前待优化的任务Ti,则状态s(j)=1,若未分配给当前的待优化任务Ti,则状态s(j)=0。
一个染色体对应一种当前待优化任务Ti的平台调度方案,并且每个平台被分配执行任务的编码是不连续的一串0-1二元变量,因此,可以采用离散二元0-1整型的编码方式对GA的染色体进行编码:一个染色体是一个由J个0-1二元整数构成的有序序列S={s(1),s(2),…,s(J)},其中,s(j)∈{0,1}。
3.2 适应度函数
根据上述对染色体编码的方式可知,染色体中可能存在一部分不可行的平台资源调度方案,即当前待优化任务Ti的完成质量在新的调度方案下无法达到最低质量δ的要求。因此,在计算各个染色体的适应度之前,要对每一个染色体对应的资源调度方案的可行性进行判断,如果在该方案下当前待优化任务Ti的完成质量未达到最低质量δ的要求,则将该染色体的适应度值设置为0。对于可行的染色体,选择模型中目标函数的倒数作为其适应度函数。由此可知,本文自适应遗传算法(self-adaptive genetic algorithm, SGA)算法的适应度函数表示为
(8)
3.3 遗传算子
3.3.1 交叉、变异算子
种群的交叉概率Pc、变异概率Pm与种群的规模、适应度值分布相关。在算法前期,交叉、变异概率较大,以丰富种群的多样性,提高搜索能力,算法后期,降低交叉、变异概率以保护最优个体不受到破坏。
因此,交叉概率为
Pc=
(9)
变异概率为
Pm=
(10)
式中,Pc2和Pm2是固定值,交叉概率参数Pc1和变异参数Pm1是随进化代数N变化的参数,满足
(11)
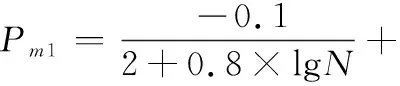
(12)
式中,N为进化代数,参数φ和φ表示交叉概率参数和变异概率参数的收敛极限。
通过引入正弦变化形式对交叉变异概率进行自适应调整,可以避免当适应度值接近最大适应度值或者平均适应度值时交叉、变异概率过大或者过小,克服种群“停滞”而陷入局部最优的情况。同时,在算法初期,较大的交叉概率能够保证种群的多样性,全局搜索能力更强;算法后期降低交叉概率提高变异概率,在维持种群最优个体的同时从一定程度上抑制算法的过早收敛。
3.3.2 选择算子和精英保留策略
本文通过轮盘赌选择法保留适应度值较高的个体,在由初始种群、经过交叉、变异得到的种群合并成为新的种群中进行筛选,淘汰适应度值较低的个体。同时采用精英保留策略,遗传操作过程中继承父代的优良个体,保证每一代产生的最佳染色体能够保留下来。
3.3.3 SGA的整体步骤
步骤1采用本文设计的染色体编码方式,随机产生初始种群GI,种群规模为Num;
步骤2采用本文设计的交叉算子和变异算子,对GI进行概率为Pc的交叉操作、行概率为Pm的变异操作,分别产生交叉种群Gc和Gm;
步骤3将GI、Gc和Gm合并一个种群,采用本文设计的选择算子,进行选择操作,产生种群规模为Num的新一代种群,并将其替代初始种群GI;
步骤4重复步骤2至步骤3直至达到最大迭代次数N。
4 算例分析
本文以一个联合作战想定为算例进行模型合理性和算法有效性的验证,作战任务的属性与组织拥有的平台资源属性分别如表1、表2所示,共包含作战任务N=8个,平台资源J=12个。
初始平台资源调度方案如图1所示,设置新增任务的平台资源限制数M=3个。

表1 作战任务属性表
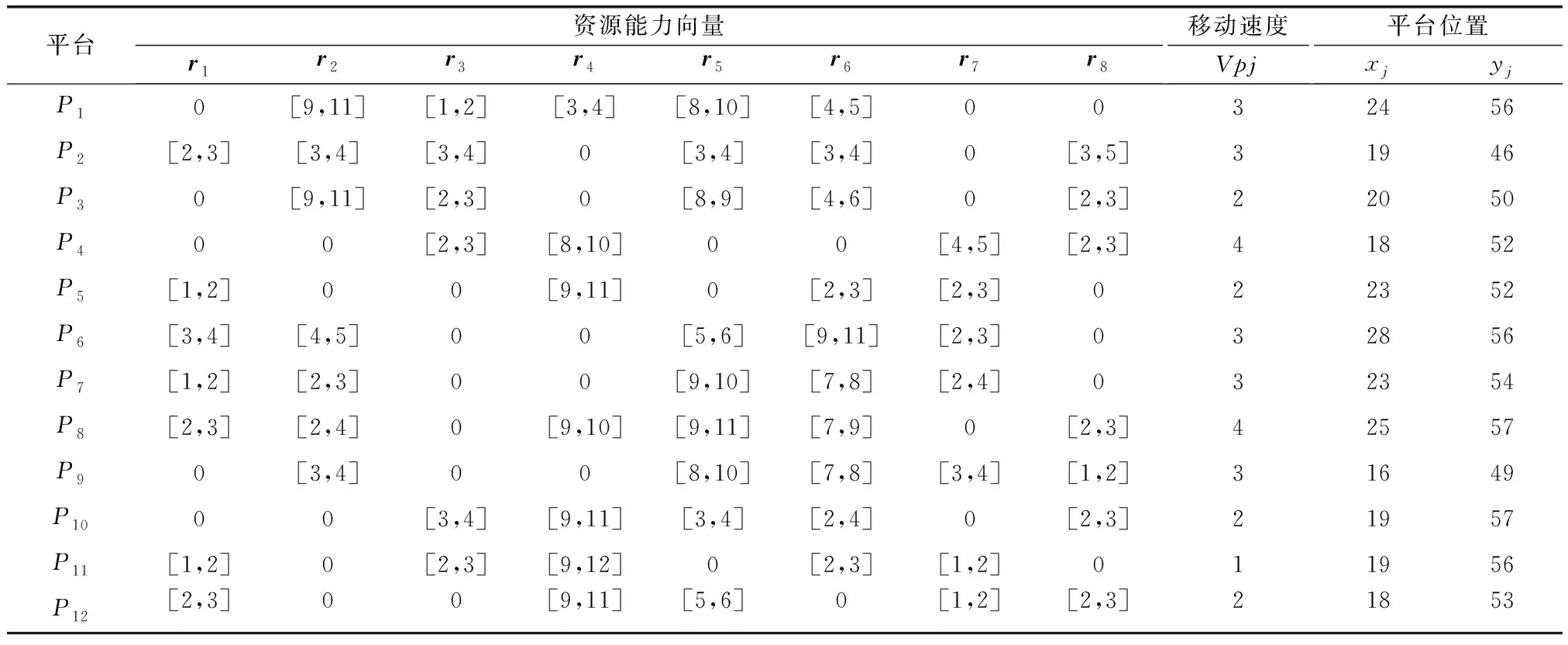
表2 平台资源属性表
算例中SGA算法的参数设置为初始种群规模Num=40,初始交叉概率Pc2=0.8,初始变异概率Pm2=0.1,交叉概率参数φ=0.8,变异概率参数φ=0.13,进化代数N=100。
针对以上算例,进行下仿真实验:
仿真实验1令任务的质量最低完成参数δ=0.8,作战使命按照初始资源调度方案执行至t=50时刻时,突发事件1发生,新增任务T9出现,出现的位置在任务时序列表中的任务T8执行完成后、任务T2执行开始前,任务位置的坐标TP9=(32,59),任务持续时间LT9=10,资源能力需求向量R9={0,7,3,0,6,2,0,2}。作战使命执行至t=77时刻时,突发事件2发生,平台P6被摧毁。利用SGA算法对两种突发事件情况下的资源调度方案进行调整。调整后的平台资源调度方案甘特图如图2所示。

图2 突发事件1发生后的平台资源调度方案Fig.2 Platform resource scheduling plan after incident 1 occurs
当突发事件1发生时,任务T9将被分配平台资源以保证执行。通过SGA算法得到的最优解染色体编码为{1,0,1,0,0,0,0,0,0,0,0,0},适应度值为0.007 81,函数值TFT=127.97,从结果可知,对于新增任务T9选用平台P3、P6执行能使调整后的整体使命完成时间比较调整前增加了9.84,此时任务T9的完成质量为0.96。
当突发事件2发生时,平台P6被摧毁。在t=77这个时刻P6没有执行任务,但是后续T5任务已经分配平台P6,且P6摧毁后该任务的完成质量为0.77,不满足最低任务完成质量要求,因此需要为T5分配新平台资源。通过SGA算法得到的最优染色体编码为{0,0,0,1,0,0,0,1,1,0,0,0},表示新增平台P9,和原方案中的P4、P8共同执行任务T5,该染色体的适应度值为0.007 64,函数值TFT=130.82,调整后的平台资源调度方案如图3所示。
以上结果表明,当突发事件发生后,为了保证受影响任务的完成质量,同时又要保证整体使命执行时间最短,调整执行受影响任务的平台资源必须满足以下两个方面要求:一是单个平台尽可能的满足当前待处理任务的资源需求;二是平台此时的坐标位置与当前待处理任务的坐标位置距离相近,这样能够保证平台移动的时间最短。
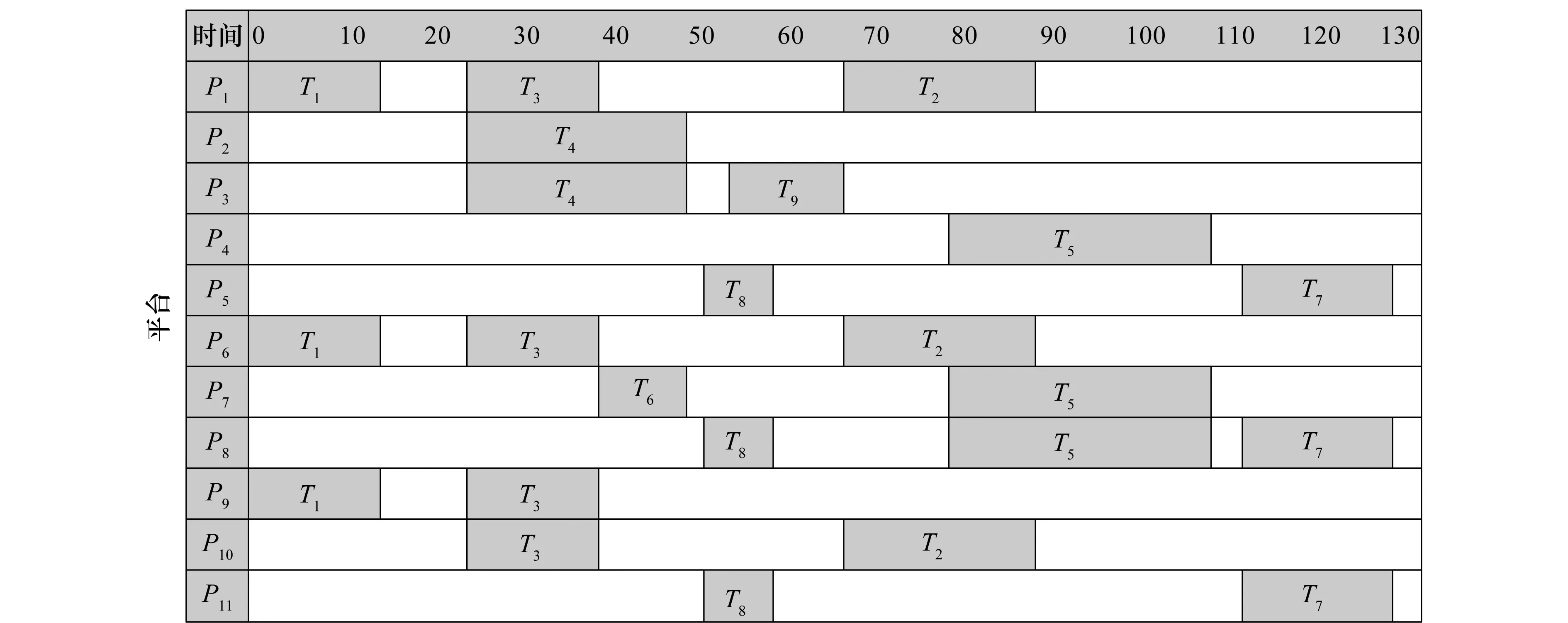
图3 突发事件2发生后的平台资源调度方案Fig.3 Platform resource scheduling plan after incident 2 occurs
仿真实验2当t时刻触发资源动态调度时,随机生成突发事件及相应属性,采用SGA算法对该模型进行求解,将最低任务完成质量δ设置在区间[0.5,1]内,Δδ=0.5,随机进行4组实验,所得到的使命完成时间TFT与最低完成质量δ之间的变化曲线如图4所示。
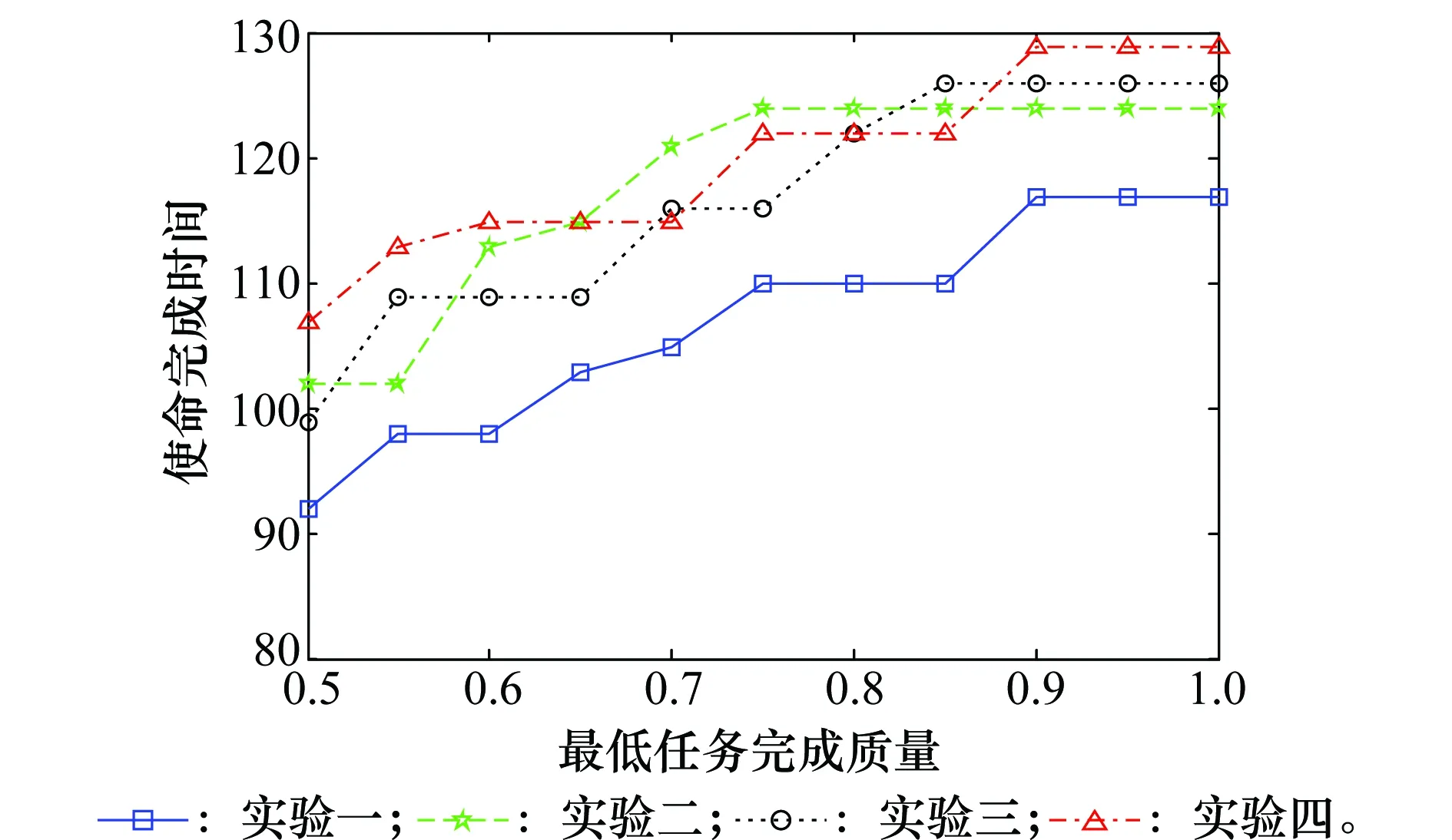
图4 最低任务完成质量与作战完成时间的变化曲线Fig.4 Operational completion time curve with the minimummission completion quality
图4中,每条不同的曲线代表不同的实验组。从图中4条曲线变化的趋势可以看出,随着任务完成质量要求δ的不断提高,使命完成时间均不断延长,这是因为随着任务完成质量要求的改变,更多的平台资源需要向受到影响的任务移动,平台在移动过程中会增加使命完成的耗时。并且为了降低军事组织的组织调整代价,使未受到影响的作战任务的资源调度方案维持初始不变,当一些平台资源被分配执行突发任务时,初始分配的任务则后延执行,因此使命完成时间普遍增加。受到组织拥有的平台资源数量的限制,没有足够的冗余平台执行突发任务时,使命整体完成时间被延长的现象较为严重,这也进一步反映出当平台资源不充足而任务完成质量要求又较高时,难以维持组织的鲁棒性。
从图4中也可以看出,随着任务完成质量要求的不断增加,使命完成时间并不总是延长的,这是因为平台资源能力与任务资源需求均为离散的数值,在任务执行过程中其完成质量在一定范围内变化时并不需要对资源调度方案进行反复调整,因此使命完成时间对应某些要求时可能不发生变化。
仿真实验3为了验证本文所提的SGA算法在解决资源动态调度问题上的优越性,将SGA算法与模拟退火算法(simulated annealing, SA)进行对比,设置最低任务完量δ=0.8,突发事件的发生时刻用蒙特卡罗方法随机生成,随机进行10组仿真实验,所得结果如图5所示。
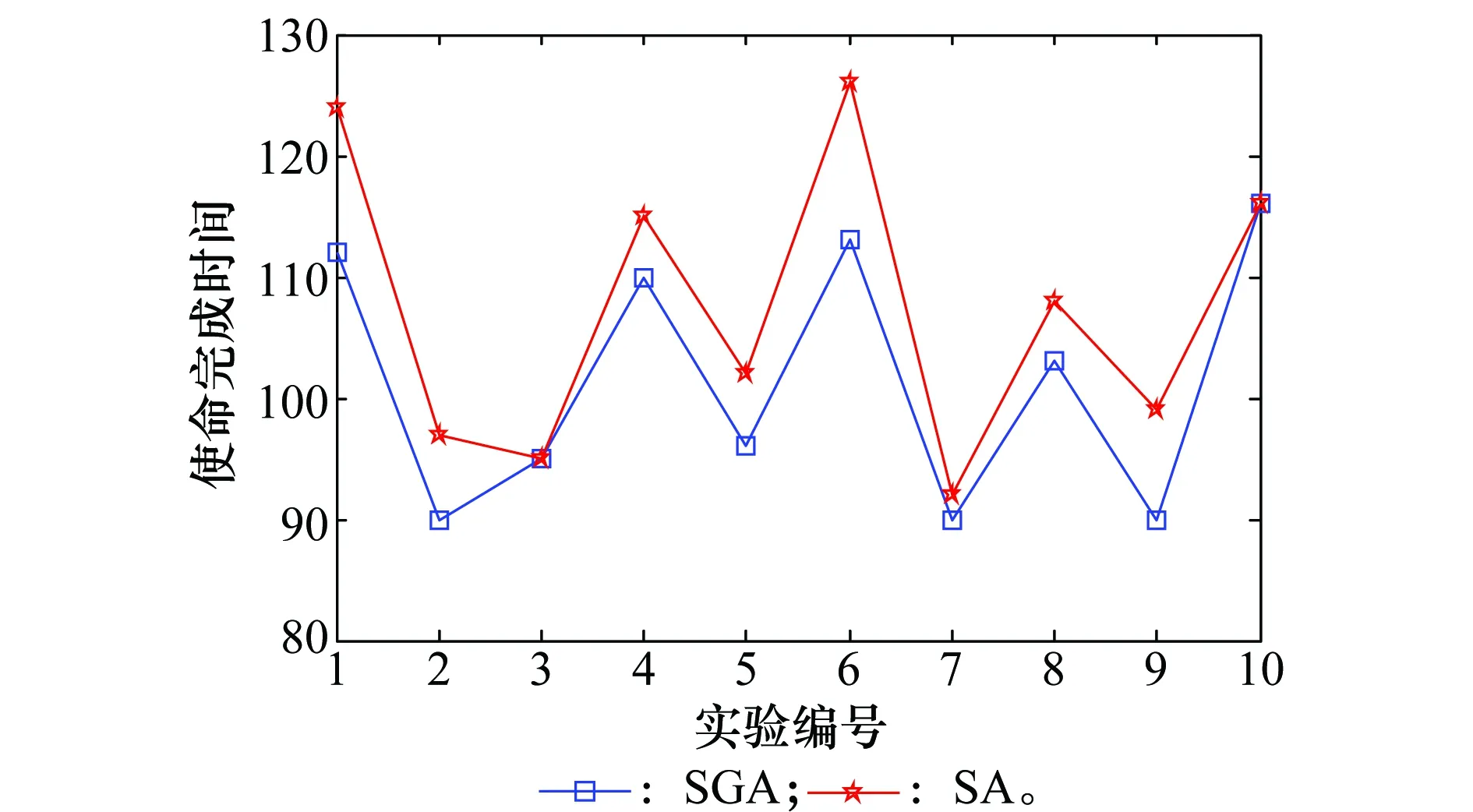
图5 算法比较Fig.5 Algorithm comparison
从图5中可知,SGA算法得到的平均使命完成时间TFT=101.53,SA算法得到的平均使命完成时间TFT=107.41,虽然在部分实验组中,两种算法得到的结果相同,但整体而言,SGA得到的使命完成时间优于SA算法的结果,也即本文算法在解决平台资源动态调度问题时更为有效和优越。
5 结 论
本文描述了作战环境中的不确定性,分析了资源动态调度的约束条件,构建了以最小整体使命完成时间为目标函数的资源动态调度模型,通过SGA算法对由不确定性引起的作战任务或平台资源变化的突发事件进行资源调度方案的调整。基于联合作战算例的仿真结果表明,所建模型及其求解算法能有效的解决战场资源动态调度问题,并且可以有效的应对由战场不确定性引起的突发事件为目标的动态优化模型,设计了模型求解的SGA算法。基于联合作战算例的仿真结果表明,所建模型及其求解算法能有效解决战场资源动态调度问题,可以较好应对和处理战场的突发事件。下一步研究重点将从多个优化目标如任务执行精度、成功执行概率等角度考虑优化模型的构建,并进一步考虑资源的动态调整。

