基于DDBN-Cloud的舰艇编队防空目标威胁评估方法

孙海文, 谢晓方, 孙 涛, 张龙杰

(海军航空大学岸防兵学院, 山东 烟台 264001)

0 引 言

编队指挥员依据战场信息,对空中来袭目标对我编队构成的威胁度进行分析和排序,称为威胁评估[1]。在舰艇防空中,根据要保护对象数量的不同,可分为单舰防空(要保护舰艇数量为1)和编队(或称多舰)防空(要保护舰艇数量为2以上)。编队防空威胁评估与单舰防空威胁评估不同,需要考虑编队内受攻击舰艇的重要性对评估来袭目标威胁度的影响,受攻击舰艇的重要性越高,则来袭目标威胁度就越高。

目前,对空中来袭目标进行威胁评估的常用方法有:多属性决策理论[2-4]、神经网络[5-6]、模糊理论[7-9]、粗糙集理论[10]、贝叶斯网络(Bayesian network,BN)[11-13]等方法。综合分析这些方法存在以下问题:一是在舰艇编队防空中,由于影响来袭目标威胁评估的因素较多,评估体系较复杂,而多属性决策理论和模糊理论通常不能很好的呈现出各评价指标的实际情况,使得评估结果不准确;二是来袭目标速度较快,留给武器系统的反应时间较短,对实时性要求较高,粗糙集理论需要建立庞大的知识库来支持相关规则提出,会造成处理速度慢,难以保证实时性;三是当舰艇编队受到饱和攻击时,来袭目标数量较多,其信息量较大,往往出现粗大误差和数据缺失问题,神经网络方法建立的体系结构通用性差,无法适应动态变化的环境,当数据缺失时,无法正常工作。威胁评估是对战场上获得的数据流的高层次关系进行提取与处理,接近于人的思维过程。它涉及到众多因素,而且这些因素存在不完整、不确定的特性。贝叶斯网络能够有效处理不确定问题,但存在以下两个问题:一是该推理是基于先验概率,概率本身具有不确定性,导致其结果准确度较低;二是各网络节点均为离散变量,对连续型变量不能进行有效地推理。

综上所述,本文提出了基于离散动态贝叶斯网络-云模型(discrete dynamic Bayesian networks cloud, DDBN-Cloud)的舰艇编队防空目标威胁评估方法。结合实际情况,分析了舰艇编队海上防空的特点,建立了威胁评估指标体系,并利用模糊逻辑理论将指标体系中的连续型变量转化为离散型变量;在此基础上,建立了两级BN结构[14],将一个相对复杂的大系统推理网络分解为多个规模较小的推理子网络,使得同一级的子网络并行计算,提高了推理速度;针对评估过程中指标数据缺失问题,采用前向信息修补算法进行信息预测修补;对于观测数据的不确定性问题,采用可信度来处理;利用云模型在处理随机性和模糊性方面的优势[15-16],合理构建目标威胁等级云模型,通过正向云发生器逆运算将威胁评估概念转化为定量数据。最后,将DDBN-Cloud法与BN-Cloud法和相对熵排序法相比较,通过仿真实验验证DDBN-Cloud法的可行性和优势性。

1 建立评估指标

在海上编队防空作战中,威胁评估指标应根据舰艇编队中各类传感器探测和收集到的目标数据内容进行选取,且各指标应与威胁度有着直接或间接的关系。

建立编队防空来袭目标威胁评估指标[17]如图1所示。

图1 编队来袭目标威胁评估指标体系Fig.1 Index system of formation incoming target threat assessment

为了便于指挥员进行编队舰空导弹射击指挥决策,需要对空中来袭目标威胁等级进行划分。敌方来袭飞机和反舰导弹对我编队的威胁程度可分为3个等级,具体划分如下:

Ⅰ级威胁(高) 敌向我发射的反舰导弹和装备反舰导弹的飞机等,目标向我方移动速度较快且我方编队处于目标的攻击范围内,且具有明显攻击意图,必须立即采取对抗措施;

Ⅱ级威胁(中) 没有装备反舰导弹、只能使用普通航空炸弹或其他机载武器的飞机等,目标向我方移动速度较慢且我方编队处于目标的攻击范围内,目标没有明显攻击意图,能够采取对抗措施;

Ⅲ级威胁(低) 侦察机、预警机、反潜机等辅助作战飞机,处于防区外,我方无法采取对抗措施。

1.1 舰艇价值

在海上编队防空作战中,受攻击舰艇的重要性对评估来袭目标威胁度有影响,受攻击舰艇的重要性越高,则来袭目标威胁度就越高。编队内各舰艇的重要性要根据编队当前所执行的任务性质、编队内各舰艇在完成该任务的能力大小以及舰艇本身的重要性来确定,若设各舰艇重要性为Value1,Value2,…,Valuem,其中Valuej∈[0,1],m表示编队中舰艇总数量,那么编队总重要性为

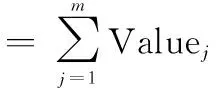
(1)

从而得到第j艘舰艇的相对重要性为

(2)

显然,δ(Valuej)值越大,该艘舰艇的重要性越高。

这里按照δ(Valuej)的大小划分舰艇重要性类型,将连续型变量转化为离散型变量。区间为(0,0.3],(0.3,0.7],(0.7,1],分别对应重要性类型为“低”、“中”、“高”。舰艇重要性指标应用于目标攻击意图的判别中。

1.2 目标类型

在编队防空作战中,不同的目标类型对舰艇的威胁度也不相同[18],随着编队防空作战范围的增大,其面临的目标也更复杂。根据目前对目标的识别能力,可将目标区分为导弹、大飞机、小飞机、直升机和空中不明目标等5类。具体分类如表1所示。

表1 目标类型

1.3 目标攻击意图

当反舰导弹攻击我舰艇编队时,如果目标企图攻击我编队内的某艘舰艇,则认为该目标对该舰艇产生威胁。通常情况下,敌对我编队的攻击意图可由目标舷角进行判断。假设任意时刻我编队内某舰艇j位于O点,反舰导弹i位于Ti点,目标舷角为θji,航向为Ci,据我舰距离为Dji,相对于我舰方位为φji,如图2所示。

图2 来袭目标攻击我舰艇示意图Fig.2 Sketch map of incoming target

则有

(4)

式中,tpyei表示第i个目标类型;attcakji表示第i个目标对第j艘舰艇的攻击意图。有攻击意图的取1,没有攻击意图的取0。

企图攻击编队内重要性越高的舰艇,攻击意图的威胁属性类型就越高。攻击意图的威胁属性类型为

(5)

根据受攻击舰艇重要性类型将攻击意图的威胁属性类型划分为“高”、“中”、“低”。

在实际过程中,可能出现来袭目标对编队内多个舰艇都有攻击意图,这里选择目标舷角最小的舰艇作为被威胁对象,若目标相对多艘舰艇舷角相同,则根据悲观原则选择重要性高的舰艇为被威胁对象;对于飞机类目标,由于其发起的攻击距离远,机动范围大,当其目标舷角大于90°,并不意味其对我方没有威胁意图,这里将其威胁属性类型划分为“中”。

1.4 目标攻击高度

目标高度是指目标距海平面的垂直距离。利用模糊逻辑理论将连续型变量转化为离散型变量[19],根据(0,0.2],(0.2,0.4],(0.4,0.6],(0.6,0.8],(0.8,1]区间划分对应的攻击高度威胁属性类型为“低”、“较低”、“中”、“较高”、“高”。

1.5 目标接近速度

目标径向速度是指目标相对要攻击舰艇的相对速度。利用模糊逻辑理论将连续型变量转化为离散型变量[19],根据(0,0.2],(0.2,0.4],(0.4,0.6],(0.6,0.8],(0.8,1]区间划分对应的接近速度威胁属性类型为“低”、“较低”、“中”、“较高”、“高”。

1.6 拦截目标的剩余时间

目标相对编队的剩余拦截时间是指目标从当前位置以当前速度穿越编队舰空导弹综合发射区所需的时间,等于目标在编队舰空导弹综合发射区内飞行总距离与目标速度比值。利用模糊逻辑理论将连续型变量转化为离散型变量[19],根据(0,0.2],(0.2,0.4],(0.4,0.6],(0.6,0.8],(0.8,1]区间划分对应的拦截目标的剩余时间威胁属性类型为“低”、“较低”、“中”、“较高”、“高”。

1.7 目标的毁伤能力

毁伤能力即目标命中我编队舰艇后我舰艇所受的损伤程度。舰艇完全丧失能力所承受的弹药数Ntype,其值由指挥员或专家确定[20]。毁伤能力类型分为“低”、“中”、“高”。

2 基于DDBN-Cloud模型的威胁评估方法

目标来袭过程中各观测数据随时间推移而发生变化,其威胁评估过程属于动态的过程,因此该方法充分利用了DBN在随时间变化的不确定信息环境中的推理能力[21-22]。采用前向信息修补算法对评估过程中的缺失数据进行预测修补;根据专家知识或贝叶斯参数学习确定网络结构中的条件及转移概率;对于各观测节点数据存在一定的不确定性问题,引入可信度来进行处理,使得网络参数更符合实际情况;利用云模型处理定性概念与定量数值之间转化的能力,将威胁评估等级转化为云模型,再利用概率-确定度转化方法,求得目标具体的威胁值,进行威胁排序。

2.1 建立DDBN威胁评估模型

本文将动态贝叶斯威胁评估网络拆分为两级决策子网络。第1级对应威胁度评估子网络;第2级对应目标攻击能力评估子网络。这样就将一个相对复杂的大系统推理网络分解为多个规模较小的推理子网络,使得同一级的子网络并行计算,提高了推理速度;同时,分级结构能明确各因素在威胁评估中的主次地位,使得BN结构推理更合理。

第1级网络为威胁度评估网络如图3所示。

图3 一级动态贝叶斯网络Fig.3 First level DBN

第2级网络为攻击能力评估网络,如图4所示。

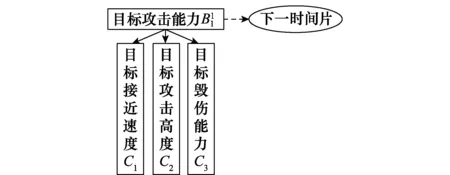
图4 二级动态贝叶斯网络Fig.4 Two level DBN

这里要获取隐藏在模型节点之间的关系即获取条件概率表(conditional probability table, CPT),有两种方式:

方式1根据实际记录的数据,利用期望最大化算法(expectation-maximization,EM)[23-24]进行贝叶斯网络参数学习,进而获取CPT。

方式2根据专家经验知识来获取CPT。

在缺少实际数据的情况下,这里根据专家经验知识来获取CPT。

2.2 信息修补

DBN的信息能够沿着网络向前传播,即前面时间片的证据信息会对后面的时间片产生影响。基于这种信息传播规律,提出了前向信息修补算法的基本思想:假设前n个时间片的缺失数据已经得到修补,如图5所示,A区的观测节点(灰色节点)是由直接观测到的证据信息节点(实线灰色节点)和缺失证据信息得到修补后的观测节点(虚线灰色节点)组成,即前t个时间片的证据信息是由直接观测到的证据和修补得到的证据组成的混合证据信息。现在要修补第t+1个时间片的缺失数据(虚线白色节点),根据第t个时间片所获得的混合证据信息计算第t个时间片隐藏Xt的后验概率,再借助转移概率把第t个时间片隐藏变量的后验概率映射到下一时间片,即对下一时间片的隐藏节点Xt+1的状态进行预测,然后把预测转化为对缺失证据信息的预测,以此预测值代替缺失数据。

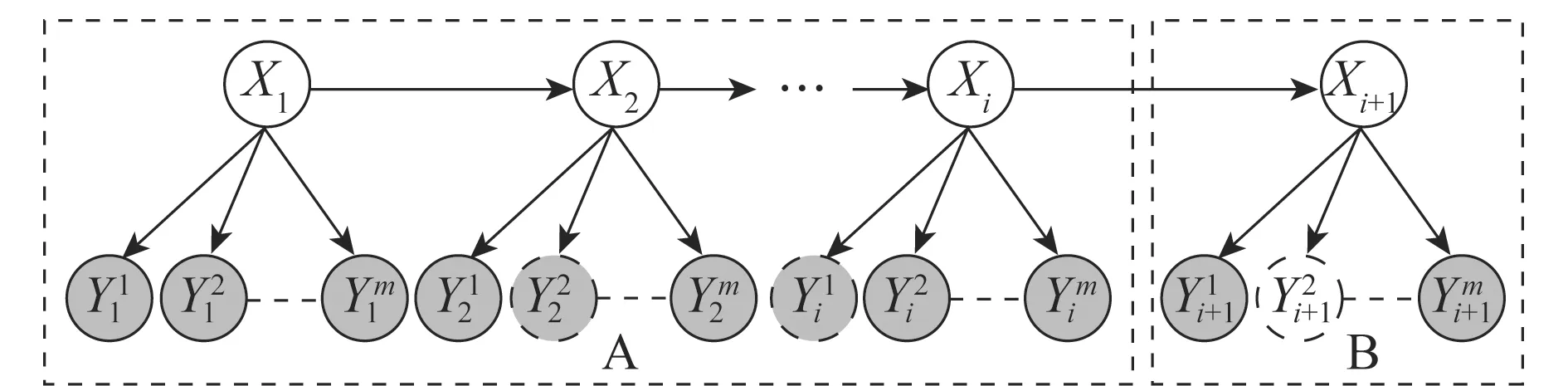
图5 前向信息修补算法的修补过程示意图Fig.5 A schematic diagram of the forward information repairalgorithm patching process

具体修补步骤如下:

步骤1根据给定的初始状态概率、条件概率和转移概率初始化网络,设定离散动态贝叶斯网络的时间片数为T。

步骤4令,若v≤m转入步骤2,否则,取t=t+1,转入步骤5。

步骤6定义前向传播算子为αt(j),递归公式如下。

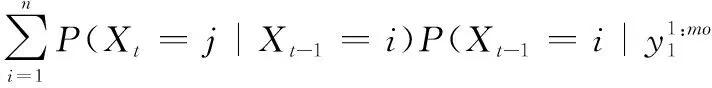
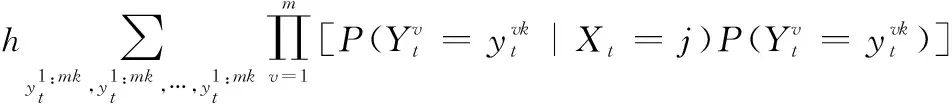
(6)

在式(6)的基础上,对下一个时间片的隐藏变量状态进行预测,即

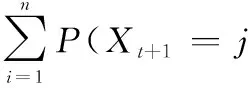
(7)

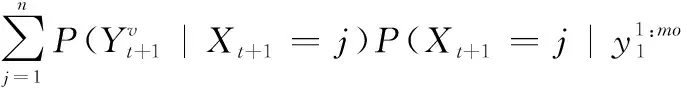
(8)

步骤7令v=v+1,若v≤m转入步骤5;否则,令t=t+1;若t≤T,则转入步骤5,否则结束。

该信息修补算法既能处理确定性证据,又能处理不确定性证据。其利用部分证据信息对缺失数据进行修补,计算量较小。

2.3 不确定性处理

BN结构中,证据节点B2、B4和C3的取值是来自传感器的测量或是人为推断,在实际防空作战中,敌方利用反侦察、伪装、欺骗等行为对我方进行限制干扰,所以观测结果与实际结果之间存在一定的不确定性。本文利用证据节点与实际节点之间的条件概率来表示两者之间的不确定性关系。假设用Evik来表示证据节点类型,用Acti表示实际节点类型,k和i都代表相应的类型。证据的可信度定义为实际结果与观测结果相符合的程度。即

P(Acti/Evii)=ai,i∈(1,2,…,n)

(9)

P(Acti/Evik)=bik,i≠k且k、i∈(1,2,…,n)

(10)

当观测结果类型为typei时,实际结果也为typei的可能性为ai,即可信度。该值由实际作战经验、传感装备性能以及专家知识获得,其结构如图6所示。

图6 引入可信度的节点结构图Fig.6 Node structure diagram with introducing credibility

在BN中,需要得到实际节点与证据节点的条件概率表,令

P(Acti)=ci,i∈(1,2,…,n)

P(Evik)=dk,k∈(1,2,…,n)

式中,ci为已知概率,dk为未知概率,根据贝叶斯定理得

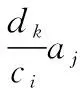
(11)

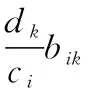
(12)

(13)

由式(11)～式(13)可求得dk,将dk代入式(11)和式(12)可求得实际节点与证据节点的CPT。

2.4 建立云模型

利用云模型的3个数字特征(Ex,En,He)将威胁等级的定性描述语言转化成云模型。

定义威胁值域为U,且U=[0,1],U1、U2、…、Un为U的子域,分别代表威胁的n个等级。这些子域满足下列条件:

条件2在各子域的Ex处,其他域的确定度为0;

条件3各子域交点确定度小于33.3%。

设ui∈Ui,则ui对Ui的确定度为μUi(ui),且μUi(ui)∈[0,1]。云模型用Cui表示,云滴表示为drop(ui,μUi(ui))。

根据威胁度的3个等级,分别建立3个云模型,云模型遵循“3En规则”,即区间[Ex-3En,Ex+3En]对云模型所表达的定性概念的贡献达到99.74%。

设某一威胁等级区间为[e,f],采用指标近似法[25]确定模型的特征参数,即

(14)

这里设计威胁等级低为半降正态云Cu1(0,0.17,0.01);威胁等级中为正态云Cu2(0.5,0.17,0.01);威胁等级高为半升正态云Cu3(1,0.17,0.01)。威胁等级云模型如图7所示。

图7 威胁等级云模型Fig.7 Cloud model of threat level

2.5 概率-确定度转化方法

每个威胁等级都对应着一个云模型,使得威胁等级概率与云模型的确定度相匹配。云的确定度不具备概率所具有的规范性,因而,本文采用如下方法来进行确定度与概率的转化,即

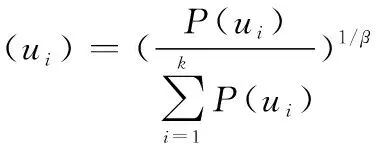
(15)

式中,μ(ui)表示确定度;P(ui)表示概率;β是衡量确定度与概率一致性的常数,β∈[0,1],β越大,两者一致性越强。本文取β=1。

2.6 求解威胁度

在云模型中,云发生器用于转化定性概念与定量数值,其分为正向云发生器和逆向云发生器两类:正向云发生器,实现从定性概念到定量数值的映射;逆向云发生器,实现从定量数值到定性概念的映射。这里使用正向云发生器,在已知定性概念的数字特征(Ex,En,He)和确定度λ,利用逆运算来求取确定度对应的威胁度。具体实现步骤如下:

步骤1生成一个以En为期望、He为标准差的一个正态随机数En′=NORM(En,He2);

步骤2计算确定度λ的特征值γ为

(16)

3 仿真试验

3.1 仿真条件建立

设某舰艇编队,有3艘舰艇组成单纵队,其中包括1艘驱逐舰(K1)、两艘护卫舰(K2、K3),驱逐舰位于编队中间,仿真时间长度取2.0s。假设得到时间片1、2的各观测节点信息如表2和表3所示,所对应的观测节点状态如表4～表5所示。

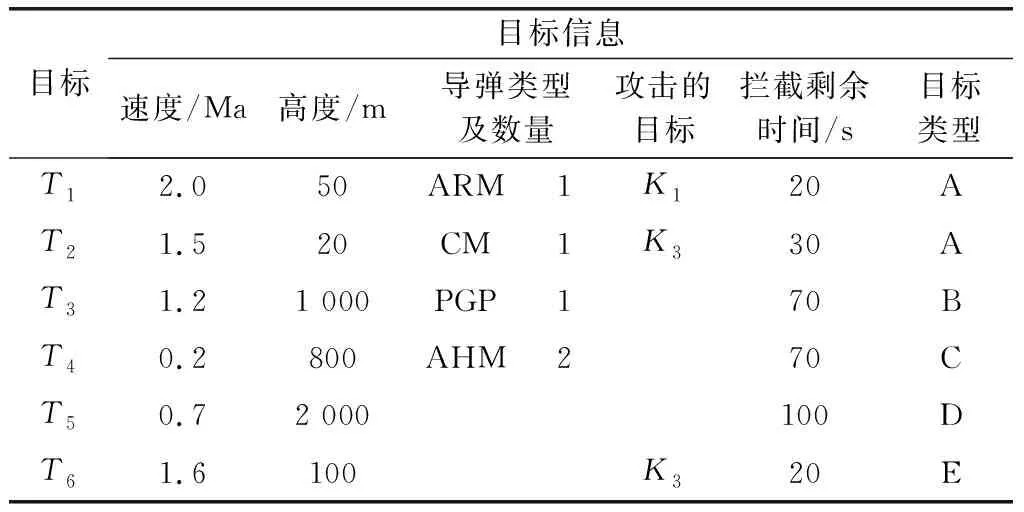
表2 时间片1下各来袭目标信息

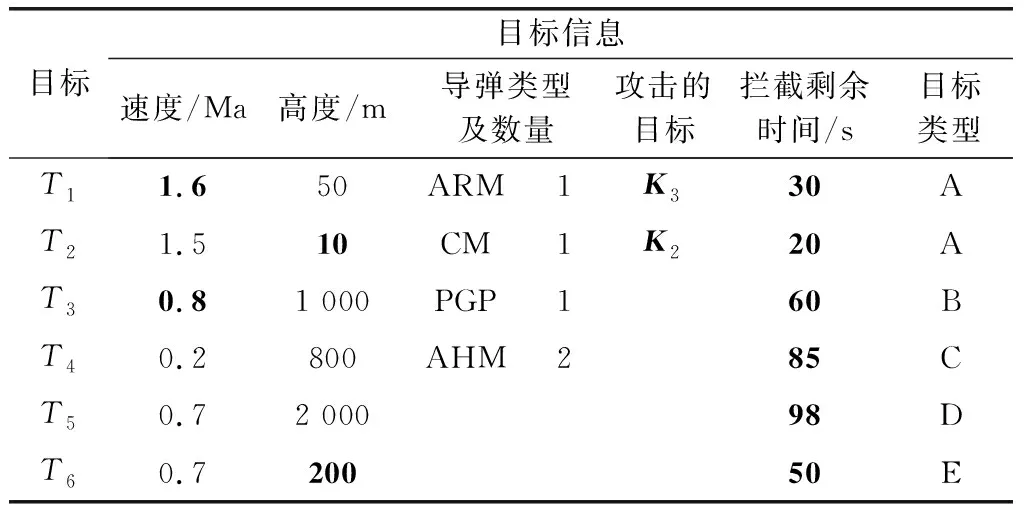
表3 时间片2下各来袭目标信息

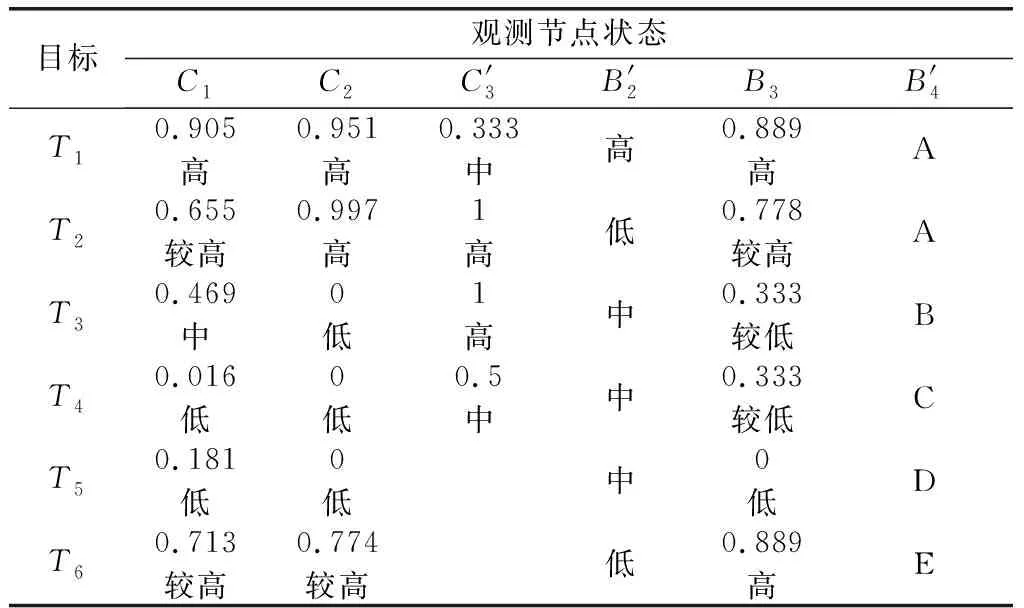
表4 时间片1下各来袭目标观测节点状态

表5 时间片2下各来袭目标观测节点状态

表中,Ti代表第i个目标;ARM代表反辐射导弹;CM代表巡航导弹;PGP代表制导炸弹;AHM代表空舰弹。

注:表中的“空白”表示信息无法判断或缺失,利用前向信息修补算法,可以对其进行修补,得到后验概率。

3.2 仿真分析

利用Netica软件对模型进行仿真推理。

(1)基于BN-Cloud的威胁评估及排序

采用文献[26]中介绍的威胁排序方法即相对熵排序法,对时间片1上的数据进行仿真,仿真结果如图8所示。

图8 时间片1下采用相对熵排序法求解的各目标威胁值对比图Fig.8 Contrast map of target threat value solved by relativeentropy ranking method at time lice 1

从图8可知,来袭目标的威胁顺序为T1>T6>T2>T3>T4>T5。

建立时间片1的BN,网络初始状态如图9所示。

图9 静态BN初始状态Fig.9 Initial state of static BN

根据表4信息进行BN推理,结果如表6所示。

表6 时间片1的威胁评估等级

利用概率-确定度转化和正向云发生器逆运算求解各目标的威胁值,如表7所示。

表7 时间片1下各目标的威胁值

根据表7可知,来袭目标的威胁顺序为T1>T6>T2>T3>T4>T5,其结果与相对熵排序方法的结果相吻合,因此表明基于BN-Cloud模型的排序结果符合实际情况,具有可行性。

利用相对熵排序法对时间片2上的数据进行仿真,其结果如图10所示。

图10 时间片2下采用相对熵排序法求解的各目标威胁值对比图Fig.10 Contrast map of target threat value solved by relativeentropy ranking method at time lice 2

从图10可知,来袭目标的威胁顺序为T2>T1>T3>T6>T4>T5。

由静态BN计算时间片2的威胁评估等级如表8所示。求解各目标的威胁值,如表9所示。

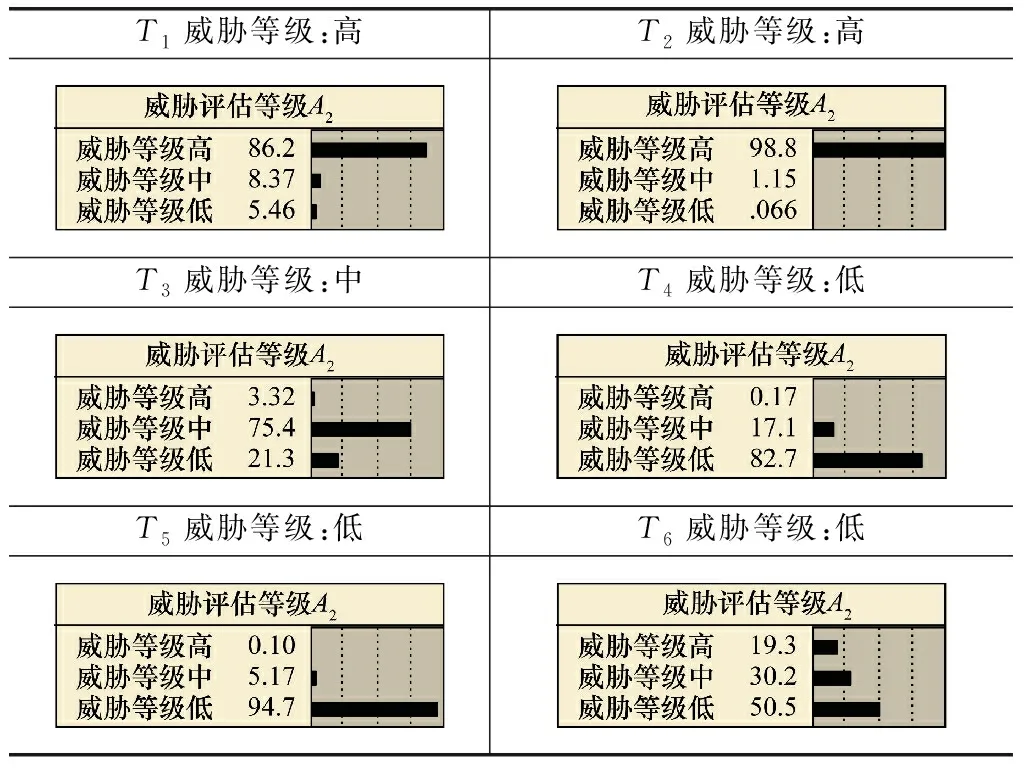
表8 时间片2的威胁评估等级

表9 时间片2下各目标的威胁值

根据表9可知,来袭目标的威胁顺序为T2>T1>T3>T6>T4>T5,其排序结果与相对熵排序法的结果相吻合,进一步验证了所提方法的可行性。

比较BN-Cloud排序法在两个时间片上的威胁度变化情况,如图11所示。

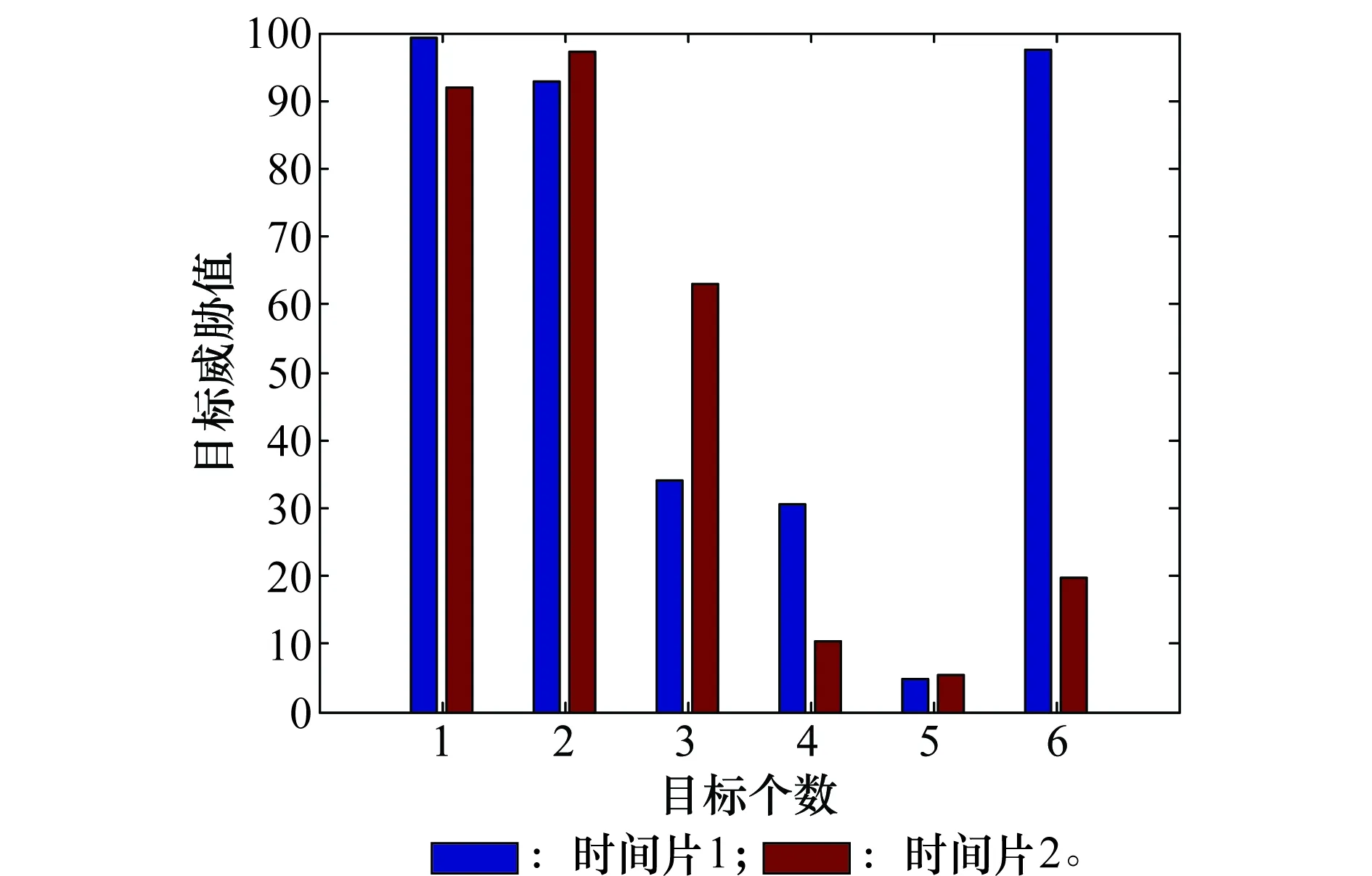
图11 时间片1、2下采用BN-Cloud法求解的各目标威胁值对比图Fig.11 Contrast map of target threat value solved by BN-Cloudmethod at time slice 1 and 2

从图11可见,目标T3和T6在2 s的时间里威胁度发生了较大变化,尤其是T6目标,究其原因是由于观测数据出现了粗大误差,而静态贝叶斯网络鲁棒性较差,从而导致判断误差较大。如图12所示,假设目标接近速度为“高”,目标攻击高度威胁属性为“高”;实际毁伤能力为“高”;攻击意图为“高”;拦截目标剩余时间威胁属性为“高”,这时如果传感器探测目标类型为飞机类目标,而实际目标类型评估指标为C类(飞机类)的概率将不足50%,相对应的A类(导弹类)目标和E类(无法识别类)目标的概率增大,这就需要决策者对目标进行进一步分析确认。由此可见,在威胁评估BN结构中引入可信度后,可以有效辅助决策者进行决策,尽量避免发生决策错误。

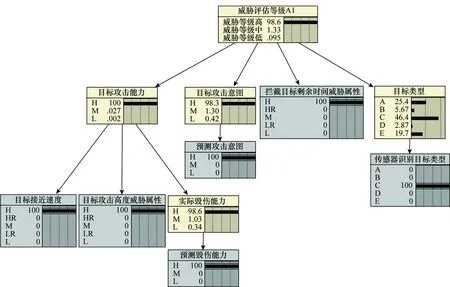
图12 静态BN推理图Fig.12 Inference diagram of static BN

(2)基于DDBN-Cloud的威胁评估及排序

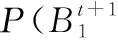
由表11可知,目标威胁排序为T2>T1>T6>T3>T4>T5。

比较两个时间片上各目标的威胁值,如图13所示。

表10 时间片2的威胁评估等级

表11 时间片2下各目标的威胁值

图13 时间片1、2下采用DDBN-Cloud求解的各目标威胁值的对比图Fig.13 Contrast map of target threat value solved by DDBN-Cloudmethod at time slice 1 and 2

4 结 论

针对数据缺失情况下来袭目标威胁评估排序问题,本文提出了基于DDBN-Cloud的威胁评估方法,该方法有效综合了时间序列上的威胁评估数据,对当前时间片的威胁度进行评估和排序,仿真实验结果表明:

(1)本文所提方法能够在数据缺失情况下利用前向信息修补算法进行数据预测修补,通过引入可信度,能够有效地处理观测数据的不确定性,评估结果符合实际情况,准确度较高;

(2)本文所提方法能够有效结合前向时间片上的数据来评估当前时间片的威胁度,并结合正向云发生器的逆运算,有效地将威胁评估概念转化为定量数据,从而进行威胁排序,其评估结果准确度优于BN-Cloud和相对熵排序法,具有一定的容错能力。