二体水下拖曳中的管道振动及水动力分析
张大朋,白 勇,赵望奇,朱克强,姬芬芬,徐显明,荆 彪
1.浙江大学建工学院,浙江杭州 310058
2.宁波大学海运学院,浙江宁波 315211
3.青岛汉缆股份有限公司,山东青岛 266100
4.宁波东方电缆股份有限公司,浙江宁波 315801
随着石油开采逐渐向深海迈进,深海石油开采所需平台和管道的运输和建造也变得日益重要。一般来说,海底管道的铺设和运输方法分为:拖曳式铺管法、卷式铺管法、J型铺管法和S型铺管法。这四种方法各有优缺点[1-9]。
本文重点研究恶劣海况下的拖曳式铺管法。对于一般的拖曳法而言,在恶劣的海况下管道会发生极其不稳定的扰动,这种扰动会使管道发生难以预计的损坏。而Hopkin提出的二体水下拖曳则是一种理想、简便的能够减少拖曳船对水下拖曳管道扰动的措施。目前,国内对该方面的研究尚不多见。
本文将结合水下二体拖曳具体过程对二体拖曳管道进行理论和仿真两个方面的探索,以期对水下二体拖曳管道的工程实践提供一定的指导。二体拖曳是指整个拖曳系统由拖曳绳索、迫沉器、拖曳管道及拖曳船舶构成的管道拖曳系统。
1 海洋环境下的计算理论基础
1.1 水下二体拖曳管道振动分析
当管道在水下进行拖曳时,由于恶劣海况的影响,管道整体将会随波浪进行较大幅度的振动。管道在海中的振动可以近似表示为有阻尼振系在正弦型扰力作用下的振动。

式中:x为管道振动幅值,m;ζ为阻尼比,无量纲;t为具体某一时刻,s;q为衰减振动的圆频率,rad/s;

式中:F为波浪力,N;CD和CM分别为拖曳力系数和惯性力系数,无量纲;ρ为海水密度,取值为1 025 kg/m3;μn为流体速度,m/s;V表示管道体积,m3;A为垂直圆柱的迎流面积,m2。
如果垂直圆柱在波浪中自由摇摆,在Morison方程中必须使用相对速度和相对加速度,这样微分方程可写为:

式中:D为管道外径,m;μ是海流速度,m/s;μa为管道运动速度,m/s;s为管道长度,m。
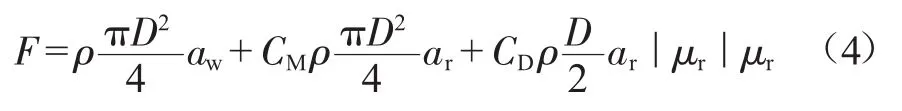
在OrcaFlex中对波浪力的计算正是基于修正后的Morison公式。式(3)即为本文中所采用的扩展型Morison方程,为了方便程序处理,可以将上式变形为:φ为初相角,rad;F0为激扰力的力幅,N;ω为激扰力圆频率,rad/s;k为管道的系数,kg/s2;m为管道的质量,kg;p=k/m,s-2;c为阻尼系数,无量纲。
由振动的基础公式可知,当(k-mω2) +(cω)2接近于0时,将会发生共振现象。由于海况、管道拖曳装置的复杂性和阻尼的影响,该共振现象只会在特殊情况下偶然出现,且持续时间也极为短暂。
1.2 水下二体管道的动力学数值分析
准确描述海洋管道在水下拖曳的情况十分复杂,本文主要参考包含弯曲刚度拖揽的三维动力非线性方程。因本文研究管道拖曳,所以不考虑弹性变形量ε。管道的水动力通过Morison方程的微分形式表示为:
式中:aw为流体惯性坐标系下相对于地面的加速度,m/s2;ar为流体相对于管道的加速度,m/s2;ur为流体相对于管道构件的速度,m/s。
计算出管道水动力后,忽略惯性项,在切向-法向的坐标系中,给出管道拖曳的牛顿运动定律以及动量方程:

为表示管道拖曳过程中的形状和方向对相应的速度分量的影响,给出拖曳管道的运动学方程:

式中:T(s,t) 指在时间t时,与拖曳点距离为s处的张力,kN;Ct为切向阻力系数;Cn为法向阻力系数;θ(s,t)为s处的切向量和x轴正方向之间的方位角度,rad;∂θ/∂S 为管道曲率。Vtr(s,t) 和Vnr(s,t)分别为管道在切向和法线方向上的相对速度,m/s;u(s,t) 和v(s,t) 分别为对应的海流速度,m/s;Vt(s,t) 和 Vn(s,t) 分别为管道的切向绝对速度和法向绝对速度,m/s。
2 二体水下拖曳的数学模型与OrcaFlex软件中的模型建立
2.1 OrcaFlex中的仿真设定
由于拖曳的管道较长,所以选用两艘拖曳船进行拖曳。船长为103 m,型宽为16 m,型深为13.32 m,设计吃水为6.66 m。选用φ275 mm的PE拖缆,单位长度的质量为0.06 t/m。而进行拖曳的管道为APT-5LX65级无缝钢管,外径为0.508 m,内径为0.355 6 m,长度200 m。迫沉器半径为0.5 m,质量可以进行改变。
2.2 OrcaFlex中的模型建立
模型建立后,即可通过改变波高、波浪周期对二体水下拖曳进行多次的模拟试验和计算;也可以改变迫沉器的质量与拖曳管道的长度来获取最佳的拖曳效果。
3 计算结果
设计中主要考虑如下特征条件作为海况条件:水深为100m,浪向取为180°,波高为10m,周期8s。
3.1 在二体水下拖曳中管道的振动分析结果
3.1.1 管道的振动随迫沉器质量变化的情况
图1为在二体水下拖曳中,管道的振动随迫沉器质量变化情况。对比图1(d)~(f)发现,二体水下拖曳的管道在初始点的垂荡值随迫沉器的质量增加而减弱且逐渐稳定,并趋向于振幅为2 m。图1(g)中,管道初始点的垂荡值却大于图1(a)~(c)的垂荡值。本文对迫沉器质量为10~25 t范围进行详细的研究,发现当迫沉器的质量大于10 t时,二体水下拖曳的管道的初始点的垂荡值就随迫沉器的质量增加而变大;而在迫沉器的质量为15 t和18 t时,出现了极其特殊的情况,即管道和迫沉器的垂荡值出现一次极大跳跃,随后又回归于正常。该现象的出现验证了本文在数值分析中所说的共振现象。当迫沉器的质量为 15 t和 18 t时, (k-mω2) +(cω)2为极小值,从而导致垂荡值的突然变大。
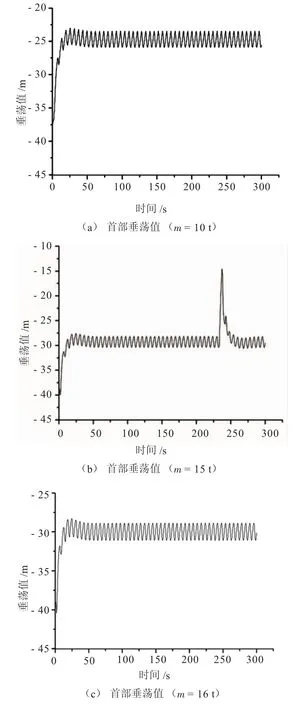
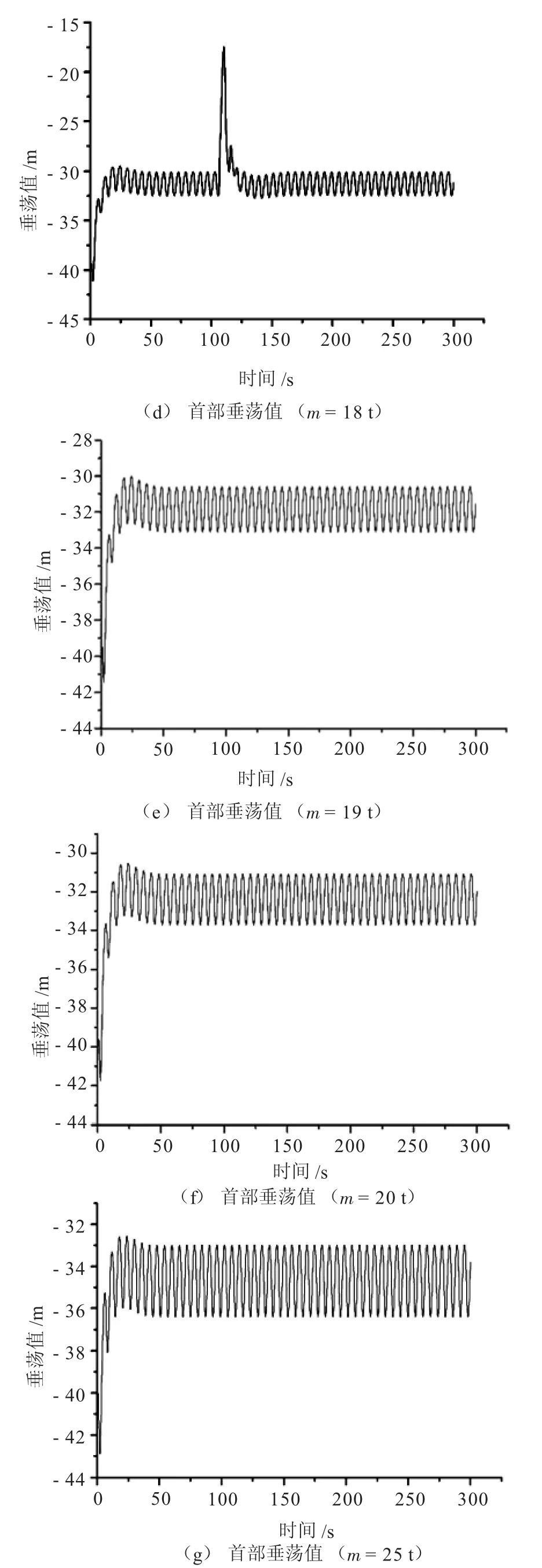
图1 迫沉器质量变化对管道首部垂荡振动的影响
3.1.2 管道在各个长度节点处的振动情况
图2为二体水下拖曳管道在不同长度处的垂荡值,从中可以发现管道首部牵引端的垂荡值约2 m。在距首部牵引端50 m和75 m处,管道的垂荡值最大,达到了3 m;而距管道首部牵引端100、150、200 m处的垂荡值均小于3 m;管道末端的垂荡值甚至达到了1 m左右,远小于最大垂荡值。

图2 水下拖体在距离首部不同节点处的垂荡值
3.1.3 管道的振动随船速变化情况
图3为二体水下拖曳管道在不同拖曳速度下首部牵引端的垂荡值。从图中可以发现随着拖曳速度的增加,水下拖体的拖曳深度逐渐减小,向水平面靠近。对比4种不同的拖曳速度发现,拖曳速度为5 m/s时的垂荡值最小,拖曳速度为3 m/s时垂荡值最大,拖曳速度在7m/s和9m/s时产生的垂荡值在两者之间。
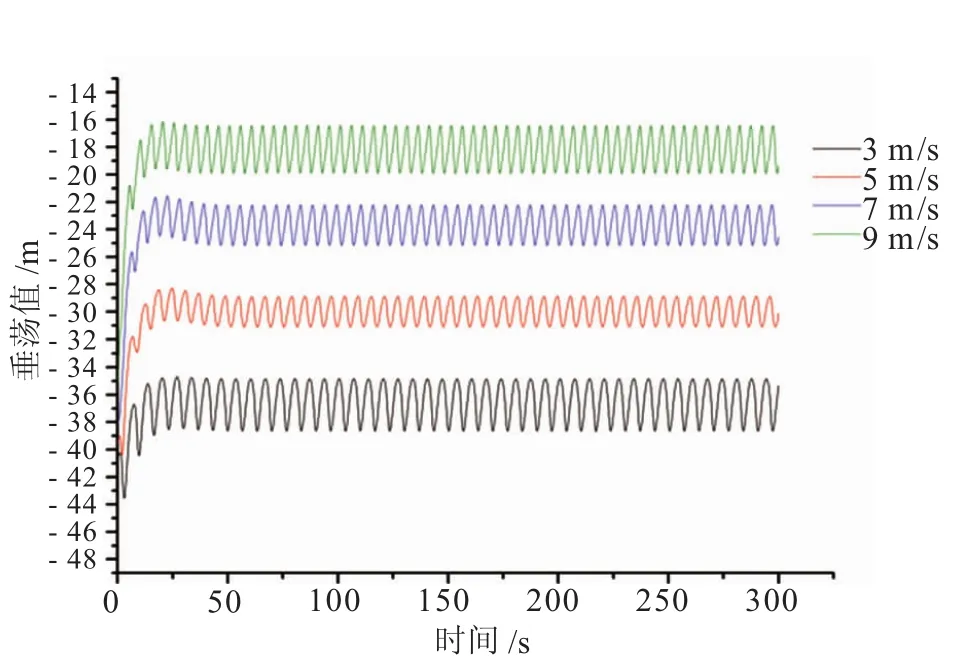
图3 不同拖曳速度下拖体首部垂荡值
3.2 在二体水下拖曳中管道的水动力分析结果
3.2.1 在二体水下拖曳中管道各处剪切力情况
图4为水下拖曳管道各处所受最大剪切力、最小剪切力和平均剪切力的情况。通过观察可以发现管道在首部牵引端和末端内所受的剪切力有两个峰值,且远大于中间的剪切力。而首部牵引端的最大剪切力、最小剪切力和平均剪切力均为最大,最大值为13.53kN,远小于管道能承受的极限剪切力。为保证安全性,在管道与拖揽连接处的强度应加强,以避免剪切力干扰拖曳的进行。

图4 水下拖体各处剪切力
3.2.2 在二体水下拖曳中管道各处有效张力情况
图5为水下拖曳管道各处所受最大有效张力、最小有效张力和平均有效张力的情况。管道首部牵引端的最大有效张力为整根拖曳管道最大有效张力的最大值,达到500 kN,小于该管道设计的最小破断张力(750 kN)。通过观察可以发现管道的最大有效张力和平均有效张力均随管长的增加而变大,而最小有效张力则随管长的增加而减小。

图5 水下拖体各处张力
4 结论
(1)在恶劣海况下(但海流速度较小且稳定时),通过安装迫沉器能够一定程度地减小管道的垂荡值,使其能够进行正常的二体水下拖曳。
(2)并不是随着迫沉器质量的持续增大,其减振效果越好,而是有一定的质量范围。当迫沉器在该范围内,其减振效果将会达到最好,且在该范围内需将迫沉器的质量尽可能减小来缩减拖曳成本,但需避免所选定的迫沉器在拖曳过程中使管道出现垂荡跳跃的现象,从而破坏管道,影响拖曳的正常进行。
(3)管道在拖曳过程中不同节点处的垂荡值,会由于距首部牵引端的距离不同而出现不同的值。垂荡值的最大值一般出现在管道的中前段,而垂荡值最小值出现在拖曳管道的末端。
(4)在水下二体拖曳中,不同的拖曳速度将会对管道的垂荡值产生较大的影响。拖曳速度过小或过大都会导致管道的垂荡值偏大,影响管道的安全性;所以在拖曳之前,需进行水动力分析和振动分析,从而选取适合的拖曳速度。
(5)在水下二体拖曳过程中,管道首部牵引端产生的剪切力、有效张力都是最大值。这就要求在管道连接安装中加固其连接处,以防在拖曳过程中发生严重的变形或者断裂。
(6)通过观察可以发现,管道的最大有效张力和平均有效张力均随管长的增加而变大,而最小有效张力则随管长的增加而减小。
(7)由于拖曳管道的复杂性、OrcaFlex软件自身的限制,以及作者自身水平的局限性,对拖拽管道振动的解释略显粗糙,但对于解决一些实际问题还是有参考价值的。

