强激光场中高次谐波标度律的数值验证

叶会亮,王海跃,刘志勇,苏未安

（江西理工大学理学院，江西 赣州 341000）

0 引 言

原子分子中电子受到强激光场作用时，能够观察到多种非线性现象，阈上电离和高次谐波产生作为其中两种重要的非线性过程受到广泛的研究.高次谐波产生在超快学科领域内有诸多新奇应用，比如光谱分析[1-2]、等离子诊断[3-4]、阿秒脉冲合成[5]以及分子动力学[6-7]等.人们普遍采用一种“三步模型”来描述高次谐波产生过程：首先，原子分子中的束缚电子在强激光的作用下被激发，克服库仑势的吸引而远离母核；然后，电子在激光场的作用下运动而加速；当周期性电场反向时，电子在母核库仑势和电场的共同作用下返回母核，并与母核复合；同时，电子从激光场获得的能量以高次谐波的形式释放.高次谐波谱存在平台结构和截止频率：低阶次的谐波强度急剧下降，随着谐波级次的增加，谐波强度变化趋于平缓，出现一个“平台区”，在平台末端，谐波强度迅速降低，出现一个截止区.

许多研究结果表明了阈上电离和高次谐波中存在标度律，比如，由于中红外波长激光的强场实验中准相位匹配技术较容易实现，并且中红外波长具有增强谐波产生效率的优点，谐波产率和激光波长的标度关系成为了研究的重点[8-9]，许多标度关系得到了建立.比如Tate等[8]认为总的谐波产率与波长的 标 度 关 系 是 λ-（5～6）； 基 于 强 场 近 似 理 论 Pérez-Hernández等[10]发现谐波产率与波长标度关系是 λ-（3～4）；Frolov等[11]指出随着波长增大，谐波产率将以一个很快的速率下降.这些不统一的标度关系很大程度反映出了谐波与波长的关系中包含的物理本质仍未确定.其次，这些研究只局限在谐波产率与波长的标度关系上，并没有考虑到原子结构等因素，因此对其他因素的研究很有必要.

理论研究发现高次谐波谱的主要特征由三个无量纲的物理量确定[12-14]：一是有质动力参数up=Up/ω，即以光子能量为单位的有质动力能量；二是束缚数εb=Eb/ω；三是电离过程中电子吸收的光子数N.当这三个物理量没有改变时，谐波谱的主要特征也不会改变，这就是高次谐波谱的标度律.当激光波长发生变化时，根据标度律选择合适的目标原子和激光强度，就可以得到具有相同特征的谐波谱和物理过程.因而标度律为中红外波长下的高次谐波实验提供了参考工具.

高次谐波标度律是在非微扰量子电动力学框架下推导获得，为了对其进一步验证，一般有两种方法，首先是实验方法，通过使用不同参数的强激光照射不同的原子，然后比较最后的谐波谱结构.但实验方法有其局限性，由于目前实验条件的限制，只能在有限激光强度和波长范围内进行验证.第二种方法就是采用数值模拟的方法，比如基于含时薛定谔方程的数值计算，这种方法的其中一个优点在于能模拟不同的原子和激光条件.

文中基于求解含时薛定谔方程对高次谐波谱进行了数值模拟.通过比较具有不同束缚能量的原子在不同激光参数下产生的高次谐波谱，发现高次谐波谱的主要结构会随着目标原子束缚能和激光波长以及强度的不同呈现不同的变化趋势，但按照标度律的变换，高次谐波谱的基本结构是保持不变的.

1 数值方法

数值求解含时薛定谔方程方法[15]（Time-dependent Schrödinger equation,TDSE）广泛运用在处理强激光与原子分子相互作用过程.通过TDSE方法可以解释许多实验现象以及揭示各种激光与物质相互作用过程.TDSE方法的一个优点是能够模拟实验中难以获得的条件，比如在强场近似中被忽略了的库仑效应.而且TDSE方法经常用于检验理论解析结论的有效性.在模拟中，单电子近似下原子与线偏振激光相互作用的三维含时薛定谔方程表示如下（采用原子单位制）：

其中 A（t）为激光场的矢势，V（r）为库仑势.将波函数采用球谐函数展开，得到：

其中r是电子的位置矢量，r≡r ，Rl（r）是径向波函数，Ω为位置矢量的立体角.当激光场为线偏振时，磁量子系数m被省略了.库仑势采用如下形式：

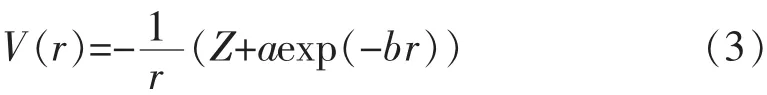
其中Z为原子数，通过调节a和b两个参数，可以获得不同原子的束缚能量.比如a=0（Z=1）对应的是氢原子的基态，而a=9.0，b=2.4569模拟的是束缚能量Eb=15.8 eV的氩原子.在模拟过程中，径向格点数选取3000点，格点间距Δr=0.05a.u.，lmax=60.为了避免激光波形对结果的影响，模拟中采用10个周期的梯形激光，其中上升沿和下降沿分别是0.5个激光周期.

首先采用虚时演化的方法得到目标原子的基态，然后将波函数在加入了激光电场后进行演化，当激光场消失时，得到末态波函数Ψ（tf）.电子偶极距可以写成：

最后对偶极距进行加汉宁窗w（t）的傅里叶变换即可以得高次谐波谱，

2 结果与讨论

标度律指出[13]，束缚能量KEb的原子受到激光频率Kω和强度K3I的激光束的照射产生的高次谐波谱，与束缚能量Eb的原子受到激光频率为ω和强度I的激光束的照射产生的高次谐波谱具有相同的结构，其中K是一个比率因子.

原子中电子的光电离过程受到多个因素的影响，比如原子的束缚能量大小，激光强度和波长等.上述标度关系中谐波谱与束缚能量Eb以及激光频率ω的标度是显而易见的，原子束缚能量增大以后电子仍然必须吸收足够能量的光子才能电离，即光子能量也需变大倍.而谐波谱与激光强度三次方的标度关系才是标度律的核心之处.

在程序中首先将任意波函数在未加入激光电场时进行虚时演化得到原子的初态波函数，目标原子的束缚能量可以通过改变有效势中的参数来控制，然后将初态波函数输入到激光电场下的含时薛定谔方程进行演化，当周期性的激光电场消失时就可以获得末态波函数.最后计算电子的偶极距，通过对偶极距进行傅里叶变换就可以得到高次谐波谱.为了更方便比较，高次谐波谱中的横坐标采用以光子能量为单位的谐波阶次.径向格点间距、激光周期等参数经过了多次调整，计算结果表明谐波谱特征基本不变，从而保证了结果的收敛性.为了验证上述标度律，首先计算并且比较只有一个物理参数发生变化时的谐波谱，从中发现其变化趋势，然后按照标度律变换关系同时改变这三个物理参数，观察谐波谱的变化情况.

当只有束缚能量变化时谐波谱的变化情况如图 1 所示，图 1 中分别是 Ne 原子（Eb＝21．5 eV）和束缚能Eb=10．75 eV的模型原子在波长800 nm和激光强度1.0×1014W/cm2的强激光照射下的谐波谱.结果显示两个谐波谱都呈现平台结构和截止区结构，并且平台的宽度都大致是相等的.根据半经典理论的计算结果，谐波截止能量为Ecutoff=Eb+3.2 Up.考虑到有质动力能量Up是相同的，因此这两个谐波谱截止阶数应该大致是相同的，从图中也可以看出两个谐波谱已经在截止区（第29阶）开始重合，这说明计算结果与理论分析是一致的.Ne原子在平台区的谐波产率普遍都比模型原子要低至少两个数量级.这是因为原子核对电子的束缚越大，电子电离的几率自然要小一些.结果表明了束缚能量的变化主要影响的是谐波的产率.

图1 不同束缚能量原子的高次谐波谱

图2 表示了Ne原子在激光强度相同 （I=1.0×1014W/cm2）而波长发生变化时的谐波谱.两个谐波谱最显著的区别就是平台区的宽度.由900 nm波长激光产生的谐波谱比波长600 nm的情况具有更宽的平台.这也是实验上经常使用红外激光脉冲获取超短脉冲的原因，平台越宽，合成的激光脉冲的持续时间就可以越短.这是由于有质动力能量与波长是二次方的关系，因而电子可以从较长波长的激光场获取更大的能量.并且，从图中可以发现低阶次（第15阶以前）谐波的产率是大致相等的，这说明波长的变化实际上主要是影响了平台宽度，对谐波产率的影响相对比较小.

图2 Ne原子在不同波长的激光脉冲照射下的高次谐波谱

图3 表示了在波长800 nm而强度不同的激光作用下Ne原子的高次谐波谱，对于激光强度I=1.0×1014W/cm2，谐波谱平台展宽至第29阶次，而对于激光强度为3I时，平台区宽度达到了第57阶次，并且平台区的谐波产率也普遍要高两个数量级以上.这说明了激光强度对谐波谱结构具有多方面的显著影响，也体现了激光强度大小在谐波生成过程中的重要性.

综合上述比较的结果可以发现，束缚能Eb、波长λ和激光强度I从不同方面影响了高次谐波谱.增大λ或I将对谐波平台区进行展宽，而增大I或减小Eb将增大谐波产率，因此如果以一定方式增大I和Eb并且减小λ，谐波谱的结构就可能保持不变，标度律就提供了这样一种变换方式.

图3 Ne原子在不同强度的激光脉冲照射下的高次谐波谱

对于不同束缚能量Eb的原子，如果束缚能量相差K倍，为了使谐波谱特征保持不变，可以将激光频率变为K倍，而激光强度应该变为K3倍，这就是标度律变换关系.这本质上是要保证有质动力参数 up=Up/ħω∞I/ω3不变.Xe原子和 Ar原子之间束缚能量相差1.3倍，为了验证标度律，模拟中采用了这两种原子.Xe原子和Ar原子在不同波长和不同激光强度下的高次谐波谱如图4所示.其中 Xe （原始谱）：Eb=12.13 eV，λ=1064 nm，I=3.0×1014W/cm2，Ar （变换谱）：Eb=15.76 eV，λ=818 nm，I=6.6×1014W/cm2.标度变换比率K=1.3.从图中可以发现，谐波能量和产率、平台宽度以及截止区等谐波谱结构都是一致的.这说明了按照标度变换后谐波谱是能够保持不变的.从而标度律得到了验证.在模拟中，还比较了原始谱和将Ar原子情况中的激光强度分别变成K、K2和K4倍后的谐波谱，发现二者的平台宽度和谐波产率存在很大的不一致.这体现了标度律中激光强度三次方关系的核心作用，其本质是要保证有质动力参数保持不变.

3结 论

通过数值求解含时薛定谔方程，计算了不同原子在受到各种强激光场作用下的高次谐波谱.揭示了原子束缚能量、波长以及激光强度对谐波产率的影响表现在不同的方面.而高次谐波谱的结构在标度律变换下是保持不变的，这反映了在标度变换下光电子电离以及与母核复合等过程的内在物理本质是一致的.这为高次谐波在探测原子结构、合成超短脉冲等方面的一些应用提供了参考工具.