改进型LSTM变形预测模型研究

许宁， 徐昌荣

（江西理工大学建筑与测绘工程学院，江西 赣州341000）

0 引 言

随着人类社会的进步和国民经济的发展，当代工程建设进程大幅度加快，对当代工程的形状、范围、尺度等有了更严格的要求.在工程的施工和运营阶段，工程会由于各种主观和客观因素的影响而发生形变，变形量一旦超过承受允许值就会产生损伤甚至会引起重大灾害，给人民生命和财产造成巨大损失.因此，必须建立高精度预测模型，结合已测数据对形变体实时做出变形状况的预测[1].变形预测常用的模型有回归分析、灰色理论、时间序列分析和BP神经网络等，但这些模型均有一定的局限性.仲洁[2]分析了常用预测模型的局限性，并建立了时间序列—BP神经网络的变形预测模型.周永胜等[3]针对传统预测模型结构单一、预测精度不稳定等问题，提出了多元体系的组合预测模型，得到了比传统单一模型更好的结果.然而组合预测模型的构建过程复杂、人工依赖性强，不利于在实际中推广和使用.

近年来，随着深度学习的迅速发展，部分深度学习模型逐渐被应用于时序数据的研究中.深度学习模型是由多种非线性映射层构成的深度神经网络，能够对输入信息逐层提取特征，找出其深层次的潜在规律[4].在深度学习众多模型中，LSTM是用来处理长时间序列数据的模型之一，已在多个领域有所应用.王鑫等[5]基于LSTM模型利用机器历史故障数据预测机器未来健康状况.Li等[6]利用长短时记忆网络（LSTM）自动提取历史空气污染物数据中固有的有用特征.陈亮等[7]应用深度学习框架搭建改进的LSTM模型成功预测某省电力公司短期内电力负荷.Zhang等[8]采用长期短时记忆（LSTM）预测海面温度（SST），并做出短期预测（包括一天和三天）和长期预测（包括每周平均和月平均）.朱乔木等[9]提出了一种基于LSTM的多变量风电场超短期功率预测方法，同人工神经网络和支持向量机对比精度更高.尽管LSTM在多个领域的时序数据处理方面有了较多成果，但在变形预测方面未发现相关研究.

文中基于LSTM在时序数据处理方面的优势，将其应用于变形预测.研究发现LSTM网络深度受有限变形序列数据的影响较大，直接影响到整个模型学习和预测能力.针对LSTM网络深度受有限时序数据影响这一问题，基于有限变形时序数据，提出一种可适量增加LSTM网络深度的改进模型.旨在减少LSTM网络模型受变形有限序列的影响，提高模型对输入信息的特征提取效率，进而提高整个模型的学习和预测能力.

1 LSTM模型概述

递归神经网络（RNN）是一种深度神经网络，可以在时间序列可变环境下进行分类和生成任务，在图像识别、语音辨识、文字识别领域有很大应用[10-14].RNN最大的优势在于将时序概念引入神经网络，能够做到上一时刻输入的数据对当前时刻数据产生直接的影响.具有足够隐藏层数目的RNN能够以任意精度逼近需要预测的序列，其关键在于RNN独特的“递归连接[15]”能够在网络中保留先前输入的信息，进而影响RNN网络输出.随着时间序列长度增长，RNN无可避免地出现梯度爆炸和梯度消失问题[16].于是，Hochreiter和Schmidhuber[17]提出了LSTM模型，该模型不仅有效地避免了梯度消失等问题，且提高了处理时间序列中间隔或延迟较长的事物的能力.

LSTM是建立在RNN基础上的一种深度神经网络[18]，其核心是加入了特殊的单元（记忆模块）对当前信息学习并提取数据之间相关联的信息和规律，以此进行信息传递.由于具有特殊的单元，使得LSTM可以获得更持久的记忆能力，更容易解决RNN中梯度爆炸和梯度消失问题.LSTM凭借记忆模块减缓信息丢失速度，更加适合深度神经网络计算.每个记忆模块共有三个“门”结构，分别为输入门（it）、忘记门（ft）、输出门（Ot），用来选择性记忆反馈的误差函数随梯度下降的修正参数，具体结构如图1.

图1 LSTM记忆结构

LSTM记忆模块的具体工作原理如下：

图1中，LSTM有两条随时间传递的状态链h（隐藏层状态）和C（单元状态），RNN只有单元状态C是随时间传递的.ht-1是上一时刻隐藏层传入当前时刻的值，Xt为当前时刻输入值，Ct-1是上一时刻LSTM记忆单元状态值，Ct是当前时刻的LSTM记忆单元状态值.ht-1和Xt在经过忘记门时通过计算得出需要丢弃的信息，由计算得到输出到单元状态的值在0和1之间，0表示全部忘记，1表示保留全部信息.见公式（1）：

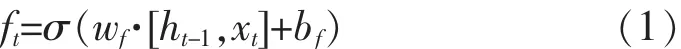
式（1）中：w和b分别是忘记门里的权重矩阵和偏置向量，σ是激活函数Sigmoid.Sigmoid是一种将变量映射到[0,1]的S型生长函数，具体公式

新信息更新到单元中，共有两个过程.先是经过有Sigmoid函数的输入门计算出需要更新的信息（公式2），再由tanh层创建一个新的值kt加入到单元状态中（公式3）.

公式（2）和公式（3）得出的结果相乘并和上一时刻单元状态值经忘记门得出的结果相加得到当前时刻单元状态值，如下：

最终输出结果取决于单元状态.首先Sigmoid对输出结果分类，选择需要输出的数据，用tanh函数对单元状态进行处理，得到隐藏层传递给下一时刻的状态值ht，ht经过Sigmoid处理后可得到当前时刻预输出值 y，见公式（5）～公式（7）.

2 LSTM模型改进

2.1 LSTM改进原理

LSTM模型训练的实质是每层网络层的神经元依次提取输入信息的特征，信息提取在于训练参数（权重等）的调节.LSTM网络层越深，参数调节自由度越高，提取的特征越全面.LSTM模型的网络深度由记忆模块数决定，单个LSTM记忆模块含有一层隐藏层.记忆模块由输入数据序列长度决定，输入数据序列长度是由实际数据在训练过程中分割数据采用的分割尺度而定.在有限的变形序列样本中，分割尺度不宜过大，致使LSTM记忆模块的选择有限，导致网络模型深度不够，影响预测精度.基于LSTM的此类问题，在LSTM模型前加入多层神经网络，给予同LSTM一样的初始权重，不仅有效地增加了整个模型深度，提高了训练参数调节自由度，还能够预先对输入信息进行部分特征提取，提高整个网络模型的特征提取效率.网络层数增加不可盲目，层数过深可能造成训练过拟合.改进模型的序列分割尺度和增加的神经网络层数由多网络搜索方法得出结果分别为10和5（网络搜索方法见2.2.3）.

具体结构如图2，神经网络层和LSTM模型的衔接应用全连接层（Dense）[19]，主要作用是将学到的特征完全传递到LSTM中.整个改进模型输出层也采用Dense，目的是模型回归.整个模型还嵌入了随机丢弃层 （Dropout）[20]，Dropout的作用是随机抽取模型中一定概率 （本模型设置概率为0.2）的神经元权重不参与训练，可有效减少过拟合现象的发生.

2.2 模型预测步骤

改进LSTM模型的预测主要分为两个过程.第一部分是模型的训练过程，找到使模型达到最大收敛效果的参数；第二部分是预测过程，通过模型训练得到的参数直接求得预测结果.

2.2.1 模型训练

改进LSTM模型训练过程采用时域后向传播（Back-Propagation Through Time，BPTT）算法[21]，即先将LSTM按照时间顺序展开为一个深层的网络，然后使用经典的误差反向传播（Back Propagation，BP）算法对展开后的网络进行训练.和BP算法一样，BPTT也需要反复应用链式规则.

图2 改进的LSTM模型结构

网络训练主要以隐藏层为研究对象.主要训练过程有：

1）在输入数据到改进模型之前，将变形序列数据 D＝[d1，d2，…，dn]分割成训练集 ttr＝[d1，d2，…，dm]和测试集 tte＝[dm+1，dm+2，…，dn]，满足约束条件 m＜n.

2）训练集数据归一化.输入至改进模型的序列要进行归一化处理，归一化的作用是将所有数据映射到[-1,1]区间，可保证模型收敛加快，其次可方便后期数据处理.归一化公式如下：

式（8）中：x为训练集样本数据，xmin为训练集样本最小值，xmax为训练集样本最大值，y为归一化后的训练样本数据.

3）训练参数调节.参数调节包括网络内部调节和网络外部调节.内部调节为各网络层的权重调节，由BPTT算法以及优化算法进行修正；外部调节为参数的选择，包括分割尺度、训练迭代步数和学习率选择等，可由网格搜索方法进行选择 （见2.2.3）.如图 2，[X1，X2，…，Xn]是需要输入的变量，假定输入单个变量X，X归一化的训练集按分割尺度分为多个序列长度均为 10的序列[x1，x2，…，xn]，逐个序列依次传入模型输入层.输入序列先在LSTM前置神经网络中处理后由全连接层输出，该序列[y1，y2，…，yn]依次传入 LSTM 记忆模块中，最终输出序列Y.序列Y的误差检验由损失函数控制，当损失值过大时，模型会通过BPTT算法和自适应矩估计[22]（Adaptive Moment Estimation，Adam）随机梯度优化算法不断修正各网络层权重，进而得到训练最优的隐藏层.损失函数包括误差函数和最小误差函数两部分.误差函数计算公式如下：

其次是最小误差函数即损失函数：

式（10）中：N为样本个数.训练结束后损失函数计算的实际值相当于均方误差（MSE），可用于预测精度评定.

2.2.2 模型预测

模型预测是应用训练好的改进LSTM模型进行预测.预测采用迭代的方法.

1）首先，当训练集最后一个序列 ttr-1=[dm-9，dm-8，…，dm]输入训练好的模型时，可得到预测值为yt1=[ym-8，ym-7，…，ym，ym+1]，对应时间为 m+1 时刻的预测值.然后将ym+1和ttr-1序列后9个数据合并成新的序列为 ttr-2=[dm-8，dm-7，…，dm，ym+1]，将 ttr-2输入至训练好的模型中，可得到m+2时刻的预测值ym+2，以此类推，可预测出和测试集序列相对应的预测值序列yt=[ym，ym+1，…，yn].

2）预测值序列yt反归一化处理.由归一化公式可得反归一化公式如下：

式（11）中：x为训练集样本数据，xmin为原训练集样本最小值，xmax为原训练集样本最大值，y为预测序列，x为反归一化预测值.

3）检验预测误差.用同样的方法预测出训练拟合序列 ytr=[y1，y2，… ，ym]， 计 算 ttr和 ytr，以 及 tte和yt的偏差，定量地给出模型的拟合精度和预测精度.

2.2.3 参数优选

在构建上述预测模型时，涉及到众多参数的选择，其中主要有序列分割尺度l，加入的神经网络层数n，以及学习率η.文中采用基于多层网格搜索的参数优选方法，该方法是一种简单实用，可并行计算的实用方法，很好地满足变形预测的精度要求.参数优选的依据是测试集上所有数据的预测精度最高，即预测误差达到最小.目标函数可以表示为如下公式：

满足：

其中，stepl、stepn和 stepη分别表示对应参数搜索的网格步长.l、n和η构成一个三位搜索空间，可以通过网格搜索的方法获取最优值.搜索过程主要包括3层，由内到外为 l、n和η.首先固定随机种子数seed和训练步数steps（为减少训练时间，训练步数设置较小），根据公式（13）～（15）预设 3 个参数的取值范围（为了降低模型搜索复杂度，和控制在较小范围去取值，η从1开始）.然后，遍历3个参数的取值范围，训练并预测改进LSTM模型，保存对应的改进模型预测精度和参数，取精度最优的模型所对应的参数.

2.3 多点预测模型

现大多数工程项目在施工期间均会进行实时监测，并对后期工程施工过程中的某些变形结构做出合理预测.一般来讲，应用前期监测数据的不断更新，实时对后期工程进行变形预测是保证工程安全运营的重要方法.目前大多数工程项目具有的特点是：施工期紧、工作量大、影响因素多以及监测项目多等，因而迫切需求高效率的变形预测模型，来高效率的保证工程项目的安全施工.

LSTM同大多数神经网络类似，具有多变量建模功能，即支持多变量的输入和多变量的输出.LSTM能够做到不同点之间的序列数据在训练和预测过程中不产生任何交集，可防止时序数据在预测过程中出现不可控因素.前文提到的LSTM模型预测步骤是基于单点预测展开叙述的，实际过程中需要用到多变量预测（即多点预测），LSTM多点预测模型原理和单点预测模型的训练及预测过程完全一致，都包含模型训练、预测和参数优选等步骤，且各过程应用的方法一样，其不同之处在于时序数据的构造.多点预测模型需根据输入、输出序列和点个数存在的关系进行序列维数选定，通常一点对应一个维度，如：单点预测训练集序列为ttr=[d1，d2，…，dm]，多点预测模型训练集序列构造为同样地，多点预测模型在训练和预测过程中序列维度均与输入序列维度一致.LSTM的优势不仅仅是对时序数据提取的特征信息进行长短期的记忆，还会对修正后的权值进行记忆和共享，即LSTM模型的正反向传播过程都有状态的记忆.这一优势能够帮助LSTM模型在多点预测过程中节省一部分权值修正耗费的时间，对于工程项目在施工过程中的变形预测具有一定适用性.

3 工程应用实例

我国西南部某开采矿区发生严重的沉降和位移，为保证矿区工人及建筑物的安全，对变形区进行全天候的自动监测.实验数据来源是该矿区的监测点观测数据，根据实验需要选择一个点的沉降数据（H1）和 3 个点的位移数据（L1，L2，L3）.

对比实验分为两个：

实验一：LSTM模型和改进的LSTM模型对比实验.均使用点H1的540期数据训练，120期用来评估测试.两种模型预测结果如图3.

图3中实心圆形代表改进的LSTM模型的预测值，星形代表LSTM模型预测值，实线代表真实值，明显的看出LSTM和改进的LSTM模型的预测值和真实值之间的差值均比较小，且改进后的LSTM总体预测误差更小.从图3直观反映出预测结果存在一定周期性，且周期与经参数优选后的分割序列尺度一致.由于LSTM模型是根据时序数据进行预测，且采用滚动预测方法，当某个预测序列最后一个值输出后，此时间段预测结束，再进行下一时间段的预测，所以分割尺度的选定可能造成预测结果呈现周期性变化.

从120期数据中随机取出11期数据对LSTM两种模型预测结果如表1.

通过分析表1和图3可以得出LSTM模型和改进的LSTM模型都有较强的预测分析能力和拟合能力，预测值与真实值之间产生的残差值较小.改进的LSTM具备了LSTM在时序数据预测上的能力，且有效地提高了预测精度.由此可以得出改进的LSTM在变形数据预测方面具有良好的实用价值，预测数据较LSTM更精确、更有效.

为进一步比较改进的LSTM模型和LSTM模型预测能力，采用标准差对残差值进行离散度检验.

其中，n为样本个数，Xi为第i个样本残差值，为样本残差平均值.

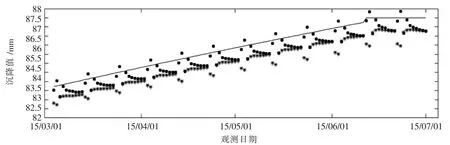
图3 LSTM和改进的LSTM模型预测结果

表1 LSTM模型和改进的LSTM模型预测结果

由公式 （16）和公式 （17）计算得到改进的LSTM模型预测值剩余标准差为0.2082 mm，LSTM模型预测值剩余标准差为0.2306mm，所以改进的LSTM模型预测误差离散度比LSTM模型更小.综合评定，改进的LSTM模型更优.

实验二：单点预测和多点预测对比实验.应用改进的LSTM模型对L1，L2，L3分别进行单点预测和多点预测.训练数据为540期，测试数据120.

以L2为例，单点预测结果和多点预测结果分别见图4、图5.

为进一步对比多点预测和单点预测的预测效果，采用的评价指标有平均值、最大残差值、标准差、预测时间，对所有的预测结果残差值进行统计分析，结果见表2.

图4 改进的LSTM模型单点预测结果

图5 改进的LSTM模型多点预测结果

表2 单点和多点预测结果

结合图4、图5和表2可知，多点预测和单点预测结果不一致.总体上多点预测精度不低于单点预测，且残差值的标准差更小，说明多点预测效果不因输入变量数的多少而降低预测精度.多点预测时间为583 s，单点预测总时间为1452 s，多点预测大大缩短了预测时间.总之，改进的LSTM模型适用于多点预测，在不损失预测精度的前提下，能减少预测所需时间.

结合实验一和实验二可知，LSTM以及改进的LSTM基于自身的高度自学习性和处理时序数据的优势，变形数据预测精度均较高，且改进的LSTM在变形预测中的能力优于LSTM.当需要预测的监测点较多时，改进的LSTM可在保证预测精度的前提下，进行多监测点序列数据同时预测，可减少预测时间.因此，改进的LSTM模型在变形预测中具有良好的应用价值.

4 结 论

文中基于西南部某开采矿区部分沉降和位移数据，选取主要研究时段为矿区变形前后，应用LSTM模型和改进型LSTM模型对变形数据进行处理与分析.得出以下几点结论：

1）LSTM模型应用于沉降数据的预测，预测误差大部分在1mm以下，预测精度较好.

2）改进的LSTM模型有效改善LSTM在有限的变形数据预测中存在的问题，相比较LSTM更能高效地提取时序数据之间的相关性和规律性，使得改进的LSTM预测能力更强.

3）改进的LSTM适用于多点预测.进行单点和多点预测对比试验发现，改进的LSTM在同时处理多点数据的过程中，并不会降低预测精度，对比单点预测反而能减少预测时间.

4）虽然改进的LSTM对比LSTM在精度上有所提高，但该模型牺牲了时间为代价.改进的LSTM在LSTM上增加了多层神经网络，延长了数据训练时间.为改善此类问题，应将原始数据进行编码处理，减少数据读取时间；模型训练过程中也应选择更优地网络优化算法，减少训练迭代次数.

5）从实例中可以发现，沉降量的预测结果呈现出周期和分割尺度一致的周期性，而位移变形量预测值未出现周期性.此问题仍需进行多种实验研究，来判断预测结果周期性变化是否与数据类型、非线性程度以及分割尺度等其他因素相关.