一种改进的K-means算法

尹宝勇， 吴斌， 刘建生

（江西理工大学理学院，江西 赣州341000）

0 引 言

伴随着数字化时代的高速发展，数据挖掘技术已成为当前研究的热点之一.而聚类分析作为现今数据挖掘中最为流行的一种技术，已被广泛的应用于图像分割[1]、模式识别[2]、病毒入侵检测等领域中[3].根据不同领域的应用，人们研究出了不同的聚类算法，其中主要分为基于网格、基于密度、基于层次以及基于划分的聚类算法.其中以基于划分的聚类算法更为被人们所常用.而K-means作为基于划分的算法中最经典的一个聚类算法，被广泛的应用于各领域中[4-6].并且K-means算法因其高效的执行效率[7]，备受研究人员的青睐.然而该算法也存在如下的缺点[8]：①传统K-means算法需事先预知聚类中心的数目；②传统K-means算法采用欧式距离作为样本划分的准则，仅能体现对象间的相似性，样本对象间相关性不能得到很好体现.为克服传统K-means算法聚类中心数目难以确定的问题，大量改进的K-means算法已被提出.Jing等[9]重新定义内类距离与内间距离的关系来提高自动划分聚类中心数目的准确度.文献[10]及文献[11]中主要采用了BWP指标对聚类效果进行评价.谢娟英等[12]提出了一种新的统计计量指标Fr，通过采用该指标对类别数目的优劣进行评价.

除了以上几种改进算法以外，K-means算法也常与其他智能算法相结合使用[13-14].文中在分析已有改进算法的基础上，提出一种改进的K-means算法用于实现聚类中心数目的确定以及增强样本对象间的相关性.

1 K-means算法回顾

K-means算法是一种采用交替最小化方法求解非凸优化问题的算法.它是将一个给定的数据集划分为用户指定的k个聚簇，有着较高的执行效率.在历史上，有着许多不同领域的研究人员都对基本的K-means算法进行了研究，其中比较知名的有 Forgey（1965），McQueen（1967）等[15].Jain 与Dubes详细的描述了K-means算法的发展历史和多种变体.其算法步骤如下[16].

算法输入：数据集X，聚类数k

算法输出：聚类代表集合C

Step1：从整个数据集X中，随机任意选取k个样本对象作为初始簇中心；

Step2：计算数据集中每个样本对象xm到簇中心ci的距离；

Step3：找到每个样本对象xm到簇中心ci的最小距离，并将该样本对象xm归为与ci相同的簇中；

Step4：计算同一簇中对象的均值，更新簇中心；

Step5：重复 Step2～Step4，直到簇中心不再发生改变.

K-means算法具有简单、易于实现等优点，但同时K-means算法确定聚类数目是困难的.图1显示相同数据集在不同聚类中心数下的实验结果，从图1中可看到准确的聚类数对于聚类准确率的影响是非常大的.

2 CS-kmeans算法

在分析已有改进K-means算法的基础上，本文针对传统K-means算法中不能自动确定聚类数目、对象间相关性难以体现的缺点，提出了一种改进的CS-kmeans算法.CS-kmeans算法的改进有：①样本间距离的计算过程中引入了样本相关性，为欧式距离添加相关性缩放因子；②将最大类内距离与最小类间距离作为样本划分或合并的标准.具有相关性缩放因子的距离定义如下：

图1 同聚类中心数k时的聚类结果

其中，d（xi，xj）表示 xi和 xj的欧式距离，cor（xi，xj）表示 xi与 xj的皮尔逊相关系数，Max_cor，Min_cor分别表示样本对象间皮尔逊相关系数的最大与最小值，g（xi，xj）表示归一化后的相关系数，0.001 为了防止 g（xi，xj）为 1 时样本间距离为 0.

最小类间距离：

最大类内距离：

其中，xi是以cj为聚类中心的对象.

平均类间距离：

其中，k为聚类数，ci和cj代表簇中心.

因为最小类间距离小于等于平均类间距离，最小类间距离越大，类与类之间的差异性越明显，则聚类效果越好，所以选用当前划分的平均类间距离来近似理想划分的最小类间距离，即.最大类内距离越小，类中对象相似性越强，聚类效果越好，因此理想划分下的最大类内距离不妨为 0，即=0.

另一方面，在聚类过程中，随着类别数的增多，类与类之间将变得越来越密集，假设此时对于相邻的两类之间边界样本间距趋近于0时.此时存在a3+a4≥a5，其中 a3、a4为内类距离，a5为类间距离.而聚类过程中，最大的内类距离应尽可能小，既相邻两类间内类距离之差应尽可能小，不妨建立a3=a4=0.5×a5，可得 Inter=2×Intra，既 a1=2×a2.关系示意图如图2所示.

图2 类内与类间距离示意

将 a1=2×a2代入公式（5），可得：

算法输入：包含n对对象的数据集X，X={xm|m=1，2，…，n}，初始聚类中心数目 k0，点密度领域半径λ；

算法输出：聚类代表集合 C，C={ci|1，2，…，k}；

Step1：初始化k=k0，按文献[9]初始化方法选取k0个密度高的样本为初始簇中心ci；

Step2：按传统K-means算法流程聚类，计算平均类间距离d；

3 实验仿真与分析

为验证文中算法的有效性及合理性.文中选用6组UCI数据集与4组人工模拟数据集在相同环境将文中算法、传统K-menas算法、文献[9]算法（Rt-kmeans）、文献[10]算法（BWP）及文献[11]算法（MST_Fr）在聚类准确率、标准差、收敛时间、k值搜索上界、聚类中心数目5方面进行对比.数据集如表1所示.

文中验证过程分为两步.第一步是通过选取不同初始聚类中心数目k时，对算法确定类别数目的鲁棒性及准确性进行分析，如表2所示.第二是对文中所选的五个评价指标进行实验对比，实验中的聚类准确率，收敛时间是通过10次单独实验取平均值进行记录，实验结果如表3、表4所示.

表1 实验数据集

表2 不同k值时各数据集CS-kmeans算法下的聚类中心数

表3 UCI数据集实验结果

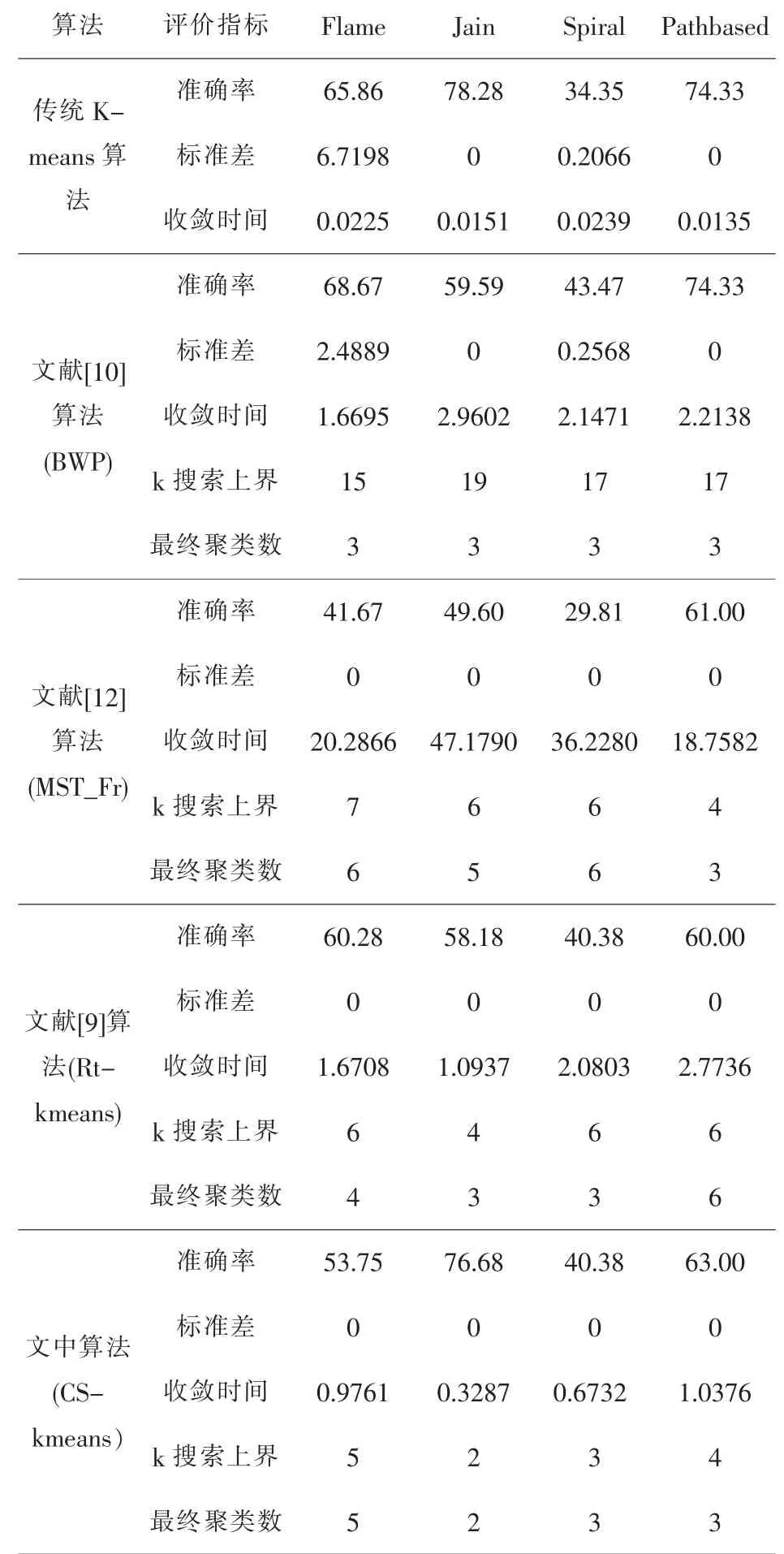
表4 人工模拟数据集实验结果

由表2可知，当选取不同的初始聚类中心数目k时，除了Yeast与Jain数据集，CS-kmeans算法对文中其它8组数据集均能获得稳定的聚类中心数目.虽然Yeast与Jain数据集所得结果不稳定，但不同结果之间的差值也较小.并且对于文中所选用的大部分数据集，最终所确定的聚类中心数目与标准聚类中心数目也比较一致.

从表3与表4可以看出，对文中所选用的10组数据集传统K-means算法虽然收敛速度快，但仅少数数据集能获得较好的聚类效果，大部分数据集所得聚类结果均不稳定，并且传统K-means算法需要提前输入准确的聚类中心数目.文献 [10]算法、Rt-kmeans算法、MST_Fr算法虽然自动对聚类中心数目进行划分，但文献[10]算法需要较大范围的对不同的k值进行搜索，同时从各数据集最终所得聚类数可看出，该评价指标仅对类别数目为3的数据集才能获得较好的聚类效果，并收敛速度也较慢.MST_Fr算法虽然能对不同类别数的数据集进行划分，但是最终所得结果与标准聚类中心数目差别较大，聚类准确度较低，并且该算法在计算各样本点密度及更新簇中心过程中耗时较长.Rtkmeans算法虽然收敛速度也较快，但该算法对于确定聚类中心数目的准确度以及聚类结果的准确率仍存在明显不足，并且从Yeast数据集的聚类结果看出，当数据集类别数较多时，文献[9]与[10]中的算法所得的最终聚类中心数的结果是较差的，虽文中算法也没有得到标准聚类数，但分析Yeast数据集发现，Yeast数据集样本分布是不均匀的，由表1得Yeast数据集后四类样本数仅为总样本数的7%，所以CS-kmeans算法所得结果比较可靠.

相比其它4个算法，CS-kmeans算法无论从聚类结果准确率、确定聚类中心数目及收敛速度等方面都能获得较为优越的聚类结果.通过上述实验结果表明，文中算法能够有效的提升聚类的效果.

4 结 论

文中通过使得最小类间距离及最大类内距离与理想最小类间距离与理想最大类内距离尽可能接近来确定聚类数目，使用类间距离与类内距离之间的关系实现对样本对象的自动划分与合并.并且与传统的K-means算法以及其他几种改进的K-means算法相比较，文中提出的算法在聚类准确率、稳定性、收敛时间等方面都能得到更好效果.