向量优化的高阶微分条件
唐琦林, 廖永志, 胡 敏
(攀枝花学院数学与计算机学院,四川攀枝花617000)
向量优化问题在经济理论及工程技术等领域中有着广泛的应用.例如最早研究的Pareto有效解和弱Pareto有效解[1-10],最近研究的Sharp解和弱Sharp解等[8-11].利用广义导数,获得了这些解的一些充分或必要的最优性条件[10-13],这在数学规划的很多问题当中都起着关键的作用,比如灵敏度分析、误差界分析等方面.文献[14]把泰勒公式扩展到Ck,1函数,应用它得到高阶拟凸函数的最优性条件.本文主要研究2个问题:一是文献[12]在光滑的前提下讨论了Pareto解,本文将其推广到非光滑条件下讨论Pareto解的存在性;二是首先给出Banach空间Pareto解的次可微形式的Pareto最优条件,然后,应用高次微分形式的泰勒公式来研究从Rn到Rm上的Ck,1函数的Pareto解的纯量形式最优性条件,最后,提出弱C-拟凸和C-拟凸函数的概念,并给出其二阶判别条件,完成对向量优化的高阶微分条件的进一步研究.
1 预备知识
下面给出本文用到的一些定义、性质及结论.
设Y是一个Banach空间,Y*是其对偶空间.记C⊂Y是一个内部非空集的闭凸锥,C+表示C的对偶锥,即 C+={y*∈Y*:0≤〈y*,c〉,∀c∈C},对y1,y2∈Y,定义关系 y1<Cy2和 y1≤Cy2分别为 y2-y1∈int(C)和 y2-y1∈C.
下面给出关于向量优化问题的一些结论及Pareto解的定义.
定理 1.1[11]设 f是从 Banach空间 X 到 Banach空间Y的一个映射X,f在的附近具有2n阶导数,其中n为一个自然数.假设存在c*∈C+,‖c*‖ =1且

若f(2n)(¯)是S正定,则是(1)式的局部Pareto解,并且存在数 η,δ∈(0,+∞)使

定理 1.2[11]设 f是从 Banach 空间 X 到Banach空间Y的一个C-凸映射X,f在的附近具有2n阶导数,其中n为一个自然数.假设存在c*∈C+,‖c*‖=1,若f(2n)(¯)是S正定,则是(1)式的整体 Pareto解,并且存在数η0∈(0,+∞)使

设WE(A,C)表示由A的所有弱Pareto有效点构成的集合,E(A,C)表示由A的所有Pareto有效点构成的集合,则显然有

设f是从Banach空间X到Banach空间Y的一个函数,考虑向量最优化问题

定理 1.3[11]设 f是从 Banach空间 X 到 Banach空间Y的一个映射X,f在的附近具有2n阶导数,其中n为一个自然数, )=0.

成立,其中

对于局部 Lipschitz函数,Clarke[15]为连续可微函数梯度的推广,提出了广义梯度概念.
定义 1.1[15]设 f(x)为开集 S⊂Rn上的局部Lipschitz函数,f(x)在点 x处沿 d∈Rn的广义方向导数定义为

广义方向导数有如下性质:
定理 1.4[15]设 f(x)为 Rn上的局部 Lipschitz函数,在点x∈Rn附近的Lipschitz常数为L,则有下述结论:
1)f0(x;d)作为 d的函数是次可加的和正则的,且满足|f0(x;d)|≤L‖d‖;
2)f0(x;d)作为 d 的函数是 Lipschitz;
3)f0(x;d)作为 d的函数是上半连续的;
4)f0(x;-d)= -f0(x;d),∀d∈Rn.
定义 1.2[15]设 f(x)为 Rn上的局部 Lipschitz函数,f(x)在x处的Clarke次微分定义为
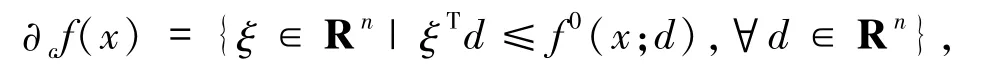
其中元素 ξ∈∂f(x)叫作 f(x)在 x处广义梯度.当f(x)为凸函数且连续时,则凸函数所定义的方向导数和次梯度相吻合,也就是

定义 1.3[15]设 A是 Y的一个子集且 a∈A.称:1)如果不存在点 y∈A\{a},使得 y<Ca,则 a是集合A中一个弱Pareto有效点;2)如果不存在点y∈A\{a},使得 y<Ca,则 a是集合 A中一个 Pareto有效点;3)如果对所有y∈A有a≤Cy,则a是集合A中一个理想点.
用 Ck,1(Rn,Rm)(k≥0)表示从 Rn到 Rm的具有直到k阶连续导数且其第k阶导算子是局部Lipschitz的函数全体.
用C0,1表示Rn上的局部Lipschitz函数全体,由 Rademaacher定理[15],对任意 f∈Ck,1,其 k 阶导算子Dkf是几乎处处可微的.定义f在点x∈Rn处的 k+1 阶次微分[15]为

称该集合的元为f在x处的k+1阶次梯度,它是Rn上的k重线性连续算子[15].
由文献[15]知∂k+1f(x)是非空紧集.
定义关于x,u∈Rn的双变量函数:
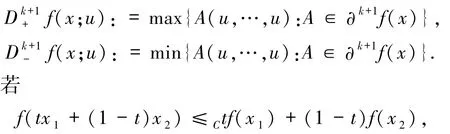
∀x1,x2∈X 且∀t∈[0,1],则映射f:x→y 是 C-凸的[3].
注1.1 f是C-凸的,当且仅当对所有 c*◦f是C-凸的.
2 一阶最优性条件的研究
在光滑假设的条件下,Zheng等[12]获得如下的结果.
引理 2.1[12]设 f:X→Y 是一个光滑映射且∈X,则如下结论成立:

对于C-凸函数,把上述光滑条件推广到非光滑条件下讨论Pareto解,给出下列次微分形式的结论.

其中∂表示凸次微分.

设 F(x):=f(x)+C,

容易验证A是凸的.
反证,若交集非空,则存在 x∈B(x,δ),y∈F(x)=f(x)+C,使得 y∈ f(x)-int C.设:y:=f(x)+c0,c0∈C,则

因此,存在η>0,使得


又由分离定理可知,存在(x*,c*)∈X*×Y*且‖(x*,c*)‖ =1,使得对所有(x,y)∈A,u∈X,c∈int C,有

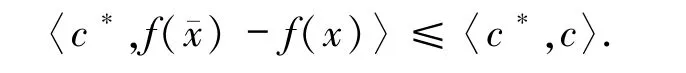
又因为 f是 C-凸的,(c*◦f)是凸的,且 0∈∂(c*◦f)),故对任意的x∈),c∈C+且‖c*‖=1.
反之,假设f是C-凸,c∈C+且‖c*‖=1使得(3)式成立,则对于一固定点x∈X,有
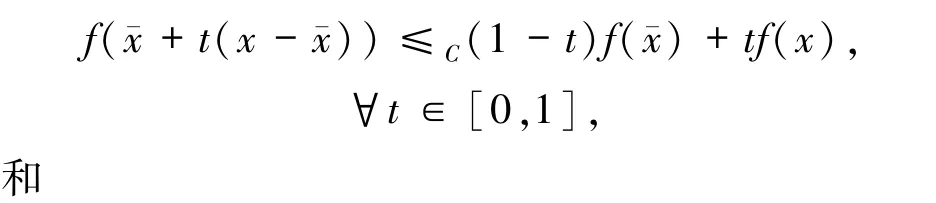
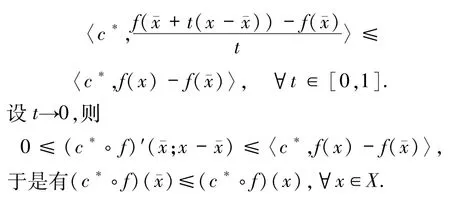
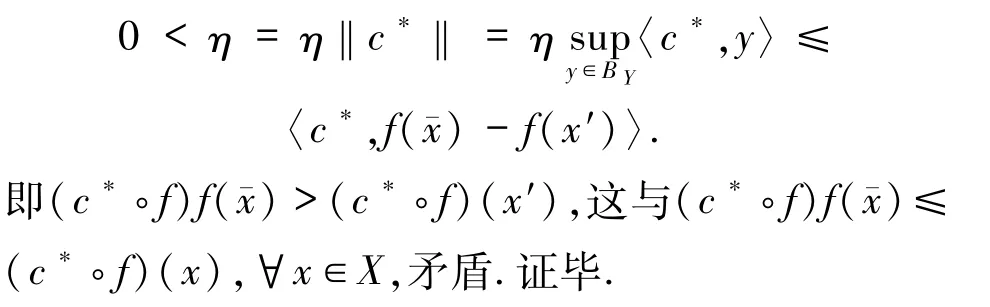
证明 设h是X中任意一点,c*∈C+中,则存在δ>0,使得对于所有的t∈(0,δ)有f()≤cf(+th).因此,对于所有的 t∈(0,δ)有
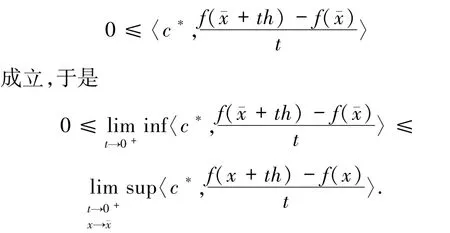
因此0∈∂c(c*◦f)().证毕.
(ii)对于所有的c*∈C+有0∈∂(c*◦f)(;
证明 因f是连续的C-凸映射,对于所有c*∈C+,有∂(c*◦f)()=∂c(c*◦f)(),由命题2.3 立刻有(i)⇒(ii),只需证明(ii)⇒(iii).先假设(ii)成立,设 x∈X 和c*∈C+,由 C-凸性可知
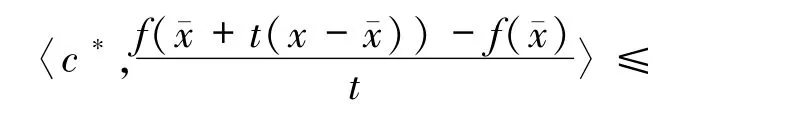

由(ii)可知0≤(c*◦f)′)≤〈c*,f(x)-f()〉成立.因此对于所有的x∈X,有(c*◦f)()≤(c*◦f)(x).
〈c*,f(x′)-f)〉< 〈c*,c〉, ∀c∈C成立.因 C 是闭凸锥,则 0≤〈c*,c〉,∀c∈C 和(c*◦f)()> (c*◦f)(x′),c*∈C+,矛盾.证毕.
3 k+1阶次微分最优性条件的研究
由Taylor公式知道,当X是有限维的且f:X→R是2n次可微的¯∈X.如果f(k)(¯)=0(k=1,2,…,2n-1),且对任意的 h∈X\{0}都有 f(2n)h(2n)>0,则¯是f的一个局部极小值点.对多目标优化问题,许多研究者考虑了二阶优化条件,给出了不同形式的优化条件.参考文献[14],利用高阶Clarke次微分形式的Taylor公式,给出有限维空间上的Ck,1类向量值函数的(k+1)优化条件.
设 f:Rn→Rm,C⊂Rm是闭凸锥且 f∈Ck,1.
引理 3.1[14]设 f∈Ck,1(Rn,R),a,b∈Rn,则存在 c∈(a,b)及 A∈∂k+1f(c),使得

引理 3.2[14]设 f∈Ck,1(Rn,R),a,x∈Rn,则存在Ax∈∂k+1f(a)及 Rn上的 n重线性连续算子r(x),使得

根据引理3.1得到如下结论.
命题3.1 设f∈Ck,1(Rn,Rm)Rn是(2)式的一个局部理想解,如果Dif(¯)=0(i=1,2,…,k),那么对于所有的u∈Rn和c*∈C+有

成立.特别地,如果k是偶数,那么对于所有的u∈Rn有0∈∂k+1f(c*◦f)¯;u).
证明 令c*∈C+.因为Di(c*◦f)()=(c*◦Dif)()=0,i=1,2,…,k,(c*◦f)是一个从Rn到R的k次可微映射,其k阶导数是也是局部Lipschitz的并且(c*◦f)在处取局部最小值,应用引理3.1,得证.
对于函数Ck,1以k+1阶次微分的形式,为成为(2)式的尖的局部Pareto解提供高次充分条件.
定理3.1 设f∈Ck,1(Rn,Rm),Rn,且)=0,i=1,2,…,k.假设存在c*∈C+且‖c*‖ =1,对所有的 u∈Rn,u≠0 有


证明 对于所有的 x∈X,设 φ(x):=〈c*,f(x)〉,那么 φ 是一个从 Rn到 R 的 Ck,1函数.由引理3.2知,存在A∈∂k+1φ()及Rn上的n重线性连续算子r(x),使得
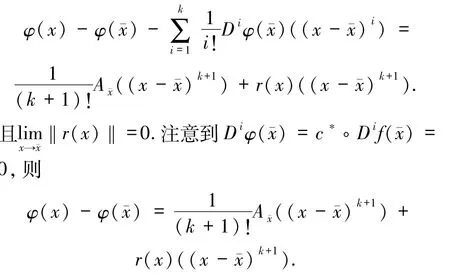
令S:={x∈Rn:‖x‖ =1}.由(c*◦f)的定义可知,函数u→(c*◦f)(;u)是连续的,注意到S是紧集,故存在u′∈S,使得
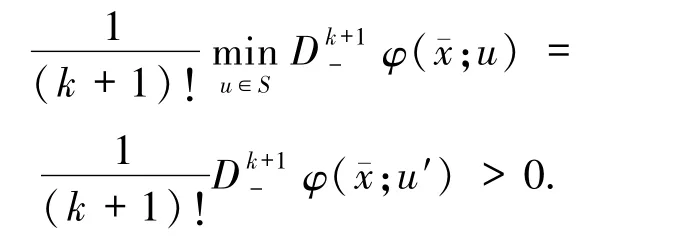

对C-凸且是Ck,1的函数,提供一个使成为(2)式的整体的Pareto解的高阶充分条件.
定理 3.2 设 f∈Ck,1(Rn,Rm)且是 C- 凸的,再设x¯∈Rn,Dif(x¯)=0,其中i=1,2,…,k.假设存在c*∈X*且‖c*‖=1,对所有的u∈Rn,u≠0有)>0,那么,x¯是(2)式的整体的Pareto解且存在η0∈(0,+∞)使得下面结论成立:

证明 与定理3.1最后的证明方式相同,(6)式成立意味着是(2)式的全局的Pareto解.只要证明(6)式成立即可.根据定理3.1,这里存在 η,δ∈(0,+∞)使得(2)式成立.

取 η0:= min{η,ηk+1δk},从(5)式知(6)式成立.证毕.
在更强的假设下,有以下(2)式整体理想解的充分条件.
定理3.3 设f∈Ck,1(Rn,Rm)且∈Rn.假设=0,i=1,2,…,k,且对于任何x,u∈Rn,u≠0,c*∈C+,都有◦f)(x;u)>0,那么是(2)式理想解.
证明 对于任何 x∈X,设 φ(x):=〈c*,f(x)〉,那么 φ 是 Rn到 R 的 Ck,1函数,令 u∈Rn,u≠0,由引理3.2,存在v∈(,x+u),使得

故对∀x∈X,有(c*◦f)()≤(c*◦f)(x).根据分离定理[16],易知¯是(2)式理想解.证毕.
4 k+1阶拟C-凸函数的判别条件的研究
参见文献[15,17-21],得到如下概念.
第一,设 f:Rn→R,称 f是拟凸的,如果对任意x,y∈Rn且 λ∈(0,1)都有

凸函数和拟凸函数都可以通过一阶和二阶次微分刻画.
第二,设 f是从Rn到Rm的函数,如果存在c*∈C+,使得对任意 x,y∈Rn且 λ∈(0,1),使得

则称f是弱C-拟凸函数.如果对任意c*∈C+,任意 x,y∈Rn且 λ∈(0,1),(7)式都成立,则称 f是C-拟凸函数.
文献[14]运用广义Heshiang给出拟凸函数的二阶判定准则.在此,给出C-拟凸函数和弱C-拟凸函数的k+1阶判定准则.
命题 4.1 设 f∈Ck,1(Rn,Rm),f是 C- 拟凸函数(或弱C-拟凸函数),k是奇数且C⊂Rm是闭凸尖锥.若 x,u∈Rn,使得 )= 0 ,则对任何(或存在)c*∈C+,使得

证明 假设结论不正确,那么存在x,u∈Rn,c*∈C+,使得


由引理3.1,存在 v∈(x,x+tu)和 A∈∂k+1(c*◦f)(v),v使得
(c*◦f)(x+tu)- (c*◦f)(x)= tk+1Av(u,…,u).
又由假设k为奇数,则对所有的 t∈[-t0,t0],有
(c*◦f)(x+tu)- (c*◦f)(x)< - ε < 0.特别地,

特别地,如果 m =1,C=R+,那么 C+=R+,有:
推论4.1 设f是从Rn到R的拟凸函数,k是奇数.如果 x,u∈Rn, (x)(ui) = 0 ,则f(x;u)≥0.
另外,关于充分性二阶条件,应用命题4.1,立刻得出以下推论.
推论 4.2 假设 f∈C1,1(Rn,Rm),任取 x,u∈Rn,x≠u,如果对任意 c*∈C+,当 D(c*◦f)(x)(u)=0时,有(c*◦f)(x;u)≥0;当 D(c*◦f)(x)=0时,有(c*◦f)(x;u)> 0;则 f是 C- 拟凸函数(弱C-拟凸函数).
现在假设:f:Rn→Rm是一个 C1,1和 C- 凸函数,C⊂Rm是闭凸尖锥.令∈Rn,cj∈R,和 P:= {x∈Rn:〈,x〉-cj≤0;j=1,2,…,k}.考虑如下的C-凸向量优化问题:

3)存在c*∈C+\{0}和tj≥0(j∈I()),使得

与命题4.2类似,对优化问题(8)的理想解,有

反之,任取c*∈C+.假设存在tj≥0(j∈I())使得(10)成立.由(9)式可知,一定有0∈φ′c*()+N(P,).因为φc*是凸的,则是φc*在P上的一个极小值.因此,对任意x∈P,有f()≤Cf(x),由此可知,对任意x∈P和c*∈C+,都有〈c*,f()〉≤〈c*,f(x)〉.所以是(8)式的一个理想解.
根据命题2.4及命题4.1,得到如下结论.

