脉冲星导航的天体测量考虑
李亮,王广利,郭丽,胡小工
(1. 中国科学院 上海天文台,上海 200030;2. 中国科学院大学,北京 100049)
0 引 言
纵观人类航天活动发展史,航天器的活动范围已覆盖近地、深空乃至星际空间,确定航天器的空间位置已经成为所有任务的关键。继惯性导航、无线电导航、光学导航等导航技术后,由于X射线脉冲星导航具有适用空间范围广、自主性高、系统简单等特点,近年来受到国内外研究学者的极大重视。脉冲星导航概念最早由Downs提出[1],其建议在飞行器上搭载 2 m射电望远镜观测脉冲星进行导航,但是脉冲星射电流量微弱,射电波段观测脉冲星需要大口径望远镜。
为了避免需要大尺寸望远镜的问题,Chester和Butman提出了基于X射线脉冲星观测的导航方法[2]。在此基础上,Wood首次提议在ARGOS(Advanced Research and Global Observation Satellite)星上进行导航试验[3],并基于掩星法,他提出了航天器姿态确定和时间保持的方法。在Wood工作的基础上,Hanson[4]提出了利用X射线脉冲星进行卫星姿态测量的方案,并利用HEAO-A1卫星进行试验,其仿真结果显示姿态确定的精度能够达到0.01°,时间保持的精度约1.5 ms。随后,多位学者也聚焦于X射线脉冲星导航领域并推动其发展,如Sheikh系统研究了脉冲星导航各方面内容[5],Emadzadeh和Speyer对脉冲星信号模型和导航算法进行了详细的讨论[6]。特别是在美国国防部先进研究计划局(Defense Advanced Research Projects Agency,DARPA)提出XNAV(X-ray Source-based Navigation for Autonomous Position Determination)计划之后,脉冲星导航得到了长足的发展。
尽管脉冲星导航概念和理论基础比较成熟,但有些脉冲星导航的天体测量概念仍值得强调,本文旨在重点梳理这部分内容。第1部分介绍脉冲星观测模型,梳理脉冲星观测数据处理流程;第2部分分析观测量的获取、整周模糊度和脉冲星导航应用范围3个具体问题,阐明这些问题产生的原因和解决方案;最后部分是本文的总结。
1 脉冲星观测模型
脉冲轮廓是辐射流量随相位变化的函数,是脉冲星观测的实测值。将观测得到的平均脉冲轮廓(观测轮廓)与标准轮廓相关,可得到观测轮廓的到达时刻(Time of Arrival,TOA)。TOA是指平均脉冲轮廓上某一点所确定的时刻,通常选取的参考点为辐射流量最高点。脉冲星观测的目的是得到观测轮廓,进而计算观测轮廓的TOA,建立TOA和各因素的数学模型,从而解算模型中部分待定参数。
1.1 脉冲星射电观测模型
脉冲星射电观测的直接测量为辐射流量随时间变化的序列,记为m(t),其中。脉冲星的流量非常微弱,对于大部分脉冲星来说,脉冲信号会淹没在噪声之中,测量所得的m(t)无法体现脉冲轮廓。由于脉冲星信号具有周期性,且发出的辐射总是来自于同一相位,可以将不同周期中同一相位的信号叠加,噪声由于其随机特性而被抑制,脉冲信号得以增强,能够得到具有一定信噪比的观测轮廓。
t时刻的相位表达为

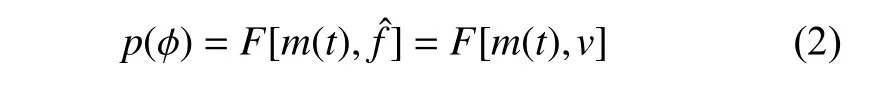
根据观测和观测者的速度,可以得到观测轮廓。如图1所示,将观测轮廓与标准轮廓相关,得到观测轮廓的TOA。蓝色的线为标准轮廓,其辐射流量最高点的相位为,红色的线为观测轮廓,其在ts时刻的相位为。将观测轮廓和标准轮廓相关,得到相位差,观测轮廓到达测站的时刻(Site Arrival Time,tsat)表示如下
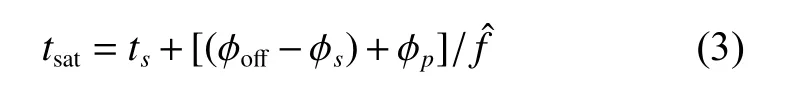
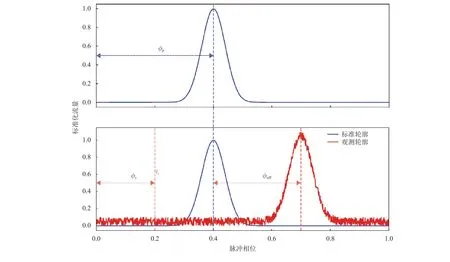
图1 观测轮廓和标准轮廓
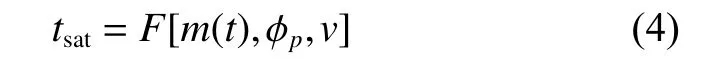
根据观测者的位置,将观测脉冲到达测站时刻转换为观测脉冲到达太阳系质心时刻(Barycenter Arrival Time,BAT),tbat近似表达式为

根据脉冲星自转模型,可计算tbat时刻的脉冲相位。据此,可建立射电脉冲星观测的误差方程为
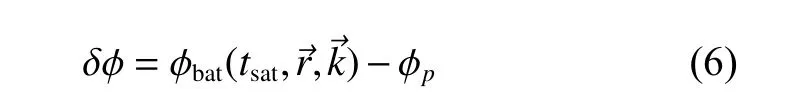
1.2 脉冲星X射线观测模型
根据观测者的位置,将每个光子的到达时刻转换为光子到达太阳系质心处的时刻


并最终建立X射线脉冲星观测的误差方程。比较式(4)和式(8),观测者处叠加得到轮廓无需已知测站的位置,但依赖于观测者的速度,太阳系质心处叠加得到轮廓则与之相反。射电波段脉冲星观测只能采取第一种处理方式;X射线波段脉冲星观测由于记录的是每个光子的到达时刻,可以采取上述2种方式,由于第2种方式无需已知测站速度,目前X射线脉冲星观测采用的是后者。
2 脉冲星导航的天体测量问题
2.1 观测量的获取
脉冲星导航首先需要考虑的问题是观测量的获取。根据前文的描述,获取观测量的方式有2种。下面分别考虑获取观测量所需的条件。
采用观测者处叠加获取观测量,需要已知脉冲星的视频率。脉冲星的视频率根据观测者的速度计算为

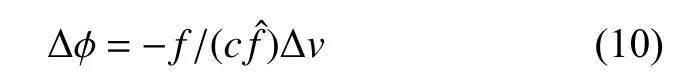
在整个观测时间段内,引起的最大相位差为

一般来说,要求最大相位差不超过脉冲轮廓的一个 bin,记脉冲轮廓共划分了个bin,则在总观测时间内,对观测者速度的要求为
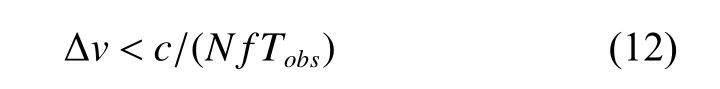
若采用太阳系质心叠加轮廓的方式,要求每个光子相位误差不超过1/10个bin,在总观测时间内,要求观测者的位置精度为

bin的选取原则与脉冲星信号强度、积分时间、接收面积等有关,需要保证每个bin里有一定数量的光子。目前,大部分X射线脉冲星观测所选取的bin 为100。若假设脉冲星的周期为10 ms,脉冲轮廓划分为100个bin,观测时间为1万s,则要求观测者的速度好于3 m/s,或者要求观测者的位置好于3 km。
脉冲星导航的目的是确定观测者的位置和速度,而得到观测量的前提是需要速度或位置的先验信息满足一定要求。在观测者速度和位置未知或误差较大时获取观测量是脉冲星导航首先需要考虑的问题。目前,部分脉冲星导航研究忽视了该情况,默认观测者位置精确已知并获得了脉冲轮廓,这是不合理的,若观测者位置精确已知也就无需脉冲星导航了。同时,观测值位置初值的偏差也影响导航过程的解算,需要尽可能多地观测多颗分布均匀的脉冲星,减少设计矩阵的奇异性。本文仅从观测量获取角度论述了对初值的要求,但初值精度对导航解算同样重要。
根据Sextant试验结果[7],目前脉冲星导航精度在十几千米的水平。若采用太阳系质心叠加轮廓的方式,要求观测者的初始位置的“波动精度”好于几千米,即初始位置的整体偏差对该问题无影响,但扣除整体偏差外的误差不应该大于几千米。而脉冲星导航精度在10 km量级,采用该方式得到观测量进行导航会陷入需要较精确轨道的陷阱。同时,该方式的导航误差方程将难以线性化,会给解算带来额外的问题。脉冲星导航应该在观测者处叠加,获得脉冲轮廓,从而获得脉冲到达观测者的时刻。根据前文的论述,我们的目的是需要在观测者速度未知或误差较大时得到脉冲轮廓。假设观测者的速度为,叠加生成的轮廓为,定义该观测轮廓的显著性为。若观测者的速度偏差越小,则观测轮廓的显著性越大,即:
在观测者速度未知的情况下获取观测轮廓的问题转换为式(14)最优化问题。
脉冲星导航需要在观测者处本地叠加轮廓,通过最优化观测轮廓确定观测者的速度,从而确定观测轮廓。最优化观测轮廓仅与观测者的速度(位置的变化)有关,并不能确定观测者的绝对位置。采用最优化观测轮廓可以确定观测者速度,进而得到观测量,但利用最优化轮廓方法直接导航从原理上是行不通的。
2.2 整周模糊度
整周模糊度问题是脉冲星导航的另一个难点。整周模糊度问题是指观测得到的相位与模型预报的相位可能存在整周差,即脉冲星导航的误差方程为
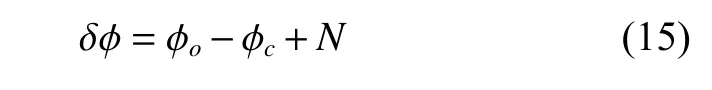
为了简化问题的描述,我们将空间模糊度搜索简化为平面模糊度搜索,其揭示的原理一致。如图2所示,图中网格虚线对应于脉冲星相位整周,虚线之间的距离为脉冲波长。虚线由脉冲星方向和脉冲星自转模型确定,与脉冲星导航观测无关。灰色部分为模糊度搜索空间,由观测者的初始位置等因素确定。搜索空间中红黑虚线的交点是模糊度候选解,如图中假设观测者共观测了k颗脉冲星,其观测相位分别为,观测误差为。根据观测相位和,有


图2 整周模糊度求解几何示意图

根据观测者的候选位置,推算其余脉冲星的观测相位和整周模糊度为

记观测相位与推算出的相位差为

使得式(19)范数最小的候选解为整周模糊度解为
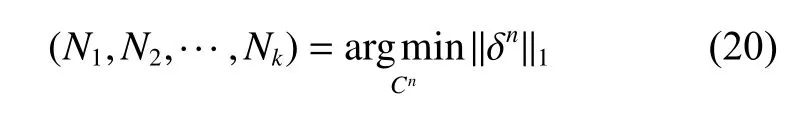
由于观测误差的存在,式(20)可能没有解或存在错误的解。减少观测误差和增加脉冲星数量能够有助于得到正确的解,对于脉冲星导航来说,至少需要观测4颗脉冲星才能解决模糊度问题。
2.3 应用范围
脉冲星导航的目的是确定观测者的位置和速度,其相关的理论研究和试验不应该基于精确已知的位置和速度,这是目前部分研究所忽视的问题。根据前面的分析,可以看出脉冲星导航能否应用的关键是观测量的获取,即式(14)是否可解。式(14)中的是观测者速度在脉冲星方向的投影,是一个随时间变化的量。由于脉冲星X射线光子较少且背景噪声较大,同时每个光子对应的都不相同,已有的信息无法直接解算序列,需要采用一个简单的模型来描述观测者速度,从而仅需要求解模型中的少量参数来求解序列。也就是说,脉冲星导航能够应用的前提是观测者的速度在脉冲星方向上的投影对导航观测量的影响能够得到处理。本文采用多项式拟合进行简单尝试。脉冲星导航需要观测多颗脉冲星,假设脉冲星的方向为,则
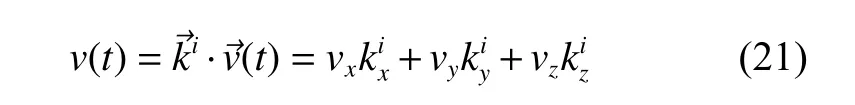
为了探讨脉冲星导航能否应用于近地空间问题,我们构建了一个近地空间卫星星座,该星座的轨道半径为27 878.137 km,偏心率为0.01,轨道倾角为 55°。共3个轨道面,每个轨道面平均分布8颗卫星。根据动力学关系和给定的初值,我们精确积分出了其近地空间卫星星座2018年3月22—25日的轨道,并分析利用低阶多项式描述速度的可行性。
由于所有数据具有类似的结果,这里仅展示其中一颗卫星的结果。假设观测时间为1万s,查看该观测时间内速度是否可以采用低阶多项式拟合。从生成的轨道数据中提取1万s速度数据,每次往后滑动5分钟,共830段数据。对每段数据分别采用三阶多项式拟合速度分量,拟合结果如图3所示。
图3上半部分为拟合的速度残差。假设脉冲星的周期为 10 ms,则三阶多项式拟合速度的偏差引起的最大相位偏差如图3下半部分所示,满足周期叠加得到观测轮廓的要求。大体上,脉冲星导航是可以应用在近地空间的,低阶多项式对观测者速度的描述满足观测要求。至于该采用几阶多项式描述观测者的速度,应该根据具体轨道和观测积分时间而决定。
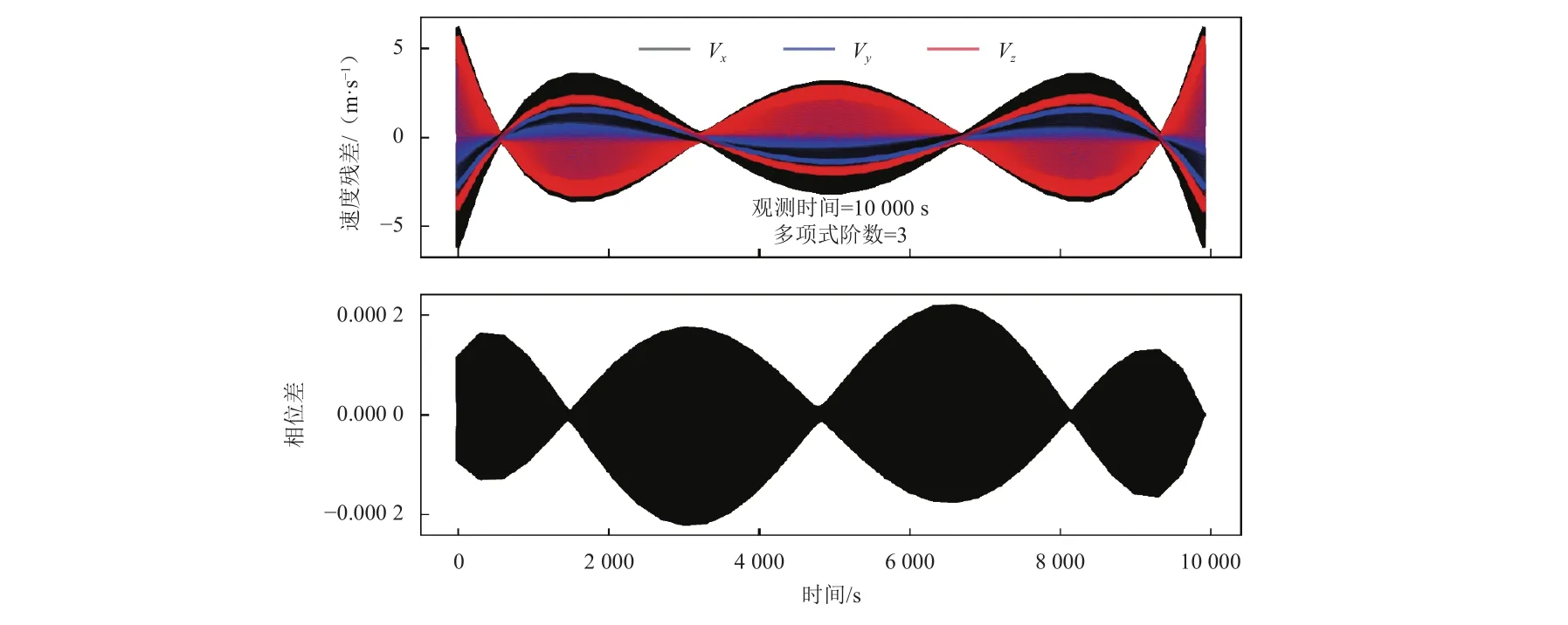
图3 三阶多项式拟合速度的残差和引起的相位差
对于超深空脉冲星导航,脉冲星位置误差是制约导航精度的主要因素。图4为部分典型导航脉冲星的位置误差和流量图。一般来说,X射线流量高的脉冲星为年轻脉冲星,其自转不稳定,计时结果得到的位置误差较大。图5为上述导航脉冲星的位置误差引起的导航偏差。若选取流量较强的脉冲星进行导航,则其位置误差较大,将影响导航精度,若选取位置精度高的脉冲星进行导航,则其流量较弱,需要大面积观测仪器和长时间积分观测。此外,对于100 AU以外的超深空导航,脉冲星观测位置误差制约着导航精度,而且脉冲星计时位置误差取决于其自身自转稳定性,与技术发展无关,精度提升有限。
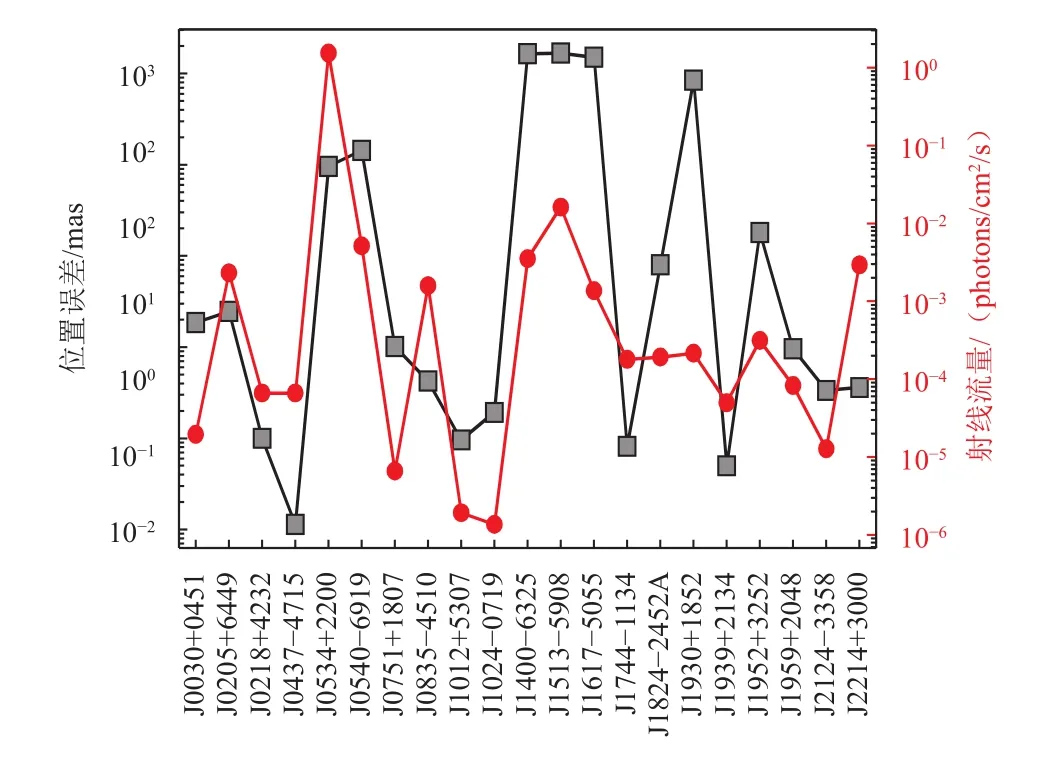
图4 导航脉冲星的位置误差和X射线流量
3 结束语

图5 导航脉冲星位置误差对导航位置精度的影响
X射线脉冲观测需要已知观测者的速度,若观测者的速度在脉冲星方向上的投影对导航观测量的影响能够得到处理,如采用多项式模型进行描述,通过最大化观测轮廓可以确定观测者的速度,从而得到观测量。最大化观测轮廓仅能确定观测者的位置变化,并不能确定观测者的绝对位置,最大化观测轮廓从理论上无法导航,脉冲星导航应基于TOA序列观测数据。
模糊度问题仍是制约深空导航成败的主要因素,搜索方法有可能无法得到正确的解,或需要采用其他导航手段来确保模糊度的解算。对于超深空导航,导航的精度与距离太阳系质心的距离有关,脉冲星导航是否能成功应用超深空还有待进一步研究。

