基于高斯伪谱法的火星表面上升燃耗最优轨迹设计

柯森锎，李爽，肖东东，王卫华，聂钦博

（1. 南京航空航天大学 航天学院，南京 210016；2. 南京航空航天大学 航天新技术实验室，南京 210016；3. 上海航天控制技术研究所，上海 201109）

0 引 言

火星是离地球最近的类地行星，对火星的探测有助于人类进一步理解认识太阳系的起源和演变，将宇宙科学推上新台阶[1]。在人类成功实施火星着陆探测之后，采样返回将是火星探测的下一个里程碑[2-3]。火星上升器（Mars Ascent Vehicle，MAV）发射总质量是关系到火星采样返回任务可行性的关键因素，不仅关系到所能携带的火星样本的质量，而且直接影响火星表面上升轨迹设计。同时，它也关系到火星发射支持系统的质量，进一步影响到火星登陆器的质量，最后传导到地球上火箭的运载能力要求上。MAV每增加1 kg，则地球发射质量将相应增加约8 kg[4]。而在当前技术条件下每将1 kg的有效设备送上火星需要花费约100万美元的成本[5]。所以MAV的设计不仅需要考虑火箭的运载能力、火星进入下降着陆（Entry，Descent and Landing，EDL）能力的可行性约束[6]，还面临着经济性的考虑。

为了实现最轻的火星上升器设计，必须对MAV分级参数和上升轨迹进行优化。上升器参数包括各级火箭的干重、燃料质量、推力、比冲等。轨迹优化的经典应用领域为火箭的最优控制问题[7-10]，在该问题中给定火箭参数，要求以燃耗最优为目标函数进行轨迹优化以得到最优的控制量。Betts对轨迹优化问题的求解方法进行了概括分析，将其分为解析法和数值法，其中数值法又可以分为直接法和间接法[11]。高斯伪谱法是直接法的一种，Patterson提出了一种自适应的高斯伪谱优化方法并开发了相应的Matlab软件GPOPS-II[12]。国内的杨希祥基于高斯伪谱法做了固体火箭快速轨迹优化研究[13]。如果火箭分级参数设计得不合理，那么轨迹优化问题就无法收敛得到理想的优化结果，针对这一问题Coskun提出了一种基于高斯伪谱法的优化方法，能够将火箭分级优化和轨迹优化耦合[14]。Benito也将高斯伪谱法引入到MAV的上升轨迹优化问题中来[15]。

本文以火星上升器总发射质量最小为目标函数，基于高斯伪谱法设计了一种针对两级MAV的分级与轨迹耦合多阶段优化算法，最终得到MAV总发射质量最小的火星上升器分级参数以及一条燃耗最优上升轨迹。

1 问题描述

1.1 飞行方案

在火星表面发射入轨所需的速度增量与地球相比大大减小，适合采用两级MAV设计。本论文中上升器从火星表面起飞入轨的飞行方案如图1所示，第1级点火开始是一个很短的大推力的动力上升段；然后是长时间的无动力滑行段一直到上升轨道的远拱点处；进一步在远拱点处第2级火箭点火进行轨道圆化进入目标圆轨道，然后释放火星样本舱，最终由火星轨道器实现对火星样本舱的交汇捕获以及返回地球[16-18]。

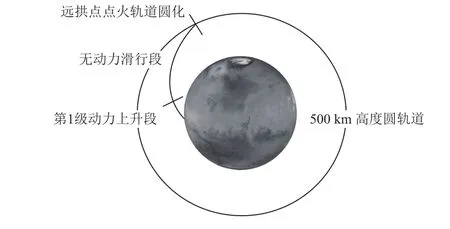
图1 火星上升器飞行方案Fig. 1 MAV fly profile

1.2 坐标系定义

1.3 两级MAV质量模型

一个一般化的两级MAV的质量模型如图2所示。每一级的质量由干重和燃料质量组成[19]。而每级干重又由固定质量和与燃料质量相关的可变质量组成。

图2 一般化的两级MAV质量模型Fig. 2 The universal model for 2-stage MAVs

燃料质量由每级的干重、载荷质量、速度增量以及燃料比冲决定，燃料质量为

第1级的载荷包括第2级总质量加上有效载荷的质量。

1.4 动力学模型

假设火星为旋转的标准圆球，只考虑空气阻力作用，在火心惯性直角坐标系下建立MAV上升段的动力学方程为

2 两级MAV的分级与轨迹耦合多阶段优化算法

将两级MAV的总发射质量最小化问题转化为两级MAV的分级与轨迹耦合多阶段优化问题。根据两级MAV的飞行方案将两级MAV的分级与轨迹耦合优化问题分为3个阶段：动力段、滑行段、圆化段。

2.1 目标函数与优化变量

对于MAV的总发射质量最小化问题，其目标是使得总发射质量最小，等效于最小化第一阶段的初始质量，其目标函数为

2.2 动力学约束

动力学约束由第1节中的动力学模型给出。由于MAV总发射质量最小化问题需要对各级燃料质量进行优化，所以增加了消耗的燃料质量作为状态量，需要增加式（10）所示的微分方程作为动力学约束。

其中：p为消耗的燃料质量。

2.3 边界约束

本节将给出MAV总发射质量最小化问题各阶段的边界约束条件。

1）第1级推力段

2）无动力滑行段

无动力滑行段的初始条件由第1级推力段的终端状态给出，即由2个阶段的连接点约束决定。

为了增加MAV进入火星稳定轨道的概率，MAV将一直滑行到滑行轨道的远拱点再进行轨道圆化，即该阶段的终端约束为径向速度为零，即

3）轨道圆化

该初始条件由滑行段的终端状态给出，由两个阶段的连接点约束决定。在此阶段的开端MAV进行一、二级火箭分离，抛弃第1级的同时第2级火箭点火进行轨道圆化，所以第2级轨道圆化段与无动力滑行段间的连接点约束要考虑第1级干重质量。连接点约束为

将第2级轨道圆化段的初始燃料消耗质量设置为零，即

该阶段的终端条件为进入目标轨道，即满足给定的轨道要素，与轨迹优化问题类似，但是需要增加终端质量约束为

升交点赤经可以通过改变发射时间来调整，因此本文中不考虑升交点赤经约束，目标轨道为圆轨道所以为目标轨道高度。虽然圆轨道是数学上最简单的轨道，但是在现实中由于各种扰动很难实现精确的圆轨道，如果将离心率设为零将会带来一些数值计算上的困难，比如伪震荡和不收敛。对于引入误差范围如下式所示。

2.4 路径约束

1）第1级推力段

飞行高度约束

动压约束

推力角约束如式（31），推力角为推力方向与相对火星速度的夹角，其计算方程如式（32）所示，由于使用3DoF模型无法表示攻角，用推力角近似攻角。

2）无动力滑行段

该阶段的飞行高度约束以及动压约束与第1级推力段相同，因为整个过程没有推力，所以并没有推力方向和推力角约束。

3）轨道圆化段

该阶段在大气层外所以无需考虑动压和推力角约束，但推力方向和飞行高度约束与第1级推力段相同。

3 高斯伪谱法

高斯伪谱法属于直接法中的配点法，在处理分级与轨迹耦合优化问题时，通过在一系列拉格朗日高斯（Legendre Gauss，LG）点上构建拉格朗日多项式来逼近状态变量和控制变量[13]，进一步对得到的多项式求导来近似状态量的导数，将微分方程转换为代数方程。对于终端条件和目标函数中的积分项使用高斯积分来替换，将积分方程也转换为代数方程，把分级与轨迹耦合优化问题离散后转换为非线性规划问题[进行]求解。

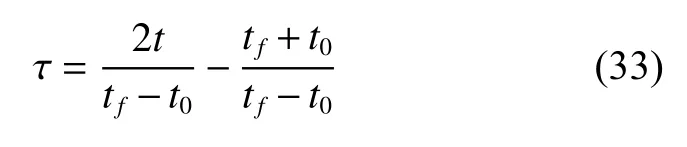
对（34）求导可以得到状态量关于时间的导数为

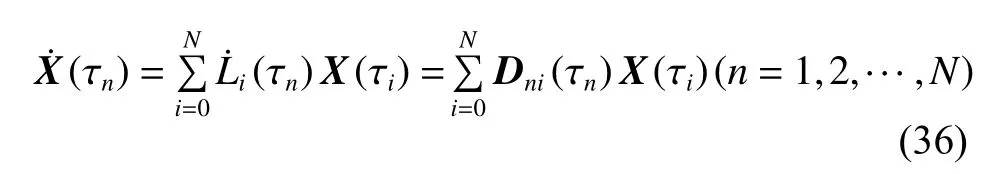
基于式（36）可以将LG点处的动力学方程约束转换为代数方程形式为

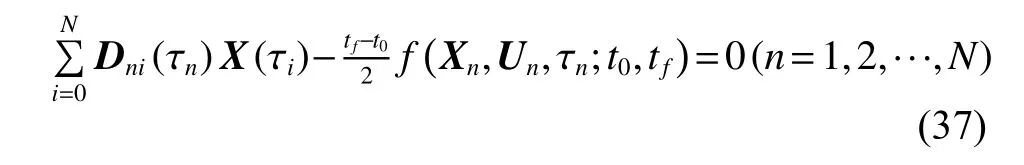
终端状态也需要满足动力学方程约束，将动力学方程从初始时刻积分至终端时刻可以得到终端状态量，使用高斯积分近似积分项，可以得到终端状态量为

加上各离散点处的边界条件和路径约束就可以将两级MAV分级与轨迹耦合优化问题离散化为非线性规划问题，求得满足约束条件的状态量和控制量使得目标函数最小。

4 仿真实验与分析

对提出的基于高斯伪谱法的两级MAV的分级与轨迹耦合多阶段优化算法仿真，目标轨道参数、发射点位置以及两级MAV质量模型参数的详细输入值都由表1给出[19]。仿真程序在Matlab环境下运行，计算机CPU为2.67 GHz Core i5，仿真计算得到两级MAV的分级优化结果如表2所示，同时得到一条标称上升轨迹如图3～9所示。

表1 两级MAV分级与轨迹耦合优化算法仿真输入参数Table 1 Input parameters of two-stage MAV coupled stagingtrajectory optimization algorithm simulation

表2 两级MAV分级优化结果Table 2 The result of two-stage MAV staging optimization

图3 上升高度随时间变化曲线Fig. 3 Altitude vs. time

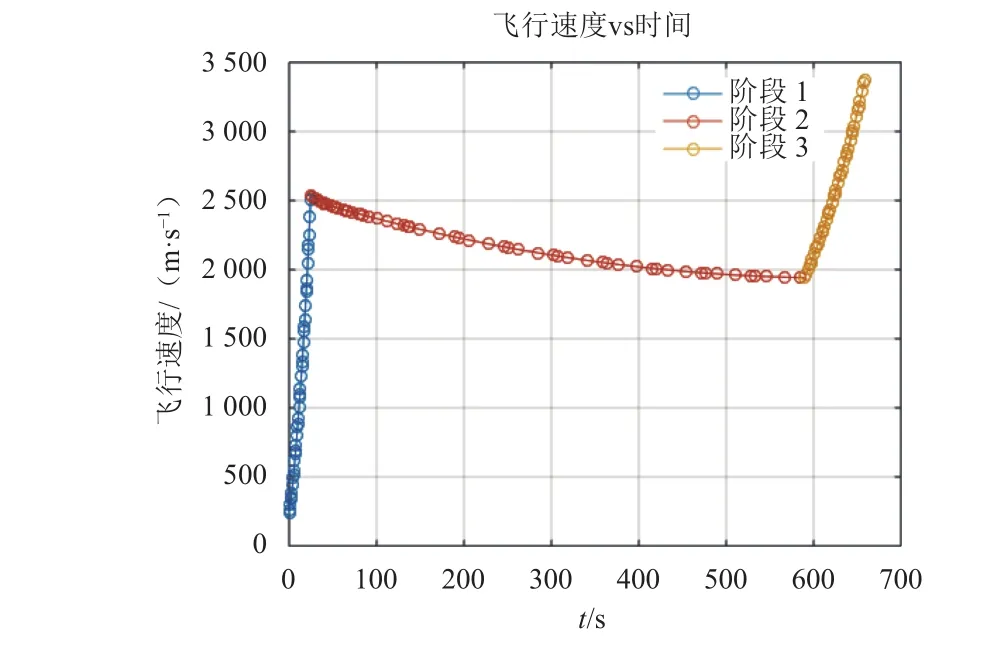
图4 飞行速度随时间变化曲线Fig. 4 Speed vs. time

图5 轨道倾角随时间变化曲线Fig. 5 Inclination vs. time

由图3～5可知滑行段时间约为565 s，燃耗最优的轨迹并不是在第1级耗尽时达到目标轨道倾角，而是留下约2.5°的轨道倾角误差留给第2级进行调整；由图6～7第1级控制量可得发射方位角为42.5°，仰角为40.5°，第2级进行轨道圆化的推力方向接近于固定方向；由于MAV的气动阻力系数Cd在这里被设定为简单的恒定值0.2[21]，所以得到的动压值只能作为一个概略的定性值，由图8知由于燃烧时间短，第1级耗尽点高度较低，在第1级耗尽点处达到了动压的峰值，可以考虑增加燃烧时间以提高耗尽点高度，以降低耗尽点的动压使其为在峰值之后的一个较小值，可以减小滑行段姿态保持的难度；图9中第1级的推力角起始值约为60°，之后快速减小并保持在5°以下，这是因为推力角是推力与MAV相对火星速度的夹角，而在起始时刻MAV相对火星速度为零，这里的起始推力角是由数值计算误差得到的。

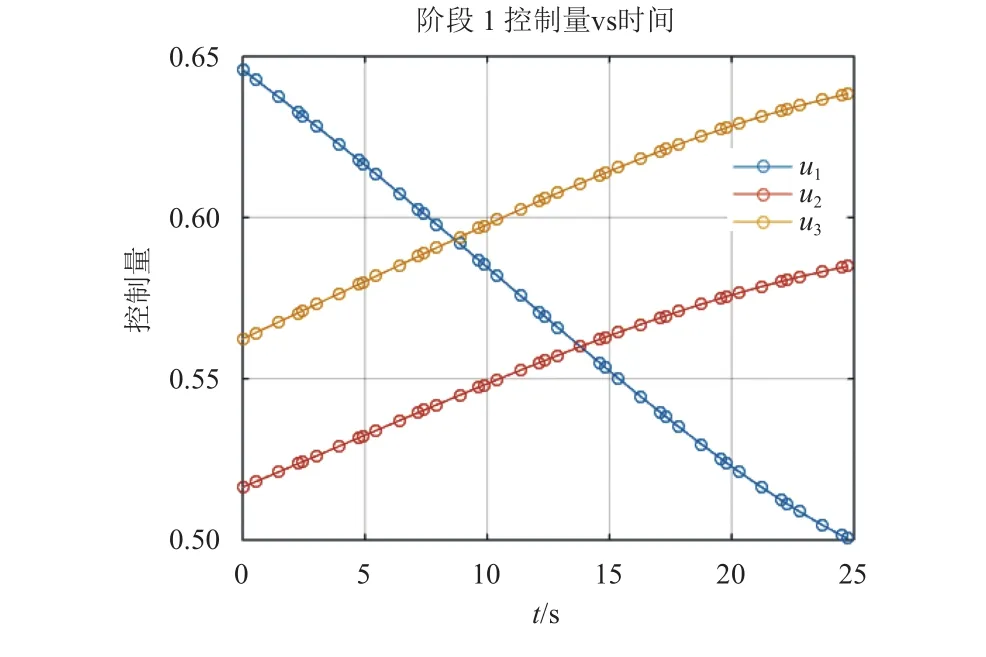
图6 第一阶段的控制量随时间变化曲线Fig. 6 Control vs. time for phase 1

图7 第三阶段的控制量随时间变化曲线Fig. 7 Control vs. time for phase 2

图8 动压随时间变化曲线Fig. 8 Dynamic pressure vs. time

图9 第1级推力角随时间变化曲线Fig. 9 Thrust angle vs. time for phase 1

通过仿真计算可知，该优化算法的初值在给定范围内随机选取都能在约7 min内收敛得到最优结果，计算精度达到10-6量级。

5 结 论

以火星采样返回任务中的两级火星上升器为研究对象，利用高斯伪谱法设计了在复杂多约束条件下两级MAV分级与轨迹耦合多阶段优化算法，以求得总发射质量最小的两级MAV分级设计以及燃耗最优的上升轨迹。该算法将MAV的分级优化与轨迹优化耦合在一起，解决了由于不合理的分级参数导致轨迹优化无法收敛的问题。通过仿真验证可以得到如下结论。

1）为达到燃耗最优的目的，两级MAV的第1级将留下一定的轨道倾角偏转量由第2级完成。

2）为减小两级MAV在滑行段的姿控难度可以适当减小第1级火箭的推力进而减小第1级耗尽点的动压。

3）提出的优化算法对于初值选择的敏感度较小，具有较强的鲁棒性，且收敛速度较快，方便于进行快速的两级MAV设计优化。

本文仅考虑了总发射质量最小和燃耗最优作为性能指标的火星表面上升段轨迹设计问题，而在实际应用中还需要考虑飞行时间、火星轨道器观测跟踪范围等其他因素，未来需要针对MAV上升轨迹的多性能指标优化开展进一步的研究。