基于约束可满足的深空探测任务规划方法研究

姜啸，徐瑞，朱圣英

（1. 北京理工大学 深空探测技术研究所，北京 100081；2. 深空自主导航与控制工业和信息化部重点实验室，北京 100081）

0 引 言

近年来，约束处理技术成为深空探测自主任务规划研究的热点。关于约束处理技术的应用集中在对约束可满足问题（Constraint Satisfaction Problem，CSP）结构的编码和扩展，以迎合规划领域丰富的表现形式，包括：时间线[1]、概率性[2]、数据流[3]等。美国国家航空航天局（National Aeronautics and Space Administration，NASA）、美国国防部（Department of Defense，DOD）、欧洲航天局（European Space Agency，ESA）等很多机构在规划中引入了CSP技术以支持深空探测器的自主运行，完成复杂的任务目标，具体项目计划包括美国的深空探测计划、基于空间的观测系统（如哈勃太空望远镜）以及ESA的星载自主计划（Project for On-Board Autonomy，PROBA）等。

NASA的深空航天器“深空1号”上使用了RA（Remote Agent）自主控制系统，RA是第1个在任务过程中对航天器进行自主闭环控制的软件[4]。它的规划调度系统RAX-PS采用域描述语言DDL[5]描述结构、功能、资源和各种约束条件等。规划引擎采用各种约束传播算法产生约束网络，通过行径没有解决的冲突并使约束网络一致解决冲突，直到完成任务目标为止。规划过程中采用启发式函数加快求解过程。TechSat21星座中的卫星及EO1航天器上使用了ASE（Autonomous Sciencecraft Experiment）[6]软件，它的决策模块连续活动调度规划执行和重规划系统（Continuous Activity Scheduling Planning Execution and Replanning System，CASPER）使用了局部约束处理技术进行模型的求解，可进行动态连续规划，但规划中只能产生下一个飞行周期的操作计划，不能通过全局约束及时地对实时反馈做出反应。自主规划和调度环境（Autonomous Planning and Scheduling Environment，ASPEN）[7-8]结合宇航器操作约束、飞行规范约束、宇航器硬件模型、科学实验目标和操作过程来自动生成较低层次的宇航器操作序列，NASA已经将其广泛应用在进行外太空任务的宇航器上，包括Citizen Explorer、MARS-1和DS-T等一系列宇航器。NASA实现的可扩展标准化远程操作规划框架（Extensible Unification Remote Operation Planning Framework，EUROPA)[9-10]，以基于约束区间的框架描述调度问题，以基于随机搜索的贪婪算法求解，并考虑了观测任务的优先级。

国内针对基于约束可满足的规划问题研究和国际上仍存在有很大差距，国内主要集中在部分功能约束的规划研究。仲维国研究了星载设备经受动态环境的多种几何和动力学约束时，航天器姿态机动历程的星上规划方法，将姿态路径的规划问题转化为中间节点的规划[11]。程小军、崔祜涛等分析了航天器姿态机动所受的几何约束，设计了保守型的几何约束表达形式[12]。陈德相、徐瑞等针对航天器自主任务规划中的资源受限、约束复杂、活动并行等问题，提出了基于时间拓扑排序的航天器资源处理方法，该方法对资源约束网络的资源突变时刻进行处理，优化了流量推进路径的选择过程[13]。伍丽华、姜云飞等提出一种对时态信息进行表示与管理并且能够进行时态约束推理的一致性赋值方法，使时态推理技术能够更好地应用于时态规划的求解过程中[14]。徐文明、杜智远等提出了可重复的资源约束在规划执行时的可分配处理方法，以及判断资源变量是否满足的可分配性条件[15]。赵凡宇、徐瑞等针对深空探测器的任务规划过程特点，考虑约束的数值特性，提出一种基于规划活动相关度的领域无关启发式规划方法[16]。

现有的研究成果中仅有少量工作涉及到CSP的算法移植性研究，即如何对CSP中标准算法进行重构以适应规划时态搜索特点。CSP中标准的启发式设计并不能很好的利用规划信息引导搜索过程，这在一定程度上降低了搜索的效率。针对该问题，Judge M.、Long D.等[17]给出了基于目标指向的CSP启发式策略。但当问题规模增大时解的长度也随之增加，这将很大程度上降低目标指向约束的约束能力。

本文提出了一种以动作约束为核心的CSP启发式搜索策略。该方法将任务规划中的关键元素映射到CSP中，并以规划中的动作关系为基础，研究并揭示了多层变量CSP中相邻变量的关系，据此提出了CSP中一般性动作约束。该方法避免了当问题规模增大时约束能力衰减的问题。仿真实验表明基于动作约束的扩展GAC与标准一般弧一致（General Arc Consistent，GAC）算法相比具有更好的性能。

2 问题描述

任务规划是关于动作的推理，指的是通过领域中动作的期望效果，选择和组织一组动作，其目的是尽可能好地实现一些预先给定的目标。约束可满足问题由一个变量集合和一个约束集合组成。问题的解是满足所有约束的完全赋值，或更进一步，使目标函数最大化。本节首先对CSP和规划进行了定义说明。

定义1（CSP）一个约束可满足问题由以下几部分组成：

1）变量集X，其中：

2）值域集D，其中：对于X中的任意变量，在D中具有对应的值域；

约束可满足问题的目标是使每一个变量都得到一个赋值，且所有的约束都得到满足。

定义2（任务规划）一个任务规划问题可以表示为一个三元组Q为

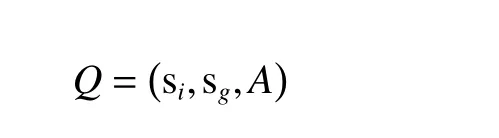
其中：si表示规划系统的初始状态；sg表示规划系统的目标状态；A为规划系统中所有可执行操作的集合。

一般而言，操作集合表示规划中可执行的各种动作，任意动作由二元组组成，其中：pre代表支持动作执行的前提条件，eff代表动作执行后产生的后续状态。

在任务规划与CSP的所有差异之中，关键在于任务规划是一个动态未知的问题。具体而言，在规划前决策者并不知道需要多少个动作支持规划的完成，规划的长度是未知量。而CSP是一个相对静态的问题，在约束处理过程中待求解的变量数目是可见的，换言之，CSP的长度是可知的。为了能够将CSP技术应用于规划问题，Kautz与Selman提出了针对规划问题的定界分层方法，为基于约束可满足的自主规划技术奠定了理论基础。该方法在规划前对解的长度进行预估，例如假设该规划问题可用k个动作完成，便定义CSP模型具有k层结构，每层均是变量集和约束集的一个副本。若CSP在k层中无解，对k值迭代增加，直到获得可行解。该方法将NP难的规划问题通过长度限定降为一个NP问题，从而可以通过CSP求解这种NPC问题获得可行解。

基于定界分层方法，对于编码为CSP的规划问题本文从变量、约束和算法3个方面进行如下设计。

1）变量

假定任意规划问题具有m多值状态变量，对于规划中任意层0 ≤≤n中每个状态变量Vi，在对应的CSP结构中均包含对应的变量V，其值域与Vi的值域一一对应。因此，在该CSP中包含m（n+ 1）个变量。

2）约束

本文主要包含涉及规划领域信息的4条约束：初始状态约束、目标状态约束、动作的前提条件约束以及动作的效果约束。初始状态约束限定了CSP中变量在初始层的取值范围（k= 0），目标状态约束限定了CSP中目标层变量的取值范围。任务规划中的动作关系转化为前提条件约束和效果约束。例如，动作photo限定了探测器对某目标进行拍照。若该动作在i层执行，前提条件约束限定了photo的前提条件point-to必须于i层之前发生，保证在拍摄前探测器指向目标。

3）算法

本文采用一般弧一致GAC算法[18]作为算法框架，并在此基础上对其变量选择的启发式进行改进。GAC算法的核心是检查每个未赋值变量的值域，并剪枝不符合约束的取值。如果剪枝操作导致该变量值域为空，则算法进行回溯。GAC对CSP中的约束进行弧一致的检查也采用上述策略：GAC首先检查当前约束中未赋值的变量并对其值域进行剪枝，当该变量值域剪枝至空时将所有包含该变量的约束加入GAC算法待扩展的约束列表中。

3 动作约束分析

当CSP问题规模增大时，初始状态约束以及目标状态约束对整个CSP的约束能力将逐步减小。因此，本文主要对贯穿整个CSP的动作约束进行考察。

在规划领域，动作的前提条件与后续状态规则如下：

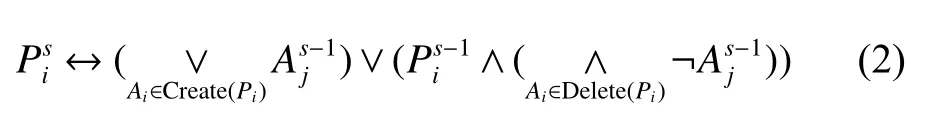
在CSP中动作常常转化为约束的形式，并不能显式存在于问题处理过程之中，所以将规划领域中的关键元素映射到CSP领域使之能够符合CSP算法的处理过程十分必要。例如，符号及在规划领域代表某一动作的真值，而对应的CSP领域中代表该动作约束是否具有一致性。为了避免混淆，下文中如非特指A均代表CSP中的动作约束。从规划至CSP的映射关系为

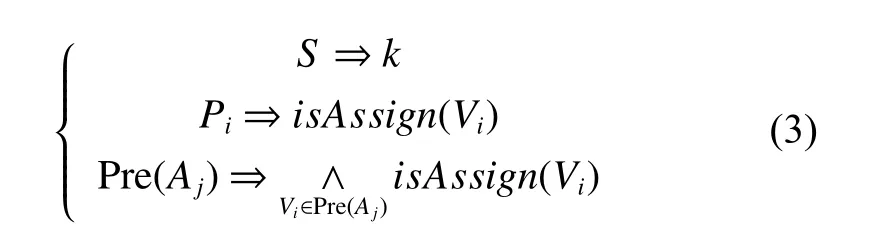
在规划中，动作的前提条件表现为处于某种特殊状态的实体。例如假定动作pickup的前提为：球在地上；手是空的。则该动作的前提条件表示为显然在CSP中{ball，hand}可表示为变量，{ground，empty}为对应的值域。广而言之，规划中某状态为真，CSP表示为对应变量的赋值，符号定义为：动作的前提条件可表示为所有支持变量赋值的交集，符号定义为

为了阐述清晰，进行如下两个定义：

定义3（前件动作约束：preaction constraints）

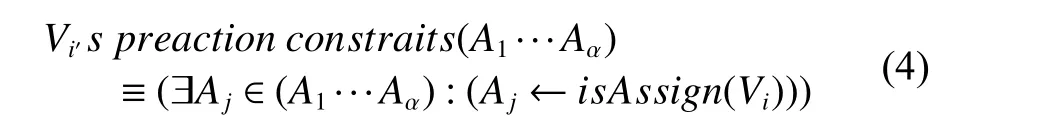
定义4（前件状态变量：precondition variables）支持动作约束一致的全体变量集，称为的前件状态变量。符号定义为

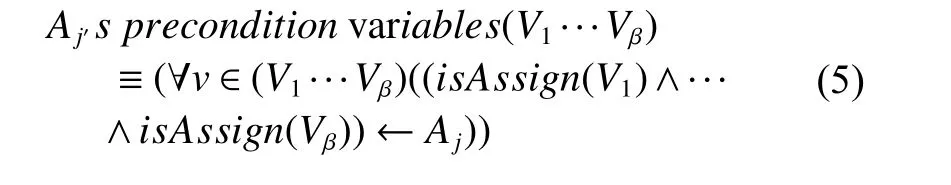
根据规划中的动作后续状态关系，式（2）由2部分组成。第1部分代表了存在动作使在s－1为真，体现规划中实例化的操作。第2部分代表在以前的状态中为真同时没有动作使之为假，体现了规划过程的连续性。然而，由于CSP是一个静态的问题。在多层变量的结构中发现不同层之间并不存在连续性，每一层变量都需要独立赋值。式（2）转化为CSP结构后只需考察第一部分即可，对应的转换公式为

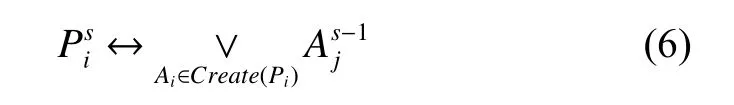
根据式（1）～（6），可推导CSP中的动作约束关系为

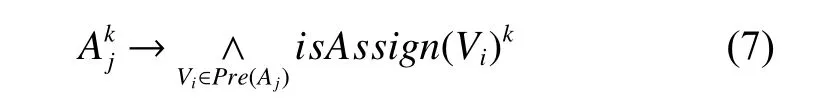
CSP中的继承状态关系为

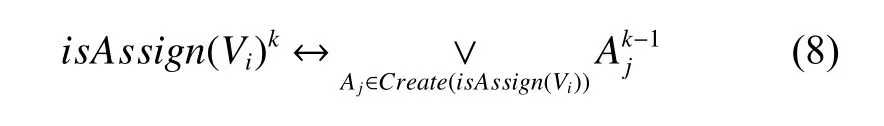
由于在CSP中动作表示为约束形式，并不在赋值操作中显式表示，因此联立式（7）～（8）进一步推导为

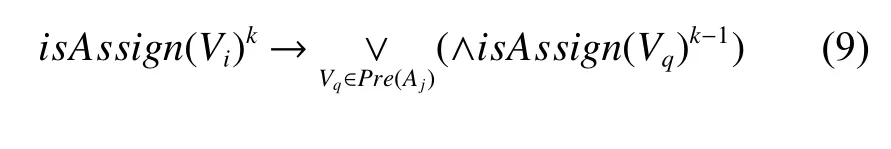
或表示为否定形式

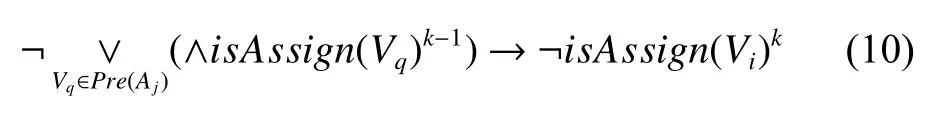
式（9）～（10）揭示了相邻层变量的赋值关系：在k层的变量Vi能够赋值，仅当在k– 1层中，包含Vi的前件动作约束的前件状态变量已被赋值。

基于以上结论以及安全性考虑，根据相邻变量关系提出了变量继承约束：

变量继承约束：k层变量能够赋值仅当k– 1层中全部变量已完成赋值。符号表示如下

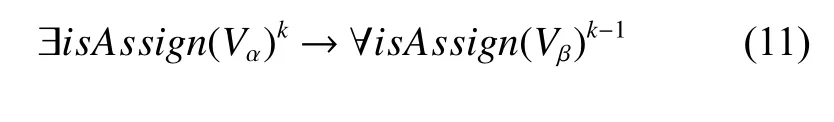
4 基于变量继承约束的算法设计

本文基于GAC算法框架并加入约束（11）进行改进，改进后的算法伪代码图1所示。

图1 扩展GAC算法伪代码Fig. 1 Pseudo code for extended GAC algorithm

在变量选择环节，算法首先记录每个变量涉及到的约束数目，该数据用于对相同启发值的候选解做进一步的区分。接下来算法从层数为1开始挑选变量。在该环节中，采用了动态变量排序以及最大约束变量启发式技术。在当前层中的变量都完成赋值后，算法将扩展至下一层，并重复上述过程。

算法中改进式的变量挑选方法优势包括：

1）该约束对于所有约束可满足编码的规划问题具有一般性。

本文提出的变量继承约束是由式（9）～（10）推导出的，在式（9）～（10）的推导过程中其理论基础来源于规划领域的动作前件/后件关系以及CSP编码的多层变量框架。变量继承约束为规划领域基础的逻辑关系，后者为所有CSP编码规划问题均采用的框架结构，因此式（11）对于所有的CSP编码规划问题都具有一般性。

2）该约束下的变量选择方法具有更好的时间复杂度。

改进GAC算法根据约束式（11）挑选出候选变量，鉴于约束式（11）基于动作逻辑关系推导，因此该候选变量在约束传播过程中不会再次违反规划的动作逻辑关系。这极大减少了潜在的回溯次数，降低了无效的约束检查次数。

3）该约束能够降低算法中无效的约束检查次数。

5 仿真实验

本文的实验环境为微软Visual Studio开发环境，Intel 3.5 GHz CPU，1 GB RAM。测试算例采用国际规划大赛（International Planning Competitions，IPC）经典算例，测试算法的一般性以及深空探测器观测数传事件测试算法的实用性。测试应用的IPC算例包括：BlockWorld，Grid，Gripper，Logistics以及Mystery。

表1展示了对IPC算例测试中GAC与其扩展算法约束检查数目的对比。在测试的5个算例中，扩展算法均降低了约束检查的数目，在某些算例中尤为明显。例如，在Grid算例中，为解决该规划问题GAC算法需进行39 214 667次约束检查；而包含动作约束的改进GAC算法仅需要6 527 187次。

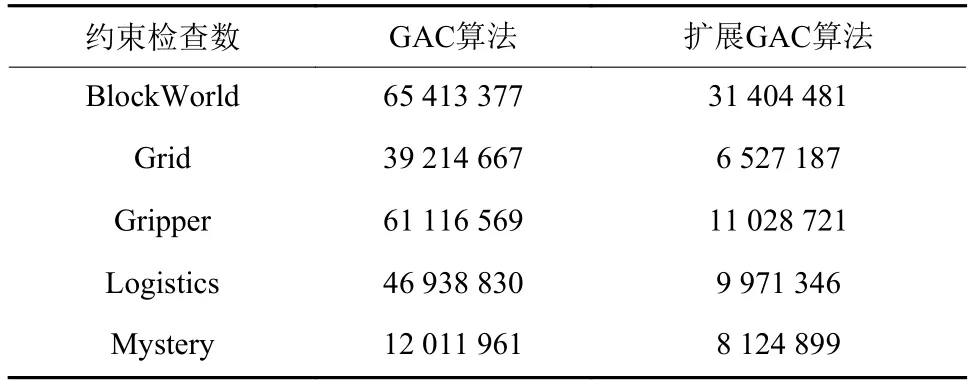
表1 约束检查数目对比Table 1 Comparison of number of constraint checks

由于动作约束的引导，扩展GAC算法能够“避开”大量的无效约束检查操作，因此问题求解效率也得到极大提高。表2展示了求解IPC算例的平均时间对比，由于扩展GAC有着更高效的变量选取已经回避了大量的无效约束检查，其求解效率远高于标准GAC算法。

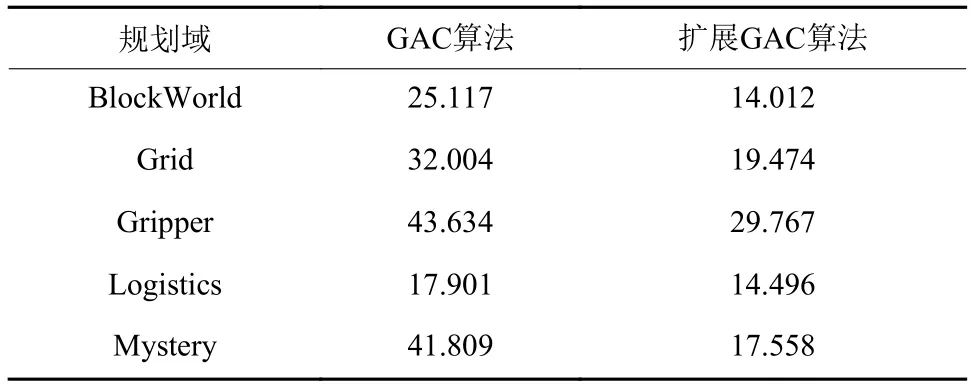
表2 搜索时间对比Table 2 Comparison time for Gripper domain s

图2以Gripper领域为例展示了标准GAC算法与本文提出的基于变量继承约束的扩展GAC算法在问题规模逐步扩大情况下CPU运行时间的对比。图中表明随着问题规模变大，扩展GAC算法能够在动作约束中获得更大的收益，其规划时间的增长速度远小于GAC算法的增长速度。

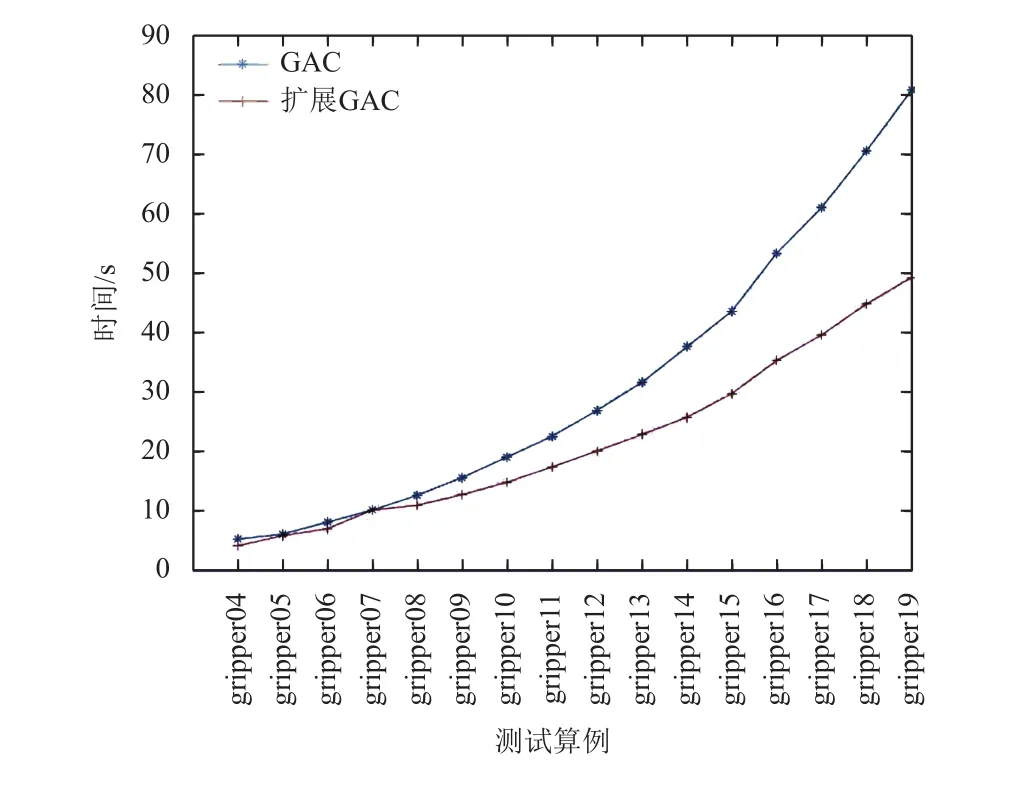
图2 Gripper领域时间对比Fig. 2 Comparison time for Gripper domain

不仅如此，大量的冗余计算将占用计算设备大量的存储空间。随着问题规模逐步扩大，将导致问题求解的失败。例如，GAC算法仅能求解Mystery领域的前3个算例，当Mystery问题规模变大时，GAC将无法得到规划解。而扩展GAC由于减少了大量的冗余计算，其求解结果如图3所示。

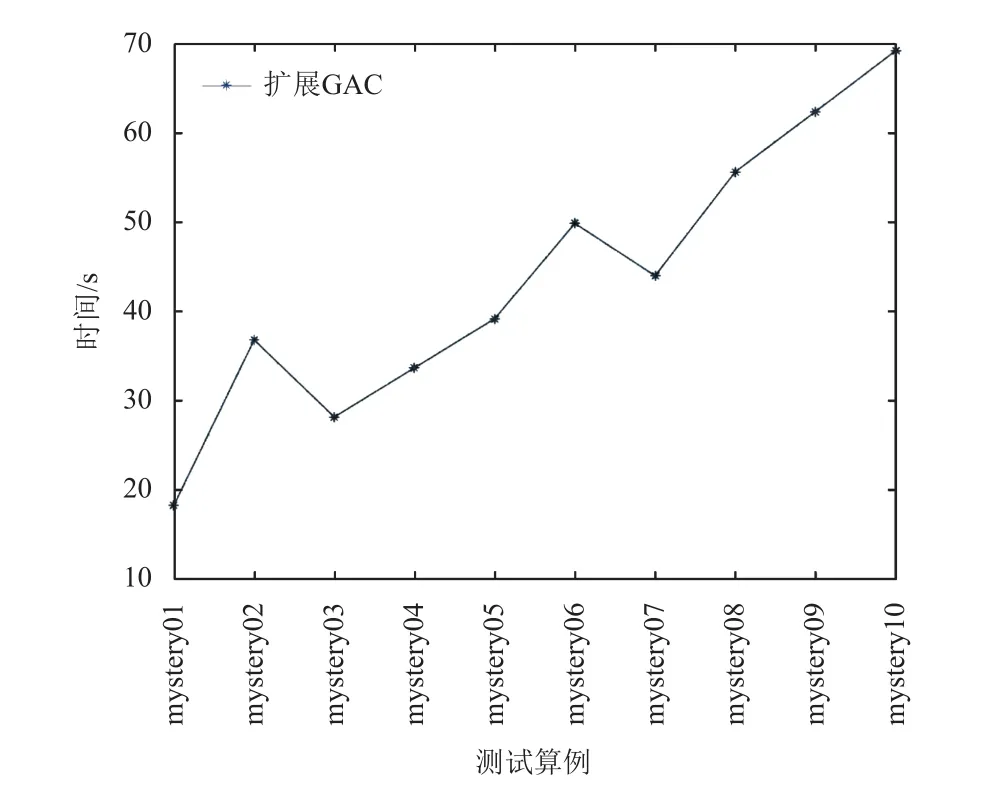
图3 扩展GAC在Mystery域的搜索时间Fig. 3 Search time of extended GAC algorithm in Mystery domain

在对算法工程适用性的考察中，本文选取了深空探测活动中典型的对目标拍照并对地数传事件，忽略上传动作的简化MEX模型[19]。该模型为2012年国际知识工程规划调度大赛模型中基于火星快车任务的算例，涉及到地面站、观测器、内存、温控器以及姿控系统等多种活动单元，各单元涉及到的动作如表3所示。

表3 拍照数传算例的变量及活动Table 3 The variables and activities for the example of taking photos

针对拍照数传活动本文根据不同数目的子系统进行了10组仿真测试，子系统的数量以及目标数随算例逐渐增加，每组的算例如表4所示。例如算例4表示探测器存在4个目标需要拍照，探测器上携带2个相机，2个内存用于存储数据，2个对应的温控装置用于调节相机的温度，以及一个地面站接受数据。10组仿真测试结果如图4所示，可以看到扩展GAC求解问题的时间均少于GAC算法。

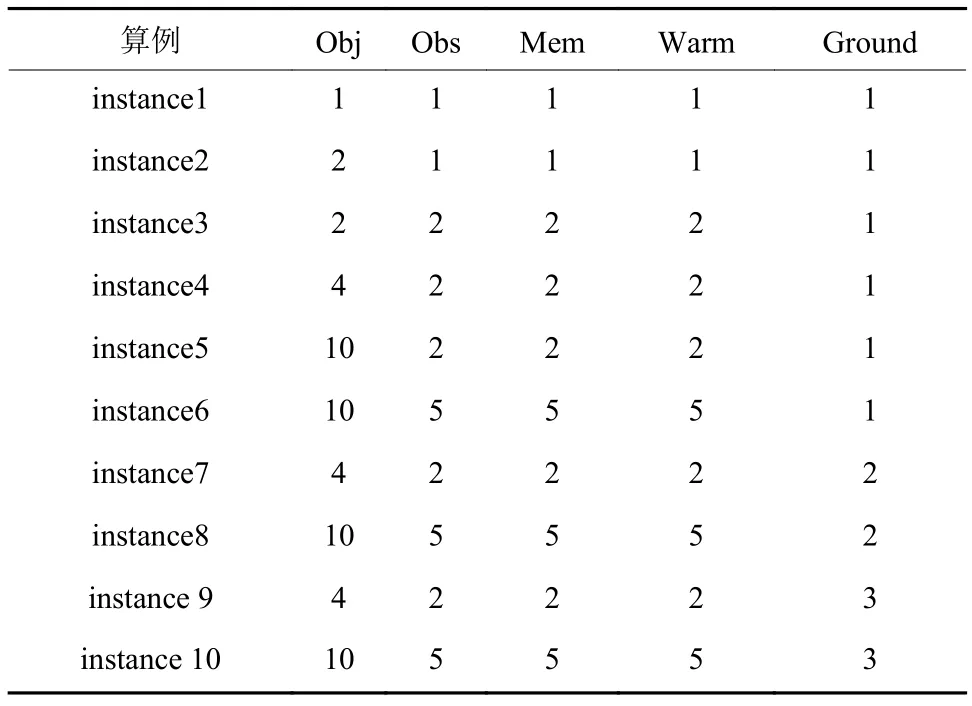
表4 10组拍照数传算例展示Table 4 The test instances of ten taking photos

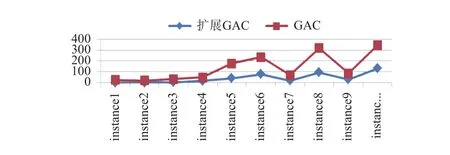
图4 拍照数传算例时间对比Fig. 4 Time comparison of the example of taking photos

6 结 论

本文提出了一种以动作为中心的约束可满足技术用于深空探测规划问题。研究表明，通过充分利用任务规划的特点改进标准约束可满足算法可以获得较好的效率。通过将任务规划问题中的动作关系映射到CSP中，揭示了多层变量CSP结构中相邻层间变量的关系。在此基础上提出的动作约束使得CSP中的变量选择更为合理，能够有效地减少变量选择的时间消耗以及无效的约束检查数。理论分析表明，该方法适用于一般的约束规划问题。仿真实验验证了基于动作约束的扩展GAC与标准GAC算法相比具有更好的性能，未来可应用到工程实践中。