双星系统L1点悬停探测控制器设计与仿真

张永隆，刘华缨，曾祥远

（北京理工大学 自动化学院，北京 100081）

0 引 言

双星系统作为一种特殊的小天体系统，是当前深空探测领域的研究热点。科学家们发现人类所观测到的直径大于200 m的近地小行星中约有16%可能属于双星系统[1]。自1996年美国发射人类历史上第一颗小行星探测器NEAR开始，美国、日本、欧洲等国家曾多次发射单个小天体探测器，我国也于2010年发射“嫦娥2号”探测器，飞越探测了小行星4179 Toutatis。除了美国在1989年发射的木星探测器“伽利略号”在飞行过程中偶遇243 Ida小行星，并第一次发现其为双星系统外[2]，人类目前尚未对双星系统进行较为实质性的探测。值得关注的是，美国航空航天局（National Aeronautics and Space Administration，NASA）和欧洲空间局（European Space Agency，ESA）正在合作开展人类历史上第一次真正意义上的双星探测任务，即“小行星碰撞和偏移评估任务”（Asteroid Impact & Deflection Assessment，AIDA），该任务计划将于2019年发射2颗航天器到Didymos双星系统，一颗负责撞击次星，另一颗负责观测[3]。

双星系统悬停探测是指探测器在双星系统附近与双星系统保持空间相对位置不变进行探测。由于小天体外形复杂，在对小天体进行撞击、着陆等任务之前，对其进行悬停探测是必要的。在悬停过程中，对小天体开展进一步精确观测，以便进行后续任务操作。从理论上讲，在系统平动点处，忽略其他摄动力的情况下探测器所受引力与离心力相互抵消，合力为零，因此悬停探测常选取系统平动点作为悬停位置。对于双星系统而言，由于L1点位于双星之间，在L1点悬停可以同时观测主星与次星，因此双星系统L1点悬停探测具有更高的工程应用价值。

解决双星系统L1点悬停控制问题大致可分为两个步骤：引力场建模及平动点求解和控制器设计。双星系统作为一类特殊的小天体系统，引力场建模可以采用多面体法、级数展开法、质点群法以及简化模型法[4]等小天体常用引力场建模方法[5-7]。Furfaro针对椭球体单个小行星悬停控制设计了高阶滑模控制器[8]，Yang等针对多面体模型下的单个小行星悬停控制设计了终端滑模控制器[9]，Zeng等分析了太阳帆航天器本体系悬停探测细长形小行星的可行性[10-11]，Bu等研究了连续小推力下双星系统人工平动点的位置和动力学特性[12]，但目前尚未见到双星系统悬停探测控制器设计的相关研究。

本文第1节利用球谐函数展开法对双星系统进行引力场建模，将双星系统引力场展开至二阶二次势函数。针对双星系统L1点悬停控制设计了一种原理简单、便于工程实现的bang-bang控制器；第2节选取Hermes双星系统作为仿真算例，验证所设计控制器的有效性；第3节总结全文。

1 双星系统L1点悬停控制数学模型

图1所示为双星系统及其参考坐标系：坐标系以双星系统质心为坐标原点，x轴正方向由次星指向主星，z轴方向为系统角动量方向，y轴与x轴和z轴构成右手直角坐标系。lL为探测器相对于质心的位置矢量rL表示次星到主星之间的位置矢量。μ=M1/（M1+M2）为系统的质量比。

图1 双星系统示意图与参考坐标系Fig. 1 Schematic map of the body-fixed frame of the binary asteroid system

本文研究中椭球引力场建模截取至二阶二次势函数，以次星椭球体M2中的最长轴半径a2和系统的平均角速度分别作为系统长度与角速度归一化单位。采用归一化单位制后，r=rL/a2，l=lL/a2= [x，y，z]T。其用椭球体模型计算得出椭球体M1和椭球体M2的势函数为

椭球体的三轴转动惯量为

球谐系数与椭球3个主轴惯量的关系为[13-16]

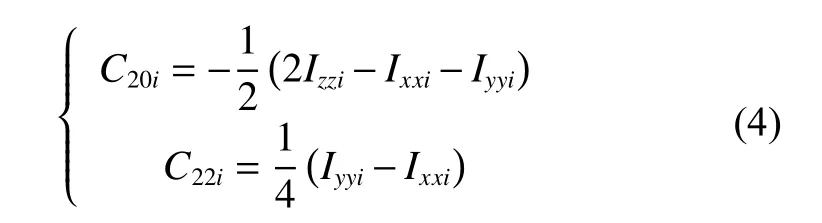
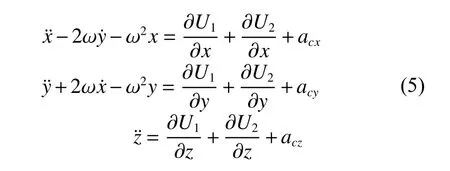
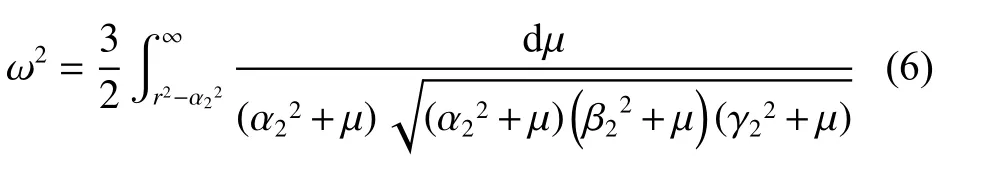
设L1点坐标为为位置误差矢量。考虑到探测器发动机现阶段多为采用bang-bang脉冲推力式发动机，本文采用常值切换控制策略为

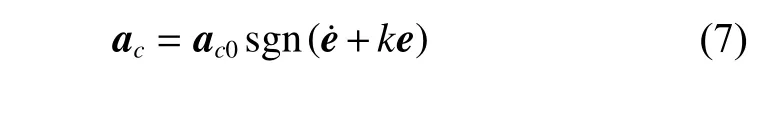
其中：ac0为探测器发动机所提供控制加速度。

2 仿真算例

本文以Hermes双星系统为例进行仿真计算，Hermes双星系统主星可看作三轴半径分别为315 m、308.7 m、302.4 m椭球体，次星可看作三轴半径分别为280 m、271.6 m、268.8 m椭球体。双星系统质量比为μ= 0.595 2，两星距离rL= 1 200 m[18]，由此求得Hermes系统5个平动点，其位置（归一化单位制下）如图2所示。

图2 Hermes双星系统5个平动点Fig. 2 The sketch of binary asteroid Hermes and its equilibrium points

图3 位置误差变化曲线Fig. 3 Normalized relative position errors in three axes

图4 速度误差曲线Fig. 4 Normalized relative velocitie errors in three axes

图5 控制加速度曲线Fig. 5 Normalized control accelerations in three axes

在式（7）中，由于控制器参数k只要求为任意正数，因此在上述仿真过程中将k初步给定为1。然而k的取值不同却会影响控制效果，所以可以通过对控制器参数k进行优化，从而进一步改善控制器性能，缩短收敛时间。

设置时间从0～100 s，幅值恒为0的信号为参考目标信号，令三轴位置误差信号跟踪该参考目标信号，使用遗传算法对控制器参数k进行优化，优化后k=0.320 3。利用此优化后的控制器参数再次进行相同仿真，得到其三轴位置误差、速度误差与控制加速度变化曲线分别如图6～9所示，其中各坐标轴单位均与图3～5相同。由图6～7可知，参数k优化后，不仅保持x轴与y轴位置和速度误差在20 s内收敛到零，z轴位置和速度误差也在20 s左右收敛到零，且三轴位置曲线超调量均明显小于图3中曲线超调量，控制效果明显得到改善。

在图8控制律作用下，探测器转移轨迹如图9所示，可以看出，探测器成功从初始位置受控飞行到目标位置L1点。

图6 优化后位置误差变化曲线Fig. 6 Normalized relative position errors in three axes

图7 优化后速度误差曲线Fig. 7 Normalized relative velocitie errors in three axes

图8 控制加速度曲线Fig. 8 Normalized control accelerations in three axes

图9 探测器至L1点转移轨迹Fig. 9 The transfer trajectory for the spacecraft flying to L1

3 结 论

利用球谐函数法对双星系统引力场进行建模，针对航天器在双星系统L1点悬停飞行设计了一种常值切换bang-bang控制器。以双星系统Hermes为例开展了仿真研究，20 s左右三轴位置误差均收敛至零，验证了控制器的有效性。更多关于双星系统悬停探测的控制器设计与改进留作后续研究。